Article contents
The completeness of the first-order functional calculus
Published online by Cambridge University Press: 12 March 2014
Extract
Although several proofs have been published showing the completeness of the propositional calculus (cf. Quine (1)), for the first-order functional calculus only the original completeness proof of Gödel (2) and a variant due to Hilbert and Bernays have appeared. Aside from novelty and the fact that it requires less formal development of the system from the axioms, the new method of proof which is the subject of this paper possesses two advantages. In the first place an important property of formal systems which is associated with completeness can now be generalized to systems containing a non-denumerable infinity of primitive symbols. While this is not of especial interest when formal systems are considered as logics—i.e., as means for analyzing the structure of languages—it leads to interesting applications in the field of abstract algebra. In the second place the proof suggests a new approach to the problem of completeness for functional calculi of higher order. Both of these matters will be taken up in future papers.
The system with which we shall deal here will contain as primitive symbols
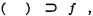
and certain sets of symbols as follows:
(i) propositional symbols (some of which may be classed as variables, others as constants), and among which the symbol “f” above is to be included as a constant;
(ii) for each number n = 1, 2, … a set of functional symbols of degree n (which again may be separated into variables and constants); and
(iii) individual symbols among which variables must be distinguished from constants. The set of variables must be infinite.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1949
References
BIBLIOGRAPHY
- 271
- Cited by


