Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T06:01:42.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Completeness of MLL proof-nets w.r.t. weak distributivity

Published online by Cambridge University Press:  12 March 2014

Jean-Baptiste Joinet
Jean-Baptiste Joinet*
Affiliation:
EQUIPE Preuves-Programmes-SystÈmes, CNRS - UniversitÉ, Paris 7 (UMR 7126), Case 7014, 2 Place Jussieu, F-75251 Paris Cedex 05, France. E-mail: joinet@pps.jussieu.fr URL: www-philo.univ-parisl.fr/Joinet
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine ‘weak-distributivity’ as a rewriting rule 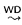defined on multiplicative proofstructures (so, in particular, on multiplicative proof-nets: MLL). This rewriting does not preserve the type of proof-nets, but does nevertheless preserve their correctness. The specific contribution of this paper, is to give a direct proof of completeness for 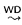: starting from a set of simple generators (proof-nets which are a n-ary ⊗ of Ց-ized axioms), any mono-conclusion MLL proof-net can be reached by 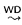rewriting (up to ⊗ and Ց associativity and commutativity).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 1 , March 2007 , pp. 159 - 170
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bechet, D., de Groote, P., and Retoré, C., A complete axiomatisation for the inclusion of seriesparallel orders, RTA 97, Lecture Notes in Computer Science, vol. 1232, 1997, pp. 230–240.Google Scholar
[2]Danos, V., La logique linéaire appliquée à l'etude de divers processus de normalisation (principalement du λ-calcul), Ph.D. thesis, Université Paris 7, 06 1990.Google Scholar
[3]Danos, V., Joinet, J-B., and Schellinx, H., Computational isomorphisms in classical logic, Theoretical Computer Science, vol. 294 (2003), no. 3, pp. 353–378.CrossRefGoogle Scholar
[4]Danos, V. and Regnier, L., The structure of multiplicatives, Archives for Mathematical Logic, vol. 28 (1995), pp. 181–203.Google Scholar
[5]Devarajan, H., Hughes, D., Plotkin, G., and Pratt, V., Full completeness of the multiplicative linear logic of Chu spaces, Proceedings 14th Annual IEEE Symposium on Logic in Computer Science, LICS '99 (Longo, G., editor), 1999, pp. 234–242.Google Scholar
[6]Girard, J.-Y., Linear logic. Theoretical Computer Science, vol. 50 (1987), pp. 1–102.CrossRefGoogle Scholar
[7]Guglielmi, A., A system of interaction and structure, Technical Report WV-02-10, International Center for Computational Logic, Technische Universität Dresden, Germany, 8 November 2004, To appear on ACM Transactions on Computational Logic.Google Scholar
[8]Maieli, R. and Puite, Q., Modularity of proof nets: generating the type of a module, Archive for Mathematical Logic, vol. 44 (2005), no. 2, pp. 167–193.CrossRefGoogle Scholar
[9]Retoré, C., Handsome proof-nets: R&B graphs, perfect matchings and Series-Parallel graphs, Technical Report RR-36-52, INRIA, 1999.Google Scholar