Article contents
Categoricity and U-rank in excellent classes
Published online by Cambridge University Press: 12 March 2014
Abstract
Let 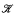 be the class of atomic models of a countable first order theory. We prove that if
be the class of atomic models of a countable first order theory. We prove that if 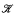 is excellent and categorical in some uncountable cardinal, then each model is prime and minimal over the basis of a definable pregeometry given by a quasiminimal set. This implies that
is excellent and categorical in some uncountable cardinal, then each model is prime and minimal over the basis of a definable pregeometry given by a quasiminimal set. This implies that 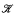 is categorical in all uncountable cardinals. We also introduce a U-rank to measure the complexity of complete types over models. We prove that the U-rank has the usual additivity properties, that quasiminimal types have U-rank 1, and that the U-rank of any type is finite in the uncountably categorical, excellent case. However, in contrast to the first order case, the supremum of the U-rank over all types may be ω (and is not achieved). We illustrate the theory with the example of free groups, and Zilber's pseudo analytic structures.
is categorical in all uncountable cardinals. We also introduce a U-rank to measure the complexity of complete types over models. We prove that the U-rank has the usual additivity properties, that quasiminimal types have U-rank 1, and that the U-rank of any type is finite in the uncountably categorical, excellent case. However, in contrast to the first order case, the supremum of the U-rank over all types may be ω (and is not achieved). We illustrate the theory with the example of free groups, and Zilber's pseudo analytic structures.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2003
References
REFERENCES
- 4
- Cited by


