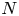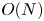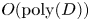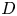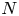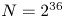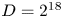1. Introduction
The term ‘quantum-inspired algorithms’ loosely describes a set of classical algorithms that use some concepts from their quantum counterparts. They often obtain comparable speed-ups so long as some error with respect to the true solution can be tolerated and the original problem of interest has some (potentially unknown) underlying structure that can be capitalized upon. In the context of solving partial differential equations (PDEs), quantum-inspired algorithms use a quantum-like representation of the classical dataset. One can then use classical methods for quantum simulation to approximately solve the PDE. One natural choice is the tensor network framework, a popular tool in the quantum chemistry and condensed matter communities (White Reference White1993; Chan & Head-Gordon Reference Chan and Head-Gordon2002; Vidal Reference Vidal2003; White Reference White2005; Schollwöck Reference Schollwöck2011) since it may allow for efficient representation and manipulation of the quantum-like dataset, so long as the dataset is low rank.
This concept was first introduced several years ago and is referred to as quantics or quantized tensor trains (QTTs) because the data are artificially folded into a high-dimensional tensor representing many small ‘quants’ of data (Oseledets Reference Oseledets2009, Reference Oseledets2010; Khoromskij Reference Khoromskij2011; Dolgov, Khoromskij & Oseledets Reference Dolgov, Khoromskij and Oseledets2012). (Tensor trains are tensor networks with a one-dimensional (1-D) geometry.) It was also proven that several 1-D functions (exponential, trigonometric, polynomial) and common operators (e.g. differential operators) on a uniform grid can be efficiently represented in the QTT format (Khoromskij Reference Khoromskij2011; Kazeev & Khoromskij Reference Kazeev and Khoromskij2012; Kazeev, Reichmann & Schwab Reference Kazeev, Reichmann and Schwab2013b). It follows that one can often obtain a loose bound on the QTT rank for other smooth functions by expanding them in terms of exponential or polynomial basis sets (Dolgov et al. Reference Dolgov, Khoromskij and Oseledets2012), though tighter bounds can be obtained (Lindsey Reference Lindsey2023). However, non-smooth functions can have efficient representations too; the Heaviside step function can be represented with just rank two, triangle functions with rank three (Gourianov et al. Reference Gourianov, Lubasch, Dolgov, van den Berg, Babaee, Givi, Kiffner and Jaksch2022). The underlying intuition is that functions with some degree of scale locality, meaning that features on long length scales are relatively independent of behaviour at small length scales, can be represented as a tensor network with low rank. Since it is believed that turbulent systems also exhibit some degree of scale locality, tensor networks may even be able to efficiently capture turbulent dynamics (Gourianov Reference Gourianov2022).
Several recent works solve the Navier–Stokes equations using the QTT format (Gourianov et al. Reference Gourianov, Lubasch, Dolgov, van den Berg, Babaee, Givi, Kiffner and Jaksch2022; Kiffner & Jaksch Reference Kiffner and Jaksch2023; Kornev et al. Reference Kornev, Dolgov, Pinto, Pflitsch, Perelshtein and Melnikov2023; Peddinti et al. Reference Peddinti, Pisoni, Marini, Lott, Argentieri, Tiunov and Aolita2023) with reasonable success. In this work, we aim to solve the Vlasov equation, a ($6+1$![]() )-dimensional PDE that provides an ab initio description of collisionless plasma dynamics in the presence of self-consistent electromagnetic fields computed via coupling to Maxwell's equations. Being able to perform these calculations would greatly advance our understanding of many astrophysical phenomena and fusion energy systems. However, while the coupled Vlasov–Maxwell system is the gold standard for plasma simulation, its use is limited due to prohibitively high computational costs.
)-dimensional PDE that provides an ab initio description of collisionless plasma dynamics in the presence of self-consistent electromagnetic fields computed via coupling to Maxwell's equations. Being able to perform these calculations would greatly advance our understanding of many astrophysical phenomena and fusion energy systems. However, while the coupled Vlasov–Maxwell system is the gold standard for plasma simulation, its use is limited due to prohibitively high computational costs.
There is a class of low-rank grid-based solvers that are closely related to the proposed QTN solver, except that only low-rank approximations with respect to physical dimensions (i.e. the spatial and velocity coordinates) are considered (Kormann Reference Kormann2015; Einkemmer & Lubich Reference Einkemmer and Lubich2018; Allmann-Rahn, Grauer & Kormann Reference Allmann-Rahn, Grauer and Kormann2022; Einkemmer Reference Einkemmer2023). These studies show that, often, only modest rank is required to perform common test problems with sufficient accuracy, leading to significant reduction in computational cost. While the mechanics of these solvers are similar to what will be discussed here, they are fundamentally different in that they are not quantized and low-rank approximations within each dimension cannot be made.
Prior work on solving the Vlasov equation with QTTs assumed electrostatic fields, and only considered calculations with one axis in real space and one axis in velocity space (1D1V) (Ye & Loureiro Reference Ye and Loureiro2022). Here, we consider higher-dimensional plasmas in 2D3V (though the algorithm can readily be extended to 3D3V calculations) in the presence of electromagnetic fields. We first start with a brief overview of the Vlasov equation and QTTs, and then introduce a comb-like quantized tree tensor network (QTC) geometry that we expect to be a more efficient representation for high-dimensional data than the standard tensor train geometry. In the following section, we detail our semi-implicit finite-difference Vlasov solver in the QTN format. Most notably, we discuss how one can modify the problem such that positivity of the distribution function is preserved despite the low-rank approximation, and introduce a QTN time evolution scheme that allows one to take larger time steps than allowed by traditional grid-based methods. Finally, we close with numerical simulations of the Orszag–Tang vortex and the geospace environmental modelling (GEM) magnetic reconnection problem in 2D3V and a discussion on our observations.
2. Quantized tensor networks
Quantized tensor networks are a multi-scale ansatz built from a set of interconnected high-dimensional matrices typically referred to as tensors (Oseledets Reference Oseledets2009; Khoromskij Reference Khoromskij2011; Dolgov Reference Dolgov2014). For more background information on QTNs, we refer readers to the previous references as well as the papers of Garcia-Ripoll (Reference Garcia-Ripoll2021) and Ye & Loureiro (Reference Ye and Loureiro2022).
Suppose a 1-D function ${h}(x)$![]() is discretized into $N=d^L$
is discretized into $N=d^L$![]() grid points. One can quantize the representation, by which one defines artificial dimensions to describe the function. This effectively appears as reshaping the vector into an $L$
grid points. One can quantize the representation, by which one defines artificial dimensions to describe the function. This effectively appears as reshaping the vector into an $L$![]() -dimensional tensor with size $d$
-dimensional tensor with size $d$![]() along each dimension, $h(x) \cong \textsf{h}(i_1,i_2,\ldots,i_L)$
along each dimension, $h(x) \cong \textsf{h}(i_1,i_2,\ldots,i_L)$![]() , where the indices $i_1, i_2,\ldots i_L \in \{ 0, \ldots, d-1\}$
, where the indices $i_1, i_2,\ldots i_L \in \{ 0, \ldots, d-1\}$![]() encode the grid points in $x$
encode the grid points in $x$![]() . For example, if $d=2$
. For example, if $d=2$![]() , one possible encoding is a binary mapping, such that the $i$
, one possible encoding is a binary mapping, such that the $i$![]() th grid point is indexed by its binary string $(i_1, i_2,\ldots, i_L)_2$
th grid point is indexed by its binary string $(i_1, i_2,\ldots, i_L)_2$![]() . In this case, the indices sequentially correspond to finer grid resolutions. Another possible encoding is a signed register, in which one takes the two's complement of the physical indices conditioned on the first index, such that $i \cong (i_1, i_1 + i_2,\ldots, i_1 + i_L)_2$
. In this case, the indices sequentially correspond to finer grid resolutions. Another possible encoding is a signed register, in which one takes the two's complement of the physical indices conditioned on the first index, such that $i \cong (i_1, i_1 + i_2,\ldots, i_1 + i_L)_2$![]() . This mirror-like mapping may be more efficient for symmetric functions, since the second half of the data is flipped with respect to the original (Garcia-Ripoll Reference Garcia-Ripoll2021). It is used later in § 5 when representing Gaussian functions.
. This mirror-like mapping may be more efficient for symmetric functions, since the second half of the data is flipped with respect to the original (Garcia-Ripoll Reference Garcia-Ripoll2021). It is used later in § 5 when representing Gaussian functions.
To obtain a QTT representation, the $L$![]() -dimensional tensor is decomposed into a 1-D chain of $L$
-dimensional tensor is decomposed into a 1-D chain of $L$![]() tensors:
tensors:

where $\textsf{M}^{(p)}$![]() is the $p$
is the $p$![]() th tensor in the chain with one ‘physical’ bond ($i_p$
th tensor in the chain with one ‘physical’ bond ($i_p$![]() ) of size $d$
) of size $d$![]() that is used to access the actual data, and two ‘virtual’ bonds ($\alpha _{p-1}, \alpha _{p}$
that is used to access the actual data, and two ‘virtual’ bonds ($\alpha _{p-1}, \alpha _{p}$![]() ) of size $r_{p-1}$
) of size $r_{p-1}$![]() and $r_{p}$
and $r_{p}$![]() that connect the tensor to its two neighbours. Upon contraction of the tensor network, the sums in the above equation are performed and the virtual bonds no longer exist. (The exceptions are $\textsf{M}^{(1)}$
that connect the tensor to its two neighbours. Upon contraction of the tensor network, the sums in the above equation are performed and the virtual bonds no longer exist. (The exceptions are $\textsf{M}^{(1)}$![]() , which only has one virtual bond ($\alpha _1$
, which only has one virtual bond ($\alpha _1$![]() ) of size $r_1$
) of size $r_1$![]() , and $\textsf{M}^{(L)}$
, and $\textsf{M}^{(L)}$![]() , which also only has one virtual bond ($\alpha _{L-1}$
, which also only has one virtual bond ($\alpha _{L-1}$![]() ) of size $r_{L-1}$
) of size $r_{L-1}$![]() .) The simplest way to obtain the tensors in (2.1) is to perform a series of singular value decompositions (Oseledets Reference Oseledets2010), isolating each dimension $i_p$
.) The simplest way to obtain the tensors in (2.1) is to perform a series of singular value decompositions (Oseledets Reference Oseledets2010), isolating each dimension $i_p$![]() one at a time. If no approximation is made and the vector is full-rank, then rank $r_p$
one at a time. If no approximation is made and the vector is full-rank, then rank $r_p$![]() is $\min (d^p, d^{L-p})$
is $\min (d^p, d^{L-p})$![]() . The rank is largest at the middle of the tensor train, with $r_{L/2}=d^{L/2}=\sqrt {N}$
. The rank is largest at the middle of the tensor train, with $r_{L/2}=d^{L/2}=\sqrt {N}$![]() . To obtain a good low-rank approximation, one would keep only the $D$
. To obtain a good low-rank approximation, one would keep only the $D$![]() largest singular values at each decomposition step. This parameter is referred to as the bond dimension or rank of the tensor train. (The terms bond dimension and rank will be used interchangeably.) If the original dataset can be represented as a QTT of small bond dimension (ideally $D \sim \log (N)$
largest singular values at each decomposition step. This parameter is referred to as the bond dimension or rank of the tensor train. (The terms bond dimension and rank will be used interchangeably.) If the original dataset can be represented as a QTT of small bond dimension (ideally $D \sim \log (N)$![]() ) with only some small tolerable amount of error, the dataset is described as compressible and can be efficiently represented as a QTT. For concrete examples of common functions that can be efficiently represented in the QTT format, we refer the reader to the paper of Dolgov (Reference Dolgov2014, p. 56).
) with only some small tolerable amount of error, the dataset is described as compressible and can be efficiently represented as a QTT. For concrete examples of common functions that can be efficiently represented in the QTT format, we refer the reader to the paper of Dolgov (Reference Dolgov2014, p. 56).
Linear operators acting on $\textsf{h}(x)$![]() can also be expressed in the QTT format, resulting in the QTT-operator
can also be expressed in the QTT format, resulting in the QTT-operator

where each tensor $\textsf{M}^{(p)}$![]() now has two physical bonds ($o_p, i_p$
now has two physical bonds ($o_p, i_p$![]() ) that are used to access the output $x'$
) that are used to access the output $x'$![]() and input $x$
and input $x$![]() of the discretized operator $\textsf{O}$
of the discretized operator $\textsf{O}$![]() .
.
The QTT representation can be considered ‘quantum-inspired’ since mapping classical data onto a quantum computer could be done in a similar fashion (Lubasch, Moinier & Jaksch Reference Lubasch, Moinier and Jaksch2018; Lubasch et al. Reference Lubasch, Joo, Moinier, Kiffner and Jaksch2020; Garcia-Ripoll Reference Garcia-Ripoll2021; Jaksch et al. Reference Jaksch, Givi, Daley and Rung2023). In this case, each tensor would correspond to one qubit. The physical bond in the tensor represents the state of the qubit, while the virtual bonds capture the entanglement between the qubits. The QTT-operators are analogues to quantum gates or quantum circuits applied to the quantum computer.
More generally, for $K$![]() -dimensional functions, each of the $K$
-dimensional functions, each of the $K$![]() original dimensions is quantized. If the function is discretized using $d^L$
original dimensions is quantized. If the function is discretized using $d^L$![]() grid points along each of the original $K$
grid points along each of the original $K$![]() dimensions, then the quantization yields a $KL$
dimensions, then the quantization yields a $KL$![]() -dimensional tensor of size $d$
-dimensional tensor of size $d$![]() along each new dimension. When decomposing this tensor into a QTN, several different ansätze can be considered. Even if one continues to use the tensor train geometry, as is done in most works, one can opt to append tensors corresponding to different problem dimensions sequentially (figure 1a) (Ye & Loureiro Reference Ye and Loureiro2022; Kiffner & Jaksch Reference Kiffner and Jaksch2023; Kornev et al. Reference Kornev, Dolgov, Pinto, Pflitsch, Perelshtein and Melnikov2023; Peddinti et al. Reference Peddinti, Pisoni, Marini, Lott, Argentieri, Tiunov and Aolita2023) or in an interleaved fashion (figure 1b) (Gourianov et al. Reference Gourianov, Lubasch, Dolgov, van den Berg, Babaee, Givi, Kiffner and Jaksch2022). The caveat of sequential ordering is that interactions between different dimensions can be long-range. For example, any correlation between $x$
along each new dimension. When decomposing this tensor into a QTN, several different ansätze can be considered. Even if one continues to use the tensor train geometry, as is done in most works, one can opt to append tensors corresponding to different problem dimensions sequentially (figure 1a) (Ye & Loureiro Reference Ye and Loureiro2022; Kiffner & Jaksch Reference Kiffner and Jaksch2023; Kornev et al. Reference Kornev, Dolgov, Pinto, Pflitsch, Perelshtein and Melnikov2023; Peddinti et al. Reference Peddinti, Pisoni, Marini, Lott, Argentieri, Tiunov and Aolita2023) or in an interleaved fashion (figure 1b) (Gourianov et al. Reference Gourianov, Lubasch, Dolgov, van den Berg, Babaee, Givi, Kiffner and Jaksch2022). The caveat of sequential ordering is that interactions between different dimensions can be long-range. For example, any correlation between $x$![]() and $z$
and $z$![]() are long-range, and must be transmitted through all tensors corresponding to the $y$
are long-range, and must be transmitted through all tensors corresponding to the $y$![]() grid points. With the interleaved geometry, in which tensors are ordered by grid scale, interactions between different dimensions are typically not as long-range. However, this ordering is less efficient for separable functions and operators.
grid points. With the interleaved geometry, in which tensors are ordered by grid scale, interactions between different dimensions are typically not as long-range. However, this ordering is less efficient for separable functions and operators.

Figure 1. Tensor network diagrams for three-dimensional data. (a) Tensor train with tensors for different dimensions appended sequentially. (b) Tensor train with tensors for different dimensions combined in an interleaved fashion. (c) Comb-like tree tensor network with tensors for different dimensions on separate branches.
This work uses a comb-like tree tensor network (QTC) ansatz (also referred to as the QTT-Tucker format by Dolgov & Khoromskij Reference Dolgov and Khoromskij2013). In this ansatz, the original $K$![]() -dimensional function is first decomposed into a tensor train of $K$
-dimensional function is first decomposed into a tensor train of $K$![]() tensors without quantization, so the physical bonds of each tensor correspond to the original problem dimensions, and their sizes are the number of grid points used along the corresponding dimensions. Then, the physical bond of each tensor is quantized, and each tensor is decomposed into a QTT. The resulting QTN is depicted in figure 1(c); the grid points for each dimension are represented by separate 1-D tensor trains (the branches) and each TT is connected to each other via another tensor train (the spine; darker green). Mathematically, this can be written as
tensors without quantization, so the physical bonds of each tensor correspond to the original problem dimensions, and their sizes are the number of grid points used along the corresponding dimensions. Then, the physical bond of each tensor is quantized, and each tensor is decomposed into a QTT. The resulting QTN is depicted in figure 1(c); the grid points for each dimension are represented by separate 1-D tensor trains (the branches) and each TT is connected to each other via another tensor train (the spine; darker green). Mathematically, this can be written as

where $B^{(k)}$![]() is a tensor train for the $k$
is a tensor train for the $k$![]() th problem dimension
th problem dimension

To simplify notation, we assumed that all problem dimensions have the same number of grid points. However, this is not a necessary requirement. In (2.4), tensor $\tilde {\textsf{M}}^{(k)}$![]() is the $k$
is the $k$![]() th tensor in the spine of the comb. Note that it does not have a physical index. In the low-rank approximation, the size of each dimension is capped at $S$
th tensor in the spine of the comb. Note that it does not have a physical index. In the low-rank approximation, the size of each dimension is capped at $S$![]() . For simplicity, this work uses the same maximum bond dimension for all virtual bonds (i.e. $S=D$
. For simplicity, this work uses the same maximum bond dimension for all virtual bonds (i.e. $S=D$![]() ), though it may be advantageous to use different bond dimensions for the bonds in the branches ($\alpha _{(k,i)}$
), though it may be advantageous to use different bond dimensions for the bonds in the branches ($\alpha _{(k,i)}$![]() ), along the spine ($\gamma _k$
), along the spine ($\gamma _k$![]() ) and between the spine to the branches ($\beta _k$
) and between the spine to the branches ($\beta _k$![]() ).
).
The motivation for this ansatz is to reduce the distance along the tensor network between different dimensions, while maintaining an efficient representation for product states. Additionally, all algorithms for QTTs can be extended to the QTC geometry in a straightforward fashion, since the QTC geometry contains no loops and one can still define a centre of orthogonality. The computational costs of relevant algorithms are summarized in table 1 and described more in depth in the supplementary material available at https://doi.org/10.1017/S0022377824000503. The scaling of most algorithms is more expensive for the comb geometry because of the spine tensors, though this increased cost may be offset by increased representability, allowing one to use smaller bond dimension.
Table 1. Theoretical costs of the primary steps in the Vlasov–Maxwell solver for the tensor train (QTT) geometry and the spine in the comb geometry (QTC-Spine). In the QTT geometry, all vectors have bond dimension $D$![]() , while operators have bond dimension $D_W$
, while operators have bond dimension $D_W$![]() . In the spine of the comb tensor network, all bonds are of size $S$
. In the spine of the comb tensor network, all bonds are of size $S$![]() and $S_W$
and $S_W$![]() for the vectors and operators, respectively. Note that in practice, not all virtual bonds are necessarily of the same size, and the specified bond dimensions and the listed costs serve as upper bounds.
for the vectors and operators, respectively. Note that in practice, not all virtual bonds are necessarily of the same size, and the specified bond dimensions and the listed costs serve as upper bounds.

3. Problem overview
The collisionless Vlasov equation is given by
where $f_s$![]() is the time-dependent distribution function for particle species $s$
is the time-dependent distribution function for particle species $s$![]() with coordinates in real space ($\boldsymbol {x}$
with coordinates in real space ($\boldsymbol {x}$![]() ) and velocity space ($\boldsymbol {v}$
) and velocity space ($\boldsymbol {v}$![]() ), and $m_s$
), and $m_s$![]() is the particle mass. Here, $\boldsymbol {F}$
is the particle mass. Here, $\boldsymbol {F}$![]() denotes the force that the particles are subject to. In the case of plasma dynamics, the force of interest is the Lorentz force,
denotes the force that the particles are subject to. In the case of plasma dynamics, the force of interest is the Lorentz force,
where $q_s$![]() is the charge of particle species $s$
is the charge of particle species $s$![]() , $\boldsymbol {B}$
, $\boldsymbol {B}$![]() is the magnetic field and $\boldsymbol {E}$
is the magnetic field and $\boldsymbol {E}$![]() is the electric field. Both fields have coordinates in real space ($\boldsymbol {x}$
is the electric field. Both fields have coordinates in real space ($\boldsymbol {x}$![]() ) and vary over time.
) and vary over time.
For an electromagnetic system, one propagates the electric and magnetic fields forwards in time via Maxwell's equations,
where $c$![]() is the speed of light, $\varepsilon _0$
is the speed of light, $\varepsilon _0$![]() is the vacuum permittivity and $\boldsymbol {J} = \sum _s q_s \int {\rm d} \boldsymbol {v} \boldsymbol {v} f_s(\boldsymbol {x},\boldsymbol {v}{,t})$
is the vacuum permittivity and $\boldsymbol {J} = \sum _s q_s \int {\rm d} \boldsymbol {v} \boldsymbol {v} f_s(\boldsymbol {x},\boldsymbol {v}{,t})$![]() is the current density. The current density is the source of the nonlinearity, since the state of the plasma affects the electromagnetic force that is exerted on itself.
is the current density. The current density is the source of the nonlinearity, since the state of the plasma affects the electromagnetic force that is exerted on itself.
Equations (3.1)–(3.4) are the equations we wish to solve in our Vlasov–Maxwell solver.
4. Vlasov–Maxwell solver
We implement a semi-implicit finite-difference solver of the Vlasov–Maxwell equations using the QTN format. The distribution functions for each species and each component of the electromagnetic fields are represented as QTNs with bond sizes of at most $D$![]() . Likewise, the operators acting on these fields (e.g. the derivatives) are also represented in the QTN format (see § I of the supplementary material and Ye & Loureiro (Reference Ye and Loureiro2022) for details).
. Likewise, the operators acting on these fields (e.g. the derivatives) are also represented in the QTN format (see § I of the supplementary material and Ye & Loureiro (Reference Ye and Loureiro2022) for details).
The distribution functions are updated via explicit time integration of the Boltzmann equation, with second-order operating splitting between the $\boldsymbol {x}$![]() and $\boldsymbol {v}$
and $\boldsymbol {v}$![]() advection steps. For advection in $\boldsymbol {x}$
advection steps. For advection in $\boldsymbol {x}$![]() , a split-step semi-Lagrangian (SL) scheme is used; the operator is split further into 1-D advection steps using a second-order scheme (Durran Reference Durran2010). For advection in $\boldsymbol {v}$
, a split-step semi-Lagrangian (SL) scheme is used; the operator is split further into 1-D advection steps using a second-order scheme (Durran Reference Durran2010). For advection in $\boldsymbol {v}$![]() , a new time evolution scheme specific to QTNs and based on the time-dependent variational principle (TDVP) (Lasser & Su Reference Lasser and Su2022) is used. The electromagnetic fields are updated using a Crank–Nicolson time integration scheme, which is solved using an iterative scheme called the density matrix renormalization group (DMRG) (Dolgov & Savostyanov Reference Dolgov and Savostyanov2014).
, a new time evolution scheme specific to QTNs and based on the time-dependent variational principle (TDVP) (Lasser & Su Reference Lasser and Su2022) is used. The electromagnetic fields are updated using a Crank–Nicolson time integration scheme, which is solved using an iterative scheme called the density matrix renormalization group (DMRG) (Dolgov & Savostyanov Reference Dolgov and Savostyanov2014).
4.1. Ensuring positivity
One problem with solving the Vlasov equation in the QTN format is that taking the low-rank approximation of $f$![]() generally does not preserve important properties, such as its norm and positivity. The norm can be corrected by rescaling the distribution function. It should be possible to develop methods that conserve momentum and energy (as is done in the non-quantized low-rank community Einkemmer & Jospeh Reference Einkemmer and Jospeh2021; Coughlin, Hu & Shumlak Reference Coughlin, Hu and Shumlak2023) though these techniques are not implemented in this work. However, it is difficult to ensure positivity once in the QTN format.
generally does not preserve important properties, such as its norm and positivity. The norm can be corrected by rescaling the distribution function. It should be possible to develop methods that conserve momentum and energy (as is done in the non-quantized low-rank community Einkemmer & Jospeh Reference Einkemmer and Jospeh2021; Coughlin, Hu & Shumlak Reference Coughlin, Hu and Shumlak2023) though these techniques are not implemented in this work. However, it is difficult to ensure positivity once in the QTN format.
A simple fix is to define $g$![]() , such that $f=g^* g$
, such that $f=g^* g$![]() , and instead evolve $g$
, and instead evolve $g$![]() forwards in time. Plugging this into (3.1), we obtain
forwards in time. Plugging this into (3.1), we obtain
and an equivalent equation for $g^*$![]() . In the following calculations, we are actually solving (4.1) to ensure positivity in our calculations.
. In the following calculations, we are actually solving (4.1) to ensure positivity in our calculations.
4.2. Semi-Lagrangian time evolution
With operator splitting, higher-dimensional advection problems are simplified to a series of 1-D advection problems of the form
where $\psi$![]() is the field of interest and $u$
is the field of interest and $u$![]() is the advection coefficient that is constant along the $x$
is the advection coefficient that is constant along the $x$![]() -axis. However, $u$
-axis. However, $u$![]() will in general be variable in all other dimensions of the problem. In the SL time evolution scheme, one approximates the field as a set of parcels, computes their exact trajectories and then uses the updated parcels to estimate $\psi$
will in general be variable in all other dimensions of the problem. In the SL time evolution scheme, one approximates the field as a set of parcels, computes their exact trajectories and then uses the updated parcels to estimate $\psi$![]() at the next time step.
at the next time step.
Consider a uniform grid, with $x_j = j\Delta x$![]() , and let $\phi$
, and let $\phi$![]() denote a numerical approximation to field $\psi$
denote a numerical approximation to field $\psi$![]() ; here, $\phi _j=\psi (x_j)$
; here, $\phi _j=\psi (x_j)$![]() . Since there are no sources, $\phi$
. Since there are no sources, $\phi$![]() at the next time step is given by
at the next time step is given by
where $\tilde {x}_j^n = x_j - u\Delta t$![]() is the departure point of the trajectory starting at time $t^n$
is the departure point of the trajectory starting at time $t^n$![]() and arriving at $x_j$
and arriving at $x_j$![]() at the next time step $t^{n+1}$
at the next time step $t^{n+1}$![]() . In this work, the value of $\phi (\tilde {x}^n_j)$
. In this work, the value of $\phi (\tilde {x}^n_j)$![]() is obtained using a cubic interpolation. For $u > 0$
is obtained using a cubic interpolation. For $u > 0$![]() , this is given by (Durran Reference Durran2010)
, this is given by (Durran Reference Durran2010)

where $p$![]() is the integer part of $u \Delta t / \Delta x$
is the integer part of $u \Delta t / \Delta x$![]() , $\alpha =({x_{j-p} - \tilde {x}_j^n})/{\Delta x}$
, $\alpha =({x_{j-p} - \tilde {x}_j^n})/{\Delta x}$![]() and superscript $n$
and superscript $n$![]() denotes the time step. Thus, the next time step is obtained from $\phi ^{n+1} = \textsf{A}_{SL} \phi ^n$
denotes the time step. Thus, the next time step is obtained from $\phi ^{n+1} = \textsf{A}_{SL} \phi ^n$![]() , where the matrix $\textsf{A}_{SL}$
, where the matrix $\textsf{A}_{SL}$![]() encodes the above equation.
encodes the above equation.
Obtaining the QTN-Operator decomposition of $\textsf{A}_{SL}$![]() can be computationally expensive. At the moment, we do not have an analytical form for the QTN-Operator, even for constant $u$
can be computationally expensive. At the moment, we do not have an analytical form for the QTN-Operator, even for constant $u$![]() , and any expression one does obtain would be difficult to generalize to higher-dimensional problems with variable $u$
, and any expression one does obtain would be difficult to generalize to higher-dimensional problems with variable $u$![]() . One can compute the QTN-Operator numerically by performing a series of SVD operations in an iterative fashion (Oseledets & Tyrtyshnikov Reference Oseledets and Tyrtyshnikov2010). However, the cost of this naive but reliable procedure scales like $O(N^2)$
. One can compute the QTN-Operator numerically by performing a series of SVD operations in an iterative fashion (Oseledets & Tyrtyshnikov Reference Oseledets and Tyrtyshnikov2010). However, the cost of this naive but reliable procedure scales like $O(N^2)$![]() , where $N$
, where $N$![]() is the total number of grid points for the dimensions in which $u$
is the total number of grid points for the dimensions in which $u$![]() is not constant and the dimension along which the derivative is taken. Interpolation algorithms such as TT-Cross (Oseledets & Tyrtyshnikov Reference Oseledets and Tyrtyshnikov2010) often perform well for low-rank tensors, with computational costs that scale polynomially with rank. However, the resulting QTN is expected to require moderately large ranks, especially for larger time steps (Kormann Reference Kormann2015).
is not constant and the dimension along which the derivative is taken. Interpolation algorithms such as TT-Cross (Oseledets & Tyrtyshnikov Reference Oseledets and Tyrtyshnikov2010) often perform well for low-rank tensors, with computational costs that scale polynomially with rank. However, the resulting QTN is expected to require moderately large ranks, especially for larger time steps (Kormann Reference Kormann2015).
Fortunately, while SL time evolution in the QTN format does not appear to be advantageous for arbitrary problems, it can be relatively efficient for performing advection of the Vlasov equation along the spatial dimensions. For example, in the case of advection along the $x$![]() -axis,
-axis,
the operator $\textsf{A}_{SL}$![]() is effectively two-dimensional, as it can be written in the form $\textsf{A}_{SL} = \tilde {\textsf{A}}_{x,v_x} \otimes \mathbb {I}_{y,z,v_y,v_z}$
is effectively two-dimensional, as it can be written in the form $\textsf{A}_{SL} = \tilde {\textsf{A}}_{x,v_x} \otimes \mathbb {I}_{y,z,v_y,v_z}$![]() (the subscripts denote the problem dimensions on which the operator acts). It is observed that the rank of the QTN representation of $\tilde {\textsf{A}}_{x,v_x}$
(the subscripts denote the problem dimensions on which the operator acts). It is observed that the rank of the QTN representation of $\tilde {\textsf{A}}_{x,v_x}$![]() depends on the largest magnitude of integer $p$
depends on the largest magnitude of integer $p$![]() ; so long as moderate time step and grid resolution are used, the bond dimension remains manageable. Furthermore, if the time step is held constant, the QTN decomposition only needs to be performed once.
; so long as moderate time step and grid resolution are used, the bond dimension remains manageable. Furthermore, if the time step is held constant, the QTN decomposition only needs to be performed once.
Once in the QTT format, the matrix-vector multiplication is performed using the density-matrix method (McCulloch Reference McCulloch2007). Details of this algorithm for the comb geometry are given in § III of the supplementary material and the computational costs are listed in table 1. Since the bond dimension of the operator $\textsf{A}_{SL}$![]() is expected to be modest for all time, its contribution to the scaling can be neglected, yielding costs that are like $O(D^3)$
is expected to be modest for all time, its contribution to the scaling can be neglected, yielding costs that are like $O(D^3)$![]() for the QTT geometry and $O(D^4)$
for the QTT geometry and $O(D^4)$![]() for the QTC geometry. For the Orszag–Tang vortex calculation, the observed scaling is closer to $O(D^{2.5})$
for the QTC geometry. For the Orszag–Tang vortex calculation, the observed scaling is closer to $O(D^{2.5})$![]() (see § VI.A.4 of the supplementary material).
(see § VI.A.4 of the supplementary material).
4.3. Time-dependent variational principle
Thus far, prior works with QTNs use classical explicit time integrators (such as fourth-order Runge–Kutta (RK4) and MacCormack). Similar to the SL scheme discussed above, most explicit schemes only require matrix-vector multiplications and additions, and thus can easily be translated into the QTN format. These time integration schemes are also global schemes, since they involve manipulating the entire QTN state at once.
We can instead consider a local time evolution scheme, in which individual tensors in the QTN are propagated forwards in time in a sequential fashion. In quantum simulation, one such algorithm is the time-dependent variational principle (TDVP) scheme (Haegeman et al. Reference Haegeman, Lubich, Oseledets, Vandereycken and Verstraete2016). This scheme is also closely related to the dynamical low-rank algorithm (Khoromskij, Oseledets & Schneider Reference Khoromskij, Oseledets and Schneider2012; Einkemmer & Lubich Reference Einkemmer and Lubich2018), which has been used for solving PDEs in the non-quantized tensor train community. More recently, the same underlying principle has been used in a quantum algorithm for solving the Schr’odinger–Poisson equation (Cappelli et al. Reference Cappelli, Tacchino, Murante, Borgani and Tavernelli2024).
There are very fundamental differences between global and local time evolution. In global time evolution, the state is first propagated in time and then projected onto the manifold for QTT of rank $D$![]() . In contrast, in local schemes, the dynamics is approximated by projection onto that manifold. Because the state remains in the low-rank manifold and does not require compression of a high-rank object, local methods are cheaper than global methods.
. In contrast, in local schemes, the dynamics is approximated by projection onto that manifold. Because the state remains in the low-rank manifold and does not require compression of a high-rank object, local methods are cheaper than global methods.
TDVP uses the Dirac–Frenkel variational principle, which states that the dynamics of a unitary system at any given point in time lies in the tangent space of the current state (Frenkel Reference Frenkel1934; Lasser & Su Reference Lasser and Su2022). By treating each tensor in the QTN as a variational parameter, one can obtain the effective dynamics for each tensor (given by anti-Hermitian operator $\textsf{A}_\text {eff}^{(i)}$![]() for the $i$
for the $i$![]() th tensor) and sequentially evolve them forwards in time. More specifically, if the unitary dynamics acting on state $\psi$
th tensor) and sequentially evolve them forwards in time. More specifically, if the unitary dynamics acting on state $\psi$![]() is described by anti-Hermitian operator $\textsf{A}$
is described by anti-Hermitian operator $\textsf{A}$![]() , the equation of motion for the $i$
, the equation of motion for the $i$![]() th tensor in the QTN $\textsf{M}^{(i)}$
th tensor in the QTN $\textsf{M}^{(i)}$![]() is
is
with
assuming that the QTN is canonicalized such that the orthogonality centre is located at the $i$![]() th tensor. As a result, the original dynamics is decomposed into roughly $2KL$
th tensor. As a result, the original dynamics is decomposed into roughly $2KL$![]() equations of motion of size $O(D^2)$
equations of motion of size $O(D^2)$![]() . (The factor of two arises from the algorithm when sweeping across all tensors.) For a second-order scheme, one updates all the tensors sequentially in a sweeping fashion with increasing i and then decreasing i, using half of the original time step at each update. We refer the reader to § IV of the supplementary material and the paper of Paeckel et al. (Reference Paeckel, Köhler, Swoboda, Manmana, Schöllwöck and Hubig2019) for a more in-depth explanation and the algorithmic details.
. (The factor of two arises from the algorithm when sweeping across all tensors.) For a second-order scheme, one updates all the tensors sequentially in a sweeping fashion with increasing i and then decreasing i, using half of the original time step at each update. We refer the reader to § IV of the supplementary material and the paper of Paeckel et al. (Reference Paeckel, Köhler, Swoboda, Manmana, Schöllwöck and Hubig2019) for a more in-depth explanation and the algorithmic details.
In this work, (4.6) is solved using RK4, so the computational cost scales like $O(D^3 D_W d + D^2 D_W^2 d^2)$![]() , where $D_W$
, where $D_W$![]() is the bond dimension of the QTT-O representation for time evolution operator $\textsf{A}$
is the bond dimension of the QTT-O representation for time evolution operator $\textsf{A}$![]() . For the QTC geometry, treatment of the tensors along the spine formally scales like $O(S^2 S_W^3 + S^4 S_W^2)$
. For the QTC geometry, treatment of the tensors along the spine formally scales like $O(S^2 S_W^3 + S^4 S_W^2)$![]() , where $S$
, where $S$![]() and $S_W$
and $S_W$![]() are the bond dimensions of the spine tensors in the QTC representations of state $\psi$
are the bond dimensions of the spine tensors in the QTC representations of state $\psi$![]() and operator $\textsf{A}$
and operator $\textsf{A}$![]() .
.
In the case of the Vlasov equation with two spatial dimensions, $S_W$![]() can be neglected, but $D_W \sim D$
can be neglected, but $D_W \sim D$![]() due to the nonlinear term. Setting $S=D$
due to the nonlinear term. Setting $S=D$![]() , the overall expected scaling is $O(D^4)$
, the overall expected scaling is $O(D^4)$![]() , which is what is observed for the Orszag–Tang vortex calculation (see § VI.A.4 of the supplementary material).
, which is what is observed for the Orszag–Tang vortex calculation (see § VI.A.4 of the supplementary material).
The time evolution scheme presented above is the single-site variant of TDVP. By construction, the time-evolved state will always have the same bond dimension as the initial state. As a result, the algorithm is cheaper than global methods since it avoids needing to compress the state from an enlarged bond dimension. However, this feature can be problematic when the time-evolved state requires larger bond dimension, particularly when the initial bond dimension is very small. To counter this, one would typically use the slightly more expensive two-site variant in which two neighbouring tensors are updated simultaneously so the QTN bond dimension can be adjusted as needed. However, in our solver, single-site TDVP appears to be sufficient because it is used in conjunction with global time evolution schemes that already increase the QTN rank. For both variants, we found it imperative to use a global time evolution scheme such as RK4 for the first time step.
Particularly interesting is that even when (4.6) is solved approximately using RK4, we observe that the local methods allow one to use larger time steps than what global methods are limited to (e.g. by the Courant–Friedrich–Levy (CFL) constraint Courant, Friedrichs & Lewy Reference Courant, Friedrichs and Lewy1967). In the following example, it appears that the time steps of the local algorithm can be larger by about a factor of two. This is perhaps possible because global information is incorporated into the effective operator for each individual tensor. The ability to bypass CFL is crucial for QTN finite-difference solvers, as it allows one to use higher spatial resolution (for improved accuracy) without requiring one to significantly increase temporal resolution.
4.3.1. Advection with time-varying electric field
We demonstrate TDVP time evolution with the advection of a 0D2V uniform electron Maxwellian distribution in the presence of constant background magnetic field $B_{0,z} \hat {z}$![]() , and uniform but time-varying electric field $E_x(t) = E_0 \cos (\omega t) \hat {x}$
, and uniform but time-varying electric field $E_x(t) = E_0 \cos (\omega t) \hat {x}$![]() . The resulting dynamics is the drifting of the Maxwellian with velocities
. The resulting dynamics is the drifting of the Maxwellian with velocities
where $\omega _c = q B_0 /m$![]() and $B_0>0$
and $B_0>0$![]() , and
, and
for $\omega \neq 1$![]() . The drift velocity in the $z$
. The drift velocity in the $z$![]() direction remains constant and therefore is not considered. In the following calculations, we use units such that $B_0=1$
direction remains constant and therefore is not considered. In the following calculations, we use units such that $B_0=1$![]() and $q/m=-1$
and $q/m=-1$![]() .
.
We perform time evolution using a second-order SL scheme, fourth-order Runge–Kutta (RK4), and TDVP. The calculations use $2^L$![]() grid points along the $v_x$
grid points along the $v_x$![]() - and $v_y$
- and $v_y$![]() -axes (with bounds $[-12 v_{{\rm th}}, 12 v_{{\rm th}})$
-axes (with bounds $[-12 v_{{\rm th}}, 12 v_{{\rm th}})$![]() ). The test electron distribution is initialized with drift velocities $v_{x,0}=v_{y,0}=0$
). The test electron distribution is initialized with drift velocities $v_{x,0}=v_{y,0}=0$![]() and thermal velocity of 1, and is evolved until a time of 100 using time step $\Delta t$
and thermal velocity of 1, and is evolved until a time of 100 using time step $\Delta t$![]() . Because split-step schemes are used, the results are shown with respect to the smallest time-step used in the time-evolution scheme ($\Delta t_{{\rm step}}$
. Because split-step schemes are used, the results are shown with respect to the smallest time-step used in the time-evolution scheme ($\Delta t_{{\rm step}}$![]() ) for a more fair comparison. The calculations were performed using a sequential layout with data along both axes encoded via a binary mapping. Both second-order and fourth-order centred finite-difference stencils are considered.
) for a more fair comparison. The calculations were performed using a sequential layout with data along both axes encoded via a binary mapping. Both second-order and fourth-order centred finite-difference stencils are considered.
At each time step, the distribution function $|g(v_x,v_y)|^2$![]() obtained after time evolution is fit to a Maxwellian $\mathcal {M}$
obtained after time evolution is fit to a Maxwellian $\mathcal {M}$![]() , and the errors in the variance ($\epsilon _{\sigma }$
, and the errors in the variance ($\epsilon _{\sigma }$![]() ) and drift velocity ($\epsilon _{v}$
) and drift velocity ($\epsilon _{v}$![]() ) are computed as the norm of the differences of the fit with respect to the theoretical values along the two dimensions. The ‘error in the smoothness’ is quantified as
) are computed as the norm of the differences of the fit with respect to the theoretical values along the two dimensions. The ‘error in the smoothness’ is quantified as
where the derivatives are computed with a first-order finite-difference stencil. The total error of the simulation is the root-mean-square error, $\lVert \epsilon (t) \rVert / \sqrt {N_t}$![]() , where $N_t$
, where $N_t$![]() is the total number of time steps.
is the total number of time steps.
The results are shown in figure 2. Plots in figure 2(a) show that a bond dimension of $D=16$![]() is sufficiently large for these calculations, since the error is not reduced with increased bond dimension. In the single-site TDVP calculations, the bond dimension throughout the simulation is fixed at the bond dimension of the initial state, which is about $D=10$
is sufficiently large for these calculations, since the error is not reduced with increased bond dimension. In the single-site TDVP calculations, the bond dimension throughout the simulation is fixed at the bond dimension of the initial state, which is about $D=10$![]() . Plots in figure 2(b) show how error scales with increasing grid resolution, for fixed bond dimension $D=16$
. Plots in figure 2(b) show how error scales with increasing grid resolution, for fixed bond dimension $D=16$![]() and time step $\Delta t=0.1$
and time step $\Delta t=0.1$![]() . This time step is too large for RK4 with resolutions greater than $L=7$
. This time step is too large for RK4 with resolutions greater than $L=7$![]() , leading to numerical instabilities. In the SL case, increasing resolution most notably improves the error in the variance (temperature) of the Maxwellian, as well of the smoothness of the resulting distribution function. For TDVP, increasing resolution also reduces errors of the drift velocity, but the distribution function exhibits more numerical noise (larger $\epsilon _\nabla$
, leading to numerical instabilities. In the SL case, increasing resolution most notably improves the error in the variance (temperature) of the Maxwellian, as well of the smoothness of the resulting distribution function. For TDVP, increasing resolution also reduces errors of the drift velocity, but the distribution function exhibits more numerical noise (larger $\epsilon _\nabla$![]() ) at higher grid resolutions. Figure 2(c) compares errors for calculations with $D=16$
) at higher grid resolutions. Figure 2(c) compares errors for calculations with $D=16$![]() , $L=8$
, $L=8$![]() for different time steps. With SL time evolution, error in the drift velocity decreases with reduced time step, but the error in variance and smoothness increases. This suggests that the error arises from the projection of the Lagrangian dynamics onto the grid at each time step. With TDVP, for the calculation with the fourth-order finite-difference stencil, performance improves with reduced time step, as is expected since the sequential iterative updates have an associated commutation error. However, with the second-order stencil, reducing the time step does not reduce the error.
for different time steps. With SL time evolution, error in the drift velocity decreases with reduced time step, but the error in variance and smoothness increases. This suggests that the error arises from the projection of the Lagrangian dynamics onto the grid at each time step. With TDVP, for the calculation with the fourth-order finite-difference stencil, performance improves with reduced time step, as is expected since the sequential iterative updates have an associated commutation error. However, with the second-order stencil, reducing the time step does not reduce the error.

Figure 2. Rms errors in the dynamics for advection with time-varying electric field. Test parameters are set to be $\omega =0.4567$![]() , $E_0=0.9$
, $E_0=0.9$![]() and $B_{0,z}=1$
and $B_{0,z}=1$![]() . Calculations are performed with bond dimension $D$
. Calculations are performed with bond dimension $D$![]() , grid resolution $2^L$
, grid resolution $2^L$![]() along each dimension and time step $\Delta t$
along each dimension and time step $\Delta t$![]() . The finest interval of each time step is $\Delta t_{{\rm step}}$
. The finest interval of each time step is $\Delta t_{{\rm step}}$![]() . (a) Results for varied $D$
. (a) Results for varied $D$![]() , and fixed $L=8$
, and fixed $L=8$![]() and $\Delta t_{{\rm step}} = 0.0125$
and $\Delta t_{{\rm step}} = 0.0125$![]() . (b) Results for varied $L$
. (b) Results for varied $L$![]() , and fixed $D=16$
, and fixed $D=16$![]() and $\Delta t_{{\rm step}}= 0.05$
and $\Delta t_{{\rm step}}= 0.05$![]() . (c) Results for varied $\Delta t_{{\rm step}}$
. (c) Results for varied $\Delta t_{{\rm step}}$![]() , and fixed $L=8$
, and fixed $L=8$![]() and $D=16$
and $D=16$![]() . The dashed black lines depict multiples of the CFL limit. The different plots along each row are labelled with the time evolution scheme used: semi-Lagrangian (SL), fourth-order Runge–Kutta (RK4) and single-site TDVP. Errors with respect to analytical results for the variance (i.e. thermal velocity squared, green), drift velocity (blue) and smoothness of the Maxwellian distribution ((4.12); red) are plotted in different colours. The two symbols denote calculations performed with a second-order or fourth-order centred finite-difference stencil. By construction, the stencil plays no role in SL time evolution. Missing data are a result of numerical instabilities.
. The dashed black lines depict multiples of the CFL limit. The different plots along each row are labelled with the time evolution scheme used: semi-Lagrangian (SL), fourth-order Runge–Kutta (RK4) and single-site TDVP. Errors with respect to analytical results for the variance (i.e. thermal velocity squared, green), drift velocity (blue) and smoothness of the Maxwellian distribution ((4.12); red) are plotted in different colours. The two symbols denote calculations performed with a second-order or fourth-order centred finite-difference stencil. By construction, the stencil plays no role in SL time evolution. Missing data are a result of numerical instabilities.
In summary, as a local time evolution scheme, in practice, TDVP is computationally cheaper than both SL and RK4 time evolution. The above results show that both SL time evolution and TDVP allow one to take larger time steps than with explicit grid-based methods like RK4. However, note that when TDVP is performed with RK4 as the local time integrator (as is done here), there still exists a maximum time step above which time evolution becomes unstable. In general, the error in the thermal velocity is smaller with TDVP than SL time evolution (with which the Maxwellian tends to broaden). However, the distribution function from SL tends to be smoother than the results from TDVP. This may become problematic for long-time time integration using TDVP.
4.4. Implicit solver for Maxwell's equations
The electric and magnetic fields are propagated forwards in time implicitly using Crank–Nicolson. Given the fields at time step $n$![]() , the updated fields at the next time step are obtained by solving
, the updated fields at the next time step are obtained by solving

where $\boldsymbol {E}_0$![]() and $\boldsymbol {B}_0$
and $\boldsymbol {B}_0$![]() are time-invariant background contributions to the electric and magnetic fields, and $\boldsymbol {J}^n$
are time-invariant background contributions to the electric and magnetic fields, and $\boldsymbol {J}^n$![]() is the current density measured from the distribution functions at the $n$
is the current density measured from the distribution functions at the $n$![]() th time step.
th time step.
Linear equations of the form $\textsf{A}x=b$![]() can be solved approximately in the QTT format using the DMRG algorithm (Schollwöck Reference Schollwöck2011; Oseledets & Dolgov Reference Oseledets and Dolgov2012; Dolgov & Savostyanov Reference Dolgov and Savostyanov2014; Gourianov et al. Reference Gourianov, Lubasch, Dolgov, van den Berg, Babaee, Givi, Kiffner and Jaksch2022), in which each tensor (or pairs of neighbouring tensors) are optimized sequentially to minimize the cost function $x^{{\dagger}} \textsf{A} x - 2 x^{{\dagger}} b$
can be solved approximately in the QTT format using the DMRG algorithm (Schollwöck Reference Schollwöck2011; Oseledets & Dolgov Reference Oseledets and Dolgov2012; Dolgov & Savostyanov Reference Dolgov and Savostyanov2014; Gourianov et al. Reference Gourianov, Lubasch, Dolgov, van den Berg, Babaee, Givi, Kiffner and Jaksch2022), in which each tensor (or pairs of neighbouring tensors) are optimized sequentially to minimize the cost function $x^{{\dagger}} \textsf{A} x - 2 x^{{\dagger}} b$![]() . (Details are provided in § V of the supplementary material.) If the local optimizations are performed using conjugate gradient descent (or conjugate gradients squared (Sonneveld Reference Sonneveld1989) for non-Hermitian $\textsf{A}$
. (Details are provided in § V of the supplementary material.) If the local optimizations are performed using conjugate gradient descent (or conjugate gradients squared (Sonneveld Reference Sonneveld1989) for non-Hermitian $\textsf{A}$![]() ), then the algorithm primarily consists of tensor contractions and the cost of the algorithm scales like $O((D_x^2 D_b + D_b D_x^2) D_A^2)$
), then the algorithm primarily consists of tensor contractions and the cost of the algorithm scales like $O((D_x^2 D_b + D_b D_x^2) D_A^2)$![]() , where $D_x$
, where $D_x$![]() and $D_b$
and $D_b$![]() are the bond dimensions of QTT-States $x$
are the bond dimensions of QTT-States $x$![]() and $b$
and $b$![]() , and $D_A$
, and $D_A$![]() is the bond dimension of QTT-Operator $\textsf{A}$
is the bond dimension of QTT-Operator $\textsf{A}$![]() . For the operator in (4.13), $D_\textsf{A}$
. For the operator in (4.13), $D_\textsf{A}$![]() is moderate and independent of system size, since $\textsf{A}$
is moderate and independent of system size, since $\textsf{A}$![]() can be built directly from differential operators and the calculations are performed on a uniform Cartesian grid.
can be built directly from differential operators and the calculations are performed on a uniform Cartesian grid.
If the QTT bond dimension is sufficiently large and the time step is small enough such that matrix $\textsf{A}$![]() is well conditioned, then DMRG converges quickly to the expected solution. In practice, DMRG often converges to some value larger than the tolerated error threshold (of $10^{-6}$
is well conditioned, then DMRG converges quickly to the expected solution. In practice, DMRG often converges to some value larger than the tolerated error threshold (of $10^{-6}$![]() ). In this case, we split a single time step into at most four smaller equally sized time steps; if DMRG shows better convergence at each step, then we continue to solve Maxwell's equations with these reduced time steps. Otherwise, we simply accept that the QTT bond dimension is likely not large enough and continue with the simulation as is. Certainly, a more advanced implicit time evolution scheme should be considered in the future.
). In this case, we split a single time step into at most four smaller equally sized time steps; if DMRG shows better convergence at each step, then we continue to solve Maxwell's equations with these reduced time steps. Otherwise, we simply accept that the QTT bond dimension is likely not large enough and continue with the simulation as is. Certainly, a more advanced implicit time evolution scheme should be considered in the future.
Note that the DMRG algorithm can be extended to more general QTN geometries. However, in this work, we are only solving Maxwell's equation in two dimensions, and the QTC with two branches is equivalent to a QTT. As such, we do not need to modify the original algorithm.
5. Results
In the following section, we evaluate the performance of the proposed QTN methods on two common test problems. Our code is built off the Python tensor network software package quimb (Gray Reference Gray2018), though one could use any of the many other tensor network software packages available.
5.1. Orszag–Tang vortex
The Orszag–Tang vortex (Orszag & Tang Reference Orszag and Tang1979) is a well-documented nonlinear test problem that captures the onset and development of turbulence. We consider a (fully nonlinear and kinetic) 2D3V calculation with protons and electrons. The initial conditions are (Juno et al. Reference Juno, Hakim, TenBarge, Shi and Dorland2018)
where $k_x=k_y=2{\rm \pi} /L_\text {box}$![]() , with $L_\text {box}$
, with $L_\text {box}$![]() being the simulation domain size in real space. Here, $B_g$
being the simulation domain size in real space. Here, $B_g$![]() is the out-of-plane guide field. The amplitudes of the perturbations are set to $B_0 = 0.2B_g$
is the out-of-plane guide field. The amplitudes of the perturbations are set to $B_0 = 0.2B_g$![]() and $u_{0,p} = 0.2 v_{A,p}$
and $u_{0,p} = 0.2 v_{A,p}$![]() , where $v_{A,p} = B_g / \sqrt {\mu _0 n_0 m_p}$
, where $v_{A,p} = B_g / \sqrt {\mu _0 n_0 m_p}$![]() is the Alfvén velocity of the protons. The initial velocities ($\boldsymbol {u}_s$
is the Alfvén velocity of the protons. The initial velocities ($\boldsymbol {u}_s$![]() ) are included as initial drift velocities of the Maxwellian distribution,
) are included as initial drift velocities of the Maxwellian distribution,

where $v_{{\rm th},s}^2 = k_B T_s / m_s$![]() is the thermal velocity of species $s$
is the thermal velocity of species $s$![]() , with $k_B$
, with $k_B$![]() the Boltzmann constant, $m_s$
the Boltzmann constant, $m_s$![]() the mass and $T_s$
the mass and $T_s$![]() the temperature.
the temperature.
The plasma is initialized with density $n_0=1$![]() , mass ratio $m_p/m_e = 25$
, mass ratio $m_p/m_e = 25$![]() , temperature ratio of $T_p/T_e = 1$
, temperature ratio of $T_p/T_e = 1$![]() , proton plasma beta $\beta _p = 2 v^2_{{\rm th},p}/v^2_{A,p} = 0.08$
, proton plasma beta $\beta _p = 2 v^2_{{\rm th},p}/v^2_{A,p} = 0.08$![]() and speed of light $c = 50 v_{A,p}$
and speed of light $c = 50 v_{A,p}$![]() .
.
The simulation is performed with $L_\text {box}= 20.48 d_p$![]() , where $d_p = \sqrt { m_p / \mu _0 n_0 e^2}$
, where $d_p = \sqrt { m_p / \mu _0 n_0 e^2}$![]() is the proton skin depth, with $e$
is the proton skin depth, with $e$![]() being the elemental charge. The limits of the grid in velocity space for species $s$
being the elemental charge. The limits of the grid in velocity space for species $s$![]() are $\pm 7v_{{\rm th},s}$
are $\pm 7v_{{\rm th},s}$![]() . Periodic boundary conditions are used in all dimensions, including the velocity dimensions, so that the time evolution operator is unitary and TDVP can be used. The calculations are performed with $2^9$
. Periodic boundary conditions are used in all dimensions, including the velocity dimensions, so that the time evolution operator is unitary and TDVP can be used. The calculations are performed with $2^9$![]() grid points along each spatial axis and $2^6$
grid points along each spatial axis and $2^6$![]() grid points along each axis in velocity space. With this grid resolution, the grid spacing in real space is 0.04$d_p$
grid points along each axis in velocity space. With this grid resolution, the grid spacing in real space is 0.04$d_p$![]() , so the electron skin depth is well resolved. We use the QTC ansatz with tensors corresponding to each dimension on its own branch, ordered as $(x, y, v_x, v_y, v_z)$
, so the electron skin depth is well resolved. We use the QTC ansatz with tensors corresponding to each dimension on its own branch, ordered as $(x, y, v_x, v_y, v_z)$![]() , and the data are encoded with binary mapping such that fine grid tensors are attached to the spine for all dimensions. At each time step, the proton and electron distribution functions, as well as each component of the electric and magnetic fields, are compressed to bond dimension $D$
, and the data are encoded with binary mapping such that fine grid tensors are attached to the spine for all dimensions. At each time step, the proton and electron distribution functions, as well as each component of the electric and magnetic fields, are compressed to bond dimension $D$![]() .
.
Figure 3 shows the out-of-plane current density at time $21 \varOmega _{c,p}^{-1}$![]() obtained from simulations with bond dimension $D=32$
obtained from simulations with bond dimension $D=32$![]() in panel (a) and $D=64$
in panel (a) and $D=64$![]() in panel (b). Qualitatively, both calculations exhibit the expected dynamics. However, the features in the $D=32$
in panel (b). Qualitatively, both calculations exhibit the expected dynamics. However, the features in the $D=32$![]() calculation appear less sharp than in the $D=64$
calculation appear less sharp than in the $D=64$![]() case, and there is significantly more numerical noise. Unfortunately, the numerical noise will continue to grow for both calculations. Visual inspection suggests that the noise arises from the Maxwell equation solver in the electric field (see § VI.A.1 of the supplementary material for these plots). However, when increasing the bond dimension of the QTTs representing the electric and magnetic fields to $128$
case, and there is significantly more numerical noise. Unfortunately, the numerical noise will continue to grow for both calculations. Visual inspection suggests that the noise arises from the Maxwell equation solver in the electric field (see § VI.A.1 of the supplementary material for these plots). However, when increasing the bond dimension of the QTTs representing the electric and magnetic fields to $128$![]() , the noise actually worsens and one is limited to even shorter simulation times (figure 3c). It thus appears that the low-rank approximation provides some noise mitigation; with less compression, the noise grows unchecked.
, the noise actually worsens and one is limited to even shorter simulation times (figure 3c). It thus appears that the low-rank approximation provides some noise mitigation; with less compression, the noise grows unchecked.

Figure 3. Plots of the out-of-plane current for the Orszag–Tang vortex at the specified time for (a) $D=32$![]() , (b) $D=64$
, (b) $D=64$![]() , and (c) bond dimension $D_f=32$
, and (c) bond dimension $D_f=32$![]() for the distribution functions and bond dimension $D_{EM}=128$
for the distribution functions and bond dimension $D_{EM}=128$![]() for the electromagnetic fields. Calculations were performed with a time step of $0.001 \varOmega _{c,p}^{-1}$
for the electromagnetic fields. Calculations were performed with a time step of $0.001 \varOmega _{c,p}^{-1}$![]() .
.
Since the $D=32$![]() calculations yield broader features than the $D=64$
calculations yield broader features than the $D=64$![]() case, one might be tempted to say that the QTT is only able to capture features at an ‘effective grid resolution’ determined by $D$
case, one might be tempted to say that the QTT is only able to capture features at an ‘effective grid resolution’ determined by $D$![]() or the grid resolution for which the specified $D$
or the grid resolution for which the specified $D$![]() would yield no compression. (For the Orszag–Tang vortex calculation, since the EM fields are 2-D, $D=32$
would yield no compression. (For the Orszag–Tang vortex calculation, since the EM fields are 2-D, $D=32$![]() would yield no compression for a grid with 32 points along each dimension. This grid would have a grid-spacing of 0.64 $d_p$
would yield no compression for a grid with 32 points along each dimension. This grid would have a grid-spacing of 0.64 $d_p$![]() . For $D=64$
. For $D=64$![]() , the grid would have 64 points along each dimension and grid-spacing 0.32 $d_p$
, the grid would have 64 points along each dimension and grid-spacing 0.32 $d_p$![]() . These length scales also appear as special scales in the spectra; see § V1.A.1 of the supplementary material.) However, we stress that one should not interpret $D$
. These length scales also appear as special scales in the spectra; see § V1.A.1 of the supplementary material.) However, we stress that one should not interpret $D$![]() as an effective resolution. The observed correlation here is likely caused by numerical noise. Random and unstructured functions are not compressible in the QTT format. As such, numerical noise will likely reduce the compressibility of the original function. When compressing a noisy function, one typically will not obtain the original function. Instead, some noise will persist and continue to accumulate over time.
as an effective resolution. The observed correlation here is likely caused by numerical noise. Random and unstructured functions are not compressible in the QTT format. As such, numerical noise will likely reduce the compressibility of the original function. When compressing a noisy function, one typically will not obtain the original function. Instead, some noise will persist and continue to accumulate over time.
5.2. Reconnection problem
The next test we consider is the 2D3V GEM challenge (Birn & Hesse Reference Birn and Hesse2001): a magnetic reconnection set-up that has become a classical code-benchmark problem. As in the Orszag–Tang vortex test problem, we adapt the initial conditions to fully kinetic simulations (Schmitz & Grauer Reference Schmitz and Grauer2006; Allmann-Rahn et al. Reference Allmann-Rahn, Grauer and Kormann2022), with additional modifications so that periodic boundary conditions can be used.
In the traditional set-up, the initial configuration for each species $s$![]() is
is
where
is a uniform background distribution and $f_{0,s}$![]() is the Harris sheet equilibrium (Harris Reference Harris1962). Given the magnetic field
is the Harris sheet equilibrium (Harris Reference Harris1962). Given the magnetic field
where $\lambda$![]() is the thickness of the sheet, the proton/electron distribution is
is the thickness of the sheet, the proton/electron distribution is

where
The drift velocities are constrained by the equilibrium conditions,
The initial perturbation in the magnetic field is
To allow for periodic boundary conditions, the simulation domain (suppose previously $[-L_{\text {box},x}/2, L_{\text {box},x}/2 )$![]() and $[ -L_{\text {box},y}/2, L_{\text {box},y}/2 )$
and $[ -L_{\text {box},y}/2, L_{\text {box},y}/2 )$![]() ) is doubled in $y$
) is doubled in $y$![]() and an inverted Harris sheet placed at the simulation boundary:
and an inverted Harris sheet placed at the simulation boundary:
and
The perturbation in the magnetic field remains the same.
Simulations are performed with $L_{\text {box},x}=25.6 d_p$![]() , $L_{\text {box},y}=12.8 d_p$
, $L_{\text {box},y}=12.8 d_p$![]() and a Harris sheet thickness of $\lambda = 0.5 d_p$
and a Harris sheet thickness of $\lambda = 0.5 d_p$![]() . The plasma is defined to have a mass ratio of $m_p/m_e = 25$
. The plasma is defined to have a mass ratio of $m_p/m_e = 25$![]() , temperature ratio of $T_p/T_e = 5$
, temperature ratio of $T_p/T_e = 5$![]() , proton plasma beta $\beta _p = 5/6$
, proton plasma beta $\beta _p = 5/6$![]() and electron Alfvén velocity $v_{A,e}=0.25 c$
and electron Alfvén velocity $v_{A,e}=0.25 c$![]() . The strength of the perturbation is $A_0 = 0.1 B_0 d_p$
. The strength of the perturbation is $A_0 = 0.1 B_0 d_p$![]() . The background density is set to $n_b=0.2 n_0$
. The background density is set to $n_b=0.2 n_0$![]() . The limits of the grid in velocity space are $\pm 7.75 v_{{\rm th},p}$
. The limits of the grid in velocity space are $\pm 7.75 v_{{\rm th},p}$![]() for the protons. For the electrons, the limits are $\pm 7 v_{{\rm th},e}$
for the protons. For the electrons, the limits are $\pm 7 v_{{\rm th},e}$![]() in the $v_x$
in the $v_x$![]() and $v_y$
and $v_y$![]() directions, and $\pm 14 v_{{\rm th},e}$
directions, and $\pm 14 v_{{\rm th},e}$![]() in the $v_z$
in the $v_z$![]() direction. The resolution of the calculations are $2^8 \times 2^9 \times 2^7 \times 2^7 \times 2^8$
direction. The resolution of the calculations are $2^8 \times 2^9 \times 2^7 \times 2^7 \times 2^8$![]() along the $x\text -, y\text -, v_x\text -, v_y\text -$
along the $x\text -, y\text -, v_x\text -, v_y\text -$![]() and $v_z$
and $v_z$![]() -axes respectively. We again use the QTC ansatz with tensors corresponding to each dimension on its own branch. In contrast to above, the data are encoded with the mirror (two's complement) mapping for all dimensions because it showed marginally better results. Additionally, the bond dimension for the electric and magnetic fields are set to 128 so that the DMRG solver for Maxwell's equations might converge more quickly.
-axes respectively. We again use the QTC ansatz with tensors corresponding to each dimension on its own branch. In contrast to above, the data are encoded with the mirror (two's complement) mapping for all dimensions because it showed marginally better results. Additionally, the bond dimension for the electric and magnetic fields are set to 128 so that the DMRG solver for Maxwell's equations might converge more quickly.
Figure 4 shows the current density and figure 5 plots the reconnected magnetic flux $\varPsi = \int _0^{L_{\text {box},x}/2} B_y(x,y=0) \, {{\rm d} x}$![]() for calculations with bond dimensions $D=32$
for calculations with bond dimensions $D=32$![]() and $D=64$
and $D=64$![]() . Additional results are presented in § VI.B of the supplementary material. Again, for both bond dimensions considered here, we roughly obtain the expected reconnected flux over time (Schmitz & Grauer Reference Schmitz and Grauer2006). However, the dynamics appear sensitive to numerical noise, as evidenced by unexpected secondary island formation in the Harris sheet for the $D=32$
. Additional results are presented in § VI.B of the supplementary material. Again, for both bond dimensions considered here, we roughly obtain the expected reconnected flux over time (Schmitz & Grauer Reference Schmitz and Grauer2006). However, the dynamics appear sensitive to numerical noise, as evidenced by unexpected secondary island formation in the Harris sheet for the $D=32$![]() case.
case.

Figure 4. Out-of-plane current density for the GEM reconnection problem. Calculations were performed with with bond dimension (a) $D=32$![]() and (b) $D=64$
and (b) $D=64$![]() , and time step $\Delta t=0.005 \varOmega _{c,p}^{-1}$
, and time step $\Delta t=0.005 \varOmega _{c,p}^{-1}$![]() . Time is in units of $\varOmega _{c,p}^{-1}.$
. Time is in units of $\varOmega _{c,p}^{-1}.$![]()

Figure 5. Reconnected magnetic flux computed with time step $\Delta t=0.005 \varOmega _{c,p}^{-1}$![]() and bond dimension $D=32$
and bond dimension $D=32$![]() (blue) and $D=64$
(blue) and $D=64$![]() (orange). Time is in units of $\varOmega _{c,p}^{-1}$
(orange). Time is in units of $\varOmega _{c,p}^{-1}$![]() .
.
6. Discussion
The above results are a promising first demonstration that high-dimensional simulations of the Vlasov–Maxwell equations can be performed efficiently with the QTC ansatz. Our calculations use $N=2^{36}$![]() total grid points for the Orszag–Tang vortex and $N=2^{39}$
total grid points for the Orszag–Tang vortex and $N=2^{39}$![]() total grid points for the GEM reconnection problem. However, we are able to observe the expected phenomenological results satisfactorily with a maximum bond dimension of just $D=64$
total grid points for the GEM reconnection problem. However, we are able to observe the expected phenomenological results satisfactorily with a maximum bond dimension of just $D=64$![]() . Despite the computational overhead in the QTC algorithm, ignoring constant factors, the $O(D^4)$
. Despite the computational overhead in the QTC algorithm, ignoring constant factors, the $O(D^4)$![]() cost per time step is a fraction of the $O(N)$
cost per time step is a fraction of the $O(N)$![]() scaling for traditional methods and the simulations can be run on a single compute node. Furthermore, by using the local time evolution scheme TDVP, one can use a larger time step (observed to be larger by approximately a factor of 4) than allowed in global time evolution schemes. In addition to computational cost, memory storage costs are also reduced, from $O(N)$
scaling for traditional methods and the simulations can be run on a single compute node. Furthermore, by using the local time evolution scheme TDVP, one can use a larger time step (observed to be larger by approximately a factor of 4) than allowed in global time evolution schemes. In addition to computational cost, memory storage costs are also reduced, from $O(N)$![]() to $O(D^3)$
to $O(D^3)$![]() . Extension to full 3D3V calculations is straightforward, limited only by the current implementation of our code for the QTC geometry.
. Extension to full 3D3V calculations is straightforward, limited only by the current implementation of our code for the QTC geometry.
One can measure the efficiency of the QTN ansatz by measuring the von Neumann or bipartite entanglement entropy (EE) at each bond in the QTN. For simplicity, consider a QTT of length $L$![]() . The first $j$
. The first $j$![]() tensors form the left partition and the remaining tensors form the right partition. One can always partition the QTT via singular value decomposition, giving rise to
tensors form the left partition and the remaining tensors form the right partition. One can always partition the QTT via singular value decomposition, giving rise to
where $U$![]() and $V$
and $V$![]() are unitary matrices representing the left and right partitions, respectively, and $\varSigma$
are unitary matrices representing the left and right partitions, respectively, and $\varSigma$![]() is a diagonal matrix containing the singular values $\sigma$
is a diagonal matrix containing the singular values $\sigma$![]() . The EE is then given by
. The EE is then given by
where $\tilde {\sigma }$![]() are the singular values normalized by $\sum _i \sigma _i^2 = 1$
are the singular values normalized by $\sum _i \sigma _i^2 = 1$![]() . The minimum EE of zero occurs when there is only one non-zero singular value. Maximum entanglement occurs when all of the singular values are of equal weight, which would be $\log _2(D)$
. The minimum EE of zero occurs when there is only one non-zero singular value. Maximum entanglement occurs when all of the singular values are of equal weight, which would be $\log _2(D)$![]() for a bond of size $D$
for a bond of size $D$![]() . A smaller EE suggests that one can typically use a smaller bond dimension for the QTN. However, note that while the EE describes the amount of information transferred along the virtual bond, it does not provide information about the error that would arise from truncating the singular values.
. A smaller EE suggests that one can typically use a smaller bond dimension for the QTN. However, note that while the EE describes the amount of information transferred along the virtual bond, it does not provide information about the error that would arise from truncating the singular values.
We compute the EE at each bond in the QTC for the ion distribution, electron distribution, electric fields and magnetic fields. Results for the Orszag–Tang vortex are shown in figure 6 and results for the reconnection problem are shown in figure 7. Interestingly, in both cases, the EE of the ion and electron distributions remain relatively small, and the EE of the electric and magnetic fields tend to grow. Some of that is likely due to noise, as suggested by the sudden increase in EE and the visible increase of noise in the fields themselves (see §§ VI.A.2 and VI.B.2 supplementary material for these figures). Most of the noise appears to be injected through the electric field. This suggests that the issue is likely not due to insufficient bond dimension but rather numerical noise injected through various stages of the solver. This may be because our current QTT format solvers (i.e. TDVP and DMRG) are prone to introducing noise, but it also may be due to the simulation parameters used—the time step may have been too large for the Crank–Nicolson scheme and the grid resolution used still is not fine enough to resolve the electron Debye length. We intend to further investigate and characterize potential sources of numerical noise so that these issues can be remedied in the future.

Figure 6. Entanglement entropy at each bond for the Orszag–Tang problem. Bond number is ordered by bonds in the spine and then bonds in each branch.

Figure 7. Entanglement entropy at each bond for the reconnection problem. Bond number is ordered by bonds in the spine and then bonds in each branch.
Fortunately, it should be possible to improve upon our basic implementation to obtain better results. For example, as with most local optimization schemes, the DMRG solver used for the implicit time evolution of Maxwell's equations is prone to slow convergence and only finding local minima, particularly when the bond dimension is small. Our current implementation is very simple; using a preconditioner and a better initial guess will likely improve performance. One might also benefit from adding additional constraints, such as one to preferentially find smooth results, to help improve convergence. Whether or not these constraints can also be used to improve numerical stability of the implicit solver is also worth more in-depth investigation. Alternatively, one could include a filter or artificial dissipation that removes grid-scale noise. Preliminary results of the Orszag–Tang vortex calculation performed with an uncentred Crank–Nicolson scheme are shown in § VI.B.3 of the supplementary material.
In addition to improving our solver for Maxwell's equations, we also need to improve our understanding of the TDVP time evolution scheme. In particular, while single-site TDVP time evolution is used in this work with promising results, local tangent-space time evolution schemes need be examined further, since they have their limitations. Most notably, TDVP (both 1-site and 2-site) is known to sometimes yield incorrect dynamics (Yang & White Reference Yang and White2020), even as one reduces the time step. Understanding the lack of convergence with respect to time step and grid resolution must be addressed to trust results for problems to which we do not know the solution. Additionally, when using TDVP with RK4, there still is a time-step constraint, but we currently do not have an estimate for it. We also need to extend TDVP to non-Hermitian systems to account for non-periodic boundary conditions, so that a greater variety of problems can be considered. This should be straightforward, as any non-Hermitian system can be embedded in a Hermitian system that is twice the original system size. It may be possible to improve our basic implementation to better ensure conservation laws. For example, for simulation of closed quantum systems, the TDVP algorithm naturally conserves system energy and system norm, because the Hamiltonian describes both system energy and dynamics. Though this is not true in the case of the Vlasov equation, there may be an alternative formulation that allows one to take advantage of these conservation properties. There also may be ways to impose additional conservation properties, as is done in the dynamical low-rank literature (Einkemmer & Lubich Reference Einkemmer and Lubich2019; Einkemmer, Ostermann & Piazzola Reference Einkemmer, Ostermann and Piazzola2020; Einkemmer & Jospeh Reference Einkemmer and Jospeh2021).
As of now, our code runs serially on a single CPU node, with the exception of the internal threading performed by Python's numpy package. As such, while the amount of resources required to perform and store these calculations is much less than conventional methods, the overall run-time is likely longer than that of an optimized solver. The most expensive steps in the calculation are the advection in velocity space and the DMRG solver of the EM fields when many iterations are required. As mentioned earlier in this section, the DMRG solver can be improved by using a preconditioner to achieve faster convergence. For the advection step, since the bulk of the cost arises during tensor contraction, the runtime could be improved by distributing those calculations. However, a more fundamental problem is that the QTN algorithms discussed here are inherently serial, thus making parallel calculations unattractive. The QTC geometry may be more amenable for parallelization, with algorithms modified to allow one to work with each branch independently. However, computations on the spine generally have worse scaling than the branches and would face the same challenges for parallelization as QTTs. While parallelized algorithms for tensor trains do exist (Secular et al. Reference Secular, Gourianov, Lubasch, Dolgov, Clark and Jaksch2020), they must be carefully investigated and tested, as they may introduce additional errors and are prone to numerical instabilities. The parallelized algorithms will likely also be less efficient than serial algorithms, requiring repetitive calculations. For example, instead of computing the necessary information for just one branch and then building the information for the remaining branches as one proceeds through the algorithm, one may need to compute the required information for each branch all at once. However, given the low computational costs of the serial algorithm for modest bond dimension, increasing the cost linearly with problem dimension for parallelization is affordable.
One might argue that the observed efficiency and compressibility of the QTN representation is due to the inefficiency of the grid-based representation, and one could instead use a spectral or finite-element basis. Juno et al. (Reference Juno, Hakim, TenBarge, Shi and Dorland2018) reports a discontinuous Galerkin finite element calculation of the Orszag–Tang vortex with similar parameters. They use a $40^2\times 8^3$![]() grid in 2D3V and a second-order polynomial basis, resulting in $N_p = 112$
grid in 2D3V and a second-order polynomial basis, resulting in $N_p = 112$![]() degrees of freedom per grid cell. Thus, the distribution function is represented using $N N_p$
degrees of freedom per grid cell. Thus, the distribution function is represented using $N N_p$![]() ($9 \times 10^7$
($9 \times 10^7$![]() ) degrees of freedom (DOFs), which is greater than the approximate upper bound of $5D^3$
) degrees of freedom (DOFs), which is greater than the approximate upper bound of $5D^3$![]() for the QTC ansatz ($1.3 \times 10^6$
for the QTC ansatz ($1.3 \times 10^6$![]() DOFs for $D=64$
DOFs for $D=64$![]() ). By this rough comparison, the QTC ansatz indeed provides a smaller but approximate representation of the distribution function. For reference, newer finite-element simulations on a $112^2 \times 16^3$
). By this rough comparison, the QTC ansatz indeed provides a smaller but approximate representation of the distribution function. For reference, newer finite-element simulations on a $112^2 \times 16^3$![]() grid up to a time of $75\varOmega _{c,p}^{-1}$
grid up to a time of $75\varOmega _{c,p}^{-1}$![]() used 10k node-hours (Juno et al. Reference Juno, Hakim, TenBarge, Shi and Dorland2018; Hakim & Juno Reference Hakim and Juno2020; Hakim et al. Reference Hakim, Francisquez, Juno and Hammett2020).
used 10k node-hours (Juno et al. Reference Juno, Hakim, TenBarge, Shi and Dorland2018; Hakim & Juno Reference Hakim and Juno2020; Hakim et al. Reference Hakim, Francisquez, Juno and Hammett2020).
In comparison to non-quantized low-rank methods, the proposed QTN method exhibits a much more modest reduction in computational resources for the problems discussed above. One advantage of the QTN methods is the ability to use time steps somewhat larger than the CFL limit because of the local time evolution scheme, without having to perform semi-Lagrangian time evolution. Furthermore, QTNs are more likely to demonstrate a bigger advantage for problems requiring orders of magnitude more grid points along each dimension, as will be necessary for more realistic problems (e.g. with the proper mass ratio). A more thorough investigation on the efficiency of the QTN format for different simulation parameters needs to be performed. Additionally, testing the proposed algorithm for more complex problems, including those in different coordinate systems and especially those that are currently not tractable using conventional methods, is certainly worth pursuing. The QTN format is also not limited to a real-space, grid-based interpretation. Since the convolution operation can be performed efficiently within the QTN format (Kazeev, Khoromskij & Tyrtyshnikov Reference Kazeev, Khoromskij and Tyrtyshnikov2013a), one can also implement an efficient QTN solver with spectral bases. Spectral representations are often more compact than grid-based representations, so the degree to which QTNs can further compress these representations should be measured. Existing work also discusses finite-element solvers in the QTN format (Kazeev et al. Reference Kazeev, Oseledets, Rakhuba and Schwab2017; Kazeev & Schwab Reference Kazeev and Schwab2018; Kazeev et al. Reference Kazeev, Oseledets, Rakhuba and Schwab2022; Kornev et al. Reference Kornev, Dolgov, Pinto, Pflitsch, Perelshtein and Melnikov2023). Performing a careful comparison to understand the benefits and caveats of using different representations would be of practical interest and may improve our understanding of QTNs more generally.
There are many immediate and practical uses for QTN-based solvers. Because the low-rank approximations in the QTN format are solely numerical, one is able to solve the Vlasov equation at reduced cost without relying on assumptions that would limit the range of problems that can be studied. As such, one could perform a rough parameter sweep using the proposed solver before identifying a specific regime in which more accurate calculations are needed. The QTN solvers can also help with generating approximate but physically accurate training data for machine learning methods.
Lastly, we also hope that the QTN representation can act as another tool for understanding turbulence. Drawing from ideas in quantum information theory, one can better understand information flow between different length scales. Additionally, by connecting QTNs to other concepts like wavelets (Oseledets & Tyrtyshnikov Reference Oseledets and Tyrtyshnikov2011) and renormalization group, one may be able to build a consistent picture between different interpretations.
7. Conclusion
Understanding the nonlinear behaviour of collisionless plasmas requires first-principles descriptions such as provided by the coupled Vlasov–Maxwell system of equations. However, solving the Vlasov equation with traditional numerical algorithms is extremely resource-intensive, so an alternative approach that offers significantly reduced computational cost but nonetheless captures the important physical effects is very much needed. To address this problem, in this work we pioneer a grid-based Vlasov–Maxwell solver using a quantum-inspired approach: the quantized tensor network (QTN) format. Moreover, we use semi-Lagrangian time integration and a QTN time evolution scheme, both of which allow for time steps somewhat larger than the CFL limit. The cost of our algorithm at worst scales roughly like $O(D^4)$![]() , where $D$
, where $D$![]() is the rank or bond dimension of the QTN and determines the accuracy of the calculation. In the test cases considered, we find that QTNs of at most $D=64$
is the rank or bond dimension of the QTN and determines the accuracy of the calculation. In the test cases considered, we find that QTNs of at most $D=64$![]() are sufficient for capturing the expected dynamics with reasonable accuracy, even though the simulation is performed on grids of approximately $2^{36}$
are sufficient for capturing the expected dynamics with reasonable accuracy, even though the simulation is performed on grids of approximately $2^{36}$![]() grid points in total. This success suggests that the quantum-inspired representation can compress the Vlasov equation without significant loss of relevant physical effects, and thus may be a useful tool for interpreting and exploiting the multi-scale properties of plasma dynamics. More practically, the low-rank calculation offers an approximately $10^5$
grid points in total. This success suggests that the quantum-inspired representation can compress the Vlasov equation without significant loss of relevant physical effects, and thus may be a useful tool for interpreting and exploiting the multi-scale properties of plasma dynamics. More practically, the low-rank calculation offers an approximately $10^5$![]() reduction in the number of degrees of freedom compared with the corresponding traditional finite-difference representation and a $10^2$
reduction in the number of degrees of freedom compared with the corresponding traditional finite-difference representation and a $10^2$![]() reduction with respect to a comparable finite-element calculation. Due to the significant reduction in degrees of freedom and larger time steps, these simulations require significantly fewer resources than conventional numerical methods. Critically, despite achieving much greater efficiencies, the key physical processes of the test problems investigated are retained. Therefore, we expect that QTN-based algorithms will enable Vlasov simulations that would have remained out of reach with conventional numerical methods, and thus accelerate the pace of discovery in plasma physics and associated fields.
reduction with respect to a comparable finite-element calculation. Due to the significant reduction in degrees of freedom and larger time steps, these simulations require significantly fewer resources than conventional numerical methods. Critically, despite achieving much greater efficiencies, the key physical processes of the test problems investigated are retained. Therefore, we expect that QTN-based algorithms will enable Vlasov simulations that would have remained out of reach with conventional numerical methods, and thus accelerate the pace of discovery in plasma physics and associated fields.
Supplementary material
Supplementary material are available at https://doi.org/10.1017/S0022377824000503.
Acknowledgements
E.Y. thanks J. Juno for discussions regarding the cost of the discrete-Galerkin finite-element Vlasov solver in Gkeyll.
Editor Luís O. Silva thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
The authors were supported by awards DE-SC0020264 and DE-SC0022012 from the Department of Energy.
Code availability
Code can be made available upon request.