2 Assisted dynamical Schwinger process

In this section we consider pair production in the spirit of the Schwinger process, i.e. the creation of $e^{\pm }$ pairs by a purely electric background field which is assumed to be spatially homogeneous. In the following, we use the notation and formalism as introduced in Otto et al. (Reference Otto, Seipt, Blaschke, Kämpfer and Smolyansky2015a ). The quantum kinetic equation (Schmidt et al. Reference Schmidt, Blaschke, Röpke, Smolyansky, Prozorkevich and Toneev1998)

(2.1) $$\begin{eqnarray}{\dot{f}}(\boldsymbol{p},t)=\frac{{\it\lambda}(\boldsymbol{p},t)}{2}\int _{-\infty }^{t}\,\text{d}t^{\prime }{\it\lambda}(\boldsymbol{p},t^{\prime })(1-2f(\boldsymbol{p},t^{\prime }))\cos {\it\theta}(\boldsymbol{p},t,t^{\prime })\end{eqnarray}$$

determines the time $(t)$ evolution of the dimensionless phase space distribution function per spin projection degree of freedomFootnote ²   $f(\boldsymbol{p},t)=\text{d}N(\boldsymbol{p},t)/\text{d}^{3}p\,\text{d}^{3}x$ , where $N$ refers to the particle number and $\text{d}^{3}p$ and $\text{d}^{3}x$ are the three-dimensional volume elements in momentum ( $p$ ) and configuration ( $x$ ) spaces. We emphasize that only $f(\boldsymbol{p},t\rightarrow +\infty )$ can be considered as single particle distribution which may represent the source term of a subsequent time evolution of the emerging $e^{+}e^{-}$ plasma. The initial condition for solving (2.1) is $f(\boldsymbol{p},t\rightarrow -\infty )=0$ . Screening and back-reaction are not included by virtue of the small values of $f$ in subcritical fields (cf. Gelis & Tanji (Reference Gelis and Tanji2013) for recent work on that issue). The quantity ${\it\lambda}(\boldsymbol{p},t)=(eE(t)\,{\it\varepsilon}_{\bot }(p_{\bot }))/{\it\varepsilon}^{2}(\boldsymbol{p},t)$ stands for the amplitude of the vacuum transition, and ${\it\theta}(\boldsymbol{p},t,t^{\prime })=2\int _{t^{\prime }}^{t}\,\text{d}{\it\tau}\,{\it\varepsilon}(\boldsymbol{p},{\it\tau})$ stands for the dynamical phase, describing the vacuum oscillations modulated by the external field; the quasi-energy ${\it\varepsilon}$ , the transverse energy ${\it\varepsilon}_{\bot }$ and the longitudinal quasi-momentum $P$ are defined as ${\it\varepsilon}(\boldsymbol{p},t)=\sqrt{{\it\varepsilon}_{\bot }^{2}(p_{\bot })+P^{2}(p_{\Vert },t)}$ and ${\it\varepsilon}_{\bot }(p_{\bot })=\sqrt{m^{2}+p_{\bot }^{2}},$ $P(p_{\Vert },t)=p_{\Vert }-eA(t),$ where $p_{\bot }=|\boldsymbol{p}_{\bot }|$ is the modulus of the kinetic momentum ( $\boldsymbol{p}$ ) component of positrons (electrons) perpendicular to the electric field and $p_{\Vert }$ denotes the $E$ -parallel kinetic momentum component. The electric field follows from the potential

(2.2) $$\begin{eqnarray}A=K({\it\omega}t)\left(\frac{E_{1}}{{\it\omega}}\cos ({\it\omega}t)+\frac{E_{2}}{N{\it\omega}}\cos (N{\it\omega}t)\right)\end{eqnarray}$$

by $E=-{\dot{A}}$ in the Hamilton gauge. Equation (2.2) describes a bi-frequent field with frequency ratio $N$ (integer) and field strengths $E_{1}$ (the strong field ‘1’) and $E_{2}$ (the weak field ‘2’). The quantity $K$ is the common envelope function with the properties (i) absolutely flat in the flat-top time interval $-t_{\mathit{f.t.}}/2<t<+t_{\mathit{f.t.}}/2$ ; (ii) absolutely zero for $t<-t_{\mathit{f.t.}}/2-t_{\mathit{ramp}}$ and $t>t_{\mathit{f.t.}}/2+t_{\mathit{ramp}}$ ; and (iii) absolutely smooth everywhere, i.e. $K$ belongs to the $C^{\infty }$ class; $t_{\mathit{ramp}}$ is the ramping duration characterizing the switching on/off time intervals.

Figure 1. (a–c) Asymptotic transverse momentum ( $p_{\bot }$ ) spectrum at $p_{\Vert }=0$ for the bi-frequent field (2.2) (b) and the field components ‘1’ (a), ( $E_{1}=0.1E_{c}$ , ${\it\omega}=0.02m$ ) and ‘2’ (c), ( $E_{2}=0.05E_{c}$ , $N=25$ ) alone. (d–f): Fourier zero-modes $2{\it\Omega}(p_{\bot },p_{\Vert }=0)$ scaled by ${\it\omega}$ (d,e) and $N{\it\omega}$ (f) for the fields in (a–c) with resonance conditions (horizontal dashed lines for $\ell =341$ and $343$ (a,d; higher- $\ell$ resonances are not depicted since the peaks are underneath the scale displayed in (a)), $\ell =341,\ldots ,373$ (b,e) and $\ell =5$ (c,f); vertical dashed lines are for the resonance positions; peaks for even $\ell$ appear only for $p_{\Vert }\neq 0$ but get a zero amplitude at $p_{\Vert }=0$ , and thus their positions are not depicted).

Figure 1(a) exhibits three examples for the transverse phase space distribution $f(p_{\bot },p_{\Vert }=0,t\rightarrow \infty )$ for $E_{1}=0.1E_{c}$ , $E_{2}=0.05E_{c}$ , ${\it\omega}=0.02m$ , $N=25$ , $t_{\mathit{ramp}}=5{\it\omega}^{-1}$ and $t_{\mathit{f.t.}}=25{\it\omega}^{-1}$ obtained by numerically solving (2.1). The chosen parameters are still far from reach at present or near-future facilities. Due to the periodicity of the involved fields and their finite duration a pronounced peak structure emerges (the peaks become sharp, elliptically bent ridges with deep notches when continuing the spectrum to finite values of $p_{\Vert }$ ). The peak heights scale with $t_{\mathit{f.t.}}^{2}$ where the pulse duration is not too long. The peak positions are determined by the resonance condition (Otto et al. Reference Otto, Seipt, Blaschke, Kämpfer and Smolyansky2015a )

(2.3) $$\begin{eqnarray}2{\it\Omega}(p_{\bot },p_{\Vert })-\ell {\it\omega}=0,\end{eqnarray}$$

where

(2.4) $$\begin{eqnarray}{\it\Omega}=\frac{m}{2{\rm\pi}}\int _{0}^{2{\rm\pi}}\,\text{d}x\sqrt{1+(p_{\bot }/m)^{2}+[(p_{\Vert }/m)-{\it\gamma}_{1}^{-1}\cos x-{\it\gamma}_{2}^{-1}\cos Nx]^{2}}\end{eqnarray}$$

is the Fourier zero-mode of ${\it\varepsilon}$ . The values of $\ell$ (integer) where the resonance condition (2.3) is fulfilled can be used to label the peaks. The quantity ${\it\Omega}(p_{\bot }=p_{\Vert }=0)$ may be interpreted as effective mass $m^{\ast }$ (Kohlfürst, Gies & Alkofer Reference Kohlfürst, Gies and Alkofer2014) which determines $\ell _{\mathit{min}}=\text{int}(1+2m^{\ast }/{\it\omega})$ . The Fourier zero-modes as functions of $p_{\bot }$ at $p_{\Vert }=0$ are displayed in the bottom row in figure 1 together with the resonance positions. For the field ‘1’ alone (d) one has to take the limit ${\it\gamma}_{2}\rightarrow \infty$ in the Fourier zero-mode, while field ‘2’ alone (f) corresponds to ${\it\gamma}_{1}\rightarrow \infty$ and the replacement ${\it\omega}\rightarrow N{\it\omega}$ in (2.3).

Figure 2. Time evolution of $f(p_{\bot }=p_{\Vert }=0,t)$ in the adiabatic basis for the Sauter pulse (2.5) for ${\it\tau}=1~\text{m}^{-1}$ (blue), ${\it\tau}=2~\text{m}^{-1}$ (green), ${\it\tau}=5~\text{m}^{-1}$ (red), ${\it\tau}=10~\text{m}^{-1}$ (cyan), ${\it\tau}=20~\text{m}^{-1}$ (purple) and ${\it\tau}=50~\text{m}^{-1}$ (yellow), where $E_{0}=0.2E_{c}$ (a) and $E_{0}=0.15E_{c}$ (b). The dashed black curves depict the Schwinger case as the limit of large values of ${\it\tau}$ . Note the vast drop of the residual phase space occupancy for larger values of ${\it\tau}$ when changing $E_{0}$ from $0.2E_{c}$ to $0.15E_{c}$ .

The striking feature in figure 1 (cf. Otto et al. (Reference Otto, Seipt, Blaschke, Kämpfer and Smolyansky2015a ,Reference Otto, Seipt, Blaschke, Smolyansky and Kämpfer b ) for other examples with different parameters, in particular $t_{\mathit{f.t.}}$ , and Hähnel (Reference Hähnel2015) for a wider range of field strengths) is the lifting of the spectrum related to field ‘1’ by the assistance of field ‘2’. While the amplification of the created pair distribution by the assistance field can be huge, for sub-critical fields the frequency $N{\it\omega}$ must be $O(m)$ to overcome the exponential suppression. This implies that the intensities envisaged in ELI pillar IV (ELI 2015) must be at our disposal in conjunction with much higher frequencies to arrive at measurable pair numbers enhanced further by an assistant field (Otto et al. Reference Otto, Seipt, Blaschke, Smolyansky and Kämpfer2015b ).

Even with low pair creation probability, a once produced pair may seed a further avalanche evolution (Bell & Kirk Reference Bell and Kirk2008; Elkina et al. Reference Elkina, Fedotov, Kostyukov, Legkov, Narozhny, Nerush and Ruhl2011; King, Elkina & Ruhl Reference King, Elkina and Ruhl2013) toward an electron–positron plasma. In this respect one may ask for the time scales to approach the asymptotic out-state. A unique answer seems not to be achievable within the present framework due to the unavoidable ambiguity of the particle definition (see e.g. Dabrowski & Dunne (Reference Dabrowski and Dunne2014) for examples of changing the time evolution of $f$ at intermediate times when changing the basis). Having this disclaimer in mind one can nevertheless inspect graphs of $f(t)$ . Figure 2 exhibits the time evolution in the adiabatic basis for the Sauter pulse

(2.5) $$\begin{eqnarray}\displaystyle E(t)=\frac{E_{0}}{\cosh ^{2}(t/{\it\tau})} & & \displaystyle\end{eqnarray}$$

which is fairly different from (2.2). The analytical solution (Narozhny & Nikishov Reference Narozhny and Nikishov1970; Hebenstreit Reference Hebenstreit2011) of (2.1) is useful for checking numerical codes which are challenged by dealing with rapidly changing functions over many orders of magnitude. For large values of the pulse duration parameter ${\it\tau}$ the Schwinger case is recovered, see Hebenstreit (Reference Hebenstreit2011):

(2.6) $$\begin{eqnarray}f=\frac{1}{8}\left(1+\frac{u}{\sqrt{2\hat{{\it\eta}}+u^{2}}}\right)\text{e}^{-({\rm\pi}\hat{{\it\eta}})/4}|X+Y|^{2},\end{eqnarray}$$

with

(2.7a,b ) $$\begin{eqnarray}\displaystyle X=\left(\sqrt{2\hat{{\it\eta}}+u^{2}}-u\right)D_{-1+(\text{i}\hat{{\it\eta}})/2}(-u\text{e}^{-(\text{i}{\rm\pi})/4}),\quad Y=-2\text{e}^{(\text{i}{\rm\pi})/4}D_{(\text{i}\hat{{\it\eta}})/2}(-u\text{e}^{-(\text{i}{\rm\pi})/4}), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

where $D$ is the parabolic cylinder function,

(2.8a,b ) $$\begin{eqnarray}\displaystyle u=\sqrt{\frac{2}{|e|E_{0}}}(p_{\Vert }+eE_{0}t)\quad \text{and}\quad \hat{{\it\eta}}=\frac{m^{2}+p_{\bot }^{2}}{|e|E_{0}}. & & \displaystyle\end{eqnarray}$$

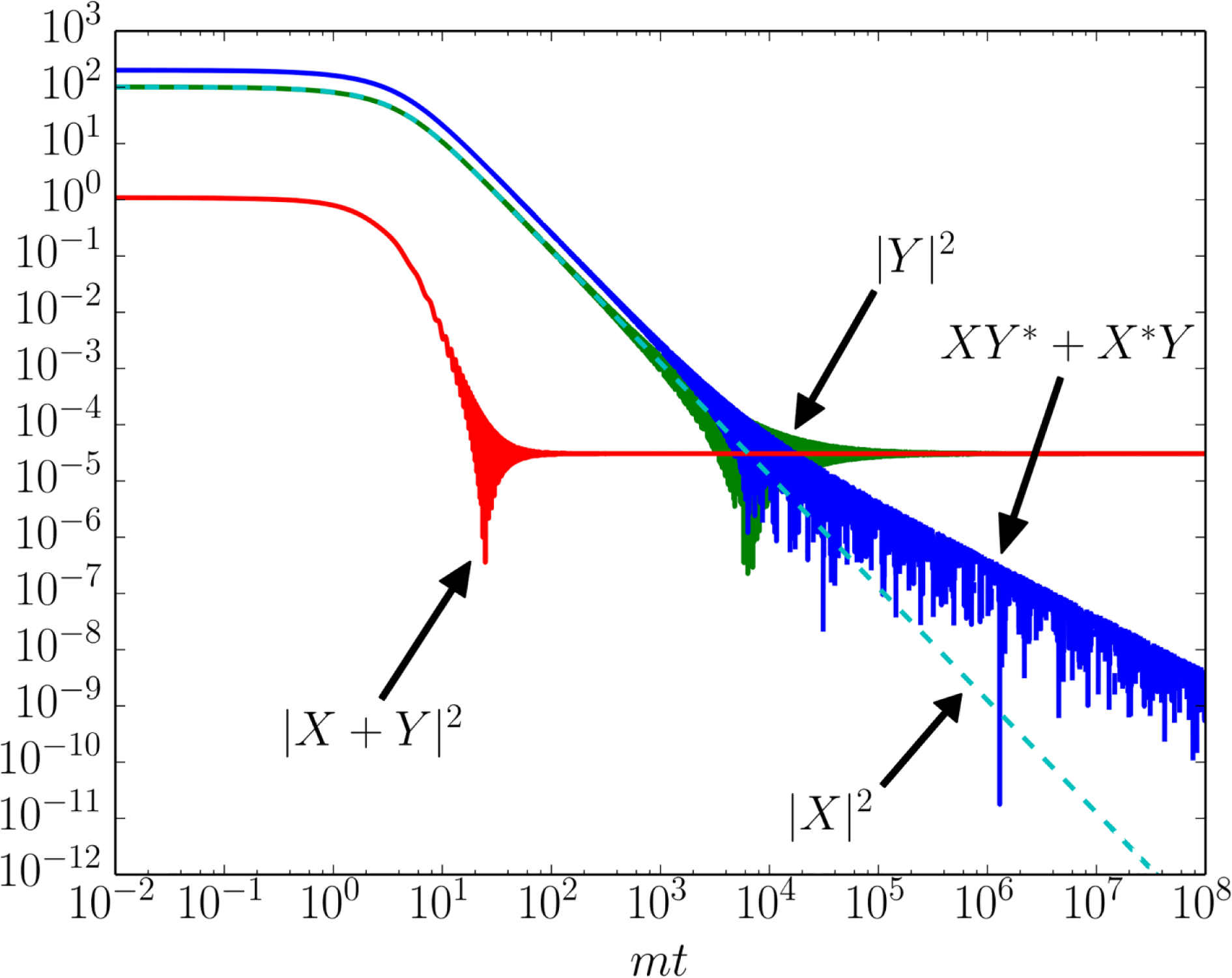
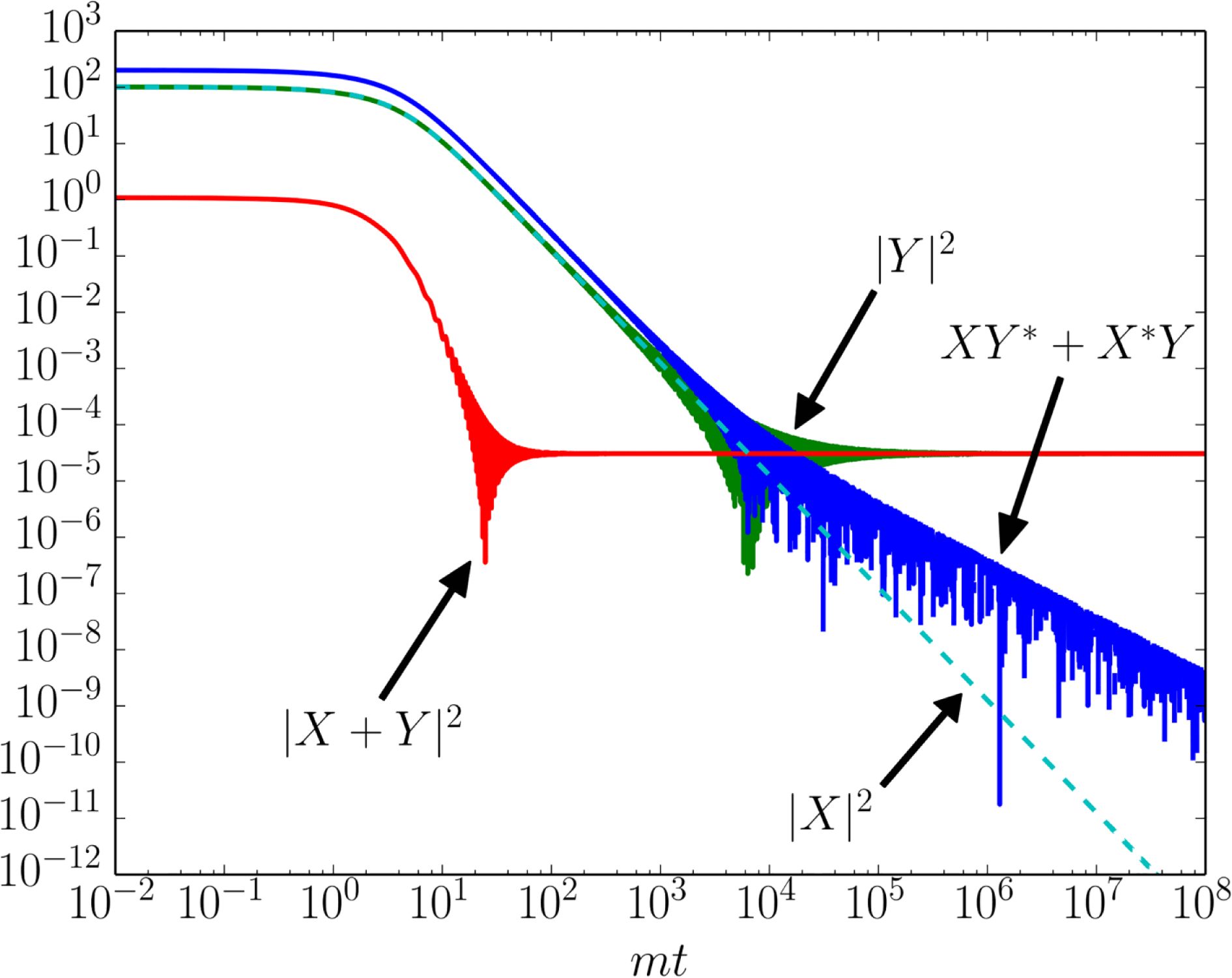
While for $E=0.2E_{c}$ the net function $\propto |X+Y|^{2}$ has already reached its asymptotic value at $tm\approx 20$ (see figure 3), the individual components $|X|^{2}$ , $|Y|^{2}$ and $XY^{\ast }+X^{\ast }Y$ display a violent time dependence on much longer times. Note also the subtle cancellations.

In the case of the Sauter pulse, see figure 2, the asymptotic values of $f$ are reached at shorter times with decreasing values of ${\it\tau}$ . The relatively large values of $f\;(t\approx 0)$ have sometimes tempted researchers to relate them to particular effects caused by the transient state. Clearly, only observables, e.g. those provided by probe beams, at asymptotic times are reliable. It is questionable, however, whether such probes can disentangle transient state contributions and asymptotic state contributions in a unique manner.

Figure 3. Time evolution of the components defined in (2.7) of the analytical solution (2.6) of the Schwinger case depicted for $E_{0}=0.2E_{c}$ . Cyan dashed curve: $|X|^{2}$ , green curve: $|Y|^{2}$ , blue curve: interference term $XY^{\ast }+X^{\ast }Y$ , red curve: $|X+Y|^{2}$ .

3 Laser-assisted Breit–Wheeler process

The laser-assisted, nonlinear Breit–Wheeler process (cf. Jansen & Müller Reference Jansen and Müller2013, Reference Jansen and Müller2016; Krajewska & Kaminski Reference Krajewska and Kaminski2014; Wu & Xue Reference Wu and Xue2014; Meuren et al. Reference Meuren, Hatsagortsyan, Keitel and Di Piazza2015) is dealt with within the strong-field QED (Furry picture) as reaction ${\it\gamma}^{\prime }\rightarrow e_{A}^{+}+e_{A}^{-}$ where $e_{A}^{\pm }$ denote dressed electron/positron states as Volkov solutions of the Dirac equation in a plane wave model with vector potential of the common classical background field

(3.1) $$\begin{eqnarray}A^{{\it\mu}}({\it\phi})={\it\gamma}_{X}^{-1}f_{X}({\it\phi}){\it\varepsilon}_{X}^{{\it\mu}}\cos {\it\phi}+{\it\gamma}_{L}^{-1}f_{L}({\it\eta}{\it\phi}){\it\varepsilon}_{L}^{{\it\mu}}\cos {\it\eta}{\it\phi},\end{eqnarray}$$

where the polarization four-vectors are ${\it\varepsilon}_{X,L}^{{\it\mu}}$ and the above-defined Keldysh parameters ${\it\gamma}_{1,2}$ have been transposed to ${\it\gamma}_{X,L}$ ; ${\it\gamma}^{\prime }$ denotes the high-energy probe photon traversing the field (3.1). The XFEL (frequency ${\it\omega}$ ) and laser (frequency ${\it\eta}{\it\omega}$ , we assume in the following ${\it\eta}\ll 1$ ) beams are co-propagating and their linear polarizations are set perpendicular to each other to simplify the cumbersome numerical evaluation. Both are pulsed as described, for the sake of computational convenience, by the envelope functions $f_{X}=\exp \{-{\it\phi}^{2}/(2{\it\tau}_{X}^{2})\}$ and $f_{L}=\cos ^{2}({\rm\pi}{\it\phi}/(2{\it\tau}_{L}))$ for $-{\it\tau}_{L}\leqslant {\it\phi}\leqslant +{\it\tau}_{L}$ and zero elsewhere for the latter pulse shape. In contrast to (2.2) we treat here a somewhat more realistic case with different pulse durations ${\it\tau}_{X}$ and ${\it\tau}_{L}$ . The invariant phase is ${\it\phi}=k\cdot x$ with the dot indicating the scalar product of the four-wave vector $k$ and the space–time coordinate $x$ . It is convenient to parameterize the produced positron’s phase space by the following three variables: (i) the momentum exchange parameter $\ell$ , (ii) the azimuthal angle ${\it\varphi}$ with respect to the polarization direction of the assisting laser field; and (iii) the shifted rapidity $z=\log (p_{+}^{+}/p_{+}^{-})/2+\log ((1+{\it\eta}\ell ){\it\omega}_{X}/{\it\omega}_{X^{\prime }})/2$ . The energy-momentum balance for laser-assisted pair production can be put into the form $k_{X^{\prime }}^{{\it\mu}}+k_{X}^{{\it\mu}}+\ell k_{L}^{{\it\mu}}=p_{+}^{{\it\mu}}+p_{-}^{{\it\mu}}$ ( ${\it\mu}$ is a Lorentz index, as above), where $\ell$ represents here a hitherto unspecified momentum exchange between the assisting laser field $L$ and the produced pair. We define light-front coordinates, e.g. $x^{\pm }=x^{0}\pm x^{3}$ and $\boldsymbol{x}_{\bot }=(x_{1},x_{2})$ and analogously the light front components of four-momenta of the probe photon $X^{\prime }$ , the XFEL photon $X$ , the laser beam photons $L$ and the positron (subscript $+$ ) and electron (subscript $-$ ). They become handy because the laser four-momentum vectors only have one non-vanishing light-front component $k_{X,L}^{-}=2{\it\omega}_{X,L}$ . In particular, the energy-momentum balance contains the three conservation equations in light-front coordinates $k_{X^{\prime }}^{+}=p_{+}^{+}+p_{-}^{+}$ and $\boldsymbol{p}_{+}^{\bot }=-\boldsymbol{p}_{-}^{\bot }$ . Moreover, the knowledge of all particle momenta makes it possible to calculate $\ell$ via the fourth equation $\ell =((p_{+}^{-}+p_{-}^{-}-k_{X^{\prime }}^{-})/(k_{X}^{-}-1)/{\it\eta})$ . Treating $(\ell ,z,{\it\varphi})$ as independent variables the positron’s four-momenta are completely determined by the above energy-momentum balance equations (see Nousch et al. (Reference Nousch, Seipt, Kämpfer and Titov2016) for details, in particular for expressing the positron and electron momenta $p_{\pm }$ by $(\ell ,z,{\it\varphi})$ ).

Figure 4. Spectra for the laser-assisted Breit–Wheeler process for a probe photon of energy 60 MeV colliding head-on with an XFEL photon (energy 6 keV) and a co-propagating laser beam (frequency 10 eV). Further parameters are ${\it\eta}=1/600$ , ${\it\gamma}_{X}=10^{5}$ , ${\it\tau}_{X}=7{\it\tau}/(4{\rm\pi}{\it\eta})$ , ${\it\gamma}_{L}=2$ and ${\it\tau}_{L}=8{\rm\pi}$ in the field (3.1). These parameters translate into intensities of $6.2\times 10^{15}~\text{W}~\text{cm}^{-2}$ and $4.3\times 10^{19}~\text{W}~\text{cm}^{-2}$ for the XFEL and the laser, respectively. (a) Values of $\text{d}{\it\sigma}/\text{d}\ell \,\text{d}z\,\text{d}{\it\varphi}$ at $z=0$ and ${\it\varphi}={\rm\pi}$ as a function of $\ell$ (lower axis; the corresponding values of $p_{\bot }$ are given on the upper axis). The calculated spectrum is smoothed by a Gaussian window function with width ${\it\delta}=1.3$ to get the red curve. (b) Smoothed spectrum separately. (c) Phase ${\it\phi}$ as a function of $\ell$ (see Nousch et al. (Reference Nousch, Seipt, Kämpfer and Titov2016) for details). The vertical dotted lines depict the positions of diverging $\text{d}{\it\phi}/\text{d}\ell$ , where two branches of ${\it\phi}(\ell )$ merge.

Figure 5. As in figure 4(b) but for ${\it\gamma}_{L}=10$ , laser intensity $1.7\times 10^{18}~\text{W}~\text{cm}^{-2}$ (a) and ${\it\gamma}_{L}=1$ , laser intensity $1.7\times 10^{20}~\text{W}~\text{cm}^{-2}$ (b).

The theoretical basis for formulating and evaluating the cross-section is outlined in Nousch et al. (Reference Nousch, Seipt, Kämpfer and Titov2016). An example is displayed in figure 4(a) for ${\it\eta}=1/600$ , ${\it\gamma}_{X}=10^{5}$ , ${\it\tau}_{X}=7{\it\tau}/(4{\rm\pi}{\it\eta})$ , ${\it\gamma}_{L}=2$ and ${\it\tau}_{L}=8{\rm\pi}$ (examples for other parameters are exhibited in Nousch et al. (Reference Nousch, Seipt, Kämpfer and Titov2016)) for kinematical conditions, where the linear Breit–Wheeler effect for $X^{\prime }+X$ is just above the threshold. The involved spectral distribution (note that without the laser assistance only the Breit–Wheeler peak centred at $\ell =0$ corresponding to $p_{\bot }=0.62~\text{m}$ would appear with a finite width as a consequence of the finite x-ray pulse duration; cf. Titov et al. (Reference Titov, Takabe, Kämpfer and Hosaka2012, Reference Titov, Kämpfer, Takabe and Hosaka2013) and Nousch et al. (Reference Nousch, Seipt, Kämpfer and Titov2012) for an enhancement of pair production in short laser pulses). The spectrum can be smoothed by a window function with a resolution scale of ${\it\delta}=1.3$ (which is an ad hoc choice to better show the strength distribution and which may be considered as a simple account for finite energy resolution respective $p_{\bot }$ distribution) resulting in the red curve which is exhibited separately in (b). In line with the interpretation in Seipt et al. (Reference Seipt, Surzhykov, Fritzsche and Kämpfer2016) and Nousch et al. (Reference Nousch, Seipt, Kämpfer and Titov2016) the prominent peaks are caustics related to stationary phase points determined by the turning points of the invariant phase ${\it\phi}$ as a function of the variable $\ell$ , see figure 4(c). This interpretation implies that the total cross-section may be approximately factorized into a plain Breit–Wheeler production part and a final-state interaction part, where the latter means the redistribution of the produced particles by the impact of the laser field. An analogue interpretation of particle production in constant cross-field approximation in very strong fields has been put forward in Meuren, Keitel & Di Piazza (Reference Meuren, Keitel and Di Piazza2016). Figure 5 demonstrates the strong impact of the laser field intensity. For smaller values of ${\it\gamma}_{L}$ , the transverse momentum spectrum becomes more stretched and its shape is changed. This challenges the observability of the peaks related to caustics in multi-shot experiments with fluctuating laser intensities. In fact, for the unfavourable case of equally weighted deviations, a window of less than 20 % is required to keep the peak structures, see figure 6. A truncated Gaussian distribution with $1{\it\sigma}$ width in the same interval is, of course, much more favourable for keeping the peaks, in particular for larger $p_{\bot }$ . We consider here only one particular case of the laser-assisted, linear Breit–Wheeler process which turns into the textbook Breit–Wheeler process upon switching off the laser. Nonlinearities with reference to the XFEL beam, subthreshold (with reference to the $X^{\prime }$ + XFEL kinematics) effects combined with larger laser intensities, carrier envelope phase effects and a wider range of kinematical parameters (e.g. ${\it\omega}_{L}=O$ (1 eV)) need to be explored as well to arrive at a complete picture. Among the yet to be analysed issues in terms of an experimental proposal are non-monochromaticity and misalignment disturbances.

Figure 6. As in figure 4(b) but variation of ${\it\gamma}_{L}$ around ${\it\gamma}_{L}=2$ . (a) ${\it\gamma}_{L}=2.22$ , (b) ${\it\gamma}_{L}=1.82$ , (c) superposition of smoothed spectra for ${\it\gamma}_{L}=1.88\ldots 2.12$ corresponding to the laser intensity parameter $a_{0}={\it\gamma}_{L}^{-1}=0.5\pm 0.03$ .

4 Summary

In summary we have supplied further important details of (i) the amplification effect of the assisted dynamical Schwinger effect, and (ii) the phase space redistribution in the laser-assisted Breit–Wheeler process. Both topics are motivated by the availability of x-rays by XFELs and upcoming ultra-high intensity laser beams. We consider the perspectives offered by the combination of both beam types resulting in bi-frequent fields. Concerning the Schwinger-related investigations we find that significant pair production by the dynamical assistance requires much higher frequencies than those provided by XFEL beams in conjunction with future ELI-IV field intensities. The crucial challenge for the laser-assisted Breit–Wheeler process and an access to the predicted caustic structures is the high-energy probe photon beam in combination with dedicated phase space selective detector set-ups. The bi-frequent fields are dealt with as a classical background. An avenue for further work is the proper account of quantum fluctuations and a unifying description of counter- and co-propagating fields.