1. Introduction
Future tokamak-based fusion power plants and experimental devices towards this goal (e.g. the ITER; Tomabechi et al. Reference Tomabechi, Gilleland, Sokolov and Toschi1991) are expected to operate at steady state with a substantial non-inductive current fraction (Gormezano et al. Reference Gormezano2007), which generally renders a reversed shear scenario (Huang et al. Reference Huang2020). In this circumstance, the reversed shear Alfvén eigenmode (RSAE; also known as Alfvén cascade) is frequently observed (Sharapov et al. Reference Sharapov, Testa, Alper, Borba, Fasoli, Hawkes, Heeter, Mantsinen and Hellermann2001) as driven unstable by energetic particles (EPs) (Zonca et al. Reference Zonca, Briguglio, Chen, Dettrick, Fogaccia, Testa and Vlad2002; Fasoli et al. Reference Fasoli, Gormenzano, Berk, Breizman, Briguglio, Darrow, Gorelenkov, Heidbrink, Jaun, Konovalov, Nazikian, Noterdaeme, Sharapov, Shinohara, Testa, Tobita, Todo, Vlad and Zonca2007; Chen et al. Reference Chen2014; Chen & Zonca Reference Chen and Zonca2016) in present-day tokamaks, and is expected to play significant roles in future reactors (Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018), in transporting fusion alpha particles to the tokamak edge (Wang et al. Reference Wang, Wang, Briguglio, Qiu, Vlad and Zonca2019), which has deleterious effects on plasma self-heating, and may damage the plasma-facing components (Ding et al. Reference Ding, Pitts, Borodin, Carpentier, Ding, Gong, Guo, Kirschner, Kocan, Li, Luo, Mao, Qian, Stangeby, Wampler, Wang and Wang2015). The RSAE is a branch of the shear Alfvén wave (SAW) eigenmode localized radially near the minimum of the safety factor $q$![]() -profile (Sharapov et al. Reference Sharapov, Alper, Berk, Borba, Breizman, Challis, Fasoli, Hawkes, Hender, Mailloux, Pinches and Testa2002), which is denoted as $q_{\min }$
-profile (Sharapov et al. Reference Sharapov, Alper, Berk, Borba, Breizman, Challis, Fasoli, Hawkes, Hender, Mailloux, Pinches and Testa2002), which is denoted as $q_{\min }$![]() . The lowest-order RSAE frequency in the incompressible limit, $\omega \simeq k_{\parallel }v_{A}\simeq |n-m/q_{\min }|v_{A}/R$
. The lowest-order RSAE frequency in the incompressible limit, $\omega \simeq k_{\parallel }v_{A}\simeq |n-m/q_{\min }|v_{A}/R$![]() , reflects the sensitive dependence on the instantaneous $q_{\min }$
, reflects the sensitive dependence on the instantaneous $q_{\min }$![]() value for given toroidal/poloidal mode numbers $n$
value for given toroidal/poloidal mode numbers $n$![]() /$m$
/$m$![]() , and this feature can be used in $q$
, and this feature can be used in $q$![]() -profile measurement, i.e. magnetohydrodynamic (MHD) spectroscopy (Fasoli et al. Reference Fasoli, Testa, Sharapov, Berk, Breizman, Gondhalekar, Heeter and Mantsinen2002; Chen et al. Reference Chen2014). Here, $k_{\parallel }$
-profile measurement, i.e. magnetohydrodynamic (MHD) spectroscopy (Fasoli et al. Reference Fasoli, Testa, Sharapov, Berk, Breizman, Gondhalekar, Heeter and Mantsinen2002; Chen et al. Reference Chen2014). Here, $k_{\parallel }$![]() is the wavenumber parallel to the equilibrium magnetic field $\boldsymbol B$
is the wavenumber parallel to the equilibrium magnetic field $\boldsymbol B$![]() , $v_{A}$
, $v_{A}$![]() is the Alfvén speed and $R$
is the Alfvén speed and $R$![]() is the major radius. Typically, RSAEs are dominated by one or two poloidal harmonics, with the radial width $\propto \sqrt {q/(r^{2}_{0}q'')}$
is the major radius. Typically, RSAEs are dominated by one or two poloidal harmonics, with the radial width $\propto \sqrt {q/(r^{2}_{0}q'')}$![]() (see section III of Zonca et al. (Reference Zonca, Briguglio, Chen, Dettrick, Fogaccia, Testa and Vlad2002)) with $r_{0}$
(see section III of Zonca et al. (Reference Zonca, Briguglio, Chen, Dettrick, Fogaccia, Testa and Vlad2002)) with $r_{0}$![]() being the radial location of $q_{\min }$
being the radial location of $q_{\min }$![]() and $q''\equiv \partial ^2_{r}q$
and $q''\equiv \partial ^2_{r}q$![]() . Despite the fairly good understanding of the linear physics, the nonlinear dynamics of RSAE is still interesting and valuable to research, especially in view of the EP as well as thermal particle transport induced by the associated electromagnetic field perturbations (Wang et al. Reference Wang, Wang, Briguglio, Qiu, Vlad and Zonca2019, Reference Wang, Qiu, Zonca, Briguglio and Vlad2020; Shi et al. Reference Shi, Qiu, Chen, Wang, Shi, Yu, Yang, Zhong, Jiang, Ji, Yang, Xu and Duan2020; Wei et al. Reference Wei, Wang, Shi, Chen, Chen and Qiu2021). The transport rate is closely related to the perturbation amplitude (Chen Reference Chen1999; Zonca et al. Reference Zonca, Chen, Falessi and Qiu2021); and in reactor-relevant cases with many SAWs simultaneously driven unstable by EPs, the EP orbit could become chaotic and eventually lost in the presence of many low-amplitude SAWs (threshold value $\delta B/B\sim {O}(10^{-4})$
. Despite the fairly good understanding of the linear physics, the nonlinear dynamics of RSAE is still interesting and valuable to research, especially in view of the EP as well as thermal particle transport induced by the associated electromagnetic field perturbations (Wang et al. Reference Wang, Wang, Briguglio, Qiu, Vlad and Zonca2019, Reference Wang, Qiu, Zonca, Briguglio and Vlad2020; Shi et al. Reference Shi, Qiu, Chen, Wang, Shi, Yu, Yang, Zhong, Jiang, Ji, Yang, Xu and Duan2020; Wei et al. Reference Wei, Wang, Shi, Chen, Chen and Qiu2021). The transport rate is closely related to the perturbation amplitude (Chen Reference Chen1999; Zonca et al. Reference Zonca, Chen, Falessi and Qiu2021); and in reactor-relevant cases with many SAWs simultaneously driven unstable by EPs, the EP orbit could become chaotic and eventually lost in the presence of many low-amplitude SAWs (threshold value $\delta B/B\sim {O}(10^{-4})$![]() ) (White et al. Reference White, Gorelenkov, Heidbrink and Zeeland2010a,Reference White, Gorelenkov, Heidbrink and Zeelandb). Thus, the assessment of the nonlinear RSAE saturation mechanism and amplitude plays a crucial role in evaluating the operation scenario and the EP confinement property.
) (White et al. Reference White, Gorelenkov, Heidbrink and Zeeland2010a,Reference White, Gorelenkov, Heidbrink and Zeelandb). Thus, the assessment of the nonlinear RSAE saturation mechanism and amplitude plays a crucial role in evaluating the operation scenario and the EP confinement property.
In general, the channels of SAW nonlinear saturation can be classified into two routes, namely wave–particle nonlinear interactions and wave–wave nonlinear couplings (Berk & Breizman Reference Berk and Breizman1990; Chen & Zonca Reference Chen and Zonca2013, Reference Chen and Zonca2016; Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Vlad and Wang2015). The former focuses on the perturbation to the resonant EP phase-space distribution function by finite-amplitude SAWs (Berk & Breizman Reference Berk and Breizman1990; Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Vlad and Wang2015), and has been widely investigated using numerical simulations, as reviewed in Chen & Zonca (Reference Chen and Zonca2016) and Lauber (Reference Lauber2013). By contrast, the latter is relatively less explored. Most previous analytical works considered the toroidal Alfvén eigenmode (TAE) (Cheng, Chen & Chance Reference Cheng, Chen and Chance1985) as a paradigm case, including saturation via ion-induced scattering (Hahm & Chen Reference Hahm and Chen1995; Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2019a), nonlinear modification to the SAW continuum structure (Zonca et al. Reference Zonca, Romanelli, Vlad and Kar1995; Chen et al. Reference Chen, Zonca, Santoro and Hu1998), the spontaneous generation of zero-frequency zonal structures (ZFZS) (Chen & Zonca Reference Chen and Zonca2012; Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2016a, Reference Qiu, Chen and Zonca2017) as well as geodesic acoustic mode (Qiu et al. Reference Qiu, Chen, Zonca and Chen2018a, Reference Qiu, Chen, Zonca and Chen2019b). Since the RSAEs are expected to be prevalent in future steady-state burning plasmas, RSAE saturation via wave–wave nonlinearity deserves special attention. In particular, the toroidally symmetric zonal field structures (Zonca et al. Reference Zonca, Chen, Falessi and Qiu2021), including the ZFZS, are well known to play important roles in regulating drift wave turbulences (Lin et al. Reference Lin, Hahm, Lee, Tang and White1998; Hahm et al. Reference Hahm, Beer, Lin, Hammett, Lee and Tang1999; Chen, Lin & White Reference Chen, Lin and White2000; Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005) including drift Alfvén waves, and thus leading to cross-scale couplings (Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Milovanov, Qiu, Vlad and Wang2015a) and nonlinear saturation via scattering of drift waves to the short-radial-wavelength regime (or shearing in some literature). In this work, spontaneous ZFZS excitation by RSAE modulational instability is analysed using nonlinear gyrokinetic theory.
As noted above, the spontaneous excitation of ZFZS by TAE is discussed in Chen & Zonca (Reference Chen and Zonca2012). It is shown that under certain conditions, the zonal current (ZC) is preferentially excited over the electrostatic zonal flow (ZF), with the branch ratio of ZF/ZC excitation determined by various geometry effects, including the breaking of pure Alfvénic state by toroidicity and neoclassical shielding of ZF (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998). In contrast to the TAE case, it is shown in Qiu, Chen & Zonca (Reference Qiu, Chen and Zonca2016b) that for beta-induced Alfvén eigenmode (BAE), the excitation of ZF generally dominates, due to the $|k_{\parallel }v_{A}/\omega |\ll 1$![]() ordering. For the case of RSAE analysed herein, its frequency is sensitively determined by the value of $q_{\min }$
ordering. For the case of RSAE analysed herein, its frequency is sensitively determined by the value of $q_{\min }$![]() and the underlying values of toroidal/poloidal mode numbers $n$
and the underlying values of toroidal/poloidal mode numbers $n$![]() /$m$
/$m$![]() , and generally sweeps between the typical BAE to TAE frequency ranges. It is shown that depending on the specific plasma parameters including $k_{\parallel }$
, and generally sweeps between the typical BAE to TAE frequency ranges. It is shown that depending on the specific plasma parameters including $k_{\parallel }$![]() , both ZC and ZF generation may dominate, and the previous conclusions on TAE (Chen & Zonca Reference Chen and Zonca2012) and BAE (Qiu et al. Reference Qiu, Chen and Zonca2016b) can be recovered as limiting cases of the general nonlinear dispersion relation derived without assuming specific plasma parameters.
, both ZC and ZF generation may dominate, and the previous conclusions on TAE (Chen & Zonca Reference Chen and Zonca2012) and BAE (Qiu et al. Reference Qiu, Chen and Zonca2016b) can be recovered as limiting cases of the general nonlinear dispersion relation derived without assuming specific plasma parameters.
We note that several nonlinear processes, with comparable cross-sections, may be comparably important in saturating Alfvén eigenmode, as addressed in Qiu et al. (Reference Qiu, Chen, Zonca and Chen2018b). In particular, a channel unique for RSAE saturation is proposed in this work. Due to the ZC and the associated perturbed poloidal magnetic field generation, the $q$![]() -profile is modulated, which leads to the modification of the local SAW continuum in the vicinity of $q_{\min }$
-profile is modulated, which leads to the modification of the local SAW continuum in the vicinity of $q_{\min }$![]() , and consequently to RSAE saturation. The relevance of this channel to RSAE nonlinear saturation is analysed and evaluated.
, and consequently to RSAE saturation. The relevance of this channel to RSAE nonlinear saturation is analysed and evaluated.
This remainder of this paper is arranged as follows. In § 2, the theoretical model is given. In § 3, the general nonlinear equations describing RSAE evolution and ZFZS excitation are derived. Section 4 is devoted to a study of the linear growth stage of the modulational instability; and the nonlinear saturation of RSAE via ZFZS scattering is investigated in § 5. Finally, brief conclusion and discussion are given in § 6.
2. Theoretical model
The nonlinear evolution of this system is studied using the standard nonlinear perturbation theory, considering a shifted circular tokamak equilibrium described by a set of field-aligned flux coordinates $(r, \theta , \varphi )$![]() . The perturbed fields are represented by two field variables, namely the electrostatic potential $\delta \phi$
. The perturbed fields are represented by two field variables, namely the electrostatic potential $\delta \phi$![]() and the parallel component of vector potential $\delta A_{\parallel }$
and the parallel component of vector potential $\delta A_{\parallel }$![]() , while the parallel magnetic field fluctuation $\delta B_{\parallel }$
, while the parallel magnetic field fluctuation $\delta B_{\parallel }$![]() is suppressed, consistent with $\beta \ll 1$
is suppressed, consistent with $\beta \ll 1$![]() ordering of typical laboratory plasmas. Here, $\beta$
ordering of typical laboratory plasmas. Here, $\beta$![]() is the ratio of thermal to magnetic pressures. For convenience, $\delta A_{\parallel }$
is the ratio of thermal to magnetic pressures. For convenience, $\delta A_{\parallel }$![]() is replaced by $\delta \psi \equiv \omega \delta A_{\parallel }/(ck_{\parallel })$
is replaced by $\delta \psi \equiv \omega \delta A_{\parallel }/(ck_{\parallel })$![]() , such that the ideal MHD limit, i.e. vanishing parallel electric field fluctuation $\delta E_{\parallel }$
, such that the ideal MHD limit, i.e. vanishing parallel electric field fluctuation $\delta E_{\parallel }$![]() , corresponds to simply $\delta \phi =\delta \psi$
, corresponds to simply $\delta \phi =\delta \psi$![]() . In this work, it is assumed that the RSAE is excited by a source outside this nonlinear system, such as EPs, and the nonlinear coupling is dominated by bulk plasma contribution. For the cases with EPs contributing significantly to nonlinear ZFZS generation (Todo, Berk & Breizman Reference Todo, Berk and Breizman2010; Biancalani et al. Reference Biancalani, Bottino, Lauber, Mishchenko and Vannini2020), interested readers may refer to Qiu et al. (Reference Qiu, Chen and Zonca2016a, Reference Qiu, Chen and Zonca2017) for more systematic discussions. To start with, we consider the two-field coupled system which consists of a RSAE (subscript ‘R’) and ZFZS (subscript ‘Z’), i.e. $\delta \phi =\delta \phi _{R}+\delta \phi _{Z}$
. In this work, it is assumed that the RSAE is excited by a source outside this nonlinear system, such as EPs, and the nonlinear coupling is dominated by bulk plasma contribution. For the cases with EPs contributing significantly to nonlinear ZFZS generation (Todo, Berk & Breizman Reference Todo, Berk and Breizman2010; Biancalani et al. Reference Biancalani, Bottino, Lauber, Mishchenko and Vannini2020), interested readers may refer to Qiu et al. (Reference Qiu, Chen and Zonca2016a, Reference Qiu, Chen and Zonca2017) for more systematic discussions. To start with, we consider the two-field coupled system which consists of a RSAE (subscript ‘R’) and ZFZS (subscript ‘Z’), i.e. $\delta \phi =\delta \phi _{R}+\delta \phi _{Z}$![]() with $\delta \phi _{R}=\delta \phi _{0}+\delta \phi _{0^{*}}$
with $\delta \phi _{R}=\delta \phi _{0}+\delta \phi _{0^{*}}$![]() . Here, $\delta \phi _{0}$
. Here, $\delta \phi _{0}$![]() represents the RSAE with positive real frequency and $\delta \phi _{0^{*}}$
represents the RSAE with positive real frequency and $\delta \phi _{0^{*}}$![]() represents the counterpart with negative real frequency, of which there may be a rich spectrum of different radial eigenstates.
represents the counterpart with negative real frequency, of which there may be a rich spectrum of different radial eigenstates.
Considering the reactor-relevant parameter regime with $nq\gg 1$![]() , the ballooning mode representation (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978) for theRSAE is adopted:
, the ballooning mode representation (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978) for theRSAE is adopted:
Here, $m=m_{0}+j$![]() with $m_{0}$
with $m_{0}$![]() being the reference poloidal mode number, $x\equiv nq-m_{0}$
being the reference poloidal mode number, $x\equiv nq-m_{0}$![]() , $\varPhi _{0}$
, $\varPhi _{0}$![]() is the parallel mode structure with typical radial extension comparable to the distance between neighbouring mode rational surfaces, $A_{0}$
is the parallel mode structure with typical radial extension comparable to the distance between neighbouring mode rational surfaces, $A_{0}$![]() is the mode envelope amplitude and $\hat {k}_{r,0}$
is the mode envelope amplitude and $\hat {k}_{r,0}$![]() is the radial envelope wavenumber accounting for the slowly varying radial structures. Note that the RSAE is typically characterized by one dominant poloidal harmonic, while multiple sub-dominant poloidal harmonics exist due to toroidicity. Furthermore, $\int |\varPhi _{0}|^{2}{\textrm {d}\kern0.06em x}=1$
is the radial envelope wavenumber accounting for the slowly varying radial structures. Note that the RSAE is typically characterized by one dominant poloidal harmonic, while multiple sub-dominant poloidal harmonics exist due to toroidicity. Furthermore, $\int |\varPhi _{0}|^{2}{\textrm {d}\kern0.06em x}=1$![]() is used as normalization condition.
is used as normalization condition.
Consequently, the ZFZS is expected to have a fine radial structure in addition to the well-known mesoscale structure (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005), as a result of the RSAE fine radial mode structure highly localized around $q_{\min }$![]() . For ZFZS dominated by $n=0, m=0$
. For ZFZS dominated by $n=0, m=0$![]() scalar potential perturbation (Chen et al. Reference Chen, Lin and White2000), we take
scalar potential perturbation (Chen et al. Reference Chen, Lin and White2000), we take
with $\varPhi _{Z}$![]() accounting for the fine radial structure (Qiu et al. Reference Qiu, Chen and Zonca2016b) due to nonlinear mode coupling and $A_{Z}\exp {\textrm {i}\int \hat {k}_{Z}\, \textrm {d} r}$
accounting for the fine radial structure (Qiu et al. Reference Qiu, Chen and Zonca2016b) due to nonlinear mode coupling and $A_{Z}\exp {\textrm {i}\int \hat {k}_{Z}\, \textrm {d} r}$![]() being the well-known mesoscale structure. This general representation adopted here can be applied to recover the results obtained from the linear growth stage of the modulational instability, by separating the RSAE into pump and upper/lower sidebands, as often used in previous work (Chen et al. Reference Chen, Lin and White2000); and is also recovered in § 4, from the derived general nonlinear equations.
being the well-known mesoscale structure. This general representation adopted here can be applied to recover the results obtained from the linear growth stage of the modulational instability, by separating the RSAE into pump and upper/lower sidebands, as often used in previous work (Chen et al. Reference Chen, Lin and White2000); and is also recovered in § 4, from the derived general nonlinear equations.
The governing equations describing the nonlinear processes can be derived from the quasi-neutrality condition
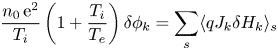
and the nonlinear gyrokinetic vorticity equation derived from parallel Ampère's law (Chen & Zonca Reference Chen and Zonca2016)
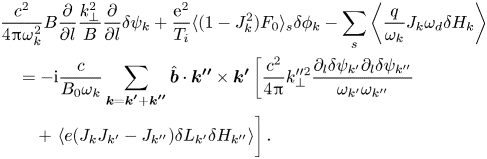
Here, $J_{k}\equiv J_{0}(k_{\perp }\rho )$![]() with $J_{0}$
with $J_{0}$![]() being the Bessel function of zero index accounting for finite Larmor radius effects, $\rho =v_{\perp }/\varOmega _{c}$
being the Bessel function of zero index accounting for finite Larmor radius effects, $\rho =v_{\perp }/\varOmega _{c}$![]() is the Larmor radius with $\varOmega _{c}$
is the Larmor radius with $\varOmega _{c}$![]() being the cyclotron frequency, $F_{0}$
being the cyclotron frequency, $F_{0}$![]() is the equilibrium particle distribution function, $\omega _{d}=(v_{\perp }^{2}+2v_{\parallel }^{2})(k_{r}\sin \theta +k_{\theta }\cos \theta )/(2\varOmega _{c}R)$
is the equilibrium particle distribution function, $\omega _{d}=(v_{\perp }^{2}+2v_{\parallel }^{2})(k_{r}\sin \theta +k_{\theta }\cos \theta )/(2\varOmega _{c}R)$![]() is the magnetic drift frequency, $l$
is the magnetic drift frequency, $l$![]() is the length along the equilibrium magnetic field line, $\langle \cdots \rangle$
is the length along the equilibrium magnetic field line, $\langle \cdots \rangle$![]() means velocity space integration, $\sum _{s}$
means velocity space integration, $\sum _{s}$![]() is the summation of different particle species with $s=i, e$
is the summation of different particle species with $s=i, e$![]() representing ion and electron, and $\delta L_{k}\equiv \delta \phi _{k}-k_{\parallel }v_{\parallel }\delta \psi _{k}/\omega _{k}$
representing ion and electron, and $\delta L_{k}\equiv \delta \phi _{k}-k_{\parallel }v_{\parallel }\delta \psi _{k}/\omega _{k}$![]() . The three terms on the left-hand side of (2.4) are, respectively, the field line bending, inertial and curvature coupling terms, dominating the linear SAW physics. The two terms on the right-hand side of (2.4) correspond to Maxwell and Reynolds stresses (Chen et al. Reference Chen, Lin, White and Zonca2001) that contribute to nonlinear mode couplings as Maxwell and Reynolds stresses do not cancel each other, with their contribution dominating in the radially fast-varying inertial layer (Chen et al. Reference Chen, Lin and White2000), and $\sum _{\boldsymbol {k}=\boldsymbol {k'}+\boldsymbol {k''}}$
. The three terms on the left-hand side of (2.4) are, respectively, the field line bending, inertial and curvature coupling terms, dominating the linear SAW physics. The two terms on the right-hand side of (2.4) correspond to Maxwell and Reynolds stresses (Chen et al. Reference Chen, Lin, White and Zonca2001) that contribute to nonlinear mode couplings as Maxwell and Reynolds stresses do not cancel each other, with their contribution dominating in the radially fast-varying inertial layer (Chen et al. Reference Chen, Lin and White2000), and $\sum _{\boldsymbol {k}=\boldsymbol {k'}+\boldsymbol {k''}}$![]() indicates the wavenumber and frequency matching condition required for nonlinear mode coupling. Here $\delta H_{k}$
indicates the wavenumber and frequency matching condition required for nonlinear mode coupling. Here $\delta H_{k}$![]() is the non-adiabatic particle response, which can be derived from the nonlinear gyrokinetic equation (Frieman & Chen Reference Frieman and Chen1982):
is the non-adiabatic particle response, which can be derived from the nonlinear gyrokinetic equation (Frieman & Chen Reference Frieman and Chen1982):
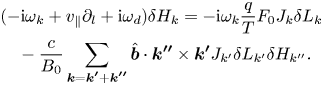
For RSAE with $|k_{\parallel }v_{e}|\gg |\omega _k|\gg |k_{\parallel }v_{i}|, |\omega _{d}|$![]() , the linear ion/electron responses can be derived to leading order as $\delta H^{L}_{k, i}=eF_{0}J_k\delta \phi _ k/T_{i}$
, the linear ion/electron responses can be derived to leading order as $\delta H^{L}_{k, i}=eF_{0}J_k\delta \phi _ k/T_{i}$![]() and $\delta H^{L}_{k,e}=-eF_{0}\delta \psi _{k}/T_{e}$
and $\delta H^{L}_{k,e}=-eF_{0}\delta \psi _{k}/T_{e}$![]() . Furthermore, one can have that, to leading order, the ideal MHD constraint is satisfied, i.e. $\delta \phi _{R}=\delta \psi _{R}$
. Furthermore, one can have that, to leading order, the ideal MHD constraint is satisfied, i.e. $\delta \phi _{R}=\delta \psi _{R}$![]() , by substituting the ion/electron responses of the RSAE into the quasi-neutrality condition.
, by substituting the ion/electron responses of the RSAE into the quasi-neutrality condition.
On the other hand, considering such a nonlinear system dominated by SAW instabilities, we can also use the parallel component of the nonlinear ideal Ohm's law as an alternative to (2.3):
with $\delta \boldsymbol {u}$![]() being the $\boldsymbol {E}\times \boldsymbol {B}$
being the $\boldsymbol {E}\times \boldsymbol {B}$![]() drift velocity. We note that (2.6) is equivalent to (2.3), ignoring the high-order ${O}(k_{\perp }^{2}\rho _{i}^{2})$
drift velocity. We note that (2.6) is equivalent to (2.3), ignoring the high-order ${O}(k_{\perp }^{2}\rho _{i}^{2})$![]() corrections.
corrections.
3. General nonlinear equations
In this section, the general nonlinear equations describing the self-consistent RSAE evolution are derived, including the generation of ZFZS and the feedback modulation of RSAE by ZFZS. Generally speaking, the nonlinear process can be divided into two stages, i.e. linear growth stage and strongly nonlinear stage, determined by whether the modulation to the pump wave is small. The governing equations derived in this section, without separating the RSAE into pump wave and its sidebands, are general, and can be used for describing both stages as shown in later sections (Guo, Chen & Zonca Reference Guo, Chen and Zonca2009; Chen et al. Reference Chen, Wei, Wei and Qiu2021).
Considering the nonlinear coupling dominated by the radially fast-varying inertial region, one can obtain the equation describing the electrostatic ZF excitation from the surface-averaged vorticity equation as
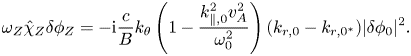
Here, $\hat {\chi }_{Z}=\chi _{Z}/(k_{Z}^{2}\rho _{i}^{2})\simeq 1.6q^{2}\epsilon ^{-1/2}$![]() with $\chi _{Z}$
with $\chi _{Z}$![]() being the well-known neoclassical shielding of ZFZS (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998) and $\epsilon \equiv r/R$
being the well-known neoclassical shielding of ZFZS (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998) and $\epsilon \equiv r/R$![]() being the inverse aspect ratio of the torus. One can note that $(k_{r,0}-k_{r,0^{*}})|\delta \varPhi _{0}|^{2}\equiv [(\hat {k}_{r,0}-\hat {k}_{r,0^{*}})-\textrm {i}(\partial _{r}\ln \varPhi _{0}- \partial _{r}\ln \varPhi _{0^{*}})]|\delta \varPhi _{0}|^{2}$
being the inverse aspect ratio of the torus. One can note that $(k_{r,0}-k_{r,0^{*}})|\delta \varPhi _{0}|^{2}\equiv [(\hat {k}_{r,0}-\hat {k}_{r,0^{*}})-\textrm {i}(\partial _{r}\ln \varPhi _{0}- \partial _{r}\ln \varPhi _{0^{*}})]|\delta \varPhi _{0}|^{2}$![]() is radial modulation with $(\hat {k}_{r,0}-\hat {k}_{r,0^{*}})$
is radial modulation with $(\hat {k}_{r,0}-\hat {k}_{r,0^{*}})$![]() denoting envelope modulation (Chen & Zonca Reference Chen and Zonca2012) and $(\partial _{r}\ln \varPhi _{0}-\partial _{r}\ln \varPhi _{0^{*}})$
denoting envelope modulation (Chen & Zonca Reference Chen and Zonca2012) and $(\partial _{r}\ln \varPhi _{0}-\partial _{r}\ln \varPhi _{0^{*}})$![]() denoting parallel mode structure evolution (Qiu et al. Reference Qiu, Chen and Zonca2016b), which gives the fine radial structure of ZFZS. For RSAE typically dominated by one or two poloidal harmonics, $(\partial _{r}\ln \varPhi _{0}-\partial _{r}\ln \varPhi _{0^{*}})$
denoting parallel mode structure evolution (Qiu et al. Reference Qiu, Chen and Zonca2016b), which gives the fine radial structure of ZFZS. For RSAE typically dominated by one or two poloidal harmonics, $(\partial _{r}\ln \varPhi _{0}-\partial _{r}\ln \varPhi _{0^{*}})$![]() is the dominant term, and determines the zonal structure radial wavenumber $k_{Z}=-\textrm {i}(\partial _{r} \ln \varPhi _{0}-\partial _{r}\ln \varPhi _{0^{*}})$
is the dominant term, and determines the zonal structure radial wavenumber $k_{Z}=-\textrm {i}(\partial _{r} \ln \varPhi _{0}-\partial _{r}\ln \varPhi _{0^{*}})$![]() , as addressed in Qiu et al. (Reference Qiu, Chen and Zonca2017).
, as addressed in Qiu et al. (Reference Qiu, Chen and Zonca2017).
The equation describing the electromagnetic ZC excitation can be derived from (2.6), considering $k_{\parallel ,Z}=0$![]() and noting $\delta \psi _{Z}\equiv \omega _{0}\delta A_{\parallel ,Z}/(ck_{\parallel ,0})$
and noting $\delta \psi _{Z}\equiv \omega _{0}\delta A_{\parallel ,Z}/(ck_{\parallel ,0})$![]() is defined using the frequency and parallel wavenumber of RSAE, as
is defined using the frequency and parallel wavenumber of RSAE, as
In deriving the (3.2), the ideal MHD condition for RSAE ($\delta \phi _{0}=\delta \psi _{0}$![]() ) is used, and $\partial _{r}\ln \delta \psi _{Z}=\partial _{r}\ln |\delta \phi _{0}|^{2}$
) is used, and $\partial _{r}\ln \delta \psi _{Z}=\partial _{r}\ln |\delta \phi _{0}|^{2}$![]() is noted.
is noted.
One can also derive the corresponding equations describing RSAE from (2.6) as
which describes the deviation from the ideal MHD constraint due to nonlinear ZFZS modulation. The other equation for RSAE can be derived from the nonlinear vorticity equation as
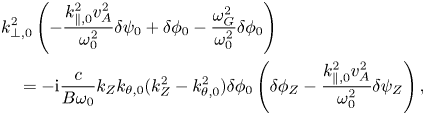
with the term proportional to $\delta \phi _{Z}$![]() on the right-hand side corresponding to Reynolds stress contribution and the $\delta \psi _{Z}$
on the right-hand side corresponding to Reynolds stress contribution and the $\delta \psi _{Z}$![]() term corresponding to Maxwell contribution. The third term on the left-hand side of (3.4) is the SAW continuum upshift due to geodesic-curvature-induced compression, and $\omega _{G}$
term corresponding to Maxwell contribution. The third term on the left-hand side of (3.4) is the SAW continuum upshift due to geodesic-curvature-induced compression, and $\omega _{G}$![]() is the frequency of geodesic acoustic mode (Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2009). Note that (3.1)–(3.4) are the general equations for ZFZS generation by SAW instabilities in the Wentzel–Kramer–Brillouin (WKB) limit, and have expression similar to that describing ZFZS generation by TAE, as derived in Qiu et al. (Reference Qiu, Chen and Zonca2017), except the coefficient of the $\delta \psi$
is the frequency of geodesic acoustic mode (Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2009). Note that (3.1)–(3.4) are the general equations for ZFZS generation by SAW instabilities in the Wentzel–Kramer–Brillouin (WKB) limit, and have expression similar to that describing ZFZS generation by TAE, as derived in Qiu et al. (Reference Qiu, Chen and Zonca2017), except the coefficient of the $\delta \psi$![]() term on the right-hand side of (3.4), where $k^2_{\parallel } v^2_{A}/\omega ^2\simeq 1$
term on the right-hand side of (3.4), where $k^2_{\parallel } v^2_{A}/\omega ^2\simeq 1$![]() is applied for TAE. However, the RSAE frequency is sensitively determined by $k_{\parallel }$
is applied for TAE. However, the RSAE frequency is sensitively determined by $k_{\parallel }$![]() through $q_{\min }$
through $q_{\min }$![]() , and is between the BAE and TAE frequency ranges, so a more general expression is derived here for ZFZS generation by RSAE. However, though with similar WKB expressions of dispersion relation, the physics underlying the ZFZS generation by RSAE is very different from that of the TAE case, as is embedded in the $k_{\parallel }$
, and is between the BAE and TAE frequency ranges, so a more general expression is derived here for ZFZS generation by RSAE. However, though with similar WKB expressions of dispersion relation, the physics underlying the ZFZS generation by RSAE is very different from that of the TAE case, as is embedded in the $k_{\parallel }$![]() term that determines the relative importance of various terms, for example, whether ZF or ZC generation should be dominated.
term that determines the relative importance of various terms, for example, whether ZF or ZC generation should be dominated.
Substituting (3.3) into (3.4), one then obtains the equation describing the modulation of RSAE by ZFZS:
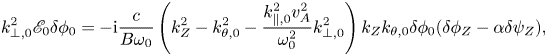
with $\mathscr {E}_0$![]() being the RSAE dispersion relation and $\alpha \equiv (k_{\parallel ,0}^{2}v_{A}^{2}/\omega _{0}^{2})(-2k_{\theta , 0}^{2})/(k_{Z}^{2}-k_{\theta ,0}^{2}-k_{\parallel ,0}^{2}v_{A}^{2} k_{\perp ,0}^{2}/\omega _{0}^{2})$
being the RSAE dispersion relation and $\alpha \equiv (k_{\parallel ,0}^{2}v_{A}^{2}/\omega _{0}^{2})(-2k_{\theta , 0}^{2})/(k_{Z}^{2}-k_{\theta ,0}^{2}-k_{\parallel ,0}^{2}v_{A}^{2} k_{\perp ,0}^{2}/\omega _{0}^{2})$![]() . Equation (3.5) is general, and can be reduced to various limits depending on different plasma parameters, through the value of $\alpha$
. Equation (3.5) is general, and can be reduced to various limits depending on different plasma parameters, through the value of $\alpha$![]() dependence on $k_{\parallel ,0}$
dependence on $k_{\parallel ,0}$![]() ; e.g. the mode dynamics described by (3.5) is similar to the TAE case with $(k_{\parallel ,0}^{2}v_{A}^{2}/\omega _{0}^{2})\sim {O}(1)$
; e.g. the mode dynamics described by (3.5) is similar to the TAE case with $(k_{\parallel ,0}^{2}v_{A}^{2}/\omega _{0}^{2})\sim {O}(1)$![]() , and $|k_{\parallel ,0}|\simeq 1/(2qR)$
, and $|k_{\parallel ,0}|\simeq 1/(2qR)$![]() , and thus $\alpha \simeq 1$
, and thus $\alpha \simeq 1$![]() . On the other hand, the mode behaviour gets close to a BAE with $k_{\parallel ,0}\simeq 0$
. On the other hand, the mode behaviour gets close to a BAE with $k_{\parallel ,0}\simeq 0$![]() , and thus $\alpha \simeq 0$
, and thus $\alpha \simeq 0$![]() . For simplicity of investigation, the RSAE WKB dispersion relation can be adopted here as $\mathscr {E}_{0}\simeq (1-k_{\parallel ,0}^{2}v_{A}^{2}/\omega _{0}^{2}- \omega _{G}^{2}/\omega _{0}^{2})$
. For simplicity of investigation, the RSAE WKB dispersion relation can be adopted here as $\mathscr {E}_{0}\simeq (1-k_{\parallel ,0}^{2}v_{A}^{2}/\omega _{0}^{2}- \omega _{G}^{2}/\omega _{0}^{2})$![]() , while the radial global dispersion relation (Zonca et al. Reference Zonca, Briguglio, Chen, Dettrick, Fogaccia, Testa and Vlad2002) can be applied for more quantitative analysis.
, while the radial global dispersion relation (Zonca et al. Reference Zonca, Briguglio, Chen, Dettrick, Fogaccia, Testa and Vlad2002) can be applied for more quantitative analysis.
Furthermore, subtracting (3.1) by $\alpha \times$![]() (3.2), one can obtain
(3.2), one can obtain
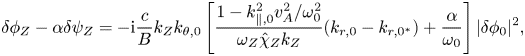
which can be substituted into (3.5), and yield the general equation describing the self-modulation of RSAE as
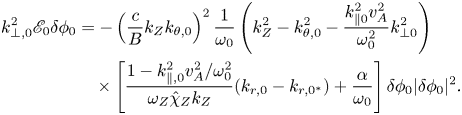
Both ZF and ZC generation by RSAE are systematically accounted for in (3.7) on the same footing, with the first term in square brackets corresponding to ZF generation and the second term to ZC. On the one hand, which one is preferentially excited is addressed in § 4. On the other hand, ZFZS generation can lead to RSAE saturation by scattering it to linearly stable radial eigenstates. The nonlinear saturation level can be determined by self-consistently solving (3.7) as a nonlinear Schrödinger equation (Chen et al. Reference Chen, Wei, Wei and Qiu2021), while a rough estimation is given in, for example, Qiu et al. (Reference Qiu, Chen, Zonca and Chen2018a), by separating the RSAE into a pump and its sidebands, and deriving the fixed-point solution of the coupled nonlinear equations. Since RSAE linear properties are very sensitive to the $q$![]() -profile, the modulation of the$q$
-profile, the modulation of the$q$![]() -profile caused by the nonlinearly generated ZC may have a great impact on RSAE nonlinear saturation. This is discussed in § 5.
-profile caused by the nonlinearly generated ZC may have a great impact on RSAE nonlinear saturation. This is discussed in § 5.
4. Spontaneous excitation of ZFZS by RSAE via modulational instability
To investigate the linear growth stage of the modulational instability, we follow the analysis of Chen & Zonca (Reference Chen and Zonca2012), and consider the fluctuation consisting of a constant-amplitude pump wave $\varOmega _{P}\equiv \varOmega _{P}(\omega _{P}, \boldsymbol {k}_{P})$![]() and its upper and lower sidebands $\varOmega _{\pm }\equiv \varOmega _{\pm }(\omega _{\pm }, \boldsymbol {k}_{\pm })$
and its upper and lower sidebands $\varOmega _{\pm }\equiv \varOmega _{\pm }(\omega _{\pm }, \boldsymbol {k}_{\pm })$![]() due to the modulation of the ZFZS $\varOmega _{Z}\equiv \varOmega _{Z}(\omega _{Z}, \boldsymbol {k}_{Z})$
due to the modulation of the ZFZS $\varOmega _{Z}\equiv \varOmega _{Z}(\omega _{Z}, \boldsymbol {k}_{Z})$![]() (Chen et al. Reference Chen, Lin and White2000). Here, subscripts ‘$P$
(Chen et al. Reference Chen, Lin and White2000). Here, subscripts ‘$P$![]() ’, ‘$+$
’, ‘$+$![]() ’ and ‘$-$
’ and ‘$-$![]() ’ denote RSAE pump, upper sideband and lower sideband, respectively, with $\delta \phi _{0}=\delta \phi _{P}+\delta \phi _{+}$
’ denote RSAE pump, upper sideband and lower sideband, respectively, with $\delta \phi _{0}=\delta \phi _{P}+\delta \phi _{+}$![]() , $\delta \phi _{0^{*}}=\delta \phi _{P^{*}}+\delta \phi _{-}$
, $\delta \phi _{0^{*}}=\delta \phi _{P^{*}}+\delta \phi _{-}$![]() , and
, and
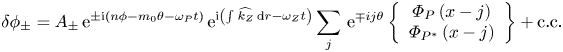
Then the general nonlinear equations (3.1)–(3.4) can be reduced to equations describing $\delta \phi _{Z}$![]() , $\delta \phi _{+}$
, $\delta \phi _{+}$![]() and $\delta \phi _{-}$
and $\delta \phi _{-}$![]() generation by the fixed-amplitude pump RSAE, while the feedback of ZFZS and RSAE sidebands to the pump wave is neglected, focusing on the initial stage of the nonlinear process. Considering the frequency/wavenumber matching condition ($\omega _{\pm }=\pm \omega _{P}+\omega _{Z}$
generation by the fixed-amplitude pump RSAE, while the feedback of ZFZS and RSAE sidebands to the pump wave is neglected, focusing on the initial stage of the nonlinear process. Considering the frequency/wavenumber matching condition ($\omega _{\pm }=\pm \omega _{P}+\omega _{Z}$![]() , $\boldsymbol {k}_{\pm }=\pm \boldsymbol {k}_{P}+\boldsymbol {k}_{Z}$
, $\boldsymbol {k}_{\pm }=\pm \boldsymbol {k}_{P}+\boldsymbol {k}_{Z}$![]() ) embedded in the above expressions, equation (3.1) can be reduced to
) embedded in the above expressions, equation (3.1) can be reduced to
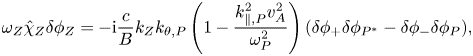
with $(1-k^{2}_{\parallel ,P}v^{2}_{A}/\omega ^{2}_{P})$![]() representing the competition of Reynolds and Maxwell stresses in breaking the pure Alfvénic state (Chen & Zonca Reference Chen and Zonca2012, Reference Chen and Zonca2013). On the other hand, (3.2) describing ZC excitation can be reduced to
representing the competition of Reynolds and Maxwell stresses in breaking the pure Alfvénic state (Chen & Zonca Reference Chen and Zonca2012, Reference Chen and Zonca2013). On the other hand, (3.2) describing ZC excitation can be reduced to
The nonlinear equation describing RSAE sideband generation through the ZFZS modulation to pump RSAE can be derived from (3.5) as
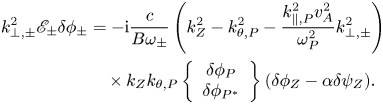
Equations (4.3)–(4.5) are equivalent to (34)–(36) for TAE cases as derived in Qiu et al. (Reference Qiu, Chen and Zonca2017), with the coefficient $\alpha$![]() generalized to include a broader parameter regime ($\alpha \simeq 1$
generalized to include a broader parameter regime ($\alpha \simeq 1$![]() for TAE as discussed in Qiu et al. (Reference Qiu, Chen and Zonca2017)). Note that $k_{\perp ,\pm }^{2}=k_{\perp ,P}^{2}+k_{Z}^{2}$
for TAE as discussed in Qiu et al. (Reference Qiu, Chen and Zonca2017)). Note that $k_{\perp ,\pm }^{2}=k_{\perp ,P}^{2}+k_{Z}^{2}$![]() and $k_{\perp ,+}^{2}$
and $k_{\perp ,+}^{2}$![]() are used in the derivation later. Similarly, subtracting (4.3) by $\alpha \times$
are used in the derivation later. Similarly, subtracting (4.3) by $\alpha \times$![]() (4.4), one can obtain
(4.4), one can obtain
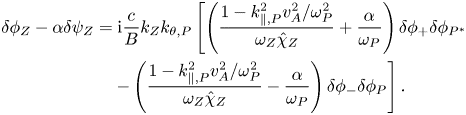
The modulational instability dispersion relation can then be derived by substituting (4.5) into (4.6) as
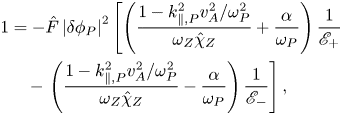
with $\hat {F}=(ck_{Z}k_{\theta ,P}/B)^{2}(-k_{Z}^{2}+k_{\theta ,P}^{2} +k_{\parallel ,P}^{2}v_{A}^{2}k_{\perp ,+}^{2}/\omega _{P}^{2})/(\omega _{P}k_{\perp ,+}^{2})$![]() being a nonlinear coupling coefficient. Furthermore, considering that RSAE sidebands still obey the dispersion relation of RSAE by $\mathscr {E}_{\pm }=\mathscr {E}_{0}(\omega _Z\pm \omega _P, k_{Z})$
being a nonlinear coupling coefficient. Furthermore, considering that RSAE sidebands still obey the dispersion relation of RSAE by $\mathscr {E}_{\pm }=\mathscr {E}_{0}(\omega _Z\pm \omega _P, k_{Z})$![]() , one can expand $\mathscr {E}_{\pm }$
, one can expand $\mathscr {E}_{\pm }$![]() along the RSAE characteristics, as $\mathscr {E}_{\pm }\simeq (\partial \mathscr {E}_{0}/\partial \omega _{0})(\pm \omega _{Z}-\varDelta )$
along the RSAE characteristics, as $\mathscr {E}_{\pm }\simeq (\partial \mathscr {E}_{0}/\partial \omega _{0})(\pm \omega _{Z}-\varDelta )$![]() with $\varDelta \equiv -k_{Z}^{2}(\partial ^{2}\mathscr {E}_{0}/\partial k_{r}^{2})/(2\partial \mathscr {E}_{0}/\partial \omega _{0})$
with $\varDelta \equiv -k_{Z}^{2}(\partial ^{2}\mathscr {E}_{0}/\partial k_{r}^{2})/(2\partial \mathscr {E}_{0}/\partial \omega _{0})$![]() being the frequency mismatch, describing the frequency shift of RSAE sidebands from the pump RSAE dispersion relation due to the ZFZS modulation. Denoting $\gamma \equiv -\textrm {i}\omega _{Z}$
being the frequency mismatch, describing the frequency shift of RSAE sidebands from the pump RSAE dispersion relation due to the ZFZS modulation. Denoting $\gamma \equiv -\textrm {i}\omega _{Z}$![]() and noting $\omega _{\pm }\simeq \pm \omega _{P}$
and noting $\omega _{\pm }\simeq \pm \omega _{P}$![]() , the modulational instability dispersion relation can be written as
, the modulational instability dispersion relation can be written as
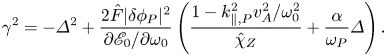
The first term on the right-hand side of (4.8) is the threshold condition due to frequency mismatch and the second term represents the nonlinear drive. Thus, the ZFZS can be spontaneously excited when the nonlinear drive overcomes the threshold condition due to frequency mismatch, as the RSAE amplitude is large enough, or the nonlinear coupling is strong enough, as we address in the following discussion. Furthermore, the first term in parentheses corresponds to the ZF contribution to the nonlinear coupling, and the second term corresponds to ZC. For the ZF contribution, there are two restrictions due to, first, the partial cancellation of Reynolds and Maxwell stresses with the ‘residual’ drive due to deviation from the ideal MHD limit due to plasma non-uniformity (reversed $q$![]() -profile here) that breaks the pure Alfvénic state (Zonca et al. Reference Zonca, Briguglio, Chen, Dettrick, Fogaccia, Testa and Vlad2002; Chen & Zonca Reference Chen and Zonca2013), and second, the neoclassical shielding of ZF as shown by $\hat {\chi }_{Z}$
-profile here) that breaks the pure Alfvénic state (Zonca et al. Reference Zonca, Briguglio, Chen, Dettrick, Fogaccia, Testa and Vlad2002; Chen & Zonca Reference Chen and Zonca2013), and second, the neoclassical shielding of ZF as shown by $\hat {\chi }_{Z}$![]() in the denominator, with $\hat {\chi }_{Z}\sim q^{2}/\epsilon$
in the denominator, with $\hat {\chi }_{Z}\sim q^{2}/\epsilon$![]() , which is typically much larger than unity (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Chen & Zonca Reference Chen and Zonca2016).
, which is typically much larger than unity (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998; Chen & Zonca Reference Chen and Zonca2016).
For the ZC contribution, there are also two important factors that crucially determine the nonlinear process, with the first being the sign of $\varDelta$![]() , which is typically determined by specific plasma parameters. The ZC term is a driving term for $\varDelta >0$
, which is typically determined by specific plasma parameters. The ZC term is a driving term for $\varDelta >0$![]() ; while for $\varDelta <0$
; while for $\varDelta <0$![]() , the ZC term becomes a damping term for this nonlinear process; and then the condition for modulational instability becomes very stringent, with additional requirement for the ZF term being dominant over the ZC term, which is not easy to satisfy due to the two restrictions as addressed in the paragraph above. The other important factor is the value of $\alpha$
, the ZC term becomes a damping term for this nonlinear process; and then the condition for modulational instability becomes very stringent, with additional requirement for the ZF term being dominant over the ZC term, which is not easy to satisfy due to the two restrictions as addressed in the paragraph above. The other important factor is the value of $\alpha$![]() . As noted before, if RSAE localizes near the rational surface, $\alpha \simeq 0$
. As noted before, if RSAE localizes near the rational surface, $\alpha \simeq 0$![]() because of $k_{\parallel }\simeq 0$
because of $k_{\parallel }\simeq 0$![]() , meaning that ZC generation is very weak and is similar to the BAE case investigated in Qiu et al. (Reference Qiu, Chen and Zonca2016b); on the other hand, if RSAE localizes in the middle of two neighbouring rational surfaces, $\alpha \simeq 1$
, meaning that ZC generation is very weak and is similar to the BAE case investigated in Qiu et al. (Reference Qiu, Chen and Zonca2016b); on the other hand, if RSAE localizes in the middle of two neighbouring rational surfaces, $\alpha \simeq 1$![]() , and this case is similar to the TAE case (Chen & Zonca Reference Chen and Zonca2012) with ZC generation preferred. So for RSAE, with $k_{\parallel }$
, and this case is similar to the TAE case (Chen & Zonca Reference Chen and Zonca2012) with ZC generation preferred. So for RSAE, with $k_{\parallel }$![]() and its frequency determined by $q_{\min }$
and its frequency determined by $q_{\min }$![]() and the corresponding mode numbers, both ZF and ZC generation could be dominant, depending on the specific plasma parameters, and should be investigated case by case. Furthermore, the threshold amplitude can be roughly estimated in two limit cases, e.g. as RSAE frequency approaches TAE and BAE frequencies, as $\delta B_{\theta }/B \sim {O}(10^{-4})$
and the corresponding mode numbers, both ZF and ZC generation could be dominant, depending on the specific plasma parameters, and should be investigated case by case. Furthermore, the threshold amplitude can be roughly estimated in two limit cases, e.g. as RSAE frequency approaches TAE and BAE frequencies, as $\delta B_{\theta }/B \sim {O}(10^{-4})$![]() (Chen & Zonca Reference Chen and Zonca2012; Qiu et al. Reference Qiu, Chen and Zonca2016b).
(Chen & Zonca Reference Chen and Zonca2012; Qiu et al. Reference Qiu, Chen and Zonca2016b).
5. Nonlinear RSAE saturation
In strongly nonlinear stage, the feedback of ZFZS and RSAE sidebands to the pump wave can no longer be neglected, as the sideband amplitudes become comparable to that of the pump wave. It is indicated in (3.7) that ZS can play self-regulatory roles in RSAE nonlinear evolution by scattering the RSAE into short-radial-wavelength stable domains, which may lead to RSAE saturation. The saturation level can be derived from the coupled pump wave and sideband equations, as is shown in, for example, Zonca & Chen (Reference Zonca and Chen2008). In addition, another related channel unique for RSAE nonlinear saturation may exist, due to the modulation to the SAW continuum (Zonca et al. Reference Zonca, Romanelli, Vlad and Kar1995; Chen et al. Reference Chen, Zonca, Santoro and Hu1998) by the nonlinearly generated ZS (among which ZC plays a dominant role), considering the sensitive dependence of RSAE on SAW continuum accumulation point (for a visualization of RSAE physics dependence on $q_{\min }$![]() , interested readers may refer to Wang et al. (Reference Wang, Qiu, Zonca, Briguglio and Vlad2020) and figure 3 therein). The nonlinearly generated ZC is a toroidal current sharply localized around $q_{\min }$
, interested readers may refer to Wang et al. (Reference Wang, Qiu, Zonca, Briguglio and Vlad2020) and figure 3 therein). The nonlinearly generated ZC is a toroidal current sharply localized around $q_{\min }$![]() , which can generate a perturbed poloidal magnetic field and further modulate the $q$
, which can generate a perturbed poloidal magnetic field and further modulate the $q$![]() -profile and thus the SAW continuum near $q_{\min }$
-profile and thus the SAW continuum near $q_{\min }$![]() . Thus, one can reasonably speculate that the ZC plays an important role in RSAE saturation by modifying the equilibrium continuum, similar to the mechanism investigated in Zonca et al. (Reference Zonca, Romanelli, Vlad and Kar1995) and Chen et al. (Reference Chen, Zonca, Santoro and Hu1998) for TAE.
. Thus, one can reasonably speculate that the ZC plays an important role in RSAE saturation by modifying the equilibrium continuum, similar to the mechanism investigated in Zonca et al. (Reference Zonca, Romanelli, Vlad and Kar1995) and Chen et al. (Reference Chen, Zonca, Santoro and Hu1998) for TAE.
Here, consistent with the above speculation on the crucial role played by the ZC, we consider a simplified case that ZC generation is dominant. This assumption is natural for scenarios with $(k_{\parallel ,0}^{2}v_{A}^{2}/\omega _{0}^{2})\sim {O}(1)$![]() ; however, it may also be important for other parameter regimes for the reasons addressed above. Thus, (3.7) can be simplified as
; however, it may also be important for other parameter regimes for the reasons addressed above. Thus, (3.7) can be simplified as
Taking a two-scale analysis by assuming $\omega _{R}=\omega _{0}+\textrm {i}\partial _{\tau }$![]() , and expanding $\mathscr {E}_{0}\simeq (\partial \mathscr {E}_{0}/\partial \omega _{0})(\textrm {i}\partial _{\tau }-\textrm {i}\gamma ^{L}_{R}-\varDelta )$
, and expanding $\mathscr {E}_{0}\simeq (\partial \mathscr {E}_{0}/\partial \omega _{0})(\textrm {i}\partial _{\tau }-\textrm {i}\gamma ^{L}_{R}-\varDelta )$![]() with $\varDelta$
with $\varDelta$![]() being the nonlinearity-induced frequency shift and $\gamma ^{L}_{R}$
being the nonlinearity-induced frequency shift and $\gamma ^{L}_{R}$![]() the linear RSAE growth rate,Footnote 1 (5.1) becomes
the linear RSAE growth rate,Footnote 1 (5.1) becomes
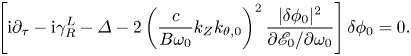
Equation (5.2) describes the RSAE nonlinear evolution due to scattering to different radial eigenstates (denoted by $\varDelta$![]() ) with different linear growth/damping rates ($\gamma ^{L}_{R}$
) with different linear growth/damping rates ($\gamma ^{L}_{R}$![]() ) and nonlinear self-modulation by ZC generation, and the saturation level can be estimated by balancing the frequency shift (Max($|\gamma ^{L}_{R}|$
) and nonlinear self-modulation by ZC generation, and the saturation level can be estimated by balancing the frequency shift (Max($|\gamma ^{L}_{R}|$![]() , $|\varDelta |$
, $|\varDelta |$![]() )) and the nonlinear RSAE modulation by the ZC. Then one has
)) and the nonlinear RSAE modulation by the ZC. Then one has
Equation (5.3) describes the RSAE saturation level due to scattering by self-generated ZC to neighbouring (linearly stabler) radial eigenstates, assuming $\varDelta \gg \gamma ^{L}_{R}$![]() . Cases with $\varDelta \ll \gamma ^{L}_{R}$
. Cases with $\varDelta \ll \gamma ^{L}_{R}$![]() can be evaluated similarly. The RSAE saturation level can be estimated by substituting typical parameters into the expression. Furthermore, (5.3) can be substituted into (3.2), and the saturation level of the perturbed poloidal magnetic field $\delta B_{\theta }$
can be evaluated similarly. The RSAE saturation level can be estimated by substituting typical parameters into the expression. Furthermore, (5.3) can be substituted into (3.2), and the saturation level of the perturbed poloidal magnetic field $\delta B_{\theta }$![]() can be estimated as
can be estimated as
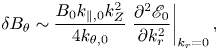
resulting in a modulation of local $q_{\min }$![]() by
by
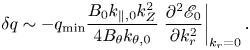
In deriving (5.4) and (5.5), we have noted $\delta \psi =\omega \delta A_{\parallel }/(ck_{\parallel })$![]() and $\boldsymbol {\delta B}=\nabla \times \delta A_{\parallel }\boldsymbol {b}$
and $\boldsymbol {\delta B}=\nabla \times \delta A_{\parallel }\boldsymbol {b}$![]() . Typical parameters can be adopted, i.e. $q_{\min }\sim {O}(1)$
. Typical parameters can be adopted, i.e. $q_{\min }\sim {O}(1)$![]() , $B_{0}/B_{\theta }\sim qR/r_{0}$
, $B_{0}/B_{\theta }\sim qR/r_{0}$![]() , $k_{\parallel }\sim 1/(qR)$
, $k_{\parallel }\sim 1/(qR)$![]() , $k_{\theta ,0}\rho _{d}\sim {O}(1)$
, $k_{\theta ,0}\rho _{d}\sim {O}(1)$![]() with $\rho _{d}$
with $\rho _{d}$![]() being the EP drift orbit radius and
being the EP drift orbit radius and
which can be reasonably assumed as $\sim {O}(0.1)$![]() . Thus, one can roughly estimate that $\delta B_{\theta }/B \sim {O}(10^{-4})$
. Thus, one can roughly estimate that $\delta B_{\theta }/B \sim {O}(10^{-4})$![]() as saturation amplitude and $\delta q/q\sim {O}(10^{-3})$
as saturation amplitude and $\delta q/q\sim {O}(10^{-3})$![]() . Such RSAE nonlinear saturation amplitude is equivalent to the estimation from the fixed-point solution in the driven-dissipative system described by three coupled equations such as (45)–(47) in Qiu et al. (Reference Qiu, Chen and Zonca2019a), and is in fact the same as the threshold amplitude on ZFZS nonlinear excitation. However, we note this is a rough order-of-magnitude estimation, since the nonlinear driven-dissipative system does not necessarily show a stationary saturation as described by the fixed-point solution. In fact, depending on the parameter regimes such as driving/dissipative rate and the initial conditions, the system may exhibit limit cycle oscillation, period doubling as well as route to chaos (Russell, Hanson & Ott Reference Russell, Hanson and Ott1980). Noting that the modification to local RSAE continuum frequency is $\sim O(n\delta qv_{A}/(qR))$
. Such RSAE nonlinear saturation amplitude is equivalent to the estimation from the fixed-point solution in the driven-dissipative system described by three coupled equations such as (45)–(47) in Qiu et al. (Reference Qiu, Chen and Zonca2019a), and is in fact the same as the threshold amplitude on ZFZS nonlinear excitation. However, we note this is a rough order-of-magnitude estimation, since the nonlinear driven-dissipative system does not necessarily show a stationary saturation as described by the fixed-point solution. In fact, depending on the parameter regimes such as driving/dissipative rate and the initial conditions, the system may exhibit limit cycle oscillation, period doubling as well as route to chaos (Russell, Hanson & Ott Reference Russell, Hanson and Ott1980). Noting that the modification to local RSAE continuum frequency is $\sim O(n\delta qv_{A}/(qR))$![]() and that for reactor burning plasma with $\rho _{d}/a\sim O(10^{-2})$
and that for reactor burning plasma with $\rho _{d}/a\sim O(10^{-2})$![]() most unstable RSAEs are characterized by $n\gtrsim O(10)$
most unstable RSAEs are characterized by $n\gtrsim O(10)$![]() (Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018), the modification to local SAW continuum is comparable to the RSAE linear growth rate $\gamma ^{L}_{R}$
(Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018), the modification to local SAW continuum is comparable to the RSAE linear growth rate $\gamma ^{L}_{R}$![]() or frequency differences between different radial eigenstates ($\sim \varDelta$
or frequency differences between different radial eigenstates ($\sim \varDelta$![]() ). Thus, one expects the ZC-induced SAW continuum modification in the vicinity of $q_{\min }$
). Thus, one expects the ZC-induced SAW continuum modification in the vicinity of $q_{\min }$![]() to play an important role in RSAE nonlinear saturation, though the self-consistent study analogous to Zonca et al. (Reference Zonca, Romanelli, Vlad and Kar1995) and Chen et al. (Reference Chen, Zonca, Santoro and Hu1998) is not presented. The systematic investigation of RSAE saturation due to nonlinear modification of SAW continuum and the resulting enhanced continuum damping will be presented in a separate publication.
to play an important role in RSAE nonlinear saturation, though the self-consistent study analogous to Zonca et al. (Reference Zonca, Romanelli, Vlad and Kar1995) and Chen et al. (Reference Chen, Zonca, Santoro and Hu1998) is not presented. The systematic investigation of RSAE saturation due to nonlinear modification of SAW continuum and the resulting enhanced continuum damping will be presented in a separate publication.
6. Conclusion and discussion
The general equations describing RSAE self-modulation via nonlinear excitation of ZFZS are derived using gyrokinetic theory, which is then applied to study the spontaneous ZFZS excitation via modulational instability as well as RSAE nonlinear saturation due to scattering to stabler radial eigenstates. It is found that both ZF and ZC can be dominant in the spontaneous excitation by RSAE, depending on the specific plasma parameters, especially $q_{\min }$![]() that determines the RSAE parallel wavenumber and frequency. The obtained general modulational instability dispersion relation for ZFZS excitation by RSAE, (4.8), can recover the results of TAE (Chen & Zonca Reference Chen and Zonca2012) and BAE (Qiu et al. Reference Qiu, Chen and Zonca2016b) in the proper limits, i.e. by taking $|k_{\parallel }v_{A}/\omega |\rightarrow 1$
that determines the RSAE parallel wavenumber and frequency. The obtained general modulational instability dispersion relation for ZFZS excitation by RSAE, (4.8), can recover the results of TAE (Chen & Zonca Reference Chen and Zonca2012) and BAE (Qiu et al. Reference Qiu, Chen and Zonca2016b) in the proper limits, i.e. by taking $|k_{\parallel }v_{A}/\omega |\rightarrow 1$![]() and $0$
and $0$![]() , respectively. The properties of ZFZS generation by RSAE, noting that the typical RSAE parallel wavenumber and frequency are between those of TAE and BAE, can be understood based on the knowledge obtained from TAE (Chen & Zonca Reference Chen and Zonca2012) and BAE (Qiu et al. Reference Qiu, Chen and Zonca2016b).
, respectively. The properties of ZFZS generation by RSAE, noting that the typical RSAE parallel wavenumber and frequency are between those of TAE and BAE, can be understood based on the knowledge obtained from TAE (Chen & Zonca Reference Chen and Zonca2012) and BAE (Qiu et al. Reference Qiu, Chen and Zonca2016b).
An interesting step forward is that the saturation level of RSAE is qualitatively estimated by balancing the nonlinear scattering by ZFZS with the frequency differences between different radial eigenstates ($\sim \varDelta$![]() ), assuming ZC playing a dominant role in RSAE scattering. The corresponding ZC saturation level as well as the modification to local $q_{\min }$
), assuming ZC playing a dominant role in RSAE scattering. The corresponding ZC saturation level as well as the modification to local $q_{\min }$![]() are also estimated. It is found that the resulting modification to local SAW continuum accumulation point frequency can be at least comparable to the RSAE linear growth rate or frequency mismatch between different radial eigenstates for burning plasma scenarios with most unstable RSAEs characterized by $n\gtrsim O(10)$
are also estimated. It is found that the resulting modification to local SAW continuum accumulation point frequency can be at least comparable to the RSAE linear growth rate or frequency mismatch between different radial eigenstates for burning plasma scenarios with most unstable RSAEs characterized by $n\gtrsim O(10)$![]() (Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018). Thus, the modification of local SAW continuum by ZC is expected to contribute significantly to RSAE saturation (Zonca et al. Reference Zonca, Romanelli, Vlad and Kar1995; Chen et al. Reference Chen, Zonca, Santoro and Hu1998). And it is natural to speculate that similar physical processes may happen in the regions sensitive to the magnetic field perturbation. For example, in the region near the X-point, one expects that ZC may also be driven by edge MHD modes such as the kinetic ballooning mode, and this may be important for the equilibrium and stability of a tokamak, and lead to, for example, vertical instability.
(Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018). Thus, the modification of local SAW continuum by ZC is expected to contribute significantly to RSAE saturation (Zonca et al. Reference Zonca, Romanelli, Vlad and Kar1995; Chen et al. Reference Chen, Zonca, Santoro and Hu1998). And it is natural to speculate that similar physical processes may happen in the regions sensitive to the magnetic field perturbation. For example, in the region near the X-point, one expects that ZC may also be driven by edge MHD modes such as the kinetic ballooning mode, and this may be important for the equilibrium and stability of a tokamak, and lead to, for example, vertical instability.
The above estimation based on (5.1), assuming dominant ZC generation by taking $|k_{\parallel }v_{A}/\omega |\sim 1$![]() , is valid for other parameter regimes due to the weak coupling coefficients of ZF generation, except for the cases where $q_{\min }$
, is valid for other parameter regimes due to the weak coupling coefficients of ZF generation, except for the cases where $q_{\min }$![]() is localized very close to a low-order rational surface, such that the RSAE properties are close to those of BAE with predominantly ZF generation (Qiu et al. Reference Qiu, Chen and Zonca2016b). The logic underlying the reasoning presented in § 5 is that the RSAE and ZFZS saturation levels are estimated without accounting for the modification to the SAW continuum, which is then used to estimate the modification to the SAW continuum by the saturated ZC, and it is found that the modification to the SAW continuum could be comparable to or even more important than the ZFZS shearing. Thus, the obtained results indicate that the modification to the SAW continuum will start to influence the RSAE nonlinear evolution, before it saturates due to self-modulation via ZFZS generation. Our work thus indicates that multiple processes may contribute comparably to the RSAE saturation, and should be accounted for on the same footing, based on the solid understanding of each individual process, to properly assess the saturation and thus EP transport by RSAE. This is of particular importance since RSAEs are expected to be strongly excited by core-localized fusion alphas in future reactors characterized by advanced reversed shear scenarios.
is localized very close to a low-order rational surface, such that the RSAE properties are close to those of BAE with predominantly ZF generation (Qiu et al. Reference Qiu, Chen and Zonca2016b). The logic underlying the reasoning presented in § 5 is that the RSAE and ZFZS saturation levels are estimated without accounting for the modification to the SAW continuum, which is then used to estimate the modification to the SAW continuum by the saturated ZC, and it is found that the modification to the SAW continuum could be comparable to or even more important than the ZFZS shearing. Thus, the obtained results indicate that the modification to the SAW continuum will start to influence the RSAE nonlinear evolution, before it saturates due to self-modulation via ZFZS generation. Our work thus indicates that multiple processes may contribute comparably to the RSAE saturation, and should be accounted for on the same footing, based on the solid understanding of each individual process, to properly assess the saturation and thus EP transport by RSAE. This is of particular importance since RSAEs are expected to be strongly excited by core-localized fusion alphas in future reactors characterized by advanced reversed shear scenarios.
Acknowledgements
The authors acknowledge Professor L. Chen (Zhejiang University, China and University of California, Irvine) and Dr F. Zonca (ENEA, Italy) for fruitful discussions.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
This work is supported by the National Key R&D Program of China (Z.Q., grant no. 2017YFE0301900) and the National Science Foundation of China (Z.Q., grant no. 11875233). Z.Q. is also supported by "Users of Excellence program of Hefei Science Center CAS unser Contract No. 2021HSC-UE016".
Declaration of interest
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.



