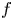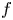1. Introduction
Plasma kinetic simulations are an essential tool in the study of weakly collisional/collisionless systems. Such conditions are realised in both astrophysical and laboratory plasmas. Collisions, either via binary Coulomb or frequent wave–particle interactions can be appropriately modelled with the aid of a Fokker–Planck approach (Chandrasekhar Reference Chandrasekhar1943). Thus treated, one arrives at the Vlasov–Fokker–Planck equation, which has the following form
Here, $f = f(t, \boldsymbol {r}, \boldsymbol {p})$![]() is the particle (number) density in the six-dimensional phase-space, or simply the distribution function. Here, $\boldsymbol {v}$
is the particle (number) density in the six-dimensional phase-space, or simply the distribution function. Here, $\boldsymbol {v}$![]() is the velocity of the particles with $\boldsymbol {F}$
is the velocity of the particles with $\boldsymbol {F}$![]() the force acting on them. The derivatives are taken with respect to the $\boldsymbol {r}$
the force acting on them. The derivatives are taken with respect to the $\boldsymbol {r}$![]() - and $\boldsymbol {p}$
- and $\boldsymbol {p}$![]() -coordinates. The right-hand side of the equation represents the effect of the particles’ interactions; ‘Sc’ stands for ‘scattering’.
-coordinates. The right-hand side of the equation represents the effect of the particles’ interactions; ‘Sc’ stands for ‘scattering’.
Several codes have been developed to solve the multi-dimensional Vlasov equation numerically (for example, von Alfthan et al. Reference von Alfthan, Pokhotelov, Kempf, Hoilijoki, Honkonen, Sandroos and Palmroth2014; Juno et al. Reference Juno, Hakim, TenBarge, Shi and Dorland2018). Simulations with this approach are expensive in multi-dimensions. When possible, it is pragmatic to exploit the fact that collisions tend to drive the distribution towards isotropy. A large body of work has exploited this fact to derive transport coefficients in ionized plasmas including Coulomb collisions, for example in the form of resistivity and conductivity tensors (e.g. Braginskii Reference Braginskii1965). Reliable values for these coefficients are essential for accurate fluid models, necessary for fusion and other applications (see for example Thomas et al. (Reference Thomas, Tzoufras, Robinson, Kingham, Ridgers, Sherlock and Bell2012) for a review). In the case of small Knudsen numbers, i.e. when the Coulomb mean free path is short compared to the relevant macroscopic gradients of the system, it is common to adopt a perturbative approach, where the equilibrium solution is a local Maxwellian distribution (Spitzer & Härm Reference Spitzer and Härm1953; Braginskii Reference Braginskii1958). In the small Knudsen limit, the distribution is (following our notation below) well approximated by the leading-order terms in a Cartesian expansion $f(\boldsymbol {p}) \approx {\mathsf{F}}^{(0)}+ {\mathsf{F}}^{({1})}_i p^{i}/p$![]() . The relevant transport coefficients can be determined by solving for $\boldsymbol{\mathsf{F}}^{({1})}(p)$
. The relevant transport coefficients can be determined by solving for $\boldsymbol{\mathsf{F}}^{({1})}(p)$![]() given $\boldsymbol{\mathsf{F}}^{(0)}(\boldsymbol {r}, p)$
given $\boldsymbol{\mathsf{F}}^{(0)}(\boldsymbol {r}, p)$![]() . In his seminal work, Braginskii (Reference Braginskii1958) derived approximate solutions using a truncated expansion in Laguerre (Sonine) polynomials. Other works applied a more direct numerical finite-difference approach (e.g. Epperlein & Haines Reference Epperlein and Haines1986). The transport coefficients that result from the two approaches differ in certain regimes, which Epperlein & Haines (Reference Epperlein and Haines1986) attributed to the finite truncation of the Laguerre polynomial expansion. However, convergence is still only accurate to the expansion order in the Knudsen number, which for larger values necessitates more terms in the particle anisotropy.
. In his seminal work, Braginskii (Reference Braginskii1958) derived approximate solutions using a truncated expansion in Laguerre (Sonine) polynomials. Other works applied a more direct numerical finite-difference approach (e.g. Epperlein & Haines Reference Epperlein and Haines1986). The transport coefficients that result from the two approaches differ in certain regimes, which Epperlein & Haines (Reference Epperlein and Haines1986) attributed to the finite truncation of the Laguerre polynomial expansion. However, convergence is still only accurate to the expansion order in the Knudsen number, which for larger values necessitates more terms in the particle anisotropy.
To improve the angular space resolution, one can expand $f$![]() as a series of Laplace's spherical harmonics (Allis Reference Allis1956; Bell et al. Reference Bell, Robinson, Sherlock, Kingham and Rozmus2006; Reville & Bell Reference Reville and Bell2013; Tzoufras et al. Reference Tzoufras, Tableman, Tsung, Mori and Bell2013)
as a series of Laplace's spherical harmonics (Allis Reference Allis1956; Bell et al. Reference Bell, Robinson, Sherlock, Kingham and Rozmus2006; Reville & Bell Reference Reville and Bell2013; Tzoufras et al. Reference Tzoufras, Tableman, Tsung, Mori and Bell2013)

Alternatively, one can expand $f$![]() in a series of Cartesian tensors (Johnston Reference Johnston1960; Shkarofsky, Johnston & Bachynski Reference Shkarofsky, Johnston and Bachynski1966; Epperlein & Haines Reference Epperlein and Haines1986; Thomas et al. Reference Thomas, Tzoufras, Robinson, Kingham, Ridgers, Sherlock and Bell2012)
in a series of Cartesian tensors (Johnston Reference Johnston1960; Shkarofsky, Johnston & Bachynski Reference Shkarofsky, Johnston and Bachynski1966; Epperlein & Haines Reference Epperlein and Haines1986; Thomas et al. Reference Thomas, Tzoufras, Robinson, Kingham, Ridgers, Sherlock and Bell2012)

where $p^{1}, p^{2}$![]() and $p^{3}$
and $p^{3}$![]() are the components of $\boldsymbol {p}$
are the components of $\boldsymbol {p}$![]() . The objects $\boldsymbol{\mathsf{F}}^{({l})}$
. The objects $\boldsymbol{\mathsf{F}}^{({l})}$![]() are called Cartesian tensors and its components ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
are called Cartesian tensors and its components ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() are the coefficients of the above expansion. Note that we are implicitly summing over all repeated indices. Moreover, the product of the components of $\boldsymbol {p}$
are the coefficients of the above expansion. Note that we are implicitly summing over all repeated indices. Moreover, the product of the components of $\boldsymbol {p}$![]() can be considered as a component of the (Cartesian) tensor $\otimes {\mathsf{p}}^{(l), i_{1} \ldots i_{l}} \equiv p^{i_{1}} \ldots p^{i_{l}}$
can be considered as a component of the (Cartesian) tensor $\otimes {\mathsf{p}}^{(l), i_{1} \ldots i_{l}} \equiv p^{i_{1}} \ldots p^{i_{l}}$![]() . Hence, the summation over repeated indices may be seen as a contraction of two tensors (formerly called a Cartesian tensor scalar product).
. Hence, the summation over repeated indices may be seen as a contraction of two tensors (formerly called a Cartesian tensor scalar product).
Both expansions can be substituted into (1.1) and the coefficients $f^{m}_{l}$![]() and ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
and ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() can be computed numerically or, depending on the complexity of the problem, analytically. Since both expansions of $f$
can be computed numerically or, depending on the complexity of the problem, analytically. Since both expansions of $f$![]() represent the same distribution function, there must exist a relation between $f^{m}_{l}$
represent the same distribution function, there must exist a relation between $f^{m}_{l}$![]() and ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
and ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() , see Courant & Hilbert (Reference Courant and Hilbert1953).
, see Courant & Hilbert (Reference Courant and Hilbert1953).
Johnston (Reference Johnston1960) investigated this relation and derived a way to express the components of the Cartesian tensors ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() as a sum containing the $f^{m}_{l}$
as a sum containing the $f^{m}_{l}$![]() for low values of $l$
for low values of $l$![]() , namely $l \leq ~4$
, namely $l \leq ~4$![]() . We revisit the problem of relating $f^{m}_{l}$
. We revisit the problem of relating $f^{m}_{l}$![]() and ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
and ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() and derive general formulae for converting between them (in both directions). We do not do this in the context of the distribution function $f$
and derive general formulae for converting between them (in both directions). We do not do this in the context of the distribution function $f$![]() and its expansions, but in the context of the multipole expansion of an electrostatic (or gravitational) potential. Also, the multipole expansion is either given as a Cartesian tensor or a spherical harmonic expansion. The expansion coefficients are called (Cartesian) multipole moments (i.e. monopole, dipole, quadrupole and high-order moments) or spherical multipole moments. The relation between these two kinds of moments is the same as the relation between ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
and its expansions, but in the context of the multipole expansion of an electrostatic (or gravitational) potential. Also, the multipole expansion is either given as a Cartesian tensor or a spherical harmonic expansion. The expansion coefficients are called (Cartesian) multipole moments (i.e. monopole, dipole, quadrupole and high-order moments) or spherical multipole moments. The relation between these two kinds of moments is the same as the relation between ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() and $f^{m}_{l}$
and $f^{m}_{l}$![]() , but multipole moments play an important role in multiple branches of physics, such as general relativity (Thorne Reference Thorne1980), molecular physics (Cipriani & Silvi Reference Cipriani and Silvi1982), plasma physics (Johnston Reference Johnston1960; Epperlein & Haines Reference Epperlein and Haines1986) and other areas like computational physics (Ludwig Reference Ludwig1991).
, but multipole moments play an important role in multiple branches of physics, such as general relativity (Thorne Reference Thorne1980), molecular physics (Cipriani & Silvi Reference Cipriani and Silvi1982), plasma physics (Johnston Reference Johnston1960; Epperlein & Haines Reference Epperlein and Haines1986) and other areas like computational physics (Ludwig Reference Ludwig1991).
Hence, in this paper, we derive a way to convert between the Cartesian multipole moments and the spherical multipole moments and apply it to convert between ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() and $f^{m}_{l}$
and $f^{m}_{l}$![]() . While the equivalence of the two multipole moments is long known (e.g. Courant & Hilbert Reference Courant and Hilbert1953, p. 517), systematic methods that relate them are not readily found in the literature.
. While the equivalence of the two multipole moments is long known (e.g. Courant & Hilbert Reference Courant and Hilbert1953, p. 517), systematic methods that relate them are not readily found in the literature.
In § 2.1, we begin with deriving a definition of the components of the Cartesian multipole moments. We will see that harmonic and homogeneous polynomials are part of this definition.
A polynomial $p$![]() of degree $l$
of degree $l$![]() is homogeneous if and only if
is homogeneous if and only if
Moreover, a polynomial $p$![]() is harmonic if it is a solution to Laplace's equation, i.e.
is harmonic if it is a solution to Laplace's equation, i.e.
We denote the space of homogeneous and harmonic polynomials of degree $l$![]() (in three variables) by $\mathcal {H}^{l}(\mathbb {R}^{3})$
(in three variables) by $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() .
.
We call the polynomials, which are part of the Cartesian multipole moment's definition, multipole functions and we show that a subset of these polynomials is a basis of $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() . We call this subset multipole basis functions.
. We call this subset multipole basis functions.
In § 2.2, we revisit the definition of the spherical multipole moments (prominently derived in Jackson Reference Jackson1998, p. 146). We will see that it contains (regular) solid harmonics. We prove that the solid harmonics are homogeneous and harmonic polynomials as well. Furthermore, we show that they are also a basis of $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() . We conclude that it is possible to find a basis transformation between the multipole basis functions and the solid harmonics. This basis transformation will allow us to express the spherical multipole moments in terms of the Cartesian multipole moments.
. We conclude that it is possible to find a basis transformation between the multipole basis functions and the solid harmonics. This basis transformation will allow us to express the spherical multipole moments in terms of the Cartesian multipole moments.
We can compute a preliminary basis transformation with the help of Efimov's definition of the Cartesian multipole moments (Efimov Reference Efimov1979), which we introduce in § 3. We prove that his definition and our definition are equivalent. In his definition, he uses a differential operator (Efimov's ladder operator) and, in conjunction with the ladder operator $L_{\pm }$![]() (known from the theory of angular momentum in Quantum Mechanics), Efimov derives the preliminary basis transformation, i.e. he derives a way to express the solid harmonics as a sum of the multipole functions.
(known from the theory of angular momentum in Quantum Mechanics), Efimov derives the preliminary basis transformation, i.e. he derives a way to express the solid harmonics as a sum of the multipole functions.
In § 4, we transform Efimov's expression for the solid harmonics, taking into account that only a subset of the multipole functions is a basis of $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() , to become an actual basis transformation between the solid harmonics and the multipole basis functions.
, to become an actual basis transformation between the solid harmonics and the multipole basis functions.
In § 5, we write the basis transformation as a matrix equation and compute the inverse basis transformation by inverting the basis transformation matrix. We show that inverting the basis transformation matrix is equivalent to invert four upper triangular matrices, if real solid harmonics are used and if they and the multipole basis functions are ordered in a specific way. The inverse basis transformation gives an expression of the multipole basis functions in terms of the solid harmonics. We use the basis transformation matrix and its inverse to present the relation between the Cartesian multipole moments and the spherical multipole moments in the form of a matrix equation.
In § 6, we come back to our original problem, namely the Vlasov–Fokker–Planck equation and the expansions of the distribution function $f$![]() . We apply the formalism, which we derived to convert between the Cartesian multipole moments and the spherical multipole moments, to solve it and reproduce the results found by Johnston (Reference Johnston1960).
. We apply the formalism, which we derived to convert between the Cartesian multipole moments and the spherical multipole moments, to solve it and reproduce the results found by Johnston (Reference Johnston1960).
We conclude the paper with a summary of the formalism to convert between the Cartesian multipole moments and the spherical multipole moments and assess it critically. Furthermore, we provide a link to the code of a command-line tool, which implements it.
2. Definition of the multipole moments
In electrodynamics (or equivalently, on exchanging constants, in gravitational theory), the multipole expansion is an expansion of the solution to Poisson's equation, namely
Either the denominator of the integrand is Taylor expanded in $r'/r$![]() or it is interpreted as the generating function of the Legendre polynomials. The former leads to the (Cartesian) multipole expansion with the Cartesian multipole moments and the latter to the spherical multipole expansion with the spherical multipole moments.
or it is interpreted as the generating function of the Legendre polynomials. The former leads to the (Cartesian) multipole expansion with the Cartesian multipole moments and the latter to the spherical multipole expansion with the spherical multipole moments.
In the first part of this section, we look at the Cartesian multipole expansion and derive a definition of the Cartesian multipole moments. The second part dedicates itself to the spherical multipole expansion and investigates the definition of the spherical multipole moments.
2.1. Definition of the Cartesian multipole moments
In textbooks (e.g. Jackson Reference Jackson1998, p. 146), no general definition of the Cartesian multipole moments is given. Instead, the Taylor expansion of the denominator in the integrand of (2.1) is computed up to, for example, second order, i.e.

The potential then becomes
The primed and unprimed components may be interchanged. As an example, consider the second-order term:
where we used that $r^{2}\delta ^{ij}x'_{i}x'_{j} = r'^{2}\delta _{ij} x^{i} x^{j}$![]() . This transforms the potential into
. This transforms the potential into
with the usual definitions of the monopole and the dipole. The components of the quadrupole moment are defined as
Hence, a general method to define the components of the Cartesian multipole moment of an arbitrary order $l$![]() consists in taking $l$
consists in taking $l$![]() partial derivatives of $1/r$
partial derivatives of $1/r$![]() and interchanging the components of $\boldsymbol {r}$
and interchanging the components of $\boldsymbol {r}$![]() and $\boldsymbol {r}'$
and $\boldsymbol {r}'$![]() , as in the above example. However, note that the interchange did not change the (functional) form of the numerator of $\partial _{i}\partial _{j}1/r$
, as in the above example. However, note that the interchange did not change the (functional) form of the numerator of $\partial _{i}\partial _{j}1/r$![]() , it merely replaced the components of $\boldsymbol {r}$
, it merely replaced the components of $\boldsymbol {r}$![]() with the components of $\boldsymbol {r}'$
with the components of $\boldsymbol {r}'$![]() . This implies that we could alternatively have obtained the expression in parentheses in the quadrupole moment's definition by computing $\partial '_{i}\partial '_{j} 1/r'$
. This implies that we could alternatively have obtained the expression in parentheses in the quadrupole moment's definition by computing $\partial '_{i}\partial '_{j} 1/r'$![]() and ‘removing’ the denominator. This is the idea behind our definition of the components of the Cartesian multipole moment of rank $l$
and ‘removing’ the denominator. This is the idea behind our definition of the components of the Cartesian multipole moment of rank $l$![]() , which is
, which is
Here, the calligraphic $\mathcal {K}$![]() denotes the Kelvin transform (Axler, Bourdon & Wade Reference Axler, Bourdon and Wade2001, p. 61), which is defined as
denotes the Kelvin transform (Axler, Bourdon & Wade Reference Axler, Bourdon and Wade2001, p. 61), which is defined as
Applying the definition to the $l = 2$![]() case recovers the quadrupole moment and demonstrates in which sense the Kelvin transform removes the denominator. With this definition at hand, the (Cartesian) multipole expansion is
case recovers the quadrupole moment and demonstrates in which sense the Kelvin transform removes the denominator. With this definition at hand, the (Cartesian) multipole expansion is

Of course, the first three multipole moments are the monopole ${\mathsf{Q}}^{({0})} = q$![]() , the dipole moment ${\mathsf{Q}}^{({1})}_{i} = d_{i}$
, the dipole moment ${\mathsf{Q}}^{({1})}_{i} = d_{i}$![]() and the quadrupole moment ${\mathsf{Q}}^{({2})}_{ij} = {\mathsf{Q}}_{ij}$
and the quadrupole moment ${\mathsf{Q}}^{({2})}_{ij} = {\mathsf{Q}}_{ij}$![]() .
.
We show now that the definition in (2.7) gives the known Cartesian multipole moments for an arbitrary rank $l$![]() . The definition is correct if for all $l$
. The definition is correct if for all $l$![]() , the interchange of $\boldsymbol {r}$
, the interchange of $\boldsymbol {r}$![]() and $\boldsymbol {r}'$
and $\boldsymbol {r}'$![]() does not change the form of the numerator of the $l$
does not change the form of the numerator of the $l$![]() th partial derivative of $1/r$
th partial derivative of $1/r$![]() and if the Kelvin transform removes its denominator.
and if the Kelvin transform removes its denominator.
A sufficient condition for the Kelvin transform to remove the denominator is that the numerator of the $l$![]() th partial derivative of $1/r$
th partial derivative of $1/r$![]() is an homogeneous polynomial (see (1.4)). That this is a sufficient condition can be seen by noting that
is an homogeneous polynomial (see (1.4)). That this is a sufficient condition can be seen by noting that
where ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is an as yet undetermined function (the above equality can be proven by induction). The indices reflect that the function is different for different values of the indices. We call these functions multipole functions. Moreover, Axler, while proving Lemma 5.15 in Axler et al. (Reference Axler, Bourdon and Wade2001, p. 86), shows that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$
is an as yet undetermined function (the above equality can be proven by induction). The indices reflect that the function is different for different values of the indices. We call these functions multipole functions. Moreover, Axler, while proving Lemma 5.15 in Axler et al. (Reference Axler, Bourdon and Wade2001, p. 86), shows that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is an homogeneous polynomial of degree $l$
is an homogeneous polynomial of degree $l$![]() . Taking the Kelvin transform then yields
. Taking the Kelvin transform then yields

which shows that it suffices that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is an homogeneous polynomial to remove the denominator.
is an homogeneous polynomial to remove the denominator.
In the example of the second-order term, the interchange of $\boldsymbol {r}$![]() and $\boldsymbol {r}'$
and $\boldsymbol {r}'$![]() did not change the (functional) form of ${\mathsf{M}}^{({2})}_{ij}$
did not change the (functional) form of ${\mathsf{M}}^{({2})}_{ij}$![]() because this form was ‘somehow’ special. We already know that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$
because this form was ‘somehow’ special. We already know that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is an homogeneous polynomial of degree $l$
is an homogeneous polynomial of degree $l$![]() . We can further restrict its form. Remember that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$
. We can further restrict its form. Remember that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is the numerator of $g(\boldsymbol {r}) \equiv \partial _{i_{1}} \ldots \partial _{i_{l}} 1/r$
is the numerator of $g(\boldsymbol {r}) \equiv \partial _{i_{1}} \ldots \partial _{i_{l}} 1/r$![]() . The following two considerations fix its form.
. The following two considerations fix its form.
First, the form of the function $g$![]() does not change if it is defined in a rotated coordinate system. Assume that the relation between the rotated coordinates $\hat {\boldsymbol {r}}$
does not change if it is defined in a rotated coordinate system. Assume that the relation between the rotated coordinates $\hat {\boldsymbol {r}}$![]() and the original coordinates $\boldsymbol {r}$
and the original coordinates $\boldsymbol {r}$![]() is $\hat {\boldsymbol {r}} = \boldsymbol{\mathsf{A}}\boldsymbol {r}$
is $\hat {\boldsymbol {r}} = \boldsymbol{\mathsf{A}}\boldsymbol {r}$![]() . The former statement then says that $\hat {g}(\hat {\boldsymbol {r}}) = g(\hat {\boldsymbol {r}})$
. The former statement then says that $\hat {g}(\hat {\boldsymbol {r}}) = g(\hat {\boldsymbol {r}})$![]() , where $\hat {g}(\hat {\boldsymbol {r}}) \equiv \hat {\partial }_{i_{1}} \ldots \hat {\partial }_{i_{l}} 1/\hat {r}$
, where $\hat {g}(\hat {\boldsymbol {r}}) \equiv \hat {\partial }_{i_{1}} \ldots \hat {\partial }_{i_{l}} 1/\hat {r}$![]() . A comparison of $g$
. A comparison of $g$![]() 's definition and $\hat {g}$
's definition and $\hat {g}$![]() proves it. This restricts the form of the numerator of $g$
proves it. This restricts the form of the numerator of $g$![]() , as the following example for $l = 2$
, as the following example for $l = 2$![]() illustrates:
illustrates:
where we used that $\hat {r} = r$![]() and $\hat {\boldsymbol {\nabla }} = \boldsymbol{\mathsf{A}} \boldsymbol {\nabla }$
and $\hat {\boldsymbol {\nabla }} = \boldsymbol{\mathsf{A}} \boldsymbol {\nabla }$![]() . Note the rotation matrices must either transform a component of $\boldsymbol {r}$
. Note the rotation matrices must either transform a component of $\boldsymbol {r}$![]() or they must be multiplied with each other, i.e. $({\mathsf{A}})_{i}^{k}({\mathsf{A}})_{j}^{l} \delta _{kl}= ({\mathsf{A}})_{i}^{k}({\mathsf{A}}^{T})_{kj} = \delta _{ij}$
or they must be multiplied with each other, i.e. $({\mathsf{A}})_{i}^{k}({\mathsf{A}})_{j}^{l} \delta _{kl}= ({\mathsf{A}})_{i}^{k}({\mathsf{A}}^{T})_{kj} = \delta _{ij}$![]() . Hence, all the terms of ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$
. Hence, all the terms of ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() must be products of components of $\boldsymbol {r}$
must be products of components of $\boldsymbol {r}$![]() and Kronecker deltas to ‘cope’ with the $l$
and Kronecker deltas to ‘cope’ with the $l$![]() rotation matrices which appear as a consequence of $\hat {g}(\hat {\boldsymbol {r}}) = g(\hat {\boldsymbol {r}})$
rotation matrices which appear as a consequence of $\hat {g}(\hat {\boldsymbol {r}}) = g(\hat {\boldsymbol {r}})$![]() .
.
Second, the exchange of any two of the indices in $g$![]() 's definition does not change its numerator, because it is possible to exchange the partial derivatives with each other (Schwarz's theorem). Hence, the object ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$
's definition does not change its numerator, because it is possible to exchange the partial derivatives with each other (Schwarz's theorem). Hence, the object ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is symmetric in all its indices. This implies that a sum of the mentioned products of components of $\boldsymbol {r}$
is symmetric in all its indices. This implies that a sum of the mentioned products of components of $\boldsymbol {r}$![]() and Kronecker deltas is needed. For example, consider the $l = 3$
and Kronecker deltas is needed. For example, consider the $l = 3$![]() case,
case,
where $c_{3,0}, c_{3,1} \in \mathbb {R}$![]() are coefficients. Note that the sum is over pairs of indices and that this guarantees that any two of the indices can be exchanged without changing ${\mathsf{M}}^{({3})}_{ijk}$
are coefficients. Note that the sum is over pairs of indices and that this guarantees that any two of the indices can be exchanged without changing ${\mathsf{M}}^{({3})}_{ijk}$![]() . The factor $r^{2}$
. The factor $r^{2}$![]() reflects that ${\mathsf{M}}^{({3})}_{ijk}$
reflects that ${\mathsf{M}}^{({3})}_{ijk}$![]() must be an homogeneous polynomial of degree three.
must be an homogeneous polynomial of degree three.
In summary, the fact that ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is an homogeneous polynomial of degree $l$
is an homogeneous polynomial of degree $l$![]() that can be invariantly defined in a rotated coordinate system and that is symmetric in its indices implies that its functional form must be
that can be invariantly defined in a rotated coordinate system and that is symmetric in its indices implies that its functional form must be

where $\lfloor x \rfloor$![]() is the floor function. We also introduce $R_{l,2k} \equiv {P}(\delta _{i_{1}i_{2}} \ldots \delta _{i_{2k-1}i_{2k}} x_{i_{2k + 1}} \ldots x_{i_{l}})$
is the floor function. We also introduce $R_{l,2k} \equiv {P}(\delta _{i_{1}i_{2}} \ldots \delta _{i_{2k-1}i_{2k}} x_{i_{2k + 1}} \ldots x_{i_{l}})$![]() , where ${P}$
, where ${P}$![]() is an operator which produces the sum over the pairs of indices needed to assure symmetry (cf. with the previous example). This operator hides a lot of the complexity, but is explained in detail in Appendix A.2. A closed-form expression for the coefficients $c_{l,k}$
is an operator which produces the sum over the pairs of indices needed to assure symmetry (cf. with the previous example). This operator hides a lot of the complexity, but is explained in detail in Appendix A.2. A closed-form expression for the coefficients $c_{l,k}$![]() is derived in Appendix A.3. Similar arguments are used by Efimov to fix the functional form of the multipole functions (Efimov Reference Efimov1979, p. 426).
is derived in Appendix A.3. Similar arguments are used by Efimov to fix the functional form of the multipole functions (Efimov Reference Efimov1979, p. 426).
This is the ‘somehow’ special (functional) form of the multipole functions ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() which permits that the interchange of $\boldsymbol {r}$
which permits that the interchange of $\boldsymbol {r}$![]() and $\boldsymbol {r}'$
and $\boldsymbol {r}'$![]() does not change the form but only replaces the components of $\boldsymbol {r}$
does not change the form but only replaces the components of $\boldsymbol {r}$![]() with the components of $\boldsymbol {r}'$
with the components of $\boldsymbol {r}'$![]() . To see this, note that, in the light of (2.10) and (2.14), a term in the Taylor expansion of (2.2) of arbitrary order $l$
. To see this, note that, in the light of (2.10) and (2.14), a term in the Taylor expansion of (2.2) of arbitrary order $l$![]() contains
contains
Using that the exponent of $r^{2k}$![]() is even and remembering that $r^{2}\delta ^{ij}x'_{i}x'_{j} = r'^{2}\delta _{ij}x^{i}x^{j}$
is even and remembering that $r^{2}\delta ^{ij}x'_{i}x'_{j} = r'^{2}\delta _{ij}x^{i}x^{j}$![]() , we can replace the components of $\boldsymbol {r}$
, we can replace the components of $\boldsymbol {r}$![]() and $\boldsymbol {r}'$
and $\boldsymbol {r}'$![]() .
.
We conclude that the definition of the Cartesian multipole moments introduced in (2.7) is correct. The $\boldsymbol{\mathsf{Q}}^{({l})}$![]() are tensors, i.e. they transform as required under coordinate transformations. In Appendix A.1, we use our definition to prove this.
are tensors, i.e. they transform as required under coordinate transformations. In Appendix A.1, we use our definition to prove this.
Before we close this section, we emphasise that the multipole functions ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() are harmonic functions, i.e.
are harmonic functions, i.e.
This is also proven in (the already quoted) Lemma 5.15 in Axler et al. (Reference Axler, Bourdon and Wade2001, p. 86).
In what follows, it is convenient to introduce a different notation for the indices of $\boldsymbol{\mathsf{M}}^{({l})}$![]() , namely
, namely
This notation implicitly takes advantage of the symmetry. For example, ${\mathsf{M}}^{({3})}_{112} = {\mathsf{M}}^{({3})}_{121}$![]() in the ${\mathsf{M}}^{({l})}_{i_1\dots i_l}$
in the ${\mathsf{M}}^{({l})}_{i_1\dots i_l}$![]() notation and both components are ${\mathsf{M}}^{({3})}_{210}$
notation and both components are ${\mathsf{M}}^{({3})}_{210}$![]() in the newly introduced $pqr$
in the newly introduced $pqr$![]() notation.
notation.
Last, but not least, Axler shows in Theorem 5.25 in Axler et al. (Reference Axler, Bourdon and Wade2001, p. 92) that
In words, the functions ${\mathsf{M}}^{({l})}_{pqr}$![]() are homogeneous and harmonic polynomials of degree $l$
are homogeneous and harmonic polynomials of degree $l$![]() , and a subset of them is a basis of the space of these polynomials. We call this subset the multipole basis functions.
, and a subset of them is a basis of the space of these polynomials. We call this subset the multipole basis functions.
2.2. Definition of the spherical multipole moments
The denominator of the integrand in (2.1) can be interpreted as the generating function of the Legendre polynomials, i.e.

Here, $\gamma$![]() is the angle between $\boldsymbol {r}$
is the angle between $\boldsymbol {r}$![]() and $\boldsymbol {r}'$
and $\boldsymbol {r}'$![]() (Jackson Reference Jackson1998, p. 102, (3.38)). Together with the addition theorem for Laplace's spherical harmonics (cf. Jackson Reference Jackson1998, p. 110, (3.62)), which is
(Jackson Reference Jackson1998, p. 102, (3.38)). Together with the addition theorem for Laplace's spherical harmonics (cf. Jackson Reference Jackson1998, p. 110, (3.62)), which is

we obtain the spherical multipole expansion

The function $r^{l}Y^{m}_{l}(\theta, \varphi )$![]() is called a solid harmonic of degree $l$
is called a solid harmonic of degree $l$![]() and order $m$
and order $m$![]() . Furthermore, we call the coefficients $q^{m}_{l}$
. Furthermore, we call the coefficients $q^{m}_{l}$![]() spherical multipole moments (Jackson Reference Jackson1998, p. 145). They are defined as
spherical multipole moments (Jackson Reference Jackson1998, p. 145). They are defined as
A (Laplace's) spherical harmonic of degree $l$![]() and order $m$
and order $m$![]() is (cf. Jackson Reference Jackson1998, p. 108, (3.53))
is (cf. Jackson Reference Jackson1998, p. 108, (3.53))

Here, $N^{m}_{l}$![]() is the normalisation and the functions $P^{m}_{l}$
is the normalisation and the functions $P^{m}_{l}$![]() are the associated Legendre polynomials.
are the associated Legendre polynomials.
The solid harmonics are homogeneous polynomials of degree $l$![]() . This can be seen by using the following definition of the associated Legendre polynomials (cf. Jackson Reference Jackson1998, p. 108, (3.49)):
. This can be seen by using the following definition of the associated Legendre polynomials (cf. Jackson Reference Jackson1998, p. 108, (3.49)):
Then, the solid harmonics with order greater than or equal to zero ($m \geq 0$![]() ) are
) are

The $a_{k} \in \mathbb {R}$![]() are coefficients, which collect numerical factors. In the second equation, we expressed the spherical coordinates in Cartesian coordinates and exploited that the $m$
are coefficients, which collect numerical factors. In the second equation, we expressed the spherical coordinates in Cartesian coordinates and exploited that the $m$![]() th derivative of a degree $l$
th derivative of a degree $l$![]() polynomial yields a degree $l-m$
polynomial yields a degree $l-m$![]() polynomial. The Legendre polynomials, in particular, consist of either odd or even powers of $\cos \theta$
polynomial. The Legendre polynomials, in particular, consist of either odd or even powers of $\cos \theta$![]() . It can be checked that the definition of an homogeneous polynomial of degree $l$
. It can be checked that the definition of an homogeneous polynomial of degree $l$![]() , which was given in (1.4), applies to $p$
, which was given in (1.4), applies to $p$![]() as defined in (2.25). The argument holds true for negative $m$
as defined in (2.25). The argument holds true for negative $m$![]() as well. In this case, $(x + \mathrm {i} y)^{m}$
as well. In this case, $(x + \mathrm {i} y)^{m}$![]() becomes $(x - \mathrm {i} y)^{m}$
becomes $(x - \mathrm {i} y)^{m}$![]() . The definition of an homogeneous polynomial still applies.
. The definition of an homogeneous polynomial still applies.
Furthermore, the solid harmonics (as their name suggests) are harmonic functions. In spherical coordinates the Laplace operator can be split into a radial part and an angular part, i.e. $\varDelta = \varDelta _{r} + \varDelta _{\theta, \varphi }/r^{2}$![]() . Laplace's spherical harmonics are eigenfunctions of the angular part with eigenvalue $-l(l+1)$
. Laplace's spherical harmonics are eigenfunctions of the angular part with eigenvalue $-l(l+1)$![]() (Landau & Lifshitz Reference Landau and Lifshitz1977, p. 91, (28.7)). Hence,
(Landau & Lifshitz Reference Landau and Lifshitz1977, p. 91, (28.7)). Hence,
We conclude this section by proving
i.e. the solid harmonics are also a basis of the space of homogeneous and harmonic polynomials.
We proceed in two steps. First, we determine the dimension of $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() and, second, we show that the solid harmonics are independent. The dimension of $\mathcal {H}^{l}(\mathbb {R}^{3})$
and, second, we show that the solid harmonics are independent. The dimension of $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() is $2~l + 1$
is $2~l + 1$![]() . This can be derived in different ways, for example, as in Müller (Reference Müller1966, p. 11, (11)) or, alternatively, as done by Axler in Proposition 5.8 in Axler et al. (Reference Axler, Bourdon and Wade2001, p. 78). Note that there are $2l + 1$
. This can be derived in different ways, for example, as in Müller (Reference Müller1966, p. 11, (11)) or, alternatively, as done by Axler in Proposition 5.8 in Axler et al. (Reference Axler, Bourdon and Wade2001, p. 78). Note that there are $2l + 1$![]() solid harmonics of degree $l$
solid harmonics of degree $l$![]() . The linear independence follows from the orthogonality of Laplace's spherical harmonics, namely (cf. Jackson Reference Jackson1998, p. 108, (3.55))
. The linear independence follows from the orthogonality of Laplace's spherical harmonics, namely (cf. Jackson Reference Jackson1998, p. 108, (3.55))
Hence, (2.27) is proven.
We gave explicit definitions of the Cartesian multipole moments and the spherical multipole moments. Both definitions contained homogeneous and harmonic polynomials: the multipole functions ${\mathsf{M}}^{({l})}_{pqr}$![]() in the former case, solid harmonics $r^{l}Y^{m}_{l}$
in the former case, solid harmonics $r^{l}Y^{m}_{l}$![]() in the latter. Moreover, a subset of the functions ${\mathsf{M}}^{({l})}_{pqr}$
in the latter. Moreover, a subset of the functions ${\mathsf{M}}^{({l})}_{pqr}$![]() (namely, the multipole basis functions) are a basis of $\mathcal {H}^{l}(\mathbb {R}^{3})$
(namely, the multipole basis functions) are a basis of $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() . The same is true of the solid harmonics. Hence, the relation between the Cartesian multipole moments and spherical multipole moments can be formalised as a basis transformation between the solid harmonics and the multipole basis functions. In the next section, we introduce Efimov's ladder operator to derive the basis transformation.
. The same is true of the solid harmonics. Hence, the relation between the Cartesian multipole moments and spherical multipole moments can be formalised as a basis transformation between the solid harmonics and the multipole basis functions. In the next section, we introduce Efimov's ladder operator to derive the basis transformation.
3. Efimov's ladder operator
3.1. An alternative definition of the Cartesian multipole moments
In their paper on multipole moments, Efimov derives an alternative definition of the Cartesian multipole moments (Efimov Reference Efimov1979). To derive it, they multiply the Taylor expansion given in (2.2) by $r$![]() , which yields
, which yields

Taking advantage of the fact that the functions ${\mathsf{M}}^{({l})}_{i_{1} \ldots {i_{l}}}$![]() are homogeneous polynomials of degree $l$
are homogeneous polynomials of degree $l$![]() and using the definition of $\tilde {\boldsymbol {r}}$
and using the definition of $\tilde {\boldsymbol {r}}$![]() (see (2.8)) leads to the equivalent equation
(see (2.8)) leads to the equivalent equation

Since every term of the sums on both sides of the equation is an homogeneous polynomial of the same degree, one finds
Note the derivatives on the left-hand side of the equation are taken with respect to $\boldsymbol {r}$![]() (and not $\tilde {\boldsymbol {r}}$
(and not $\tilde {\boldsymbol {r}}$![]() ). We may rewrite the above to get a convenient grouping:
). We may rewrite the above to get a convenient grouping:

The expression in parentheses is Efimov's ladder operator. We introduce the notation
which on applying $l$![]() times turns (3.3) into
times turns (3.3) into
Here, $\mathbf {1}(\boldsymbol {r}) = 1$![]() is a constant function. This implies an alternative definition of the multipole functions
is a constant function. This implies an alternative definition of the multipole functions
Replacing the Kelvin transform in (2.7) with Efimov's ladder operator yields an alternative definition for the Cartesian multipole moments as well.
We explicitly prove that the two definitions of the multipole functions are equivalent, i.e.
The first step consists in showing that

This can be proven by induction. A quick computation shows that the statement holds true for the base case $l = 1$![]() . From (2.10), and noting that $\mathcal {K}[\mathcal {K}[f]] = f$
. From (2.10), and noting that $\mathcal {K}[\mathcal {K}[f]] = f$![]() , it follows that
, it follows that
Taking the derivative with respect to $x_{j}$![]() yields
yields
Note that acting with the expression in parentheses on ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() gives an homogeneous polynomial of degree $l + 1$
gives an homogeneous polynomial of degree $l + 1$![]() . We again take the Kelvin transform, use the induction hypothesis and see that
. We again take the Kelvin transform, use the induction hypothesis and see that

Relabelling the indices ($j \rightarrow i_{1}$![]() and $i_{k} \rightarrow i_{k + 1}$
and $i_{k} \rightarrow i_{k + 1}$![]() ) and shifting the index of the product by one, yields the conclusion.
) and shifting the index of the product by one, yields the conclusion.
In a second step, we prove that each factor in the product in (3.9) is equivalent to Efimov's ladder operator. We choose an arbitrary factor with index $k$![]() equal to $n$
equal to $n$![]() and express the right-hand side of (3.9) as
and express the right-hand side of (3.9) as
where we used that

To show that the factor in (3.13) corresponding to the index $k = n$![]() and ${{D}}_{i_{n}}$
and ${{D}}_{i_{n}}$![]() are equivalent, we have to prove that
are equivalent, we have to prove that
This equality holds because the function $u \equiv {\mathsf{M}}^{({l-n})}_{i_{n+1} \ldots i_{l}}$![]() is an homogeneous polynomial of degree $l-n$
is an homogeneous polynomial of degree $l-n$![]() . Note that every homogeneous polynomial of an arbitrary degree $l$
. Note that every homogeneous polynomial of an arbitrary degree $l$![]() can be written as a linear combination of monomials $x^{j_{1}} \ldots x^{j_{l}}$
can be written as a linear combination of monomials $x^{j_{1}} \ldots x^{j_{l}}$![]() , i.e. $p(\boldsymbol {r}) = \alpha _{j_{1} \ldots j_{l}}x^{j_{1}} \ldots x^{j_{l}}$
, i.e. $p(\boldsymbol {r}) = \alpha _{j_{1} \ldots j_{l}}x^{j_{1}} \ldots x^{j_{l}}$![]() . Here, $\alpha$
. Here, $\alpha$![]() is a collection of coefficients. There are $(l + 2)(l + 1)/2$
is a collection of coefficients. There are $(l + 2)(l + 1)/2$![]() different monomials. If the object ${\boldsymbol{\mathsf{\alpha}}}$
different monomials. If the object ${\boldsymbol{\mathsf{\alpha}}}$![]() is symmetric in all its indices, it contains an equal amount of independent coefficients. Thus, there exists a symmetric ${\boldsymbol{\mathsf{\alpha}}}$
is symmetric in all its indices, it contains an equal amount of independent coefficients. Thus, there exists a symmetric ${\boldsymbol{\mathsf{\alpha}}}$![]() such that $u(\boldsymbol {r}) = \alpha _{j_{1} \ldots j_{l-n}} x^{j_{1}} \ldots x^{j_{l-n}}$
such that $u(\boldsymbol {r}) = \alpha _{j_{1} \ldots j_{l-n}} x^{j_{1}} \ldots x^{j_{l-n}}$![]() . This implies that
. This implies that

In the second line, we used that ${\boldsymbol{\mathsf{\alpha}}}$![]() is symmetric. Since $n$
is symmetric. Since $n$![]() was arbitrary, we conclude that all factors in the product in (3.9) are equivalent to a corresponding component of the ladder operator $\boldsymbol {{{D}}}$
was arbitrary, we conclude that all factors in the product in (3.9) are equivalent to a corresponding component of the ladder operator $\boldsymbol {{{D}}}$![]() .
.
Before we end this section, we use the alternative definition of the Cartesian multipole moments (and the multipole functions) to learn more about them.
We first note that Efimov's ladder operators commute, i.e.
Note that this must be the case, because ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() must be symmetric. Moreover,
must be symmetric. Moreover,
An immediate consequence of these two equations is that
We say that the object ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is traceless, i.e. the contraction of two arbitrary indices is zero (cf. Efimov Reference Efimov1979, (1.5)–(1.7)). This property is carried over to the Cartesian multipole moments. Thus, the Cartesian multipole moments $\boldsymbol{\mathsf{Q}}^{({l})}$
is traceless, i.e. the contraction of two arbitrary indices is zero (cf. Efimov Reference Efimov1979, (1.5)–(1.7)). This property is carried over to the Cartesian multipole moments. Thus, the Cartesian multipole moments $\boldsymbol{\mathsf{Q}}^{({l})}$![]() are symmetric and traceless tensors of rank $l$
are symmetric and traceless tensors of rank $l$![]() .
.
We pointed out that an homogeneous polynomial of degree $l$![]() can be written as a linear combination of monomials with the help of a symmetric collection of coefficients ${\boldsymbol{\mathsf{\alpha}}}$
can be written as a linear combination of monomials with the help of a symmetric collection of coefficients ${\boldsymbol{\mathsf{\alpha}}}$![]() . It can be shown that if the polynomial is harmonic as well, ${\boldsymbol{\mathsf{\alpha}}}$
. It can be shown that if the polynomial is harmonic as well, ${\boldsymbol{\mathsf{\alpha}}}$![]() must be traceless (Jeevanjee Reference Jeevanjee2011, ex. 3.26). This implies that not only the multipole functions ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$
must be traceless (Jeevanjee Reference Jeevanjee2011, ex. 3.26). This implies that not only the multipole functions ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() are homogeneous and harmonic polynomials, but also the functions in the Cartesian multipole expansion in (2.9), namely
are homogeneous and harmonic polynomials, but also the functions in the Cartesian multipole expansion in (2.9), namely
are homogeneous and harmonic polynomials of degree $l$![]() .
.
3.2. Preliminary basis transformation
With the tools derived up to now, we are in a position to express the solid harmonics as a sum of the multipole functions ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() .
.
We start again with the denominator of the integrand in (2.1). We fix $\boldsymbol {r}'$![]() to be the unit vector pointing into the $z$
to be the unit vector pointing into the $z$![]() -direction. This implies
-direction. This implies

We used the Taylor expansion given in (2.2) for the left-hand side and (2.19) for the right-hand side of the last equation. Since $\boldsymbol {r}' = \boldsymbol {e}_{z}$![]() , the angle $\gamma$
, the angle $\gamma$![]() is the polar angle $\theta$
is the polar angle $\theta$![]() . We take the Kelvin transform of this equation, i.e.
. We take the Kelvin transform of this equation, i.e.

Note that the Kelvin transform's definition implies that it is linear, namely $\mathcal {K}[f + \lambda g] = \mathcal {K}[f] + \lambda \mathcal {K}[g]$![]() . We now use that $N^{0}_{l} r^{l} P_{l} = r^{l}Y^{0}_{l}$
. We now use that $N^{0}_{l} r^{l} P_{l} = r^{l}Y^{0}_{l}$![]() . Furthermore, since a solid harmonic of degree $l$
. Furthermore, since a solid harmonic of degree $l$![]() is an homogeneous polynomial of degree $l$
is an homogeneous polynomial of degree $l$![]() , the Kelvin transform removes the denominator of the right-hand side of the last equation (cf. § 2.1). Together with the equivalence of the Kelvin transform of the partial derivatives of $1/r$
, the Kelvin transform removes the denominator of the right-hand side of the last equation (cf. § 2.1). Together with the equivalence of the Kelvin transform of the partial derivatives of $1/r$![]() and Efimov's ladder operator, we obtain the equivalent statement
and Efimov's ladder operator, we obtain the equivalent statement

Since every term on both sides of the equation is a polynomial of the same degree (namely $l$![]() ), the equation implies that
), the equation implies that
Compare with Efimov (Reference Efimov1979, p. 428, (2.9)) and note that the notation introduced in (2.17) is used for the indices of the multipole function.
To express a solid harmonic of order $m$![]() greater than zero as a sum of multipole functions, we use that Laplace's spherical harmonics $Y^{m}_{l}$
greater than zero as a sum of multipole functions, we use that Laplace's spherical harmonics $Y^{m}_{l}$![]() appear as the common eigenfunctions of the square of the angular momentum operator (known from Quantum Mechanics) and one of its components. The angular momentum operator is defined as (cf. Landau & Lifshitz Reference Landau and Lifshitz1977, p. 83, (26.2))
appear as the common eigenfunctions of the square of the angular momentum operator (known from Quantum Mechanics) and one of its components. The angular momentum operator is defined as (cf. Landau & Lifshitz Reference Landau and Lifshitz1977, p. 83, (26.2))
We are particularly interested in the angular momentum ladder operator
The last line shows the ladder operator in spherical coordinates (Landau & Lifshitz Reference Landau and Lifshitz1977, p. 85, (26.15)). The ladder operators are used to increase (or decrease) the order of a spherical harmonic, e.g.
The numerical factor is an implication of (27.12) in Landau & Lifshitz (Reference Landau and Lifshitz1977, p. 89). We can apply this operator $m$![]() times to (3.24) and we get
times to (3.24) and we get

where we used the fact that $\mathrm {L}_{+}$![]() does not contain a derivative with respect to $r$
does not contain a derivative with respect to $r$![]() , as can be seen in (3.26). We can compute the commutator of $\mathrm {L}_{+}$
, as can be seen in (3.26). We can compute the commutator of $\mathrm {L}_{+}$![]() and ${{D}}_{z}$
and ${{D}}_{z}$![]() . This yields
. This yields
This computation is done in detail in Appendix B.
One can prove by induction that
which, when substituted into the previously derived expression for $r^{l}Y^{m}_{l}$![]() , yields the final result of this section: the preliminary basis transformation, i.e.
, yields the final result of this section: the preliminary basis transformation, i.e.

Here, $m \geq 0$![]() and we used the notation of (2.17) for the indices of the multipole functions. The factor is
and we used the notation of (2.17) for the indices of the multipole functions. The factor is

We called this expression for the solid harmonics a preliminary basis transformation, because the sum on the right-hand side of (3.31) contains multipole functions with $p > 1$![]() , which are not multipole basis functions. The solid harmonics with negative order $m$
, which are not multipole basis functions. The solid harmonics with negative order $m$![]() are obtained with the help of $Y^{-m}_{l} = (-1)^{m}{Y^{m}_{l}}^{*}$
are obtained with the help of $Y^{-m}_{l} = (-1)^{m}{Y^{m}_{l}}^{*}$![]() (Jackson Reference Jackson1998, p. 146, (4.3), (4.7)). Efimov derived (3.31) with similar arguments (see Efimov Reference Efimov1979, p. 429, (2.10)).
(Jackson Reference Jackson1998, p. 146, (4.3), (4.7)). Efimov derived (3.31) with similar arguments (see Efimov Reference Efimov1979, p. 429, (2.10)).
The preliminary basis transformation already allows to express spherical multipole moments in terms of Cartesian multipole moments. We can take the complex conjugate of (3.31) and plug it into the definition of the spherical multipole moments (see (2.22)) and obtain

In his textbook ‘Classical Electrodynamics’, Jackson computes the spherical multipole moments with degree $l = 0, 1$![]() and $2$
and $2$![]() (Jackson Reference Jackson1998, p. 146). The above formula allows a computation for arbitrary $l$
(Jackson Reference Jackson1998, p. 146). The above formula allows a computation for arbitrary $l$![]() and $m$
and $m$![]() . For example,
. For example,

In the last equation, we used the conventional tensor indices, namely ${\mathsf{Q}}^{({3})}_{ijk}$![]() .
.
4. Basis transformation
As already pointed out, we called the expression derived in (3.31) a preliminary basis transformation, because the sum on the right-hand side contained multipole functions with index $p > 1$![]() . However, only the multipole functions with $p \leq ~1$
. However, only the multipole functions with $p \leq ~1$![]() are a basis of the space of homogeneous and harmonic polynomials of degree $l$
are a basis of the space of homogeneous and harmonic polynomials of degree $l$![]() (see (2.18)). To turn (3.31) into an actual basis transformation, we have to express all ${\mathsf{M}}^{({l})}_{pqr}$
(see (2.18)). To turn (3.31) into an actual basis transformation, we have to express all ${\mathsf{M}}^{({l})}_{pqr}$![]() with $p > 1$
with $p > 1$![]() as a linear combination of the multipole basis functions.
as a linear combination of the multipole basis functions.
We can accomplish this by exploiting that the object $\boldsymbol{\mathsf{M}}^{({l})}$![]() is symmetric and traceless (cf. (3.19)). In a first step, we use the notation for the indices of $\boldsymbol{\mathsf{M}}^{({l})}$
is symmetric and traceless (cf. (3.19)). In a first step, we use the notation for the indices of $\boldsymbol{\mathsf{M}}^{({l})}$![]() , which we introduced in (2.17), to express the latter property of $\boldsymbol{\mathsf{M}}^{({l})}$
, which we introduced in (2.17), to express the latter property of $\boldsymbol{\mathsf{M}}^{({l})}$![]() in the following way:
in the following way:
with $p > 1$![]() and, by definition, $p + q + r = l$
and, by definition, $p + q + r = l$![]() . This becomes plausible when an example is considered, e.g. $l = 5$
. This becomes plausible when an example is considered, e.g. $l = 5$![]() and $p = 2, q = 1$
and $p = 2, q = 1$![]() and $r = 2$
and $r = 2$![]() ,
,
Note that we used the symmetry of ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() . An immediate consequence of (4.1) is that we can express a multipole function with index $p > 1$
. An immediate consequence of (4.1) is that we can express a multipole function with index $p > 1$![]() as a sum of multipole functions with index $p - 2$
as a sum of multipole functions with index $p - 2$![]() . These, in turn, can again be expressed as a sum of multipole functions with index $p - 4$
. These, in turn, can again be expressed as a sum of multipole functions with index $p - 4$![]() . Depending on whether $p$
. Depending on whether $p$![]() is even or odd, this chain ends when $p = 0$
is even or odd, this chain ends when $p = 0$![]() or $p = 1$
or $p = 1$![]() . This computation can be represented in the form of Pascal's triangle (see figure 1). Note the alternating minus sign. Or, more compactly, in the following formula:
. This computation can be represented in the form of Pascal's triangle (see figure 1). Note the alternating minus sign. Or, more compactly, in the following formula:


Figure 1. Dependence of the multipole functions with $p > 1$![]() on functions with smaller $p$
on functions with smaller $p$![]() given by Pascal's triangle.
given by Pascal's triangle.
We can split the sum in (3.31) into even and odd $p$![]() values and plug in the expression for the multipole functions, which we just derived. This yields
values and plug in the expression for the multipole functions, which we just derived. This yields

The limits of the sums are
In a last step, we note that we can exchange the two sums. For example, for even $p$![]() , we find
, we find

The same holds true for odd $p$![]() . We arrive at the final result of this section, namely
. We arrive at the final result of this section, namely

For $m \geq ~0$![]() and with the coefficients
and with the coefficients

the solid harmonics with $m < 0$![]() can be computed with the formula $Y^{-m}_{l} = (-1)^{m}{Y^{m}_{l}}^{*}$
can be computed with the formula $Y^{-m}_{l} = (-1)^{m}{Y^{m}_{l}}^{*}$![]() .
.
We thus have a way to express an arbitrary solid harmonic of degree $l$![]() and order $m$
and order $m$![]() as a linear combination of the multipole basis functions with degree $l$
as a linear combination of the multipole basis functions with degree $l$![]() . We call the coefficients $\beta ^{m}_{l,0,k}$
. We call the coefficients $\beta ^{m}_{l,0,k}$![]() and $\beta ^{m}_{l,1,k}$
and $\beta ^{m}_{l,1,k}$![]() the basis transformation between the solid harmonics and the multipole basis functions in the space of homogeneous and harmonic polynomials of degree $l$
the basis transformation between the solid harmonics and the multipole basis functions in the space of homogeneous and harmonic polynomials of degree $l$![]() .
.
Last, but not least, the complex conjugate of the basis transformation relates the spherical multipole moments with the Cartesian multipole moments. A practical implication of this section's considerations is that it is only necessary to compute $2l + 1$![]() components of the Cartesian multipole moments (those corresponding to the multipole basis functions given in (2.18)) instead of the $(l + 2)(l + 1)/2$
components of the Cartesian multipole moments (those corresponding to the multipole basis functions given in (2.18)) instead of the $(l + 2)(l + 1)/2$![]() components of the symmetric tensor $\boldsymbol{\mathsf{Q}}^{({l})}$
components of the symmetric tensor $\boldsymbol{\mathsf{Q}}^{({l})}$![]() . A way to reconstruct the dependent components of $\boldsymbol{\mathsf{M}}^{({l})}$
. A way to reconstruct the dependent components of $\boldsymbol{\mathsf{M}}^{({l})}$![]() (or $\boldsymbol{\mathsf{Q}}^{({l})}$
(or $\boldsymbol{\mathsf{Q}}^{({l})}$![]() ) will be found in the next section while deriving the inverse basis transformation.
) will be found in the next section while deriving the inverse basis transformation.
5. Inverse transformation
We derive the inverse of the basis transformation given in (4.7) by, first, collecting the coefficients $\beta ^{m}_{l,0,k}$![]() and $\beta ^{m}_{l,1,k}$
and $\beta ^{m}_{l,1,k}$![]() in a matrix, the basis transformation matrix $\boldsymbol{\mathsf{B}}$
in a matrix, the basis transformation matrix $\boldsymbol{\mathsf{B}}$![]() , and second, by inverting this matrix.
, and second, by inverting this matrix.
How difficult it is to invert a matrix depends on its structure, e.g. if it is a diagonal matrix, computing the inverse consists in taking the reciprocal of its elements. The structure of the matrix $\boldsymbol{\mathsf{B}}$![]() simplifies if we use real spherical harmonics instead of Laplace's spherical harmonics.
simplifies if we use real spherical harmonics instead of Laplace's spherical harmonics.
The real spherical harmonics are defined as

Henceforth, we denote the above matrix by $\boldsymbol{\mathsf{S}}$![]() . Note that $\boldsymbol{\mathsf{S}}$
. Note that $\boldsymbol{\mathsf{S}}$![]() is unitary, i.e. $\boldsymbol{\mathsf{S}}^{{\dagger} }\boldsymbol{\mathsf{S}} = \boldsymbol{\mathsf{1}}$
is unitary, i.e. $\boldsymbol{\mathsf{S}}^{{\dagger} }\boldsymbol{\mathsf{S}} = \boldsymbol{\mathsf{1}}$![]() . An explicit expression for the real spherical harmonics is
. An explicit expression for the real spherical harmonics is
with $m \geq 0$![]() . Furthermore, the above definition implies the normalisation $N_{lm} \equiv \sqrt {2 - \delta _{m0}} N^{m}_{l}$
. Furthermore, the above definition implies the normalisation $N_{lm} \equiv \sqrt {2 - \delta _{m0}} N^{m}_{l}$![]() .
.
Applying the unitary transformation to (4.7) results in the following pattern:

This pattern has two implications for the structure of the basis transformation matrix $\boldsymbol{\mathsf{B}}$![]() . First, the unitary transformation brings it into a form in which it consists of four blocks which correspond to the above four cases. Second, since the limits of the sums $a$
. First, the unitary transformation brings it into a form in which it consists of four blocks which correspond to the above four cases. Second, since the limits of the sums $a$![]() and $b$
and $b$![]() decrease with decreasing $m$
decrease with decreasing $m$![]() , the corresponding real solid harmonic depends on less multipole basis functions. For example, let us consider the case $s = 0$
, the corresponding real solid harmonic depends on less multipole basis functions. For example, let us consider the case $s = 0$![]() and even $m$
and even $m$![]() for $l = 5$
for $l = 5$![]() . The even values of $m$
. The even values of $m$![]() are zero, two and four. The corresponding limits $a$
are zero, two and four. The corresponding limits $a$![]() are zero, one and two,respectively. Hence, the real solid harmonic of degree five and order zero depends on one multipole basis function, the one with order two on two and the last one with order four on three multipole basis functions. This pattern translates into a triangular matrix block. Hence, the basis transformation matrix can be transformed into a matrix, which consists of four triangular matrix blocks.
are zero, one and two,respectively. Hence, the real solid harmonic of degree five and order zero depends on one multipole basis function, the one with order two on two and the last one with order four on three multipole basis functions. This pattern translates into a triangular matrix block. Hence, the basis transformation matrix can be transformed into a matrix, which consists of four triangular matrix blocks.
Whether the triangular matrices show up also depends on the ordering of the solid harmonics and the multipole basis functions. For the solid harmonics, we pick the ordering, which is implicitly suggested by (5.1), namely
Additionally, a corresponding ordering for the multipole basis functions, for example, is
Assembling the matrix $\boldsymbol{\mathsf{B}}$![]() in accordance with these orderings brings (4.7) into the compact form:
in accordance with these orderings brings (4.7) into the compact form:
This equation can be multiplied with the unitary matrix $\boldsymbol{\mathsf{S}}$![]() . On the left-hand side, the real solid harmonics will show up and on the right-hand side, a matrix with the four blocks, which we found in (5.3). If we now re-order the real solid harmonics (and the multipole basis functions) such that the harmonics with even order $m$
. On the left-hand side, the real solid harmonics will show up and on the right-hand side, a matrix with the four blocks, which we found in (5.3). If we now re-order the real solid harmonics (and the multipole basis functions) such that the harmonics with even order $m$![]() (and odd order $m$
(and odd order $m$![]() ) are grouped together, four triangular matrices result. If we additionally reverse the order of the real solid harmonics with $s = 1$
) are grouped together, four triangular matrices result. If we additionally reverse the order of the real solid harmonics with $s = 1$![]() , we get four upper triangular matrices. Let $\boldsymbol{\mathsf{P}}$
, we get four upper triangular matrices. Let $\boldsymbol{\mathsf{P}}$![]() denote the corresponding permutation matrix, then
denote the corresponding permutation matrix, then
An actual computation for even $l$![]() shows the following matrix structure:
shows the following matrix structure:

For odd $l$![]() , the four upper triangular matrices are at other positions in the matrix.
, the four upper triangular matrices are at other positions in the matrix.
The inversion of this matrix is equivalent to inverting four upper triangular matrices. This can, for example, be done by applying repeatedly back-substitution with unit vectors as the right-hand sides (Press et al. Reference Press, Teukolsky, Vetterling and Flannery2007, § 2.2.1). We define the inverse basis transformation matrix as
Thus, $\boldsymbol {M}^{l} = r^{l} \boldsymbol{\mathsf{A}} \boldsymbol {Y}^{l}$![]() and with the help of a suitable mapping between the matrix indices and the $p,q,r$
and with the help of a suitable mapping between the matrix indices and the $p,q,r$![]() indices, we get
indices, we get

We call the $\alpha ^{m}_{l,0,q,r}$![]() and $\alpha ^{m}_{l,1,q,r}$
and $\alpha ^{m}_{l,1,q,r}$![]() the inverse basis transformation.
the inverse basis transformation.
The dependent multipole functions (i.e. the functions with index $p > 1$![]() ) can be expressed as a linear combination of the multipole basis functions (see (4.3)). Since the multipole basis functions are $\boldsymbol {M}^{l} = r^{l}\boldsymbol{\mathsf{A}}\boldsymbol {Y}^{l}$
) can be expressed as a linear combination of the multipole basis functions (see (4.3)). Since the multipole basis functions are $\boldsymbol {M}^{l} = r^{l}\boldsymbol{\mathsf{A}}\boldsymbol {Y}^{l}$![]() , it is possible to obtain an expression for the dependent multipole functions in terms of the solid harmonics by adding the rows of the inverse basis transformation matrix while multiplying them by the factor given in (4.3).
, it is possible to obtain an expression for the dependent multipole functions in terms of the solid harmonics by adding the rows of the inverse basis transformation matrix while multiplying them by the factor given in (4.3).
The relation between the (independent) Cartesian multipole moments and the spherical multipole moments is given by the complex conjugate of the inverse basis transformation (matrix), i.e.
Last, but not least, instead of inverting the basis transformation matrix $\boldsymbol{\mathsf{B}}$![]() , it is possible to directly compute the inverse basis transformation matrix $\boldsymbol{\mathsf{A}}$
, it is possible to directly compute the inverse basis transformation matrix $\boldsymbol{\mathsf{A}}$![]() . A derivation of the formulae for the $\alpha$
. A derivation of the formulae for the $\alpha$![]() s is provided in Appendix C.
s is provided in Appendix C.
6. The Vlasov–Fokker–Planck equation
In this section, we come back to the original problem, which stood at the beginning of our investigation of the relation between the Cartesian multipole moments and the spherical multipole moments: the two expansions of the distribution function $f$![]() and their relation.
and their relation.
In the first step, we show that their relation is the same as the relation between the Cartesian multipole moments and spherical multipole moments. To this end, we investigate the differences between (2.9) and (2.21) and the expansions of $f$![]() given in (1.3) and (1.2). The expansions of $f$
given in (1.3) and (1.2). The expansions of $f$![]() are done in momentum space (and not in configuration space), the coefficients (previously ${\mathsf{Q}}^{({l})}_{i_{1} \ldots i_{l}}$
are done in momentum space (and not in configuration space), the coefficients (previously ${\mathsf{Q}}^{({l})}_{i_{1} \ldots i_{l}}$![]() and $q^{m}_{l}$
and $q^{m}_{l}$![]() and now ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
and now ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() and $f^{m}_{l}$
and $f^{m}_{l}$![]() ) are functions, there are no numerical factors and, most importantly, the magnitude of $\boldsymbol {p}$
) are functions, there are no numerical factors and, most importantly, the magnitude of $\boldsymbol {p}$![]() (previously $\boldsymbol {r}$
(previously $\boldsymbol {r}$![]() ) was set to one. This last difference accounts for the factor $p^{-l}$
) was set to one. This last difference accounts for the factor $p^{-l}$![]() in (1.3), since $\boldsymbol {p}/p$
in (1.3), since $\boldsymbol {p}/p$![]() restricts the components of $\boldsymbol {p}$
restricts the components of $\boldsymbol {p}$![]() to the unit sphere in momentum space. The dependence on the magnitude of $p$
to the unit sphere in momentum space. The dependence on the magnitude of $p$![]() is now included in the coefficients $f^{m}_{l}$
is now included in the coefficients $f^{m}_{l}$![]() and not explicitly given as $1/r^{2~l + 1}$
and not explicitly given as $1/r^{2~l + 1}$![]() .
.
The fact that the coefficients ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() and $f^{m}_{l}$
and $f^{m}_{l}$![]() are functions does not change the relation between them. Actually, the object ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
are functions does not change the relation between them. Actually, the object ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() is constructed (for example, it is chosen to be symmetric in its indices and it should be chosen to be traceless as well) such that the relation between it and the $f^{m}_{l}$
is constructed (for example, it is chosen to be symmetric in its indices and it should be chosen to be traceless as well) such that the relation between it and the $f^{m}_{l}$![]() s is the same as between the Cartesian multipole moments and the spherical multipole moments. The fact that $p$
s is the same as between the Cartesian multipole moments and the spherical multipole moments. The fact that $p$![]() (or $r$
(or $r$![]() ) was set to one also does not change the relation. This can be seen by setting $r$
) was set to one also does not change the relation. This can be seen by setting $r$![]() to one and restricting the magnitude of $\boldsymbol {r}$
to one and restricting the magnitude of $\boldsymbol {r}$![]() to one in (5.6). However, that there are no factors means that $4{\rm \pi} /(2~l + 1)$
to one in (5.6). However, that there are no factors means that $4{\rm \pi} /(2~l + 1)$![]() was included in the definition of $f^{m}_{l}$
was included in the definition of $f^{m}_{l}$![]() (see (2.22)) and $1/l!$
(see (2.22)) and $1/l!$![]() is included in the definition of ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
is included in the definition of ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() (cf. with (2.7)). Thus, the relation is given by (5.11a,b), i.e.
(cf. with (2.7)). Thus, the relation is given by (5.11a,b), i.e.
where we replaced $\boldsymbol {q}^{l}$![]() with $\boldsymbol {f}^{l}$
with $\boldsymbol {f}^{l}$![]() , $\boldsymbol {Q}^{l}$
, $\boldsymbol {Q}^{l}$![]() with $\boldsymbol {F}^{l}$
with $\boldsymbol {F}^{l}$![]() , and multiplied with $\boldsymbol{\mathsf{D}}_{1} \equiv 4{\rm \pi} /(2l + 1) {1}$
, and multiplied with $\boldsymbol{\mathsf{D}}_{1} \equiv 4{\rm \pi} /(2l + 1) {1}$![]() and $\boldsymbol{\mathsf{D}}_{2} \equiv l! {1}$
and $\boldsymbol{\mathsf{D}}_{2} \equiv l! {1}$![]() to include the factors in the definitions of the coefficients. The inverse transformation is obtained by computing the inverse of the above matrix, as explained in § 5.
to include the factors in the definitions of the coefficients. The inverse transformation is obtained by computing the inverse of the above matrix, as explained in § 5.
Johnston (Reference Johnston1960) derives this inverse basis transformation for $l = 2$![]() and $l = 3$
and $l = 3$![]() . However, when expanding $f$
. However, when expanding $f$![]() , he uses the real spherical harmonics without normalisation $N_{lm}$
, he uses the real spherical harmonics without normalisation $N_{lm}$![]() and without including $(-1)^{m}$
and without including $(-1)^{m}$![]() in the definition of the associated Legendre polynomials. Thus, he implicitly starts with the following equation:
in the definition of the associated Legendre polynomials. Thus, he implicitly starts with the following equation:

The fraction with factorials appears because the numerical factor in the addition theorem changes if (real) spherical harmonics without normalisation are used to derive it (cf. with (2.20)). Moreover, $1/N_{lm}$![]() removes the normalisation. Additionally, in the last definition of (6.2), all these factors are included in the coefficients $f_{lms}$
removes the normalisation. Additionally, in the last definition of (6.2), all these factors are included in the coefficients $f_{lms}$![]() .
.
Thus, we should be able to reproduce his results by inverting the matrix on the right-hand side of
which yields the following matrix:
where $\boldsymbol{\mathsf{A}}^{*} = {\boldsymbol{\mathsf{B}}^{*}}^{-1}$![]() and where we introduced the following definitions:
and where we introduced the following definitions:

Furthermore, $\boldsymbol{\mathsf{S}}$![]() is the unitary transformation between Laplace's spherical harmonics and the real spherical harmonics (see (5.2)). The complex conjugate is necessary, because we are using the complex conjugate of (5.6) (namely, we are using ${Y^{m}_{l}}^{*}$
is the unitary transformation between Laplace's spherical harmonics and the real spherical harmonics (see (5.2)). The complex conjugate is necessary, because we are using the complex conjugate of (5.6) (namely, we are using ${Y^{m}_{l}}^{*}$![]() and comparing with (5.11a,b)). The dependent components of ${\mathsf{F}}^{l}_{i_{1} \ldots i_{l}}$
and comparing with (5.11a,b)). The dependent components of ${\mathsf{F}}^{l}_{i_{1} \ldots i_{l}}$![]() can be computed as described at the end of § 5. The entries of the matrix $\boldsymbol{\mathsf{A}}_{{J}}$
can be computed as described at the end of § 5. The entries of the matrix $\boldsymbol{\mathsf{A}}_{{J}}$![]() can be compared with (9a–d) in the paper by Johnston (Reference Johnston1960). Moreover, the entries of $\boldsymbol{\mathsf{A}}^{*}$
can be compared with (9a–d) in the paper by Johnston (Reference Johnston1960). Moreover, the entries of $\boldsymbol{\mathsf{A}}^{*}$![]() can be directly computed with formulae derived in Appendix C.
can be directly computed with formulae derived in Appendix C.
Last, but not least, the Vlasov–Fokker–Planck equation and the corresponding expansions of $f$![]() can be considered as an example partial differential equation (PDE). We note that whenever (Laplace's) spherical harmonics are used to expand a solution to a PDE, it is possible to work with the multipole functions instead (or vice versa). If the multipole functions are used, it is always enough to compute the $2l + 1$
can be considered as an example partial differential equation (PDE). We note that whenever (Laplace's) spherical harmonics are used to expand a solution to a PDE, it is possible to work with the multipole functions instead (or vice versa). If the multipole functions are used, it is always enough to compute the $2l + 1$![]() independent components, namely the multipole basis functions.
independent components, namely the multipole basis functions.
7. Conclusion
We started off with the aim to find a way to convert between the coefficients appearing in the Cartesian tensor expansion and the spherical harmonic expansion of the distribution function $f$![]() . A problem which was prominently investigated by Johnston (Reference Johnston1960).
. A problem which was prominently investigated by Johnston (Reference Johnston1960).
We pointed out that the relation between the Cartesian tensors $\boldsymbol{\mathsf{F}}^{({l})}$![]() and the $f^{m}_{l}$
and the $f^{m}_{l}$![]() is the same as the relation between the Cartesian multipole moments $\boldsymbol{\mathsf{Q}}^{({l})}$
is the same as the relation between the Cartesian multipole moments $\boldsymbol{\mathsf{Q}}^{({l})}$![]() and the spherical multipole moments $q^{m}_{l}$
and the spherical multipole moments $q^{m}_{l}$![]() . Since multipole moments are ubiquitous in physics, we revisited the problem of converting between coefficients of expansions in the context of the multipole expansion.
. Since multipole moments are ubiquitous in physics, we revisited the problem of converting between coefficients of expansions in the context of the multipole expansion.
In the first step, we introduced a new definition of the Cartesian multipole moments and showed that it reproduces the known multipole moments. We saw that this definition contained the multipole functions ${\mathsf{M}}^{({l})}_{i_{1} \ldots i_{l}}$![]() , which are proven to be homogeneous and harmonic polynomials of degree $l$
, which are proven to be homogeneous and harmonic polynomials of degree $l$![]() . Furthermore, we pointed out that a subset of the multipole functions is a basis of the space of homogeneous and harmonic polynomials $\mathcal {H}^{l}(\mathbb {R}^{3})$
. Furthermore, we pointed out that a subset of the multipole functions is a basis of the space of homogeneous and harmonic polynomials $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() . We called this subset the multipole basis functions.
. We called this subset the multipole basis functions.
Subsequently, we took a look at the definition of the spherical multipole moments and noticed that it contains the complex conjugate of a solid harmonic of degree $l$![]() and order $m$
and order $m$![]() . We showed that these functions are also harmonic and homogeneous polynomials of degree $l$
. We showed that these functions are also harmonic and homogeneous polynomials of degree $l$![]() and that they are a basis of $\mathcal {H}^{l}(\mathbb {R}^{3})$
and that they are a basis of $\mathcal {H}^{l}(\mathbb {R}^{3})$![]() as well.
as well.
This led us to the new conclusion that the relation between the Cartesian multipole moments and the spherical multipole moments can be formalised as a basis transformation between the solid harmonics of degree $l$![]() and the multipole basis functions of degree $l$
and the multipole basis functions of degree $l$![]() .
.
We derived closed-form formulae to compute the basis transformation, i.e. we derived a way to express the solid harmonics of degree $l$![]() and order $m \geq 0$
and order $m \geq 0$![]() as a sum of multipole basis functions. We inverted the basis transformation matrix and simplified the computation of the inverse matrix considerably. Additionally, we also derived closed-form formulae for the inverse basis transformation (see Appendix C). We, thus, provided a systematic and easy-to-compute method to convert between the Cartesian multipole moments and the spherical multipole moments.
as a sum of multipole basis functions. We inverted the basis transformation matrix and simplified the computation of the inverse matrix considerably. Additionally, we also derived closed-form formulae for the inverse basis transformation (see Appendix C). We, thus, provided a systematic and easy-to-compute method to convert between the Cartesian multipole moments and the spherical multipole moments.
A key practical implication of our approach is the insight, that it is enough to compute $2\,l + 1$![]() components of the Cartesian multipole moments, namely the components corresponding to the multipole basis functions. The dependent components can be computed as explained at the end of § 5.
components of the Cartesian multipole moments, namely the components corresponding to the multipole basis functions. The dependent components can be computed as explained at the end of § 5.
Eventually, we came back to our original problem and applied our knowledge about the relation between the Cartesian multipole moments and the spherical multipole moments in the context of the Cartesian tensor and the spherical harmonic expansion of $f$![]() . We used the basis transformation matrix $\boldsymbol{\mathsf{B}}$
. We used the basis transformation matrix $\boldsymbol{\mathsf{B}}$![]() to express the coefficients $\,f^{m}_{l}$
to express the coefficients $\,f^{m}_{l}$![]() as a linear combination of the independent components of the corresponding Cartesian tensor ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$
as a linear combination of the independent components of the corresponding Cartesian tensor ${\mathsf{F}}^{({l})}_{i_{1} \ldots i_{l}}$![]() . We explained how our results reproduce the findings in Johnston (Reference Johnston1960).
. We explained how our results reproduce the findings in Johnston (Reference Johnston1960).
We developed a free and open-source command-line tool, called multipole-conv (Schween & Reville Reference Schween and Reville2022), which is able to compute the basis transformation matrix and its inverse. We hope that this tool will be useful for all who work with spherical harmonics or multipole moments.
Last, but not least, we would like to assess our approach critically. First, the elements in the basis transformation matrix $\boldsymbol{\mathsf{B}}$![]() become very small even for small $l$
become very small even for small $l$![]() , say $l \approx 15$
, say $l \approx 15$![]() , and the elements of the inverse basis transformation matrix $\boldsymbol{\mathsf{A}}$
, and the elements of the inverse basis transformation matrix $\boldsymbol{\mathsf{A}}$![]() very large. This leads to numerical errors in the computation of $\boldsymbol{\mathsf{A}}$
very large. This leads to numerical errors in the computation of $\boldsymbol{\mathsf{A}}$![]() . We suspect that this happens because Laplace's spherical harmonics are normalised whereas the multipole basis functions are not. Second, the mathematically inclined reader may know that Laplace's spherical harmonics are an irreducible representation of $SO(3)$
. We suspect that this happens because Laplace's spherical harmonics are normalised whereas the multipole basis functions are not. Second, the mathematically inclined reader may know that Laplace's spherical harmonics are an irreducible representation of $SO(3)$![]() . Since both definitions of the multipole basis functions, i.e. the definition with the Kelvin transform (see (2.17) and, in particular, (3.9)) and the definition with Efimov's ladder operator (cf. with (3.7)) generalise to arbitrary dimensions, it could be that there also exists a basis transformation between these generalised multipole basis functions and irreducible representations of $SO(n)$
. Since both definitions of the multipole basis functions, i.e. the definition with the Kelvin transform (see (2.17) and, in particular, (3.9)) and the definition with Efimov's ladder operator (cf. with (3.7)) generalise to arbitrary dimensions, it could be that there also exists a basis transformation between these generalised multipole basis functions and irreducible representations of $SO(n)$![]() .
.
Supplementary material
A free and open-source command-line tool, called multipole-conv, is available at https://github.com/nils-schween/multipole-conv.
Acknowledgements
We thank Professor J. Kirk and J. Kania for helpful discussions.
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Appendix A. Notes on the definition of the Cartesian multipole moments
A.1. The multipole moments are tensors
We would like to use our definition of Cartesian multipole moments, which is given in (2.7), to show that they are tensors. In the physics literature, a rank $l$![]() th tensor $\boldsymbol{\mathsf{T}}^{({l})}$
th tensor $\boldsymbol{\mathsf{T}}^{({l})}$![]() is defined as a quantity having $3^{l}$
is defined as a quantity having $3^{l}$![]() components ${\mathsf{T}}^{({l})}_{i_{1} \ldots i_{l}}$
components ${\mathsf{T}}^{({l})}_{i_{1} \ldots i_{l}}$![]() , which transform under coordinate transformations according to the following scheme (cf. Goldstein, Poole & Safko Reference Goldstein, Poole and Safko2014, p. 189):
, which transform under coordinate transformations according to the following scheme (cf. Goldstein, Poole & Safko Reference Goldstein, Poole and Safko2014, p. 189):
Our definition of the Cartesian multipole moments implies this, i.e.

Note that we dropped the primes in the definition of the Cartesian multipole moments to increase readability.
A.2. The $P$ operator
operator
We defined the ${P}$![]() operator implicitly using the description: ‘[It] produces the sum over the pairs of indices needed to assure symmetry’. We now give a more explicit definition.
operator implicitly using the description: ‘[It] produces the sum over the pairs of indices needed to assure symmetry’. We now give a more explicit definition.
${P}$![]() acts on a product of components of $\boldsymbol {r}$
acts on a product of components of $\boldsymbol {r}$![]() and Kronecker deltas, i.e.
and Kronecker deltas, i.e.
Note that there are $k$![]() Kronecker deltas and $l - 2k$
Kronecker deltas and $l - 2k$![]() components of $\boldsymbol {r}$
components of $\boldsymbol {r}$![]() .
.
The $P$![]() operator produces a sum of products, which must not change if arbitrary indices are exchanged, i.e. which is symmetric. Moreover, note that in each product, all indices are distinct (no index appears twice).
operator produces a sum of products, which must not change if arbitrary indices are exchanged, i.e. which is symmetric. Moreover, note that in each product, all indices are distinct (no index appears twice).
For $k = 0$![]() , we define
, we define
Note that a product is commutative, hence this (trivial) sum is symmetric. For $k = 1$![]() , one Kronecker delta is part of the products and the sum created by ${P}$
, one Kronecker delta is part of the products and the sum created by ${P}$![]() will be symmetric if it contains all the terms (products) with Kronecker deltas whose two indices correspond to all possible pairs, which can be formed from the $l$
will be symmetric if it contains all the terms (products) with Kronecker deltas whose two indices correspond to all possible pairs, which can be formed from the $l$![]() indices. For example, if $l = 3$
indices. For example, if $l = 3$![]() , then there are $\binom {3}{2} = 3$
, then there are $\binom {3}{2} = 3$![]() pairs of indices and accordingly,
pairs of indices and accordingly,
This guarantees the symmetry of the sum, because whenever an index of a Kronecker delta is exchanged with another index (may it be an index of a component of $\boldsymbol {r}$![]() or of another Kronecker delta), the newly created pair is matched by another term with a Kronecker delta whose pair of indices turns into the Kronecker delta's original combination of indices. Generally, if $k = 1$
or of another Kronecker delta), the newly created pair is matched by another term with a Kronecker delta whose pair of indices turns into the Kronecker delta's original combination of indices. Generally, if $k = 1$![]() , the sum produced by ${P}$
, the sum produced by ${P}$![]() contains $\binom {l}{2}$
contains $\binom {l}{2}$![]() terms.
terms.
The $k$![]() Kronecker deltas need to be equipped with $k$
Kronecker deltas need to be equipped with $k$![]() pairs of indices. Since no index appears twice in a product, the pairs must be distinct, or more technically, disjoint. We can collect all distinct pairs in a set. The ${P}$
pairs of indices. Since no index appears twice in a product, the pairs must be distinct, or more technically, disjoint. We can collect all distinct pairs in a set. The ${P}$![]() operator must produce a sum over all sets of distinct pairs of indices to make it symmetric. For example, if $l = 6$
operator must produce a sum over all sets of distinct pairs of indices to make it symmetric. For example, if $l = 6$![]() and $k = 2$
and $k = 2$![]() , the product $\delta _{i_{1}i_{2}}\delta _{i_{3}i_{4}}x_{i_{5}}x_{i_{6}}$
, the product $\delta _{i_{1}i_{2}}\delta _{i_{3}i_{4}}x_{i_{5}}x_{i_{6}}$![]() will be part of the sum. The set of distinct pairs is $\{(i_{1},i_{2}), (i_{3}, i_{4})\}$
will be part of the sum. The set of distinct pairs is $\{(i_{1},i_{2}), (i_{3}, i_{4})\}$![]() . If you exchange an index of one Kronecker delta with an index of the other, then a different set of distinct pairs is created. Additionally, to make the sum symmetric, another term whose set of distinct pairs (pertaining to the Kronecker deltas) matches the newly created set must be included in the sum. It is because a corresponding exchange of indices in the other term's set of pairs recreates the original one. Moreover, if you exchange an index of a Kronecker delta with an index of a component of $\boldsymbol {r}$
. If you exchange an index of one Kronecker delta with an index of the other, then a different set of distinct pairs is created. Additionally, to make the sum symmetric, another term whose set of distinct pairs (pertaining to the Kronecker deltas) matches the newly created set must be included in the sum. It is because a corresponding exchange of indices in the other term's set of pairs recreates the original one. Moreover, if you exchange an index of a Kronecker delta with an index of a component of $\boldsymbol {r}$![]() , a new set of distinct pairs is created, which also requires its counterpart to keep the sum symmetric. Hence, ${P}$
, a new set of distinct pairs is created, which also requires its counterpart to keep the sum symmetric. Hence, ${P}$![]() produces
produces

terms. The first factor counts the number of possible combinations of indices, which are then available to form sets of distinct pairs from them. The second factor counts the number of possible sets of distinct pairs. One way to approach the second factor is to think of a tennis tournament. In the first round, you have to think of who plays against whom and this is tantamount to build sets of distinct pairs. If you like to know how many sets there are, you can do the computation encoded in the second factor: choose two players from all the available players, then choose two players form the leftover players and so on. Since the order of the formed pairs is irrelevant, you divide by $k!$![]() (note that there are $k$
(note that there are $k$![]() pairs).
pairs).
Building the products in the sum, produced by the ${P}$![]() operator, can be done systematically. Assume there are $l$
operator, can be done systematically. Assume there are $l$![]() indices.
indices.
If you choose from them $2k$![]() indices, the possible combinations can be constructed as follows. Begin with $i_{1}$
indices, the possible combinations can be constructed as follows. Begin with $i_{1}$![]() , traverse the tree of possible combinations, which is determined by the other $l-1$
, traverse the tree of possible combinations, which is determined by the other $l-1$![]() indices and the amount of chosen indices, namely $2k$
indices and the amount of chosen indices, namely $2k$![]() . The pattern of this traversal is illustrated in the following example. In a next step, choose $i_{2}$
. The pattern of this traversal is illustrated in the following example. In a next step, choose $i_{2}$![]() and traverse the tree of possible combinations. However, this time, there are only $l-2$
and traverse the tree of possible combinations. However, this time, there are only $l-2$![]() indices left to form this tree; proceed until only one possibility is left. For example, $l = 6$
indices left to form this tree; proceed until only one possibility is left. For example, $l = 6$![]() and $k = 2$
and $k = 2$![]() , then
, then

are the possible combinations of indices.
In a second step, each combination has to be used to build sets of distinct pairs. Take for example the first combination $i_{1}i_{2}i_{3}i_{4}$![]() . The possible sets of distinct pairs are
. The possible sets of distinct pairs are
These sets were constructed by swapping the index $i_{2}$![]() with $i_{3}$
with $i_{3}$![]() and $i_{4}$
and $i_{4}$![]() . If it had not been four but six indices, the sets of distinct pairs would have been constructed by creating the above three sets with four indices and, subsequently, swapping one element of the leftover pair with all the indices appearing in the three sets. This process can be continued as needed. The terms in the sum corresponding to the above sets of distinct pairs are
. If it had not been four but six indices, the sets of distinct pairs would have been constructed by creating the above three sets with four indices and, subsequently, swapping one element of the leftover pair with all the indices appearing in the three sets. This process can be continued as needed. The terms in the sum corresponding to the above sets of distinct pairs are
The ${P}$![]() operator then sums over all sets of distinct pairs which are created for each of the above combination of indices.
operator then sums over all sets of distinct pairs which are created for each of the above combination of indices.
A.3. $c_{l,k}$ coefficients
coefficients
The coefficients $c_{l,k}$![]() appearing in the explicit expression for the multipole functions given in (2.14) can be computed. The multipole functions are harmonic polynomials, i.e. they are solutions to Laplace's equation. This implies that
appearing in the explicit expression for the multipole functions given in (2.14) can be computed. The multipole functions are harmonic polynomials, i.e. they are solutions to Laplace's equation. This implies that

The product rule tells us that
Hence, we calculate the following derivatives:

The first derivative is a straightforward computation. We explain the second and the third derivatives. We begin by replacing $R_{l,2k}$![]() in the second derivative with its definition, i.e.
in the second derivative with its definition, i.e.
Additionally, $\partial _{j} r^{2k} = 2k r^{2k - 2} x^{j}$![]() . The action of the derivative with respect to $x_{j}$
. The action of the derivative with respect to $x_{j}$![]() on the terms in the sum produced by the operator ${P}$
on the terms in the sum produced by the operator ${P}$![]() is most easily seen if an example term is considered, e.g.
is most easily seen if an example term is considered, e.g.
Here, $l - 2k$![]() terms appear. In every term, one of the components of $\boldsymbol {r}$
terms appear. In every term, one of the components of $\boldsymbol {r}$![]() is replaced with a Kronecker delta. Note that a contraction of the above sum with $x^{j}$
is replaced with a Kronecker delta. Note that a contraction of the above sum with $x^{j}$![]() yields $l - 2k$
yields $l - 2k$![]() times the original term. Whence,
times the original term. Whence,
To illuminate the reasoning behind the derivation of the third derivative, we again consider an example. Let $l = 6$![]() and $k = 0$
and $k = 0$![]() , then (by definition) ${P}$
, then (by definition) ${P}$![]() creates only one term, namely $x_{i_{1}} \ldots x_{i_{6}}$
creates only one term, namely $x_{i_{1}} \ldots x_{i_{6}}$![]() . If our expression for the third derivative is correct, applying the Laplace operator to this term yields the sum, which is created by $P$
. If our expression for the third derivative is correct, applying the Laplace operator to this term yields the sum, which is created by $P$![]() if $k = 1$
if $k = 1$![]() , times two. We can compute how many terms we expect this sum to have with the formula given in (A6), namely $\binom {6}{2} = 15$
, times two. We can compute how many terms we expect this sum to have with the formula given in (A6), namely $\binom {6}{2} = 15$![]() . Computing ${\rm \Delta} (x_{i_{1}} \ldots x_{i_{6}})$
. Computing ${\rm \Delta} (x_{i_{1}} \ldots x_{i_{6}})$![]() gives $30$
gives $30$![]() terms. However, for example,
terms. However, for example,
and
yield the same term if summed over $j$![]() . Hence, we get $15\times 2$
. Hence, we get $15\times 2$![]() terms and this is what we expect.
terms and this is what we expect.
If we apply the Laplace operator to ${P}$![]() when $k = 1$
when $k = 1$![]() , we expect to obtain the sum which is created by ${P}$
, we expect to obtain the sum which is created by ${P}$![]() when $k = 2$
when $k = 2$![]() times four. For $l = 6$
times four. For $l = 6$![]() and $k = 2$
and $k = 2$![]() , the ${P}$
, the ${P}$![]() operator produces a sum with $45$
operator produces a sum with $45$![]() terms. Applying $\varDelta$
terms. Applying $\varDelta$![]() to ${P}$
to ${P}$![]() when $k = 1$
when $k = 1$![]() , yields $15\times 4\times 3 = 180$
, yields $15\times 4\times 3 = 180$![]() terms. Note, this is exactly four times the amount of terms in $R_{4}$
terms. Note, this is exactly four times the amount of terms in $R_{4}$![]() . And, as the following example shows, the same term in ${\rm \Delta} R_{2}$
. And, as the following example shows, the same term in ${\rm \Delta} R_{2}$![]() appears four times, i.e.
appears four times, i.e.

Thus, we get the expected derivative.
This pattern can be generalised to arbitrary $l$![]() and $k$
and $k$![]() . The number of terms created when the Laplace operator is applied to $R_{2k}$
. The number of terms created when the Laplace operator is applied to $R_{2k}$![]() divided by the number of terms which are contained in the sum $R_{2k + 2}$
divided by the number of terms which are contained in the sum $R_{2k + 2}$![]() is
is

As in the above examples, ${\rm \Delta} R_{2k}$![]() includes $2k + 2$
includes $2k + 2$![]() times the same terms: two of them because of the components of $\boldsymbol {r}$
times the same terms: two of them because of the components of $\boldsymbol {r}$![]() (cf. with the first example) and two for each Kronecker delta (and there are $k$
(cf. with the first example) and two for each Kronecker delta (and there are $k$![]() of them). Thus,
of them). Thus,
The coefficients $c_{l,k}$![]() can be determined by plugging the three derivatives, given in (A12), into the equation presented at the beginning of this section, namely (A10). Collecting all factors in front of $r^{2k - 2}R_{2k}$
can be determined by plugging the three derivatives, given in (A12), into the equation presented at the beginning of this section, namely (A10). Collecting all factors in front of $r^{2k - 2}R_{2k}$![]() yields the following condition:
yields the following condition:
This condition implies the recurrence relation
Eventually, setting $c_{l,0} \equiv (2~l - 1)!!$![]() turns it into a closed-form expression:
turns it into a closed-form expression:
Appendix B. Commutator of the ladder operators
We would like to compute the commutator $[\mathrm {L}_{+}, {{D}}_{z}]$![]() . We use that $[\mathrm {L}_{i}, x^{j}] = \mathrm {i}\epsilon _{ijk}x^{k}$
. We use that $[\mathrm {L}_{i}, x^{j}] = \mathrm {i}\epsilon _{ijk}x^{k}$![]() and $[\mathrm {L}_{i}, \partial _{j}] = \mathrm {i}\epsilon _{ijk} \partial _{k}$
and $[\mathrm {L}_{i}, \partial _{j}] = \mathrm {i}\epsilon _{ijk} \partial _{k}$![]() (cf. Landau & Lifshitz Reference Landau and Lifshitz1977, p. 84, (26.4)–(5)) to compute
(cf. Landau & Lifshitz Reference Landau and Lifshitz1977, p. 84, (26.4)–(5)) to compute
and
where $\epsilon _{ijk}$![]() is the Levi–Civita symbol, which is, for example, defined in Jeevanjee (Reference Jeevanjee2011, p. 4, (1.1)). Since the commutator is linear, we get
is the Levi–Civita symbol, which is, for example, defined in Jeevanjee (Reference Jeevanjee2011, p. 4, (1.1)). Since the commutator is linear, we get
With the above formulae, we obtain for the last two terms

where we exploited that $\mathrm {L}_{+}$![]() does not contain a derivative with respect to $r$
does not contain a derivative with respect to $r$![]() (cf. (3.26)) and, hence, we could take $r^{2}$
(cf. (3.26)) and, hence, we could take $r^{2}$![]() out of the commutator. To compute the first term, we note that
out of the commutator. To compute the first term, we note that
where $A, B$![]() and $C$
and $C$![]() are arbitrary operators. Whence,
are arbitrary operators. Whence,

In the last step, we renamed the indices and used that the Levi–Civita symbol is antisymmetric, i.e. $\epsilon _{ijk} = - \epsilon _{ikj}$![]() . Using the last three results gives
. Using the last three results gives
Appendix C. Direct derivation of the inverse transformation
We derive a closed-form formula for the inverse basis transformation, namely for $\alpha ^{m}_{l,0,q,r}$![]() and $\alpha ^{m}_{l,1,q,r}$
and $\alpha ^{m}_{l,1,q,r}$![]() .
.
To this end, we use that (2.9) and (2.21) describe the same potential $\phi$![]() , i.e.
, i.e.

Moreover, at the end of § 3.1, we pointed out that the functions ${\mathsf{Q}}^{({l})}_{_{i_{1}} \ldots i_{l}}x^{i_{1}} \ldots x^{i_{l}}$![]() in the above multipole expansion are homogeneous and harmonic polynomials of degree $l$
in the above multipole expansion are homogeneous and harmonic polynomials of degree $l$![]() . The same is true for the solid harmonics $r^{l}Y^{m}_{l}$
. The same is true for the solid harmonics $r^{l}Y^{m}_{l}$![]() . This implies that
. This implies that

The factor $1/r^{2l + 1}$![]() cancels. We can use the notation introduced in (2.17) to express the left-hand side of the above equation as
cancels. We can use the notation introduced in (2.17) to express the left-hand side of the above equation as

The numerical factor in front of the Cartesian multipole moment ${\mathsf{Q}}^{({l})}_{pqr}$![]() reflects that the tensor $\boldsymbol{\mathsf{Q}}^{({l})}$
reflects that the tensor $\boldsymbol{\mathsf{Q}}^{({l})}$![]() is symmetric and that index combinations corresponding to specific values of $p, q$
is symmetric and that index combinations corresponding to specific values of $p, q$![]() and $r$
and $r$![]() appear more than once. Hence, (C2) becomes
appear more than once. Hence, (C2) becomes

The left-hand side of (C4) is a linear combination of the monomials $x^{p}y^{q}z^{r}$![]() with $p + q + r = l$
with $p + q + r = l$![]() . If we are able to express the sum of solid harmonics on the right-hand side of this equation as such a linear combination as well, we can equate coefficients to determine the ${\mathsf{Q}}^{({l})}_{pqr}$
. If we are able to express the sum of solid harmonics on the right-hand side of this equation as such a linear combination as well, we can equate coefficients to determine the ${\mathsf{Q}}^{({l})}_{pqr}$![]() . Since the factors in front of the solid harmonics are the spherical multipole moments $q^{m}_{l}$
. Since the factors in front of the solid harmonics are the spherical multipole moments $q^{m}_{l}$![]() , the components ${\mathsf{Q}}^{({l})}_{pqr}$
, the components ${\mathsf{Q}}^{({l})}_{pqr}$![]() of the Cartesian multipole moment must be a sum of them. Equation (4.3) informs us that we can express the components ${\mathsf{Q}}^{({l})}_{pqr}$
of the Cartesian multipole moment must be a sum of them. Equation (4.3) informs us that we can express the components ${\mathsf{Q}}^{({l})}_{pqr}$![]() with $p > 1$
with $p > 1$![]() as a sum of the components with $p = 0$
as a sum of the components with $p = 0$![]() or $p = 1$
or $p = 1$![]() . Thus, we can restrict our attention to the coefficients in front of the monomials with $p$
. Thus, we can restrict our attention to the coefficients in front of the monomials with $p$![]() equal to zero or $p$
equal to zero or $p$![]() equal to one. Furthermore, a look at (5.11a,b) tells us that these coefficients (which must be a sum of the spherical multipole moments) contain the complex conjugate of the $\alpha ^{m}_{l, 0, q, r}$
equal to one. Furthermore, a look at (5.11a,b) tells us that these coefficients (which must be a sum of the spherical multipole moments) contain the complex conjugate of the $\alpha ^{m}_{l, 0, q, r}$![]() and $\alpha ^{m}_{l, 1, q, r}$
and $\alpha ^{m}_{l, 1, q, r}$![]() . Hence, we proceed in two steps. First, we express the solid harmonics as a linear combination of monomials. Second, we isolate the $p = 0$
. Hence, we proceed in two steps. First, we express the solid harmonics as a linear combination of monomials. Second, we isolate the $p = 0$![]() or $p = 1$
or $p = 1$![]() part of this sum and, subsequently, equate coefficients.
part of this sum and, subsequently, equate coefficients.
Step one begins with (2.25), namely
and we use the following closed-form expression of the Legendre polynomials

to obtain

where the numerical factor $R^{m}_{l, j}$![]() is defined as
is defined as
In the next step, we rewrite the expression in parentheses using the binomial theorem. Furthermore, we apply the multinomial theorem to expand the factor $r^{2j}$![]() . This yields
. This yields

We finished step one: we found a way to write the solid harmonics as a linear combination of monomials.
We now isolate the part of the above sum where the exponent of $x$![]() , namely $p = k + 2i_{1}$
, namely $p = k + 2i_{1}$![]() , is either zero or one. Note that if $p = 0$
, is either zero or one. Note that if $p = 0$![]() , then $k = 0$
, then $k = 0$![]() and $i_{1} = 0$
and $i_{1} = 0$![]() . Additionally, since $i_{1} + i_{2} + i_{3} = j$
. Additionally, since $i_{1} + i_{2} + i_{3} = j$![]() , the last statement implies that $i_{3} = j - i_{2}$
, the last statement implies that $i_{3} = j - i_{2}$![]() . We conclude that the $p = 0$
. We conclude that the $p = 0$![]() part of the sum is
part of the sum is

In the last line, we relabelled the index $i_{2}$![]() to $k$
to $k$![]() . Since we would like to equate the coefficients in front of the monomials, we should reorder the above sum such that all coefficients in front of monomials with specific values of $q = m + 2k$
. Since we would like to equate the coefficients in front of the monomials, we should reorder the above sum such that all coefficients in front of monomials with specific values of $q = m + 2k$![]() and $r = l - m - 2k$
and $r = l - m - 2k$![]() are summed. The result of this reordering is
are summed. The result of this reordering is

When isolating the $p = 1$![]() part of the sum in (C9), we get
part of the sum in (C9), we get

Thus, we isolated the $p = 0$![]() and $p = 1$
and $p = 1$![]() parts of the expression for a solid harmonic in terms of monomials.
parts of the expression for a solid harmonic in terms of monomials.
Before we use (C4) to determine the components ${\mathsf{Q}}^{({l})}_{pqr}$![]() via equating the coefficients of the two polynomials, we rewrite the right-hand side of this equation as follows:
via equating the coefficients of the two polynomials, we rewrite the right-hand side of this equation as follows:

This equation in conjunction with (C11) implies for the $p = 0$![]() part of the sums on both sides of it that
part of the sums on both sides of it that

In the second line, we once more reordered the sum such that all coefficients in front of the monomials with the same exponents were grouped together. This implies

for $q \in \{0, 1, \ldots, l\}$![]() and where the complex conjugate inverse basis transformation is defined as
and where the complex conjugate inverse basis transformation is defined as

Note that $\alpha ^{*-(q-2k)}_{l,0,q,(l-q)} = \alpha ^{*q-2k}_{l,0,q,(l-q)}$![]() .
.
The above computation can be repeated for the $p = 1$![]() part of the sums with (C12). This leads to
part of the sums with (C12). This leads to

for $q \in \{0, \ldots, l-1\}$![]() with
with

Moreover, $\alpha ^{*-(q + 1 - 2k)}_{l,1,q,(l-q)} = -\alpha ^{*q + 1 - 2k}_{l,1,q,(l-q)}$![]() .
.
The presented formulae for the $\alpha$![]() terms allow a computation of the inverse basis transformation matrix $\boldsymbol{\mathsf{A}}$
terms allow a computation of the inverse basis transformation matrix $\boldsymbol{\mathsf{A}}$![]() without inverting the basis transformation matrix $\boldsymbol{\mathsf{B}}$
without inverting the basis transformation matrix $\boldsymbol{\mathsf{B}}$![]() . The arguments to derive the formulae are an adaptation of findings by Johnston (Reference Johnston1960) to our insight that only the components of ${\mathsf{Q}}^{({l})}_{pqr}$
. The arguments to derive the formulae are an adaptation of findings by Johnston (Reference Johnston1960) to our insight that only the components of ${\mathsf{Q}}^{({l})}_{pqr}$![]() with $p \leq ~1$
with $p \leq ~1$![]() are needed.
are needed.