Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-17T16:20:09.521Z Has data issue: false hasContentIssue false
  • English
  • Français

An adjoint method for neoclassical stellarator optimization

Part of: Focus on Fusion

Published online by Cambridge University Press:  06 September 2019

Elizabeth J. Paul Open the ORCID record for Elizabeth J. Paul [Opens in a new window] ,
Ian G. Abel Open the ORCID record for Ian G. Abel [Opens in a new window] ,
Matt Landreman Open the ORCID record for Matt Landreman [Opens in a new window]  and
William Dorland Open the ORCID record for William Dorland [Opens in a new window]
Elizabeth J. Paul*
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD 20742, USA
Ian G. Abel
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD 20742, USA Department of Physics, Chalmers University of Technology, Göteborg, SE-41296, Sweden
Matt Landreman
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD 20742, USA
William Dorland
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: ejpaul@umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Stellarators are a promising route to steady-state fusion power. However, to achieve the required confinement, the magnetic geometry must be highly optimized. This optimization requires navigating high-dimensional spaces, often necessitating the use of gradient-based methods. The gradient of the neoclassical fluxes is expensive to compute with classical methods, requiring 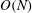$O(N)$ flux computations, where $N$ is the number of parameters. To reduce the cost of the gradient computation, we present an adjoint method for computing the derivatives of moments of the neoclassical distribution function for stellarator optimization. The linear adjoint method allows derivatives of quantities which depend on solutions of a linear system, such as moments of the distribution function, to be computed with respect to many parameters from the solution of only two linear systems. This reduces the cost of computing the gradient to the point that the finite-collisionality neoclassical fluxes can be used within an optimization loop. With the neoclassical adjoint method, we compute solutions of the drift kinetic equation and an adjoint drift kinetic equation to obtain derivatives of neoclassical quantities with respect to geometric parameters. When the number of parameters in the derivative is large (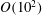$O(10^{2})$), this adjoint method provides up to a factor of 200 reduction in cost. We demonstrate adjoint-based optimization of the field strength to obtain minimal bootstrap current on a surface. With adjoint-based derivatives, we also compute the local sensitivity to magnetic perturbations on a flux surface and identify regions where tight tolerances on error fields are required for control of the bootstrap current or radial transport. Furthermore, the solve for the ambipolar electric field is accelerated using a Newton method with derivatives obtained from the adjoint method.

Keywords

fusion plasmaplasma confinementplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 5 , October 2019 , 795850501
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abel, I., Plunk, G., Wang, E., Barnes, M., Cowley, S., Dorland, W. & Schekochihin, A. 2013 Multiscale gyrokinetics for rotating tokamak plasmas: fluctuations, transport and energy flows. Rep. Prog. Phys. 76 (11), 116201.Google Scholar
Allaire, G., De Gournay, F., Jouve, F. & Toader, A.-M. 2005 Structural optimization using topological and shape sensitivity via a level set method. Control and Cybernetics 34 (1), 59.Google Scholar
Antonsen, T., Paul, E. J. & Landreman, M. 2019 Adjoint approach to calculating shape gradients for three-dimensional magnetic confinement equilibria. J. Plasma Phys. 85 (2), 905850207.Google Scholar
Barnes, M., Abel, I., Dorland, W., Görler, T., Hammett, G. & Jenko, F. 2010 Direct multiscale coupling of a transport code to gyrokinetic turbulence codes. Phys. Plasmas 17 (5), 056109.Google Scholar
Beidler, C., Allmaier, K., Isaev, M. Y., Kasilov, S., Kernbichler, W., Leitold, G., Maaßberg, H., Mikkelsen, D., Murakami, S., Schmidt, M. et al. 2011 Benchmarking of the mono-energetic transport coefficientsresults from the International Collaboration on Neoclassical Transport in Stellarators (ICNTS). Nucl. Fusion 51 (7), 076001.Google Scholar
Beidler, C., Grieger, G., Herrnegger, F., Harmeyer, E., Lotz, W., Maassberg, H., Merkel, P., Nührenberg, J., Rau, F., Sapper, J. et al. 1990 Physics and engineering design for Wendelstein VII-X. Fusion Technol. 17 (1), 148–168.Google Scholar
Beidler, C. D. & D’haeseleer, W. D. 1995 A general solution of the ripple-averaged kinetic equation (GSRAKE). Plasma Phys. Control. Fusion 37 (4), 463.Google Scholar
Belli, E. A. & Candy, J. 2015 Neoclassical transport in toroidal plasmas with nonaxisymmetric flux surfaces. Plasma Phys. Control. Fusion 57 (5), 054012.Google Scholar
Brent, R. P. 2013 Algorithms for Minimization without Derivatives. Courier Corporation.Google Scholar
Calvo, I., Velasco, J. L., Parra, F. I., Alonso, J. A. & García-Regaña, J. M. 2018 Electrostatic potential variations on stellarator magnetic surfaces in low collisionality regimes. J. Plasma Phys. 84 (4), 905840407.Google Scholar
Dekeyser, W., Reiter, D. & Baelmans, M. 2014a Automated divertor target design by adjoint shape sensitivity analysis and a one-shot method. J. Comput. Phys. 278, 117–132.Google Scholar
Dekeyser, W., Reiter, D. & Baelmans, M. 2014b A one shot method for divertor target shape optimization. Proc. Appl. Maths Mech. 14 (1), 1017–1022.Google Scholar
Dekeyser, W., Reiter, D. & Baelmans, M. 2014c Optimal shape design for divertors. Intl J. Comput. Sci. Eng. 2 9 (5–6), 397–407.Google Scholar
Delfour, M. C. & Zolâsio, J.-P. 2011 Shapes and Geometries: Metrics, Analysis, Differential Calculus, and Optimization, Advances in Design and Control, vol. 22, chap. 2. SIAM.Google Scholar
Delfour, M. C. & Zolésio, J.-P. 2011 Shapes and Geometries: Metrics, Analysis, Differential Calculus, and Optimization, Advances in Design and Control, vol. 22, chap. 9. SIAM.Google Scholar
Fichtner, A., Bunge, H.-P. & Igel, H. 2006 The adjoint method in seismology: I. Theory. Phys. Earth Planet. Inter. 157 (1–2), 86–104.Google Scholar
Garren, D. & Boozer, A. H. 1991 Existence of quasihelically symmetric stellarators. Phys. Fluids B 3 (10), 2822–2834.Google Scholar
Gibson, A. & Taylor, J. B. 1967 Single particle motion in toroidal stellarator fields. Phys. Fluids 10 (12), 2653–2659.Google Scholar
Glowinski, R. & Pironneau, O. 1975 On the numerical computation of the minimum-drag profile in laminar flow. J. Fluid Mech. 72 (2), 385.Google Scholar
Grieger, G., Lotz, W., Merkel, P., Nührenberg, J., Sapper, J., Strumberger, E., Wobig, H., Burhenn, R., Erckmann, V., Gasparino, U. et al. 1992 Physics optimization of stellarators. Phys. Fluids B 4 (7), 2081–2091.Google Scholar
Hastings, D., Houlberg, W. & Shaing, K.-C. 1985 The ambipolar electric field in stellarators. Nucl. Fusion 25 (4), 445.Google Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77 (8), 087001.Google Scholar
Helander, P., Parra, F. & Newton, S. 2017 Stellarator bootstrap current and plasma flow velocity at low collisionality. J. Plasma Phys. 83 (2), 905830206.Google Scholar
Henneberg, S., Drevlak, M., Nührenberg, C., Beidler, C., Turkin, Y., Loizu, J. & Helander, P. 2019 Properties of a new quasi-axisymmetric configuration. Nucl. Fusion 59 (2), 026014.Google Scholar
Highcock, E., Mandell, N., Barnes, M. & Dorland, W. 2018 Optimisation of confinement in a fusion reactor using a nonlinear turbulence model. J. Plasma Phys. 84 (2), 905840208.Google Scholar
Hirshman, S., Shaing, K. & Van Rij, W. 1986a Consequences of time-reversal symmetry for the electric field scaling of transport in stellarators. Phys. Rev. Lett. 56 (16), 1697.Google Scholar
Hirshman, S. P., Shaing, K. C., van Rij, W. I., Beasley, C. O. & Crume, E. C. 1986b Plasma transport coefficients for nonsymmetric toroidal confinement systems. Phys. Fluids 29 (9), 2951–2959.Google Scholar
Hirshman, S., Spong, D., Whitson, J., Nelson, B., Batchelor, D., Lyon, J., Sanchez, R., Brooks, A., Y.-Fu, G., Goldston, R. et al. 1999 Physics of compact stellarators. Phys. Plasmas 6 (5), 1858–1864.Google Scholar
Hirshman, S. P. & Whitson, J. 1983 Steepest-descent moment method for three-dimensional magnetohydrodynamic equilibria. Phys. Fluids 26 (12), 3553–3568.Google Scholar
Kernbichler, W., Kasilov, S., Kapper, G., Martitsch, A. F., Nemov, V., Albert, C. & Heyn, M. 2016 Solution of drift kinetic equation in stellarators and tokamaks with broken symmetry using the code NEO-2. Plasma Phys. Control. Fusion 58 (10), 104001.Google Scholar
Krommes, J. A. & Hu, G. 1994 The role of dissipation in the theory and simulations of homogeneous plasma turbulence, and resolution of the entropy paradox. Phys. Plasmas 1 (10), 3211–3238.Google Scholar
Ku, L., Garabedian, P., Lyon, J., Turnbull, A., Grossman, A., Mau, T., Zarnstorff, M. & Team, A. 2008 Physics design for ARIES-CS. Fusion Sci. Technol. 54 (3), 673–693.Google Scholar
Landreman, M. & Paul, E. J. 2018 Computing local sensitivity and tolerances for stellarator physics properties using shape gradients. Nucl. Fusion 58 (7), 076023.Google Scholar
Landreman, M., Plunk, G. G. & Dorland, W. 2015 Generalized universal instability: transient linear amplification and subcritical turbulence. J. Plasma Phys. 81 (5), 905810501.Google Scholar
Landreman, M. & Sengupta, W. 2018 Direct construction of optimized stellarator shapes. Part 1. Theory in cylindrical coordinates. J. Plasma Phys. 84 (6), 905840616.Google Scholar
Landreman, M., Smith, H. M., Mollén, A. & Helander, P. 2014 Comparison of particle trajectories and collision operators for collisional transport in nonaxisymmetric plasmas. Phys. Plasmas 21 (4), 042503.Google Scholar
Lotz, W., Nührenberg, J. & Schwab, C. 1990 Optimization, MHD mode and alpha particle confinement behaviour of Helias equilibria. In Plasma Physics and Controlled Nuclear Fusion Research, vol. 2. International Atomic Energy Agency.Google Scholar
Maassberg, H., Lotz, W. & Nührenberg, J. 1993 Neoclassical bootstrap current and transport in optimized stellarator configurations. Phys. Fluids B 5 (10), 3728–3736.Google Scholar
Nelson, B., Berry, L., Brooks, A., Cole, M., Chrzanowski, J., Fan, H.-M., Fogarty, P., Goranson, P., Heitzenroeder, P., Hirshman, S. et al. 2003 Design of the National Compact Stellarator Experiment (NCSX). Fusion Engng Des. 66, 169–174.Google Scholar
Nemov, V., Kasilov, S., Kernbichler, W. & Heyn, M. 1999 Evaluation of 1/ $\unicode[STIX]{x1D708}$ neoclassical transport in stellarators. Phys. Plasmas 6 (12), 4622–4632.Google Scholar
Nocedal, J. & Wright, S. J. 1999 Numerical Optimization, chap. 6. Springer.Google Scholar
Nührenberg, J. & Zille, R. 1988 Quasi-helically symmetric toroidal stellarators. Phys. Lett. A 129, 113–117.Google Scholar
Paul, E. J., Landreman, M., Bader, A. & Dorland, W. 2018 An adjoint method for gradient-based optimization of stellarator coil shapes. Nucl. Fusion 58 (7), 076015.Google Scholar
Paul, E. J., Landreman, M., Poli, F. M., Spong, D. A., Smith, H. M. & Dorland, W. 2017 Rotation and neoclassical ripple transport in ITER. Nucl. Fusion 57 (11), 116044.Google Scholar
Pierce, N. A. & Giles, M. B. 2004 Adjoint and defect error bounding and correction for functional estimates. J. Comput. Phys. 200, 769–794.Google Scholar
Pironneau, O. 1974 On optimum design in fluid mechanics. J. Fluid Mech. 64 (1), 97–110.Google Scholar
Plessix, R.-E. 2006 A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophys. J. Intl 167 (2), 495–503.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 2007 Numerical Recipes 3rd Edition: The Art of Scientific Computing, chap. 9. Cambridge University Press.Google Scholar
Reiman, A., Fu, G., Hirshman, S., Ku, L., Monticello, D., Mynick, H., Redi, M., Spong, D., Zarnstorff, M., Blackwell, B. et al. 1999 Physics design of a high-quasi-axisymmetric stellarator. Plasma Phys. Control. Fusion 41 (12B), B273.Google Scholar
van Rij, W. I. & Hirshman, S. P. 1989 Variational bounds for transport coefficients in three-dimensional toroidal plasmas. Phys. Fluids B 1 (3), 563–569.Google Scholar
Rosenbluth, M., Hazeltine, R. & Hinton, F. L. 1972 Plasma transport in toroidal confinement systems. Phys. Fluids 15 (1), 116–140.Google Scholar
Rudin, W. 2006 Real and Complex Analysis, chap. 4. Tata McGraw-Hill Education.Google Scholar
Sanchez, R., Hirshman, S., Ware, A., Berry, L. & Spong, D. 2000 Ballooning stability optimization of low-aspect-ratio stellarators. Plasma Phys. Control. Fusion 42 (6), 641.Google Scholar
Sauer, T. 2012 Numerical Analysis, chap. 5. Pearson.Google Scholar
Shaing, K.-C., Crume, E. Jr, Tolliver, J., Hirshman, S. & Van Rij, W. 1989 Bootstrap current and parallel viscosity in the low collisionality regime in toroidal plasmas. Phys. Fluids B 1 (1), 148–152.Google Scholar
Spong, D., Hirshman, S., Whitson, J., Batchelor, D., Carreras, B., Lynch, V. & Rome, J. 1998 $J$ * optimization of small aspect ratio stellarator/tokamak hybrid devices. Phys. Plasmas 5 (5), 1752–1758.Google Scholar
Strickler, D. J., Hirshman, S. P., Spong, D. A., Cole, M. J., Lyon, J. F., Nelson, B. E., Williamson, D. E. & Ware, A. S. 2004 Development of a robust quasi-poloidal compact stellarator. Fusion Sci. Technol. 45 (1), 15–26.Google Scholar
Sugama, H., Watanabe, T.-H. & Nunami, M. 2009 Linearized model collision operators for multiple ion species plasmas and gyrokinetic entropy balance equations. Phys. Plasmas 16 (11), 112503.Google Scholar
Venditti, D. & Darmofal, D. 1999 A multilevel error estimation and grid adaptive strategy for improving the accuracy of integral outputs. In 14th Computational Fluid Dynamics Conference, p. 3292.Google Scholar
Zarnstorff, M., Berry, L., Brooks, A., Fredrickson, E., Fu, G., Hirshman, S., Hudson, S., Ku, L., Lazarus, E., Mikkelsen, D. et al. 2001 Physics of the compact advanced stellarator NCSX. Plasma Phys. Control. Fusion 43 (12A), A237.Google Scholar