Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T10:36:44.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Stellarator bootstrap current and plasma flow velocity at low collisionality

Part of: Focus on Fusion

Published online by Cambridge University Press:  23 March 2017

P. Helander ,
F. I. Parra  and
S. L. Newton
P. Helander*
Affiliation:
Max-Planck-Institut für Plasmaphysik, 17491 Greifswald, Germany
F. I. Parra
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Oxford OX1 3NP, UK Culham Centre for Fusion Energy, Culham Science Centre, Oxon OX14 3DB, UK
S. L. Newton
Affiliation:
Culham Centre for Fusion Energy, Culham Science Centre, Oxon OX14 3DB, UK Department of Physics, Chalmers University of Technology, 412 96 Göteborg, Sweden
*
†Email address for correspondence: per.helander@ipp.mpg.de
Get access Rights & Permissions [Opens in a new window]

Abstract

The bootstrap current and flow velocity of a low-collisionality stellarator plasma are calculated. As far as possible, the analysis is carried out in a uniform way across all low-collisionality regimes in general stellarator geometry, assuming only that the confinement is good enough that the plasma is approximately in local thermodynamic equilibrium. 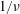It is found that conventional expressions for the ion flow speed and bootstrap current in the low-collisionality limit are accurate only in the $1/\unicode[STIX]{x1D708}$-collisionality regime and need to be modified in the 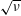$\sqrt{\unicode[STIX]{x1D708}}$-regime. The correction due to finite collisionality is also discussed and is found to scale as 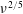$\unicode[STIX]{x1D708}^{2/5}$.

Keywords

fusion plasmaplasma confinementplasma flows
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 2 , April 2017 , 905830206
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beidler, C. D., Allmaier, K., Isaev, M. Y., Kasilov, S. V., Kernbichler, W., Leitold, G. O., Maassberg, H., Mikkelsen, D. R., Murakami, S., Schmidt, M. et al. 2011 Benchmarking of the mono-energetic transport coefficients-results from the International Collaboration on Neoclassical Transport in Stellarators (ICNTS). Nucl. Fusion 51 (7), 076001.Google Scholar
Beidler, C. D. & DHaeseleer, W. D. 1995 A general-solution of the ripple-averaged kinetic-equation (GSRAKE). Plasma Phys. Control. Fusion 37 (4), 463–490.Google Scholar
Boozer, A. H. 1983 Transport and isomorphic equilibria. Phys. Fluids 26 (2), 496–499.CrossRefGoogle Scholar
Braun, S. & Helander, P. 2010 Pfirsch–Schluter impurity transport in stellarators. Phys. Plasmas 17 (7), 072514.Google Scholar
Calvo, I., Parra, F. I., Alonso, J. A. & Velasco, J. L. 2014 Optimizing stellarators for large flows. Plasma Phys. Control. Fusion 56 (9), 094003; 19th International Stellarator-Heliotron Workshop held Jointly with the 16th Reversed Field Pinch Workshop, Padova, Italy, 16–20 September, 2013.CrossRefGoogle Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2013 Stellarators close to quasisymmetry. Plasma Phys. Control. Fusion 55 (12, 1–2), 125014.Google Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2015 Flow damping in stellarators close to quasisymmetry. Plasma Phys. Control. Fusion 57 (1), 014014.Google Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2017 The effect of tangential drifts on neoclassical transport in stellarators close to omnigeneity. Plasma Phys. Control. Fusion; accepted, arXiv:1610.06016 (2016).Google Scholar
Cary, J. R. & Shasharina, S. G. 1997 Omnigenity and quasihelicity in helical plasma confinement systems. Phys. Plasmas 4 (9), 3323–3333.Google Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77 (8), 087001.Google Scholar
Helander, P., Geiger, J. & Maassberg, H. 2011 On the bootstrap current in stellarators and tokamaks. Phys. Plasmas 18 (9), 092505.Google Scholar
Helander, P. & Nührenberg, J. 2009 Bootstrap current and neoclassical transport in quasi-isodynamic stellarators. Plasma Phys. Control. Fusion 51 (5), 055004.Google Scholar
Helander, P. & Sigmar, D. J. 2002 Collisional Transport in Magnetized Plasmas. Cambridge University Press.Google Scholar
Hinton, F. L. & Rosenbluth, M. N. 1973 Transport properties of a toroidal plasma at low-to-intermediate collision frequencies. Phys. Fluids 16 (6), 836–854.Google Scholar
Hirshman, S. P., Shaing, K. C., van Rij, W. I., Beasley, C. O. & Crume, E. C. 1986 Plasma transport-coefficients for nonsymmetric toroidal confinement systems. Phys. Fluids 29 (9), 2951–2959.Google Scholar
Hirshman, S. P. & Sigmar, D. J. 1981 Neoclassical transport of impurities in tokamak plasmas. Nucl. Fusion 21 (9), 1079–1201.Google Scholar
Ho, D. D. M. & Kulsrud, R. M. 1987 Neoclassical transport in stellarators. Phys. Fluids 30 (2), 442–461.CrossRefGoogle Scholar
Kernbichler, W., Kasilov, S. V., Kapper, K., Martitsch, A. V., Nemov, V. V., Albert, C. & Heyn, M. F. 2016 Solution of the drift kinetic equation in stellarators and tokamaks with broken symmetry using the code neo-2. Plasma Phys. Control. Fusion 56 (10), 104001.Google Scholar
Landreman, M. & Catto, P. J. 2011 Effects of the radial electric field in a quasisymmetric stellarator. Plasma Phys. Control. Fusion 53 (1), 015004.Google Scholar
Landreman, M. & Catto, P. J. 2012 Omnigenity as generalized quasisymmetry. Phys. Plasmas 19 (5), 056103.Google Scholar
Nakajima, N., Okamoto, M., Todoroki, J., Nakamura, Y. & Wakatani, M. 1989 Optimization of the bootstrap current in a large helical system with $L=2$ . Nucl. Fusion 29 (4), 605–616.Google Scholar
Parker, J. B. & Catto, P. J. 2012 Variational calculation of neoclassical ion heat flux and poloidal flow in the banana regime for axisymmetric magnetic geometry. Plasma Phys. Control. Fusion 54 (8), 085011.Google Scholar
Parra, F. I., Calvo, I., Helander, P. & Landreman, M. 2015 Less constrained omnigeneous stellarators. Nucl. Fusion 55 (3), 033005.Google Scholar
van Rij, W. I. & Hirshman, S. P. 1989 Variational bounds for transport-coefficients in 3-dimensional toroidal plasmas. Phys. Fluids B 1 (3), 563–569.Google Scholar
Rosenbluth, M. N., Hazeltine, R. D. & Hinton, F. L. 1972 Plasma transport in toroidal confinement systems. Phys. Fluids 15 (1), 116–140.Google Scholar
Shaing, K. C. & Callen, J. D. 1983 Neoclassical flows and transport in non-axisymmetric toroidal plasmas. Phys. Fluids 26 (11), 3315–3326.Google Scholar
Shaing, K. C., Carreras, B. A., Dominguez, N., Lynch, V. E. & Tolliver, J. S. 1989 Bootstrap current control in stellarators. Phys. Fluids B 1 (8), 1663–1670.Google Scholar
Simakov, A. N. & Helander, P. 2009 Neoclassical momentum transport in a collisional stellarator and a rippled tokamak. Phys. Plasmas 16 (4), 042503.Google Scholar
Taguchi, M. 1988 Ion thermal-conductivity and ion distribution function in the banana regime. Plasma Phys. Control. Fusion 30 (13), 1897–1904.Google Scholar
Weyl, H. 1916 Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77, 313–327.CrossRefGoogle Scholar