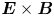1. Introduction
The control of radial particle transport in tokamak plasmas is a necessary, albeit not sufficient, condition for obtaining good confinement, and it is currently an area of intensive research (Hazeltine & Meiss Reference Hazeltine and Meiss2003; Horton & Benkadda Reference Horton and Benkadda2015). Such a goal can be achieved by creating internal transport barriers (ITBs), which are regions of reduced radial (cross-field) particle transport in the plasma column (Horton Reference Horton2018). Such ITBs have been produced in JET by the utilization of strong supplementary heating during the current rise phase of the plasma discharge (Wolf Reference Wolf2002).
Another type of transport barrier is the so-called edge transport barrier (ETB), related to steep pressure gradients at the plasma edge (Wolf Reference Wolf2002). These gradients arise due to the high pedestal pressure profiles, characteristic of H-mode confinement, and can also exist inside the plasma core (Goldston Reference Goldston1984; Yushmanov et al. Reference Yushmanov, Takizuka, Riedel, Kardaun, Cordey, Kaye and Post1990). This H-mode regime was obtained by combining neutral beam heating with a divertor configuration, showing a reduction of the particle and energy transport fluxes (Wagner et al. Reference Wagner, Becker, Behringer, Campbell, Eberhagen, Engelhardt, Fussmann, Gehre, Gernhardt and Gierke1982; Connor et al. Reference Connor, Fukuda, Garbet, Gormezano, Mukhovatov and Wakatani2004).
Recently, a second type of ITB has been investigated, the shearless transport barrier (STB), which appears in tokamak plasmas with reversed-shear profiles, and for which the pressure gradients do not need necessarily to be as large as for ETBs (Caldas et al. Reference Caldas, Viana, Abud, Fonseca, Guimarães Filho, Kroetz, Marcus, Schelin, Szezech and Toufen2012). Reversed-shear profiles can be obtained by modifying the safety factor profile (Connor et al. Reference Connor, Fukuda, Garbet, Gormezano, Mukhovatov and Wakatani2004), and by applying radial electric fields in a specific way (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). For example, reversed-shear profiles of $q(r)$![]() have one or more extrema, at which shearless toroidal magnetic surfaces are formed (Morrison Reference Morrison2000). Shearless surfaces represent ITBs in the sense that cross-field transport is reduced therein (Wolf Reference Wolf2002).
have one or more extrema, at which shearless toroidal magnetic surfaces are formed (Morrison Reference Morrison2000). Shearless surfaces represent ITBs in the sense that cross-field transport is reduced therein (Wolf Reference Wolf2002).
Another type of reversed shear appears by a suitable alteration of the tokamak equilibrium, which creates a non-monotonic radial electric field profile (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998; Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019). The presence of ITBs due to this effect can explain the reduction of turbulence-driven particle fluxes observed in tokamak experiments, leading to an improvement of the plasma confinement (Marcus et al. Reference Marcus, Caldas, Guimarães Filho, Morrison, Horton, Kuznetsov and Nascimento2008). Finally, ITBs have been related to reversed-shear profiles of the toroidal plasma velocity, measured in the Texas Helimak, where a set of probes is mounted to quantify velocity shear in different directions (Gentle et al. Reference Gentle, Liao, Lee and Rowan2010; Toufen et al. Reference Toufen, Guimarães Filho, Caldas, Marcus and Gentle2012).
The STBs are formed in mixed phase space with non-monotonic equilibrium profiles, containing regular particle trajectories as invariant curves and chaotic trajectories (del-Castillo-Negrete, Greene & Morrison Reference del-Castillo-Negrete, Greene and Morrison1996). Locally, the invariant curves separate the chaotic trajectories and prevent the global chaotic particle transport in phase space (del-Castillo-Negrete Reference del-Castillo-Negrete2000). Moreover, in STBs there are robust curves, namely shearless curves, which survive the increasing of the chaotic area and, consequently, are among the last invariant curves to be broken. This is a dynamical effect due to the perturbed trajectories in non-monotonic plasma profiles (del-Castillo-Negrete et al. Reference del-Castillo-Negrete, Greene and Morrison1996). The onset of STBs may be one of the mechanisms that hide behind certain improved scenarios observed in tokamaks with non-monotonic plasma profiles. In this work, we apply a model proposed by Horton et al. (Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998) to show how this mechanism depends on the required profiles.
The presence of different types of reversed shear (safety factor, radial electric field, toroidal plasma velocity) has been investigated by using a drift-wave test particle transport model (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). The latter is based on $\boldsymbol {E}\times \boldsymbol {B}$![]() drift combined with the advection of guiding-centre motion along the magnetic field lines (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). The numerical integration of guiding-centre trajectories leads to a Poincaré stroboscopic map, in which we sample the coordinates at integer multiples of some characteristic period (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1997). This kind of description, integrating particle trajectories, has led to important advances in the understanding of anomalous particle transport (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998; Kwon et al. Reference Kwon, Horton, Zhu, Morrison, Park and Choi2000; El Mouden et al. Reference El Mouden, Saifaoui, Zine and Eddahoy2007; Rosalem, Roberto & Caldas Reference Rosalem, Roberto and Caldas2014, Reference Rosalem, Roberto and Caldas2016; Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019), trapped particle transport (White & Chance Reference White and Chance1984) and generic magnetic perturbations (White Reference White2012).
drift combined with the advection of guiding-centre motion along the magnetic field lines (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). The numerical integration of guiding-centre trajectories leads to a Poincaré stroboscopic map, in which we sample the coordinates at integer multiples of some characteristic period (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1997). This kind of description, integrating particle trajectories, has led to important advances in the understanding of anomalous particle transport (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998; Kwon et al. Reference Kwon, Horton, Zhu, Morrison, Park and Choi2000; El Mouden et al. Reference El Mouden, Saifaoui, Zine and Eddahoy2007; Rosalem, Roberto & Caldas Reference Rosalem, Roberto and Caldas2014, Reference Rosalem, Roberto and Caldas2016; Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019), trapped particle transport (White & Chance Reference White and Chance1984) and generic magnetic perturbations (White Reference White2012).
The role of equilibrium profiles and oscillation spectrum in Horton's model has been studied previously. Rosalem et al. (Reference Rosalem, Roberto and Caldas2014) investigated the influence of the equilibrium electric field profiles on non-twist transport barriers and reported that monotonic profiles of electric field and safety factor do not generate a STB. Meanwhile, in the plasma edge, the trajectories are mainly determined by the plasma velocity profile (Rosalem et al. Reference Rosalem, Roberto and Caldas2016). The effect of the amplitude of oscillation has also been studied (El Mouden et al. Reference El Mouden, Saifaoui, Zine and Eddahoy2007; Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019; Osorio et al. Reference Osorio, Roberto, Caldas, Viana and Elskens2021). However, the influence of the safety factor profile has not yet been systematically investigated.
In this paper, we present a numerical investigation of the formation of single or multiple shearless curves due to reversed magnetic and electric shear profiles. The use of an $\boldsymbol {E}\times \boldsymbol {B}$![]() drift guiding-centre description allows us to choose the radial profiles for the safety factor, radial electric field and toroidal velocity. In this way, we are able to use reversed-shear profiles in order to study STBs. A numerically obtained Poincaré map is used to compute the rotation number profile, which takes into account all reversed-shear profiles. It turns out that there can be one or more STBs, corresponding to extrema of the rotation number profiles. Shearless curves can be created or destroyed by bifurcations triggered by suitably changing the safety factor profile. We also identify the dynamical mechanisms causing these shearless bifurcations.
drift guiding-centre description allows us to choose the radial profiles for the safety factor, radial electric field and toroidal velocity. In this way, we are able to use reversed-shear profiles in order to study STBs. A numerically obtained Poincaré map is used to compute the rotation number profile, which takes into account all reversed-shear profiles. It turns out that there can be one or more STBs, corresponding to extrema of the rotation number profiles. Shearless curves can be created or destroyed by bifurcations triggered by suitably changing the safety factor profile. We also identify the dynamical mechanisms causing these shearless bifurcations.
This paper is organized as follows. In § 2, we present the drift guiding-centre model to be used in the numerical simulations and the construction leading to the Poincaré map to be used in this work. Section 3 introduces the different reversed-shear profiles to be considered in the numerical simulations, showing the appearance of shearless surfaces at the extrema of rotation number profiles. In § 4, we discuss the possible shearless bifurcation scenarios. Our conclusions are left to the final section.
2. Drift-wave model
One of the characteristic features of anomalous cross-field transport in tokamak plasmas is the presence of electrostatic wave instabilities arising from density and temperature gradients (Horton & Benkadda Reference Horton and Benkadda2015). A wide spectrum of waves has been shown to produce radial transport fluxes of plasma particles (Horton Reference Horton2018). A mathematical model for describing the test particle motion in electrostatic waves has been proposed by Horton et al. (Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998), using a local coordinate system $\boldsymbol {x}=(r,\theta,\varphi )$![]() , where $r$
, where $r$![]() is the radius measured from the magnetic axis, with $\theta$
is the radius measured from the magnetic axis, with $\theta$![]() and $\varphi$
and $\varphi$![]() being the poloidal and toroidal angles, respectively. We denote by $a$
being the poloidal and toroidal angles, respectively. We denote by $a$![]() and $R$
and $R$![]() , respectively, the minor and major plasma radius.
, respectively, the minor and major plasma radius.
We consider the combined presence of an equilibrium magnetic field $\boldsymbol {B}$![]() and an electric field $\boldsymbol {E}$
and an electric field $\boldsymbol {E}$![]() related to the electrostatic waves. Moreover, let us suppose that the plasma particles are test particles, i.e. they are influenced by the external fields but do not affect them. In the applied model (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998), the $\boldsymbol {\nabla }{B}$
related to the electrostatic waves. Moreover, let us suppose that the plasma particles are test particles, i.e. they are influenced by the external fields but do not affect them. In the applied model (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998), the $\boldsymbol {\nabla }{B}$![]() and curvature drifts are neglected, and therefore trapped particle transport is not taken into account. Under these assumptions, the guiding-centre motion has two components: (a) a passive advection along the magnetic field lines, with velocity $v_\parallel$
and curvature drifts are neglected, and therefore trapped particle transport is not taken into account. Under these assumptions, the guiding-centre motion has two components: (a) a passive advection along the magnetic field lines, with velocity $v_\parallel$![]() , and (b) an $\boldsymbol {E}\times \boldsymbol {B}$
, and (b) an $\boldsymbol {E}\times \boldsymbol {B}$![]() drift velocity, so that the guiding-centre equation of motion is
drift velocity, so that the guiding-centre equation of motion is
In the large-aspect-ratio approximation ($\epsilon = a/R \ll 1$![]() ), we use a tokamak equilibrium magnetic field $\boldsymbol {B} = (0,B_\theta (r),B_\varphi )$
), we use a tokamak equilibrium magnetic field $\boldsymbol {B} = (0,B_\theta (r),B_\varphi )$![]() , where $B_\varphi$
, where $B_\varphi$![]() and $B_\theta$
and $B_\theta$![]() are the toroidal and poloidal magnetic field components, respectively. Since $B_\theta \sim \epsilon B_\varphi$
are the toroidal and poloidal magnetic field components, respectively. Since $B_\theta \sim \epsilon B_\varphi$![]() , we approximate $B \approx B_\varphi \gg B_\theta$
, we approximate $B \approx B_\varphi \gg B_\theta$![]() and treat $B$
and treat $B$![]() as a uniform field. The safety factor of the magnetic surfaces is thus given by
as a uniform field. The safety factor of the magnetic surfaces is thus given by
The model applied in this paper enables us to relate the advanced scenarios in tokamaks with the STBs predicted for the non-monotonic plasma profiles typical of these scenarios. To investigate this relation, it is assumed in this model (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998) that the electrostatic fluctuation spectrum is coherent and time-independent.
The assumed electric field can be expressed as $\boldsymbol {E} = {\bar {\boldsymbol {E}}_r(r)} - \boldsymbol {\nabla }{\tilde \phi }$![]() , where ${\bar {\boldsymbol {E}}_r}$
, where ${\bar {\boldsymbol {E}}_r}$![]() is a time-independent radial electric field profile and $\tilde {\boldsymbol {E}} = - \boldsymbol {\nabla } \tilde {\phi }$
is a time-independent radial electric field profile and $\tilde {\boldsymbol {E}} = - \boldsymbol {\nabla } \tilde {\phi }$![]() is a fluctuating part, representing the electrostatic instabilities in the tokamak edge (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). The latter is supposed to exhibit a broad spectrum of frequencies $\omega _n = n \omega _0$
is a fluctuating part, representing the electrostatic instabilities in the tokamak edge (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). The latter is supposed to exhibit a broad spectrum of frequencies $\omega _n = n \omega _0$![]() and wavevectors, characterized by the oscillation spectrum (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998):
and wavevectors, characterized by the oscillation spectrum (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998):
where $\alpha _{m,\ell,n}$![]() is the relative phase and $\phi _{m,\ell,n}$
is the relative phase and $\phi _{m,\ell,n}$![]() are constant coefficients. A radial-dependent spectrum was proposed by Connor & Taylor (Reference Connor and Taylor1987) and results in a global drift-wave map, valid for long times (Kwon et al. Reference Kwon, Horton, Zhu, Morrison, Park and Choi2000). However, to study local transport, we use the local drift-wave map, valid for short times (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). In this local map, we assume the coefficients $\phi _{m,\ell,n}$
are constant coefficients. A radial-dependent spectrum was proposed by Connor & Taylor (Reference Connor and Taylor1987) and results in a global drift-wave map, valid for long times (Kwon et al. Reference Kwon, Horton, Zhu, Morrison, Park and Choi2000). However, to study local transport, we use the local drift-wave map, valid for short times (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). In this local map, we assume the coefficients $\phi _{m,\ell,n}$![]() to be constants and consider only the dominant spatial mode in (2.3), with harmonics of the lowest angular frequency $\omega _0$
to be constants and consider only the dominant spatial mode in (2.3), with harmonics of the lowest angular frequency $\omega _0$![]() , and poloidal and toroidal mode numbers $m = M$
, and poloidal and toroidal mode numbers $m = M$![]() and $\ell = L$
and $\ell = L$![]() , respectively. Although the electrostatic fluctuations have a broad spectrum, the wavenumber width is smaller than the frequency width (Marcus et al. Reference Marcus, Caldas, Guimarães Filho, Morrison, Horton, Kuznetsov and Nascimento2008). Therefore, the numbers $M$
, respectively. Although the electrostatic fluctuations have a broad spectrum, the wavenumber width is smaller than the frequency width (Marcus et al. Reference Marcus, Caldas, Guimarães Filho, Morrison, Horton, Kuznetsov and Nascimento2008). Therefore, the numbers $M$![]() and $L$
and $L$![]() can be estimated by the highest amplitudes in the fluctuation spectrum. In this case, the electrostatic fluctuation spectrum becomes
can be estimated by the highest amplitudes in the fluctuation spectrum. In this case, the electrostatic fluctuation spectrum becomes
This model does not take into account the nonlinear interactions between the modes and the incoherent nature of the fluctuations. It supposes a single spatial mode of oscillation and a temporal spectrum concentrated in low frequencies. The correlation time and length of the fluctuation spectrum are key parameters for the validity of this theoretical analysis. If the correlation time $\tau _c$![]() is small compared with the circumnavigation time of the $\boldsymbol {E}\times \boldsymbol {B}$
is small compared with the circumnavigation time of the $\boldsymbol {E}\times \boldsymbol {B}$![]() motion $\tau _{\text {circ}}$
motion $\tau _{\text {circ}}$![]() , then the quasi-linear theory holds. However, if the perturbation has a correlation time long enough for a test particle to be able to feel the whole wave structure, we enter in trapping regime (Diamond, Itoh & Itoh Reference Diamond, Itoh and Itoh2010). The dimensionless Kubo number, defined by $K=\tau _c/\tau _{\text {circ}}$
, then the quasi-linear theory holds. However, if the perturbation has a correlation time long enough for a test particle to be able to feel the whole wave structure, we enter in trapping regime (Diamond, Itoh & Itoh Reference Diamond, Itoh and Itoh2010). The dimensionless Kubo number, defined by $K=\tau _c/\tau _{\text {circ}}$![]() , gives us a simple criterion: in the limit $K\ll 1$
, gives us a simple criterion: in the limit $K\ll 1$![]() the quasi-linear theory holds, and for $K>1$
the quasi-linear theory holds, and for $K>1$![]() the particle is in the trapping regime (Zimbardo, Pommois & Veltri Reference Zimbardo, Pommois and Veltri2000).
the particle is in the trapping regime (Zimbardo, Pommois & Veltri Reference Zimbardo, Pommois and Veltri2000).
Writing (2.1) in components, and taking into account the large-aspect-ratio approximation, yields
The guiding-centre equations of motion (2.5)–(2.7) are written in terms of the three radial profiles to be considered in this work. Defining action and angle variables (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998), $I=(r/a)^2$![]() and $\psi = M\theta - L\varphi$
and $\psi = M\theta - L\varphi$![]() , and performing a normalization (Appendix A), the set of three equations reduces to just two:
, and performing a normalization (Appendix A), the set of three equations reduces to just two:
The drift motion of the guiding centre of charged particles in combined magnetic and electric fields has been long known to be a Hamiltonian system, with canonical equations (Morrison Reference Morrison2000):
where the Hamiltonian can be written as $H(I,\psi,t) = H_0(I) + H_1(\psi,t)$![]() , where
, where
is the equilibrium part and
corresponds to the time-dependent perturbation. Hence, in general, the system is non-integrable.
If we switch off the perturbation caused by electrostatic fluctuation (this amounts to setting $\phi _n = 0$![]() for all values of $n$
for all values of $n$![]() ), (2.8) shows that the action variable is a constant of motion, as required from an integrable system (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1997). The perturbations of the quasi-integrable system (2.8)–(2.9) have resonant and non-resonant modes. The resonance condition for a perturbation mode $n$
), (2.8) shows that the action variable is a constant of motion, as required from an integrable system (Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1997). The perturbations of the quasi-integrable system (2.8)–(2.9) have resonant and non-resonant modes. The resonance condition for a perturbation mode $n$![]() is given by $({\rm d}/{\rm d} t) (\psi - n\omega _0 t) \approx 0$
is given by $({\rm d}/{\rm d} t) (\psi - n\omega _0 t) \approx 0$![]() , which implies
, which implies
Once the profiles of $q(I)$![]() , ${\bar {E}_r(I)}$
, ${\bar {E}_r(I)}$![]() and $v_\parallel (I)$
and $v_\parallel (I)$![]() are specified, it turns out that (2.13) is satisfied for a given $n$
are specified, it turns out that (2.13) is satisfied for a given $n$![]() only for certain values of the action $I = I_n$
only for certain values of the action $I = I_n$![]() . From Hamiltonian system theory, it follows that chains of periodic islands appear due to the perturbation, centred at those resonant values $I_n$
. From Hamiltonian system theory, it follows that chains of periodic islands appear due to the perturbation, centred at those resonant values $I_n$![]() .
.
In order to visualize those islands, we can use a Poincaré map obtained stroboscopically, i.e. we sample the values of the action–angle variables at integer multiples of a characteristic period, which is $\tau = 2{\rm \pi} /\omega _0$![]() in our system. Numerically integrating equations (2.8), we obtain stroboscopic Poincaré maps by plotting the trajectories in instants $t_j = j (2{\rm \pi} /\omega _0)$
in our system. Numerically integrating equations (2.8), we obtain stroboscopic Poincaré maps by plotting the trajectories in instants $t_j = j (2{\rm \pi} /\omega _0)$![]() . The two-dimensional map $I_{j+1} = I_{j+1}(I_j,\psi _j)$
. The two-dimensional map $I_{j+1} = I_{j+1}(I_j,\psi _j)$![]() , $\psi _{j+1} = \psi _{j+1}(I_j,\psi _j)$
, $\psi _{j+1} = \psi _{j+1}(I_j,\psi _j)$![]() is area-preserving because of the Liouville theorem (Hazeltine & Meiss Reference Hazeltine and Meiss2003).
is area-preserving because of the Liouville theorem (Hazeltine & Meiss Reference Hazeltine and Meiss2003).
Since we are interested chiefly in non-monotonic radial profiles corresponding to reversed-shear quantities like $q(I)$![]() , $v_\parallel (I)$
, $v_\parallel (I)$![]() and $E_r(I)$
and $E_r(I)$![]() , the Poincaré map is non-twist, i.e. the equilibrium Hamiltonian $H_0$
, the Poincaré map is non-twist, i.e. the equilibrium Hamiltonian $H_0$![]() has a point where
has a point where
Many results of the Hamiltonian theory, like Kolmogorov–Arnold–Moser theory and Aubry–Mather theory, hold only for twist systems, and hence new features are expected when non-twist maps are considered (del-Castillo-Negrete et al. Reference del-Castillo-Negrete, Greene and Morrison1996; Morrison Reference Morrison2000). One of them is the existence of twin island chains (del-Castillo-Negrete et al. Reference del-Castillo-Negrete, Greene and Morrison1996; Morrison Reference Morrison2000). These twin chains are centred at resonant values $I_n$![]() satisfying (2.13) that arise in pairs. The evolution of map orbits near twin chains has been extensively investigated for the so-called standard non-twist map (SNM).
satisfying (2.13) that arise in pairs. The evolution of map orbits near twin chains has been extensively investigated for the so-called standard non-twist map (SNM).
Introducing reversed-shear profiles in this model, transport barriers correspond to shearless invariant curves in phase space, defined by an extreme point in rotation number profile (del-Castillo-Negrete et al. Reference del-Castillo-Negrete, Greene and Morrison1996; Morrison Reference Morrison2000). To every regular (non-chaotic) orbit we can associate a rotation number $\varOmega$![]() given by the mean rotation angle in the Poincaré section. Given an initial condition $(I_0,\psi _0)$
given by the mean rotation angle in the Poincaré section. Given an initial condition $(I_0,\psi _0)$![]() , the rotation number of this orbit is given by
, the rotation number of this orbit is given by
where $\psi _N$![]() is the angle of the $N$
is the angle of the $N$![]() th intersection in the Poincaré map. We choose $\psi _0 = 0$
th intersection in the Poincaré map. We choose $\psi _0 = 0$![]() in numerical simulations, but the final value does not depend on that choice. The limit in (2.15) exists provided the orbit is non-chaotic.
in numerical simulations, but the final value does not depend on that choice. The limit in (2.15) exists provided the orbit is non-chaotic.
3. Breakup and reappearance of STBs
In this section, we show the presence of shearless invariant curves locally separating the chaotic trajectories and preventing plasma edge transport.
In order to numerically solve (2.8)–(2.9) we use parameters of TCABR (Nascimento et al. Reference Nascimento, Kuznetsov, Severo, Fonseca, Elfimov, Bellintani, Machida, Heller, Galvão and Sanada2005), although the results can be applied to any tokamak, described in a large-aspect-ratio approximation. However, we present a conceptual investigation rather than detailed comparisons with experiments performed in any tokamak.
The improvement of plasma confinement quality by using reversed-shear profiles has long been acknowledged. A substantial reduction of the turbulent transport levels has been observed in regions with negative magnetic shear (Mazzucato et al. Reference Mazzucato, Batha, Beer, Bell, Bell, Budny, Bush, Hahm, Hammett and Levinton1996; Connor et al. Reference Connor, Fukuda, Garbet, Gormezano, Mukhovatov and Wakatani2004). In order to generate negative shear regions, it is necessary that the safety factor radial profile be non-monotonic. Magnetohydrodynamics-based models of a cylindrical plasma column suggest the following profile of the safety factor (Kerner & Tasso Reference Kerner and Tasso1982):

where $q_a$![]() is the safety factor at the plasma edge and
is the safety factor at the plasma edge and
In the numerical simulations shown in this work, we fixed the parameters $\nu =0.8$![]() and $q_0=3.75$
and $q_0=3.75$![]() , making the remaining parameter $\mu$
, making the remaining parameter $\mu$![]() a function of $q_a$
a function of $q_a$![]() , which we choose as our control parameter. Such a high value of $q_0$
, which we choose as our control parameter. Such a high value of $q_0$![]() is not usual in common discharges but is present in strong reversed magnetic shear profiles for studies in ITER (Sips et al. Reference Sips2005; Joffrin Reference Joffrin2007). The $q(r)$
is not usual in common discharges but is present in strong reversed magnetic shear profiles for studies in ITER (Sips et al. Reference Sips2005; Joffrin Reference Joffrin2007). The $q(r)$![]() profile is plotted in figure 1(c) for some values of the control parameter. For $q_a = 3$
profile is plotted in figure 1(c) for some values of the control parameter. For $q_a = 3$![]() and $4$
and $4$![]() , the profile is non-monotonic, with minima at $r/a \approx 0.7$
, the profile is non-monotonic, with minima at $r/a \approx 0.7$![]() and $0.8$
and $0.8$![]() , respectively; whereas $q_a = 5$
, respectively; whereas $q_a = 5$![]() yields a quasi-monotonic profile, included here for completeness. This range of values of $q_a$
yields a quasi-monotonic profile, included here for completeness. This range of values of $q_a$![]() is compatible with TCABR plasma discharges (Nascimento et al. Reference Nascimento, Kuznetsov, Severo, Fonseca, Elfimov, Bellintani, Machida, Heller, Galvão and Sanada2005).
is compatible with TCABR plasma discharges (Nascimento et al. Reference Nascimento, Kuznetsov, Severo, Fonseca, Elfimov, Bellintani, Machida, Heller, Galvão and Sanada2005).

Figure 1. Profiles of (a) radial electric field, (b) parallel velocity, (c) non-monotonic safety factor profile and (d) resonant mode numbers as a function of the action value for different values of $q_a$![]() . Since only integer values of $n$
. Since only integer values of $n$![]() are allowed, it follows that only the modes $n = 3$
are allowed, it follows that only the modes $n = 3$![]() and $4$
and $4$![]() produce resonances.
produce resonances.
The presence of negative shear in the radial electric field profile has been related to the reduction of turbulent particle fluxes in H-mode tokamak discharges (Viezzer et al. Reference Viezzer, Pütterich, Conway, Dux, Happel, Fuchs, McDermott, Ryter, Sieglin and Suttrop2013). This effect is compatible with a STB if the radial profile of $E_r$![]() is non-monotonic (Marcus et al. Reference Marcus, Caldas, Guimarães Filho, Morrison, Horton, Kuznetsov and Nascimento2008, Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019). One of the simplest functions with this property is a quadratic one, given by
is non-monotonic (Marcus et al. Reference Marcus, Caldas, Guimarães Filho, Morrison, Horton, Kuznetsov and Nascimento2008, Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019). One of the simplest functions with this property is a quadratic one, given by
where $\alpha = -1.14$![]() , $\beta = 2.529$
, $\beta = 2.529$![]() and $\gamma = -2.639$
and $\gamma = -2.639$![]() are parameter values after normalization (see Appendix A for details). These values were chosen to yield a local minimum in the desired plasma region and are compatible with profiles measured in the TCABR tokamak (Nascimento et al. Reference Nascimento, Kuznetsov, Severo, Fonseca, Elfimov, Bellintani, Machida, Heller, Galvão and Sanada2005).
are parameter values after normalization (see Appendix A for details). These values were chosen to yield a local minimum in the desired plasma region and are compatible with profiles measured in the TCABR tokamak (Nascimento et al. Reference Nascimento, Kuznetsov, Severo, Fonseca, Elfimov, Bellintani, Machida, Heller, Galvão and Sanada2005).
Toroidal plasma rotation is an important effect to be taken into account in tokamaks, such as stabilization or growth rate decrease of certain magnetohydrodynamic modes. Besides intrinsic rotation, this effect can also be obtained by using neutral beam injection, since the incident particles impart momentum to the plasma particles. Moreover, it has been observed that plasma rotation is able to decrease turbulent flux levels in the plasma edge (Gentle et al. Reference Gentle, Liao, Lee and Rowan2010; Toufen et al. Reference Toufen, Guimarães Filho, Caldas, Marcus and Gentle2012). Hence, it has been conjectured that non-monotonic profiles of the toroidal plasma velocity can be related to ITBs (actually, shearless barriers).
Spectroscopic techniques have been used for the measurement of toroidal plasma rotation velocities in TCABR discharges, giving values of about $3.0\,{\rm km}\,{\rm s}^{-1}$![]() for the plasma edge (Nascimento et al. Reference Nascimento, Kuznetsov, Severo, Fonseca, Elfimov, Bellintani, Machida, Heller, Galvão and Sanada2005). A normalized parallel velocity profile used in this work, and consistent with TCABR observations, is given by
for the plasma edge (Nascimento et al. Reference Nascimento, Kuznetsov, Severo, Fonseca, Elfimov, Bellintani, Machida, Heller, Galvão and Sanada2005). A normalized parallel velocity profile used in this work, and consistent with TCABR observations, is given by
where the parameters take the following values: $v_{\parallel 0} =-3.15$![]() , $v_m=5.58$
, $v_m=5.58$![]() , $\sigma _1 = 14.1$
, $\sigma _1 = 14.1$![]() and $\sigma _2 = -9.26$
and $\sigma _2 = -9.26$![]() , once we apply the normalization factor $v_0=E_0/B_0$
, once we apply the normalization factor $v_0=E_0/B_0$![]() (Osorio et al. Reference Osorio, Roberto, Caldas, Viana and Elskens2021). Profiles of $E_r$
(Osorio et al. Reference Osorio, Roberto, Caldas, Viana and Elskens2021). Profiles of $E_r$![]() and $v_{\|}$
and $v_{\|}$![]() are shown in figure 1(a,b).
are shown in figure 1(a,b).
After discussing the equilibrium aspects of the model, let us consider the perturbation caused by the electrostatic fluctuations given by (2.4). We assume the spatial dominant mode to have $M/L=16/4$![]() , which are typical numbers in the wave spectrum at the tokamak plasma edge (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). The temporal modes considered are $n=2,3,4$
, which are typical numbers in the wave spectrum at the tokamak plasma edge (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998). The temporal modes considered are $n=2,3,4$![]() , based on the fluctuating spectrum of TCABR (Marcus et al. Reference Marcus, Caldas, Guimarães Filho, Morrison, Horton, Kuznetsov and Nascimento2008), with normalized amplitudes $\phi _2=11.74 \times 10^{-3}$
, based on the fluctuating spectrum of TCABR (Marcus et al. Reference Marcus, Caldas, Guimarães Filho, Morrison, Horton, Kuznetsov and Nascimento2008), with normalized amplitudes $\phi _2=11.74 \times 10^{-3}$![]() , $\phi _3=2.077 \times 10^{-3}$
, $\phi _3=2.077 \times 10^{-3}$![]() and $\phi _4=0.2443 \times 10^{-3}$
and $\phi _4=0.2443 \times 10^{-3}$![]() . The fundamental frequency of the temporal modes is around $10\,\mathrm {kHz}$
. The fundamental frequency of the temporal modes is around $10\,\mathrm {kHz}$![]() (Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019), which implies a normalized angular frequency $\omega _0=5.224$
(Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019), which implies a normalized angular frequency $\omega _0=5.224$![]() . We keep $\alpha _n=0$
. We keep $\alpha _n=0$![]() and the perturbation amplitudes at these values throughout this work.
and the perturbation amplitudes at these values throughout this work.
Assuming that the rest of the profiles and parameters are fixed, the safety factor is chosen to be the tunable parameter which determines the dynamical behaviour of the system. Given a $q_a$![]() value, as mentioned before, there are resonant actions $I_n$
value, as mentioned before, there are resonant actions $I_n$![]() determined by the condition (2.13), whose numerical solution is shown in figure 1(d) for different values of $q_a$
determined by the condition (2.13), whose numerical solution is shown in figure 1(d) for different values of $q_a$![]() . The mode $n=3$
. The mode $n=3$![]() produces a resonance at two values of the action $I_{3,(a,b)}$
produces a resonance at two values of the action $I_{3,(a,b)}$![]() , which also characterizes non-twist behaviour. The $n=4$
, which also characterizes non-twist behaviour. The $n=4$![]() mode, however, gives a resonance at a single value $I_4$
mode, however, gives a resonance at a single value $I_4$![]() . In addition, the $n=2$
. In addition, the $n=2$![]() mode does not yield resonance at any value of $I$
mode does not yield resonance at any value of $I$![]() , but it nevertheless influences the formation and destruction of STBs (Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019).
, but it nevertheless influences the formation and destruction of STBs (Marcus et al. Reference Marcus, Roberto, Caldas, Rosalem and Elskens2019).
The variation of the safety factor profile changes the behaviour of STBs. Figure 2 displays examples of Poincaré sections for some values of control parameter $q_a$![]() . We represent the action–angle variables as rectangular coordinates for better visualization. In figure 2(a), obtained for $q_a = 5.00$
. We represent the action–angle variables as rectangular coordinates for better visualization. In figure 2(a), obtained for $q_a = 5.00$![]() , we observe two large (twin) islands and a chaotic region around the inner one (the outer island has also a chaotic region, but it is too narrow to be seen with the present resolution).
, we observe two large (twin) islands and a chaotic region around the inner one (the outer island has also a chaotic region, but it is too narrow to be seen with the present resolution).

Figure 2. Poincaré sections in the action–angle variables obtained by numerical integration of the equations of drift motion, for different values of the safety factor at plasma edge: (a) $q_a = 5.00$![]() , (b) $q_a = 4.50$
, (b) $q_a = 4.50$![]() , (c) $q_a = 4.00$
, (c) $q_a = 4.00$![]() , (d) $q_a = 3.45$
, (d) $q_a = 3.45$![]() , (e) $q_a = 3.30$
, (e) $q_a = 3.30$![]() and (f) $q_a = 3.00$
and (f) $q_a = 3.00$![]() . The shearless curves are indicated by green, red and blue wherever they appear in the Poincaré sections.
. The shearless curves are indicated by green, red and blue wherever they appear in the Poincaré sections.
Those islands refer to the main resonances of $n=3$![]() mode in figure 1 and are direct consequences of the non-monotonicity of the profiles. Between these twin islands, there is a shearless curve, located at the action value corresponding to an extremum of the rotation number profile (figure 3a). There are other island chains corresponding to higher-order resonances, but their width is considerably smaller than the main ones, and their effect will not be taken into account, at least not directly.
mode in figure 1 and are direct consequences of the non-monotonicity of the profiles. Between these twin islands, there is a shearless curve, located at the action value corresponding to an extremum of the rotation number profile (figure 3a). There are other island chains corresponding to higher-order resonances, but their width is considerably smaller than the main ones, and their effect will not be taken into account, at least not directly.
The chaotic region around the inner islands grows as the parameter $q_a$![]() decreases and eventually causes the breakup of the shearless curve for $q_a = 4.50$
decreases and eventually causes the breakup of the shearless curve for $q_a = 4.50$![]() (figure 2b). The mechanism of shearless curve breakup due to increasing perturbation has been thoroughly described by Morrison and co-workers, in the context of the SNM, introduced by del-Castillo-Negrete et al. (Reference del-Castillo-Negrete, Greene and Morrison1996):
(figure 2b). The mechanism of shearless curve breakup due to increasing perturbation has been thoroughly described by Morrison and co-workers, in the context of the SNM, introduced by del-Castillo-Negrete et al. (Reference del-Castillo-Negrete, Greene and Morrison1996):
where $(I_n,\theta _n)$![]() can be regarded as action–angle variables of the drift model when we consider a quadratic approximation of the radial safety factor profile about a local extremum (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998), and ${\tilde a}$
can be regarded as action–angle variables of the drift model when we consider a quadratic approximation of the radial safety factor profile about a local extremum (Horton et al. Reference Horton, Park, Kwon, Strozzi, Morrison and Choi1998), and ${\tilde a}$![]() , ${\tilde b}$
, ${\tilde b}$![]() are system parameters. In this work, we vary the equilibrium magnetic field configuration while keeping constant the perturbation amplitude. Furthermore, we find new scenarios for the shearless curve onset and breakup. Moreover, a map (discrete-time) model can be obtained if we consider a wide frequency spectrum of equally spaced resonant modes, instead of a single dominant resonant mode.
are system parameters. In this work, we vary the equilibrium magnetic field configuration while keeping constant the perturbation amplitude. Furthermore, we find new scenarios for the shearless curve onset and breakup. Moreover, a map (discrete-time) model can be obtained if we consider a wide frequency spectrum of equally spaced resonant modes, instead of a single dominant resonant mode.
Of note, if the value of $q_a$![]() is further decreased to $4.00$
is further decreased to $4.00$![]() , the shearless curve between the two twin islands reappears (figure 2c), since the corresponding rotation number profile has an extremum for this parameter value. This new shearless curve, on its way, is broken for smaller values of $q_a$
, the shearless curve between the two twin islands reappears (figure 2c), since the corresponding rotation number profile has an extremum for this parameter value. This new shearless curve, on its way, is broken for smaller values of $q_a$![]() , like $3.45$
, like $3.45$![]() (figure 2d).
(figure 2d).
Further decrease in $q_a$![]() causes the appearance of three shearless curves at $q_a = 3.30$
causes the appearance of three shearless curves at $q_a = 3.30$![]() (plotted in red, green and blue in figure 2e). They are also located at extrema of the rotation number profile: the red one at a maximum, and the green and blue ones at minima (figure 3b). These multiple shearless curves also disappear for even lower values of $q_a$
(plotted in red, green and blue in figure 2e). They are also located at extrema of the rotation number profile: the red one at a maximum, and the green and blue ones at minima (figure 3b). These multiple shearless curves also disappear for even lower values of $q_a$![]() , as exemplified by figure 2(f), obtained for $q_a = 3.00$
, as exemplified by figure 2(f), obtained for $q_a = 3.00$![]() . In this Poincaré map, we can see that even after the shearless curve breakup a partial transport barrier persists, as seen by the density of points, due to the stickiness effect.
. In this Poincaré map, we can see that even after the shearless curve breakup a partial transport barrier persists, as seen by the density of points, due to the stickiness effect.
The stickiness phenomenon occurs when a chaotic orbit in the vicinity of periodic island chains spends a large amount of time encircling it, after which it is free to diffuse until it approaches the neighbourhood of another periodic orbit, where it may be trapped again, and so on. This results in an anomalous diffusion scenario, whereby the orbit experiences long periods of trapping, interspersed by fast diffusion in the chaotic sea. This trapping near a periodic island is attributed to the existence of cantori, or tori perforated in a self-similar way, and the stickiness-induced trapping can be quantified by the calculation of the finite-time Lyapunov exponents (Szezech et al. Reference Szezech, Caldas, Lopes, Viana and Morrison2009). The mechanism for orbit escape through cantori involves a structure called turnstiles, formed by segments of invariant manifolds of unstable periodic orbits embedded in the chaotic sea (MacKay, Meiss & Percival Reference MacKay, Meiss and Percival1984).
A related investigation, reported in Szezech et al. (Reference Szezech, Caldas, Lopes, Morrison and Viana2012), quantifies the transport properties of the SNM, due to the STB, using a novel concept, the finite-time rotation number, which is computed in the same way as the conventional rotation number, but using a short period of time. The statistical properties of the finite-time rotation number are remarkably similar to those of the finite-time Lyapunov exponents. For example, Lagrangian coherent structures (LCS) can be obtained by considering the ridges of the scalar field of the finite-time rotation number, over a given phase space region. The LCS are structures that have properties similar to those of the invariant manifolds of periodic orbits but, unlike the latter, are defined in more general contexts (e.g. when there is explicit time dependence), which allows their use in a wide variety of plasma physics applications (Falessi, Pegoraro & Schep Reference Falessi, Pegoraro and Schep2015). In addition, LCS can also be interpreted as transport barriers, and their description reveals escape patterns for the $\boldsymbol {E}\times \boldsymbol {B}$![]() motion of plasma particles.
motion of plasma particles.
Sequences of breakup and reappearance of shearless curves as a parameter is varied, exemplified by figure 2(a–c), occur quite often in the non-twist system considered in this work. In figure 4 we plot a shearless bifurcation diagram, showing the extrema of rotation number as a function of the parameter $q_a$![]() . Hence, each point in this diagram corresponds to a shearless curve, whenever it exists. There are some gaps in the diagram, corresponding to parameter values with no extrema of $\varOmega$
. Hence, each point in this diagram corresponds to a shearless curve, whenever it exists. There are some gaps in the diagram, corresponding to parameter values with no extrema of $\varOmega$![]() , or for which the rotation number itself is ill-defined (because the considered orbit is chaotic, for example). Such regions are indicated in black in the bar at the top of figure 4.
, or for which the rotation number itself is ill-defined (because the considered orbit is chaotic, for example). Such regions are indicated in black in the bar at the top of figure 4.

Figure 4. Shearless bifurcation diagram showing the extrema of the rotation number profile (whenever they exist) as a function of the control parameter $q_a$![]() . Blue and green points indicate the observation of two and three extrema, respectively. In the top colour bar, black regions represent intervals for which there is no shearless curve.
. Blue and green points indicate the observation of two and three extrema, respectively. In the top colour bar, black regions represent intervals for which there is no shearless curve.
For most parameter values in the shearless bifurcation diagram, there is only one shearless curve, represented by red points in figure 4, corresponding to the red regions in the colour bar. Multiple shearless curves are indicated by blue and green points, when there are two and three coexisting shearless curves, respectively. In the inset of figure 4 we display a magnification of the interval $3.1< q_a<3.4$![]() , for which there are green points indicating three coexisting shearless curves. There are some blue points as well, but they occupy a region so small that they are barely visible in figure 4.
, for which there are green points indicating three coexisting shearless curves. There are some blue points as well, but they occupy a region so small that they are barely visible in figure 4.
We see that a shearless bifurcation is an abrupt change in the behaviour of the shearless curve as a system parameter is varied through a critical value. For example, a change between red and green points in figure 4 suggests the occurrence of a shearless bifurcation, whereby a single shearless curve bifurcates into two shearless curves as the parameter $q_a$![]() passes through some value. When green points become red points again, we can speak of an inverse shearless bifurcation. Bifurcations on transport barriers like the one mentioned above were experimentally observed for JET and ASDEX Upgrade (Joffrin et al. Reference Joffrin, Challis, Conway, Garbet, Gude, Günter, Hawkes, Hender, Howell and Huysmans2003). However, in these experiments, the triggering mechanism of those barriers is different from the one presented in this paper, but the possibility of having more than one transport barrier remains.
passes through some value. When green points become red points again, we can speak of an inverse shearless bifurcation. Bifurcations on transport barriers like the one mentioned above were experimentally observed for JET and ASDEX Upgrade (Joffrin et al. Reference Joffrin, Challis, Conway, Garbet, Gude, Günter, Hawkes, Hender, Howell and Huysmans2003). However, in these experiments, the triggering mechanism of those barriers is different from the one presented in this paper, but the possibility of having more than one transport barrier remains.
4. Shearless bifurcation scenarios
The shearless curves undergo bifurcations of many types. In the most frequent, the shearless curve simply disappears as a control parameter passes through some critical value. Since shearless curves represent transport barriers, their breakup will be followed by a significant increase in the transport levels (Szezech et al. Reference Szezech, Caldas, Lopes, Viana and Morrison2009). After the breakup of a shearless curve, a larger chaotic region would enable the guiding centres to undergo longer excursions in action space (Szezech et al. Reference Szezech, Caldas, Lopes, Viana and Morrison2009). However, if limited regions of chaotic orbits exist before the shearless curve breaks down, the curve breakup is not expected to increase significantly the transport levels.
In the SNM, after the shearless curve disappears, global chaotic transport appears in phase space, since at both sides of the shearless curve there are locally chaotic regions that merge together after the curve breakup, leaving a larger chaotic region therein. We observed that the system (2.8)–(2.9) manifests some atypical shearless breakups. Two of them are shown in figures 5 and 6. Each one depicts a shearless breakup in one of the reconnection scenarios of the SNM.

Figure 5. Poincaré sections of the drift-wave model for (a) $q_a=3.1290$![]() , (b) magnification of marked region in (a), (c) $q_a=3.1282$
, (b) magnification of marked region in (a), (c) $q_a=3.1282$![]() , (d) $q_a=3.1277$
, (d) $q_a=3.1277$![]() and (e) $q_a=3.1272$
and (e) $q_a=3.1272$![]() . The remaining parameter values are the same as in figure 2. In these phase portraits, we magnify the region containing the twin islands of $19$
. The remaining parameter values are the same as in figure 2. In these phase portraits, we magnify the region containing the twin islands of $19$![]() islands each, straddling the shearless curve.
islands each, straddling the shearless curve.

Figure 6. Poincaré sections of the drift-wave model for (a) $q_a=3.700$![]() , (b) $q_a=3.725$
, (b) $q_a=3.725$![]() , (c) $q_a=3.730$
, (c) $q_a=3.730$![]() and (d) $q_a=3.740$
and (d) $q_a=3.740$![]() . The remaining parameter values are the same as in figure 2.
. The remaining parameter values are the same as in figure 2.
Figure 5 shows an odd reconnection scenario involving the shearless curve. Figure 5(a) displays the shearless curve (in red) located between twin chains of $19$![]() islands each (in cyan and magenta), evident in the magnification of the rectangle area (figure 5b). A slight decrease in the value of the control parameter $q_a$
islands each (in cyan and magenta), evident in the magnification of the rectangle area (figure 5b). A slight decrease in the value of the control parameter $q_a$![]() leads to a collision of both island chains with the shearless curve and, in this process, the STB breaks up (figure 5c). A further decrease in $q_a$
leads to a collision of both island chains with the shearless curve and, in this process, the STB breaks up (figure 5c). A further decrease in $q_a$![]() causes the reappearance of a shearless curve in a meandering form, separating the two island chains (figure 5d). Lowering further the parameter $q_a$
causes the reappearance of a shearless curve in a meandering form, separating the two island chains (figure 5d). Lowering further the parameter $q_a$![]() , this odd reconnection scenario involves the extinction of the twin islands, leaving only the meandering invariant curves, separated by the surviving shearless curve (figure 5e).
, this odd reconnection scenario involves the extinction of the twin islands, leaving only the meandering invariant curves, separated by the surviving shearless curve (figure 5e).
A sequence of Poincaré sections showing an even reconnection scenario is depicted in figure 6. For a given value of $q_a$![]() there are twin chains of four islands each (marked green and blue), straddling a shearless curve (in red) (a magnification of the phase portrait, showing only two islands in each chain, is displayed in figure 6a). For the current value of the amplitudes considered in this figure, there are already two sizeable chaotic regions on both sides of the shearless curve, where the remnants of the islands are embedded.
there are twin chains of four islands each (marked green and blue), straddling a shearless curve (in red) (a magnification of the phase portrait, showing only two islands in each chain, is displayed in figure 6a). For the current value of the amplitudes considered in this figure, there are already two sizeable chaotic regions on both sides of the shearless curve, where the remnants of the islands are embedded.
As the control parameter $q_a$![]() slightly increases, the twin island chains approach each other and reconnect, causing a transition when the shearless curve is absent (figure 6b), although the STB is still present. Increasing again $q_a$
slightly increases, the twin island chains approach each other and reconnect, causing a transition when the shearless curve is absent (figure 6b), although the STB is still present. Increasing again $q_a$![]() , the lower island chain (green) disappears, leaving only the upper chain (blue), showing an asymmetry characteristic of this even reconnection scenario (figure 6c). After this remaining island disappears, for increasing $q_a$
, the lower island chain (green) disappears, leaving only the upper chain (blue), showing an asymmetry characteristic of this even reconnection scenario (figure 6c). After this remaining island disappears, for increasing $q_a$![]() , the shearless curve reappears (figure 6d). The asymmetric behaviour of this even reconnection scenario is a characteristic of non-twist maps with a lack of symmetry, such as the considered model. For example, the SNM (3.5) has symmetry with respect to action coordinate (del-Castillo-Negrete et al. Reference del-Castillo-Negrete, Greene and Morrison1996). However, most other maps do not have such property, like the extended SNM (Wurm & Martini Reference Wurm and Martini2013).
, the shearless curve reappears (figure 6d). The asymmetric behaviour of this even reconnection scenario is a characteristic of non-twist maps with a lack of symmetry, such as the considered model. For example, the SNM (3.5) has symmetry with respect to action coordinate (del-Castillo-Negrete et al. Reference del-Castillo-Negrete, Greene and Morrison1996). However, most other maps do not have such property, like the extended SNM (Wurm & Martini Reference Wurm and Martini2013).
Another category of shearless bifurcations concerns the appearance of more than one shearless curve, as illustrated by figure 7. For $q_a = 3.2360$![]() there are four island chains, two of them at each side of a shearless curve, marked in magenta, blue, green and cyan. As in the previous figure, the amplitude of the perturbation is already large enough to create two large chaotic regions at each side of the shearless curve, which acts as a transport barrier, in this case preventing large-scale excursion of particles in chaotic orbits.
there are four island chains, two of them at each side of a shearless curve, marked in magenta, blue, green and cyan. As in the previous figure, the amplitude of the perturbation is already large enough to create two large chaotic regions at each side of the shearless curve, which acts as a transport barrier, in this case preventing large-scale excursion of particles in chaotic orbits.

Figure 7. Poincaré sections of the drift-wave model for (a) $q_a=3.2360$![]() , (b) magnification of a region of (a), (c) $q_a=3.23841$
, (b) magnification of a region of (a), (c) $q_a=3.23841$![]() , (d) magnification of a region of (c) and (e) $q_a=3.23849$
, (d) magnification of a region of (c) and (e) $q_a=3.23849$![]() . (f) A zoom out of (e). The remaining parameter values are the same as in figure 2. This sequence represents a scenario containing four isochronous chains (magenta, cyan, blue and green) originating shearless bifurcations. The periodic points of the magenta chain, in (a,b), collide in a saddle–centre bifurcation (c) and a second shearless curve arises in (d) after the suppression of pink and gold twin island chains, containing 73 islands each (e).
. (f) A zoom out of (e). The remaining parameter values are the same as in figure 2. This sequence represents a scenario containing four isochronous chains (magenta, cyan, blue and green) originating shearless bifurcations. The periodic points of the magenta chain, in (a,b), collide in a saddle–centre bifurcation (c) and a second shearless curve arises in (d) after the suppression of pink and gold twin island chains, containing 73 islands each (e).
Let us consider the vicinity of one island of the magenta chain in more detail, as revealed by the magnification shown in figure 7(b). On changing the control parameter value, the periodic points of the chain collide and a chaotic layer takes their place, containing a myriad of islands (figure 7c). This collision represents a saddle–centre bifurcation: we have pairs of periodic points, half of them locally stable (centres) and the other half unstable (saddles). As the control parameter increases, these pairs of periodic points approach each other and eventually coalesce at the bifurcation points, disappearing afterwards, and leaving a chaotic layer therein. In this myriad of islands there is a pair of twin island chains, with 73 islands each marked in gold and pink, having the same rotation number (figure 7d). A bifurcation process extinguishes those twin island chains and generates a second shearless curve, plotted in blue in figure 7(e). Finally, figure 7(f) displays the full scenario with the two shearless curves. We remark that the appearance of the second shearless curve is a bifurcation in the rotation number profile, whereas the saddle–centre (O–X) bifurcation which precedes the latter occurs in phase space (here represented by Poincaré sections). Bifurcations of this type have been observed in some atypical scenarios in the SNM (Wurm et al. Reference Wurm, Apte, Fuchss and Morrison2005).
The process detailed in figure 8 is analogous to figure 7 and leads to a third shearless curve, through the same kind of shearless bifurcation. In figure 8(a), obtained for $q_a = 3.2451$![]() , we show a scenario just after the appearance of a second shearless curve, straddling two chaotic regions. In this Poincaré section, below the shearless curve, there is a chain of five tiny islands, one of which is magnified and shown in cyan in figure 8(b). Starting from this island (as well as the other ones in the same chain), a third shearless curve emerges, which is plotted in green in figure 8(c). In this example, another saddle–centre bifurcation occurs in the Poincaré section, leading to secondary twin island chains with 58 islands each (not shown in the figure), which precedes the shearless bifurcation causing the emergence of the third shearless curve. The scenario after the emergence of the green shearless curve is depicted in figure 2(e).
, we show a scenario just after the appearance of a second shearless curve, straddling two chaotic regions. In this Poincaré section, below the shearless curve, there is a chain of five tiny islands, one of which is magnified and shown in cyan in figure 8(b). Starting from this island (as well as the other ones in the same chain), a third shearless curve emerges, which is plotted in green in figure 8(c). In this example, another saddle–centre bifurcation occurs in the Poincaré section, leading to secondary twin island chains with 58 islands each (not shown in the figure), which precedes the shearless bifurcation causing the emergence of the third shearless curve. The scenario after the emergence of the green shearless curve is depicted in figure 2(e).

Figure 8. Poincaré sections of the drift-wave model for (a) $q_a=3.2451$![]() , (b) magnification of a region of (a) and (c) $q_a=3.2527$
, (b) magnification of a region of (a) and (c) $q_a=3.2527$![]() . The remaining parameter values are the same as in figure 2. This scenario illustrates the emergence of a third shearless curve through a saddle-node bifurcation.
. The remaining parameter values are the same as in figure 2. This scenario illustrates the emergence of a third shearless curve through a saddle-node bifurcation.
The last scenario of shearless bifurcation presented in this paper is shown in figure 9. For $q_a=3.365$![]() we see, in the Poincaré section, three shearless curves, marked in blue, red and green (figure 9a). The rotation number profile corresponding to this case (figure 9c) has three extrema: one maximum, corresponding to the red shearless curve, and two minima, corresponding to the green and blue curves. As the control parameter increases slightly, the red and blue shearless curves collide at a critical value of $q_a$
we see, in the Poincaré section, three shearless curves, marked in blue, red and green (figure 9a). The rotation number profile corresponding to this case (figure 9c) has three extrema: one maximum, corresponding to the red shearless curve, and two minima, corresponding to the green and blue curves. As the control parameter increases slightly, the red and blue shearless curves collide at a critical value of $q_a$![]() . After the collision, these shearless curves mutually annihilate, leaving only the green shearless curve (figure 9b), as confirmed by the rotation number profile for this value of $q_a$
. After the collision, these shearless curves mutually annihilate, leaving only the green shearless curve (figure 9b), as confirmed by the rotation number profile for this value of $q_a$![]() (figure 9d), which exhibits only the minimum corresponding to the green shearless curve.
(figure 9d), which exhibits only the minimum corresponding to the green shearless curve.

Figure 9. Poincaré sections of the drift-wave model: (a) magnification of a region when $q_a=3.365$![]() ; (b) magnification of a region when $q_a = 3.367$
; (b) magnification of a region when $q_a = 3.367$![]() . Rotation number profile for (c) $q_a=3.365$
. Rotation number profile for (c) $q_a=3.365$![]() and (d) $q_a = 3.367$
and (d) $q_a = 3.367$![]() . The remaining parameter values are the same as in figure 2. This scenario exemplifies a bifurcation of shearless curves by collisions of periodic points (saddle–centre). The red and blue curves collide and mutually annihilate.
. The remaining parameter values are the same as in figure 2. This scenario exemplifies a bifurcation of shearless curves by collisions of periodic points (saddle–centre). The red and blue curves collide and mutually annihilate.
5. Conclusions
Shearless transport barriers have been identified in a theoretical model describing the $\boldsymbol {E}\times \boldsymbol {B}$![]() drift motion of the guiding centres. These barriers may be one of the mechanisms that hide behind certain improved scenarios observed in tokamaks with non-monotonic plasma profiles. Three profiles have been specified in advance, following experimental evidence: the safety factor radial profile, the average radial electric field profile and the toroidal velocity profiles. Excepting toroidal velocity, those profiles are non-monotonic and thus present some kind of reversed shear, the combined effect of them being the key ingredient in our model.
drift motion of the guiding centres. These barriers may be one of the mechanisms that hide behind certain improved scenarios observed in tokamaks with non-monotonic plasma profiles. Three profiles have been specified in advance, following experimental evidence: the safety factor radial profile, the average radial electric field profile and the toroidal velocity profiles. Excepting toroidal velocity, those profiles are non-monotonic and thus present some kind of reversed shear, the combined effect of them being the key ingredient in our model.
The equilibrium configuration characterized by these non-monotonic profiles is perturbed by the influence of electrostatic fluctuations with a dominant mode, whose amplitude was also determined from experimental results for the TCABR tokamak. Our results follow by numerical integration of the drift motion equations taking into account the reversed-shear profiles as well as the electrostatic fluctuation field. Since the motion equations were expressed in action–angle variables, the drift motion has a Hamiltonian form, and the Poincaré sections (taken at integer multiples of the dominant mode of the perturbation period) are actually area-preserving maps of a non-integrable system.
Since the radial profiles used are non-monotonic, this is a non-twist system, and hence some novel features are expected with respect to models using monotonic profiles. One of them is the existence of shearless curves, located at extrema of the rotation number profiles (in action space, which is essentially the radial direction).
The main result of our work was the discovery of multiple shearless curves when one of the system parameters (namely the safety factor at the plasma edge) is varied in specified intervals. These intervals comprise the neighbourhood of $q_a = 3$![]() equilibrium magnetic surface and thus are of physical interest since many tokamaks (including TCABR) operate at that range. Such multiple shearless curves can appear and disappear due to shearless bifurcations since they occur after (or before) the control parameter passes through critical values.
equilibrium magnetic surface and thus are of physical interest since many tokamaks (including TCABR) operate at that range. Such multiple shearless curves can appear and disappear due to shearless bifurcations since they occur after (or before) the control parameter passes through critical values.
We identified three groups of shearless bifurcations. In the first group, we have shearless curves that simply break up and reappear, indicating local changes in the rotation number profile (figures 5 and 6). Additionally, a partial transport barrier may still persist after the shearless curve breakup. In fact, small variations in the system parameters affect substantially the transport coefficients in such situations due to the configuration of cantori, LCS and escape channels by turnstiles. Furthermore, other mechanisms are relevant for the reduction of transport coefficients of non-twist systems, such as manifold crossing.
In the second bifurcation group, new shearless curves appear in phase space, after a saddle–centre bifurcation and the emergence of secondary twin island chains (figures 7 and 8). These curves are related to extrema of the rotation number profile, but one of them corresponds to a local minimum, while the other one to a local maximum. Finally, the third group involves the collision and disappearance of shearless curves, due to a bifurcation in the rotation number profile (figure 9) characterized by maximum and minimum points colliding as the control parameter is varied.
Depending on the strength of the fluctuation amplitudes, Poincaré sections show the existence of chaotic orbits on both sides of the shearless curves, indicating a limited extension of the chaotic transport in this region. In this case, when a shearless barrier breaks up, the chaotic orbits often merge together, leading to global transport. If there is more than one shearless curve, however, we can have two regions where the chaotic transport is reduced, increasing the complexity of the description. Since multiple ITBs have been actually verified experimentally, our work sheds some light on the nature of this dynamic phenomenon.
Acknowledgements
The authors thank Phil Morrison for fruitful discussions over the years. It is a pleasure for us to acknowledge his inspiring works and wish him many happy and fruitful years ahead.
Editor Paolo Ricci thanks the referees for their advice in evaluating this article.
Funding
The authors are grateful for financial support from the Brazilian Federal Agencies (CNPq) under grant nos. 407299/2018-1, 302665/2017-0, 403120/2021-7 and 301019/2019-3; the São Paulo Research Foundation (FAPESP, Brazil) under grant nos. 2018/03211-6, 2022/04251-7 and 2022/05667-2; and support from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) under grant nos. 88887.522886/2020-00 and 88881.143103/2017-01 and Comité Français d'Evaluation de la Coopération Universitaire et Scientifique avec le Brésil (COFECUB) under grant no. 40273QA-Ph908/18.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Normalization of variables in the drift-wave model
In this appendix, we outline the normalization of variables of the drift-wave model used in this paper, namely $B$![]() , $a$
, $a$![]() , $\omega _0$
, $\omega _0$![]() , $\overline {E_r}$
, $\overline {E_r}$![]() , $\phi _n$
, $\phi _n$![]() and $v_{\|}$
and $v_{\|}$![]() . Note that SI units are used throughout. The minor plasma radius, $a$
. Note that SI units are used throughout. The minor plasma radius, $a$![]() , is divided by the factor $a_0=0.18$
, is divided by the factor $a_0=0.18$![]() m, so the normalized value $a'=a/a_0 = 1$
m, so the normalized value $a'=a/a_0 = 1$![]() . Besides the normalization of the plasma radius, the TCABR tokamak aspect ratio $\epsilon =0.3$
. Besides the normalization of the plasma radius, the TCABR tokamak aspect ratio $\epsilon =0.3$![]() is maintained. The same is done for the toroidal field: we choose $B_0=1.1$
is maintained. The same is done for the toroidal field: we choose $B_0=1.1$![]() T $\Rightarrow$
T $\Rightarrow$![]() $B'=B/B_0=1$
$B'=B/B_0=1$![]() . We adopt an electric field normalization factor so that its magnitude has a unit absolute value at the plasma edge: $E_0 = |\overline {E_r}(r=a)|$
. We adopt an electric field normalization factor so that its magnitude has a unit absolute value at the plasma edge: $E_0 = |\overline {E_r}(r=a)|$![]() . Here
. Here
where $\alpha =-80\,{\rm kV}\,{\rm m}^{-3}$![]() , $\beta =31.95\,{\rm kV}\,{\rm m}^{-2}$
, $\beta =31.95\,{\rm kV}\,{\rm m}^{-2}$![]() and $\gamma =-6\,{\rm kV}\,{\rm m}^{-1}$
and $\gamma =-6\,{\rm kV}\,{\rm m}^{-1}$![]() . Thus, $E_0=2274\,{\rm V}\,{\rm m}^{-1}$
. Thus, $E_0=2274\,{\rm V}\,{\rm m}^{-1}$![]() and the normalized field, in action variables, is
and the normalized field, in action variables, is
therefore,
with $(\alpha ',\beta ',\gamma ') = (-1.140, 2.529, -2.639)$![]() .
.
The velocity, time and electric potential normalization factors are given by $v_0 = E_0/B_0 = 2067$![]() m s$^{-1}$
m s$^{-1}$![]() , $t_0 = a_0/v_0 = 8.707\times 10^{-5}$
, $t_0 = a_0/v_0 = 8.707\times 10^{-5}$![]() s and $\phi _0 = a_0E_0 = 409.3$
s and $\phi _0 = a_0E_0 = 409.3$![]() V, respectively, whereas the lowest angular frequency is $\omega _0=6\times 10^4$
V, respectively, whereas the lowest angular frequency is $\omega _0=6\times 10^4$![]() rad s$^{-1}$
rad s$^{-1}$![]() , such that its normalized value is given by $\omega '_0 = \omega _0 t_0 = 5.224$
, such that its normalized value is given by $\omega '_0 = \omega _0 t_0 = 5.224$![]() .
.