1. Introduction
The components of the surface mass balance of a snow/ice surface (SMB (kgm_2 or mmw.e.)) are solid precipitation (PR), surface sublimation/deposition (SUs) melt (ME) and processes related to drifting snow, namely erosion/deposition due to divergence/convergence of the horizontal snowdrift transport (ERds) and sublimation of drifting-snow particles in a column extending from the surface to the top of the drifting-snow layer (SUds):
All terms are defined as negative when they remove mass from the surface. In Antarctica, measuring surface mass balance components separately is a difficult task: precipitation gauges do not work well when snow falls under highwind-speed conditions, as is often the case in Antarctica, as drifting snow may enter the gauge (Reference BromwichBromwich, 1988). That is why, to date, no reliable estimates of the precipitation distribution over Antarctica exist, even though it is the dominant term in the surface mass balance (Reference King and TurnerKing and Turner, 1997).
Surface sublimation (SUs) is usually regarded as a process of intermediate importance for the surface mass balance of Antarctica. Measurements of SUs by weighing snow samples cannot be made at unmanned sites, but this method, applied to short periods of time, can yield valuable validation data for models (Reference FujiiFujii, 1979; Reference KaserKaser, 1982). SUs has been measured using eddy-correlation equipment during summer campaigns (Reference BintanjaBintanja, 2000), but the most common method remains to calculate SUs from profile measurements in the atmospheric surface layer, using Monin_Obukhov similarity theory. From published Antarctic surface sublimation data, a picture emerges of surface temperature being the controlling variable (Reference LiljequistLiljequist, 1957; Reference SchlatterSchlatter, 1972; Reference CarollCaroll, 1982; Reference Fujii and KusunokiFujii and Kusunoki, 1982; Reference Ohata, Ishikawa, Kobayashi and KawaguchiOhata and others, 1985; Reference Clow, McKay, Simmons and WhartonClow and others, 1988; Reference Wendler, Ishikawa and KodamaWendler and others, 1988; Reference Stearns, Weidner, Bromwich and StearnsStearns and Weidner, 1993; Reference Bintanja and van den BroekeBintanja and Van den Broeke, 1995; Reference Bintanja, Jonsson and KnapBintanja and others, 1997; Reference King, Anderson and MannKing and others, 2001; Reference Reijmer and OerlemansReijmer and Oerlemans, 2002). Weak deposition is often observed during the Antarctic winter (Reference King, Anderson, Smith and MobbsKing and others, 1996), while in summer surface sublimation may remove a significant part of the precipitated snow. Reference Van den BroekeVan den Broeke (1997) used data from a high-resolution general circulation model to estimate that SUs removes 10-15% of the annually precipitated snow, when averaged over the ice sheet.
Surface melting (ME) occurs mainly during summer in the coastal regions of Antarctica roughly below 2000ma.s.l. (Reference Liston, Winther, Bruland, Elvehøy and SandListon and others, 1999). Longer-lasting events have been observed on the ice shelves in the Antarctic Peninsula (Reference Schneider and SteigSchneider and Steig, 2002). The meltwater ponds that form on these ice shelves may ultimately lead to ice-shelf collapse (Reference Scambos, Hulbe, Fahnestock and BohlanderScambos and others, 2000).
If friction velocity (u*) exceeds a certain threshold value (u*t), snow particles are picked up from the surface and become suspended in the air. This phenomenon is called ‘drifting snow’ if the depth of the suspended snow layer is below eye level; otherwise the term ‘blowing snow’ is used. Erosion/deposition by divergence/convergence in the drifting-snow transport (ERds) is difficult to measure: a network of snowdrift instrumentation would be needed because the drifting process is too complicated to be captured by ordinary meteorological sensors. Reference King and TurnerKing and Turner (1997) showed that expressions that relate snowdrift transport rates to wind speed could yield differences of one to several orders of magnitude. It is generally acknowledged that this term can become locally very large and probably is responsible for the formation of Antarctic blue-ice areas in mountainous regions (Reference TakahashiTakahashi, 1988; Reference TakahashiTakahashi and others, 1988; Reference Van den Broeke and BintanjaVan den Broeke and Bintanja, 1995). Pettré and others (1986) argue that, away from the mountains, there also is an important interaction of katabatic winds, erosion and mass balance in Antarctica. For the ice sheet as a whole, ERds is probably of smaller significance;Reference Loewe and RadokLoewe (1970) estimated that 6% of the annual precipitation is blown from the ice sheet by katabatic wind, but more recently Dery and Yau (2002) estimated that this process is about two orders of magnitude less important than snowdrift sublimation.
SUds represents sublimation of suspended snow particles, which occurs when the ambient air is undersaturated with respect to ice (Reference SchmidtSchmidt, 1982). In steady state, the sublimated mass is resupplied from the surface by particles entering the suspension layer, so SUds represents a definite negative term in the surface mass balance. Snowdrift sublimation is more effective than surface sublimation, because, once airborne, snow particles expose more of their surface area and are more effectively ventilated than on the ground. Blowing-snow models show that significant amounts of snow may be removed from the Antarctic snow surface by this process, at least when ambient relative humidity is held constant at a value significantly below 100% (Reference BintanjaBintanja, 1998). However, measurements show that the moistening and cooling effect of the sublimation process quickly saturates the surrounding air (Reference Déry, Taylor and XiaoDéry and others, 1998; Reference Mann, Anderson and MobbsMann and others, 2000), so that only at the top of the blowing-snow layer, where the particles are smaller and fewer than near the surface, does snowdrift sublimation persist. Thus, for significant sublimation to proceed throughout the column, dry air must be entrained vertically or horizontally into the blowing-snow layer, or the air must be (adiabatically) heated and stay undersaturated (Reference Bintanja and ReijmerBintanja, 2001a).
Given the difficulty of measuring the various mass-balance components separately, it is usual to resort to measuring the specific surface mass balance (i.e. the mass balance integrated over a year), either with stakes to obtain year-to-year values or with snow cores for a period- integrated value of surface mass balance. With precipitation falling as snow throughout the year, the specific surface mass balance in Antarctica is generally positive, ranging from 300 to 800 mm w.e. a-1 near the coast to <50 mm w.e. a-1 on the inland plateau (Reference Vaughan, Bamber, Giovinetto, Russell and CooperVaughan and others, 1999).
A relatively new way to monitor the Antarctic surface mass balance is by way of acoustic height rangers mounted on automated measuring platforms (Reference Reijmer and van den BroekeReijmer and Van den Broeke, 2003). The obvious advantage of this method is that individual accumulation/ablation events are monitored; a disadvantage is that no reliable method is yet available to measure simultaneously the density of the accumulated/ablated snow, so that a conversion from height to mass change remains uncertain. In this paper, we use data from four automatic weather stations (AWSs) to study the components of the Antarctic surface mass balance. These AWSs are equipped with a sonic height ranger and situated in various climate zones of Antarctica. After a description of methods in section 2, we present the moisture climate at the AWS sites in section 3, followed by estimates of surface sublimation, melt and drifting-snow sublimation in section 4 and a discussion in section 5.
2. Methods
2.1 AWS description and sensor specifications
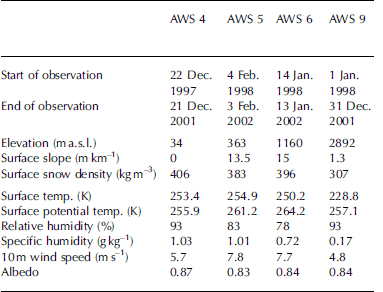
The AWSs in western Dronning Maud Land (DML), East Antarctica, are situated along a traverse line connecting the coastal ice shelf (AWS 4) to the polar plateau (AWS 9) via the katabatic wind zone (AWSs 5 and 6) (Fig. 1):

Fig. 1. Map of western Dronning Maud Land, Antarctica, with AWS and station locations (filled squares), main topographical features, ice shelves (grey) and height contours (dashed lines, equidistance 100 m).
AWS 4 (72°45.2’ S, 15°29.9’ W; 34 m a.s.l.) is located on the Riiser-Larsen Ice Shelf some 80 km from the sea and 40 km from the grounding line.
AWS 5 (73°06.3’S, 13°09.9’W; 363 m a.s.l.) is located on the coastal slopes of the ice sheet, just inland of the grounding line.
AWS 6 (74°28.9’S, 11°31.0’W; 1160m a.s.l.) sits at the foot of the Heimefront Mountains in the katabatic wind zone.
WS 9 (75°00.2’ S, 0°00.4’ E; 2892 m a.s.l.) is situated on Amundsenisen on the East Antarctic plateau.
The surroundings of the AWS consist of undisturbed snow surface. In this part of Antarctica, the transition from thepolar plateau to the coast occurs in two stages: the Heimefront Mountains represent a steep transition from 2500 to 1200ma.s.l., then there is a more gradual slope towards the ice-sheet grounding line. The large-scale surface slopes included in Table 2 are taken from Reference Reijmer and OerlemansReijmer and Oerlemans (2002)
All four AWSs are similar in design; a picture of AWS 9 is shown in Figure 2. The AWSs measure wind speed and direction, temperature (T) and relative humidity (RH), and down- and upward short- and longwave radiation fluxes (SHW↓, SHW↑, LW↓, LW↑) at a single level approximatelym above the ground at the date of installation. Air pressure (p) is measured in the electronics enclosure that is buried in the snow. Snow temperatures are measured at initial depths of 0.05, 0.1, 0.2, 0.4 and 0.8 m. These depths, as well as the height of the AWS instruments, change continuously as snow accumulates or is ablated from the surface. These height/depth changes are monitored with a sonic height ranger. The sampling frequency for pressure is 30min (instantaneous value); all other sensors are sampled at 6min intervals (instantaneous, except for wind speed (cumulative)), after which 2 hour averages are calculated and stored in a Campbell CR10 datalogger. Energy considerations do not allow aspiration of the temperature/humidity sensors and/or heating/ventilation of the radiation sensors. On-site comparisons with ventilated instruments show that radiation errors in the T/RH readings do not exceed the uncertainty arising from instrument accuracy. Treatment of the radiation data (needed for energy-balance calculations in the case of melt; see below) is described in detail in Van den Broeke and others (2004). Sensor specifications are summarized in Table 1.

Fig. 2. Picture of AWS 9, taken 4years after installation, i.e. after approximately 1 m of snow accumulation. The datalogger and pressure sensor are buried in the snow. The other AWSs have similar designs. T is temperature, RH relative humidity.
Table 1. Table 1. AWS sensor specifications (EADT: estimated accuracy of daily totals)<image>

2.2 Correction of relative humidity at low temperatures
Correct measurement of the air moisture content is vital for calculating sublimation. The Vaisala HMP35AC instrument incorporates the Humicap, a capacitive device that is calibrated in the factory to measure RH with respect to water (RHw). This leads to unrealistic values of RH at freezing temperatures, with a clear cut-off at values significantly below 100%. An example of this is given for AWS 6 inFigure 3a. To remedy this, a two-step correction to the RH data was applied along the lines of Reference AndersonAnderson (1994). First, all RHw values are multiplied by the ratio of the saturated vapour pressures over water and over ice (es, w/es, i) to obtain RH with respect to ice, RHi. We use the expression of Reference Curry and WebsterCurry and Webster (1999) to calculate es (subscript i: over ice; subscript w: over water) from temperature T:

Fig. 3. Relative humidity (2 hour averages) at AWS 6, 1998-2001, as a function of temperature, (a) with respect to water (RHw), (b) with respect to ice (RHi), and (c) rescaled (see text).
where Lsub = 2.8 106 J kg_1 is the latent heat of subli1mation and Lvap = 2.50 106 J kg_1 the latent heat of evaporation, both assumed constant, T 0 and e 0 are temperature and water-vapour pressure at the freezing point of water (611 Pa)and is a constant equal to 2317. The result of this first step is to increase substantially the RH values at values below 08C (Fig. 3b). However, at T _208C, the corrected data still have an upper cut-off because they are outside thetemperature calibration range of the instrument. In the second correction step all RHi values are binned in 1 K intervals, after which a polynomial function is fitted to the 98th percentile. This fit is used to correct the data upwards to 100% RHi (Fig. 3c). This allows for 2% occasional spuriously high values, not for supersaturation, which, because of its design, the Humicap cannot measurem(Reference MakkonenMakkonen, 1996). Because Reference AndersonAnderson (1994) notes that the cut-off error is in the gain of the instrument rather than being an offset, the upward correction is scaled by the original value (e.g. a measured RHi of 0% would remain unaltered by this procedure). RH sensors at all AWSs are replaced on average once every 2 years, and the procedure described here has been applied to the data from each individual sensor.
Recent studies question the reliability of the Humicap sensor in cold environments. Comparing measurements of the Vaisala HMP35AC and a dew-cell hygrometer in the Canadian Arctic, Dery and Stieglitz (2002) showed that the HMP35AC has a strong tendency to measure saturation values, probably due to icing of the sensor housing. Observations at Halley, Antarctica, suggest that deviations in both directions may occur (Reference King and AndersonKing and Anderson, 1999). We know that icing of the sensor housing does occur at our AWS, so the RH readings may be expected to be unreliable at times. However, comparison experiments at the AWS 6 and AWS 9 sites in summer, when sublimation is significant, show excellent agreement between unventilated and ventilated T/RH measurements. Moreover, significant undersaturation is observed at the AWS in the katabatic wind zone throughout the year (see section 5). Comparing with frost-point hygrometer readings at Halley, Reference AndersonAnderson (1996) moreover concludes that rescaled RHi measurements with the Vaisala HMP35A are reassuringly good down to -40°C. We therefore accept our rescaled RHi data without further selection, and use them to calculate specific humidity q:
where Rd and Rv are the gas constants for dry air and water vapour, respectively.
2.3 Calculation of surface sublimation (SUs)
Surface sublimation SUs (kgm-2s-1) is derived from the surface turbulent moisture flux LHFs using SUs = LHFs/Lsub. LHFs follows from:
where u*, q* are the turbulent scaling parameters of momentum and moisture, and p is the density of the nearsurface air. The turbulent scaling parameters are calculated using the robust ‘bulk’ method (Reference Denby and GreuellDenby and Greuell, 2000), which relates the turbulent scales to differences in wind speed, potential temperature and specific humidity between the single AWS measurement level and the snow surface according to:


where θ* is the turbulent scaling parameter of heat, k is the von Kärmän constant (k = 0.4), and V, q and θ are wind speed, specific humidity and potential temperature measured at heights zv, zq and zT, respectively. The RH and T sensors are in the same housing, so zq = zj, while zv is greater by about 0.75 m (Fig. 2). Note that the absolute values of zv, zq and zj change continuously in time due to accumulation/ablation at the snow surface Ψm and Ψh are the stability functions for momentum and heat/moisture, respectively. They are a function of the Monin-Obukhov length scale L MO, given in Equation (6). For stable conditions (z/Z.MO>0), we use the m and functions proposed by Reference Holtslag and de BruinHoltslag and de Bruin (1988), which behave most consistently in the very stable limit where turbulence ceases (Reference AndreasAndreas, 2002). For unstable conditions (z/L MO < 0) the functions of Reference DyerDyer (1974) are used. Because L MO itself depends on the turbulent scales, Equations (5) and (6) are solved iteratively.The surface roughness lengths for momentum (z 0, v), specific humidity (z 0, q) and temperature (z 0 T) are defined as the levels where V, q and 0 extrapolate towards their surface values. It is well known that the (apparent) roughness length increases when snowdrift occurs (Reference SchmidtSchmidt, 1986; Reference Wamser and LykossovWamser and Lykossov, 1995; Reference Mann, Anderson and MobbsMann and others, 2000; Reference Bintanja and ReijmerBintanja, 2001c). Turbulence measurements during near-neutral and non-snowdrift conditions (|z/L Mo < 0.1, u.03ms-1) atthe AWS 6 and AWS 9 sites yielded Z 0, v values of 0.16 and 0.021 mm, respectively. For ease of comparison, we use z 0, y = 0.1 mm for all AWSs in the control run, and later on investigate the sensitivity to changes in z o, v. Based on a surface renewal model, in which eddies continuously scour the surface exchanging heat and moisture, Reference AndreasAndreas (1987) related z 0, q and z 0, T to z 0 v through the roughness Reynolds number Re. = u. z 0 z -1:

where v is the kinematic viscosity of air (a function of air density) and c 1-c6 are constants given in Reference AndreasAndreas (1987). The expressions summarized in Equation (7) are valid for rough flow (Re*>2.5);below this value a linear transition towards smooth flow is prescribed (Re*<0.135), in which z0 q and z0— are constants. Reference AndreasAndreas (2002) presents additional experimental evidence for the validity of Equation (7) over snow. Note that over snow typically z 0, v << z v, z 0, q << zq and z 0, T << z T, so that the third terms in the denominator of Equation (5) are very small corrections.
By definition V (z 0 V) = 0, and we assume the snow surface to be saturated with respect to ice, i.e. RHi (z 0, q) = 100% so that q (z 0, q) = q si, (T s), where subscript s refers to surface values. We take observed pressure as reference pressure in the calculation of θs so that θs — T s. To close the problem we need T s = T(z 0, T), for which we use LW↑:
where σ = 5.67x 10-8Wm-2K-4 is the Stefan-Boltzmann constant and where the surface longwave emissivity is set to 1. Van den Broeke and others (2004) showed that the AWS radiation sensors perform much better than their factory specifications as listed in Table 1. For LW↑, better than 4Wm-2 (1 K) accuracy is achieved when 2 hourly averages are considered, as here. Figure 4 compares LHFs values calculated using the method outlined above with a week of eddy-correlation measurements that were performed next to AWS 6 in January 1998 (Reference BintanjaBintanja, 2000).Based on 2 hour averages, the calculated LHFs agrees well with the observations (R — 0.98, rmse — 2Wm-2).

Fig. 4. Comparison of 2 hour average calculated and directly measured surface latent-heat flux LHFS, for a 1 week period at AWS 6 in January 1998.
2.4 Calculation of melt (ME)
When the snow surface reaches the melting point, the full (skin-layer) surface energy balance is calculated to quantify the melting energy M:
where a is surface albedo, SHF the turbulent flux of sensible heat, and G s the subsurface conductive heat flux. Penetration of shortwave radiation into the snowpack is neglected, which is justified for dry, fine-grained Antarctic snow (Reference Brandt and WarrenBrandt and Warren, 1993). All terms are defined positive when directed towards the surface. The surface melt rate follows from ME = M/Lf, where Lf is the latent heat of fusion (L f0.34 × 106 Jkg-1). Below the surface we take into account in a simple fashion the percolation and refreezing of meltwater.
2.5 Calculation of column snowdrift sublimation(SUdS)
Recently, several numerical models of blowing-snow sublimation have been developed and compared (Reference Xiao, Bintanja, Déry, Mann and TaylorXiao and others, 2000). All these models explicitly solve for snowdrift sublimation as a function of height and time in a number of particle size classes. From these complex models, simple parameterizations have been derived to calculate total column snowdrift sublimation as a function of (single-level) measurements of wind speed, temperature and relative humidity. Here, we use the expressions proposed by Reference Bintanja and ReijmerBintanja and Reijmer (2001) and Reference Déry and StieglitzDéry and Yau (2001), hereafter referred to as BR01 and DY01. The expression of DY01 needs as input 2 m T and RHi and 10 m wind speed. We correct AWS wind speed to a 10m value using the flux profile relations, but neglect T and RHi differences between 2 m and the AWS sensor height. Reference BintanjaBintanja (1998) proposed a third parameterization similar to DY01, but he assumed a constant ambient RHi of 70%. Judging from our RHi observations (see Fig. 2), this would lead to an overestimation of snowdrift sublimation, so we decided not to use this expression.
The method of BR01 is based on the observation that the values of z 0, v z 0, T— and z 0, q increase when snowdrift starts (Reference Wamser and LykossovWamser and Lykossov, 1995; Reference Mann, Anderson and MobbsMann and others, 2000; Reference Bintanja and ReijmerBintanja, 2001c). BR01 thus present expressions to calculate new values for z 0, v z0— and z 0, q as a function of u*, after which total column sublimation follows from the flux profile relations. Since u* depends on z 0, v a new value of u* is obtained in an iterative fashion. We neglect stability effects, as the profile functions are no longer valid in the presence of a moisture source and heat sink, and furthermore impose an upper limit on z 0, v z0— and z 0, q of 0.1 m, as this is the approximate maximum value for z 0 q for which BR01 was derived (corresponding to a value of u* of approximately 0.8 m s-1).
For all snowdrift sublimation calculations, we use a threshold friction velocity of 0.3 m s-1 and assume that surface sublimation stops when snowdrift (sublimation) starts. This is based on the observation that, once drifting snow starts to sublimate, the near-surface air, where drifting particles are most abundant, quickly becomes saturated with respect to ice.
2.6 Calculation of surface mass balance from sonic height ranger observations
The data from the sonic height ranger are used to calculate surface mass balance at the AWS site as a function of time. To obtain water equivalents, height changes are multiplied by the average density of the accumulated snowpack since the last visit (Table 2). Given the density variations in the upper snowpack, we estimate that this yields an uncertainty in instantaneous surface mass-balance values of 15%.
Table 2. AWS topographic and climate characteristics, 1998-2001. If no height is specified, the mean value at AWS sensor level is used
3. Moisture Climate and Latent-Heat Fluxes
In this section, we discuss the general moisture climate at the AWS sites, including surface and snowdrift latent-heat fluxes. Table 2 lists annual mean values of basic climate variables, Figures 5-9 present daily mean values of temperature and moisture variables for the period 1998-2001.

Fig. 5. Daily means of surface temperature 7 S, 1998-2001, at (a) AWS 4, (b) AWS 5, (c) AWS 6 and (d) AWS 9.

Fig. 6. Daily mean values of relative humidity with respect to ice (RH|, ), 1998-2001, at (a) AWS 4, (b) AWS 5, (c) AWS 6 and (d) AWS 9
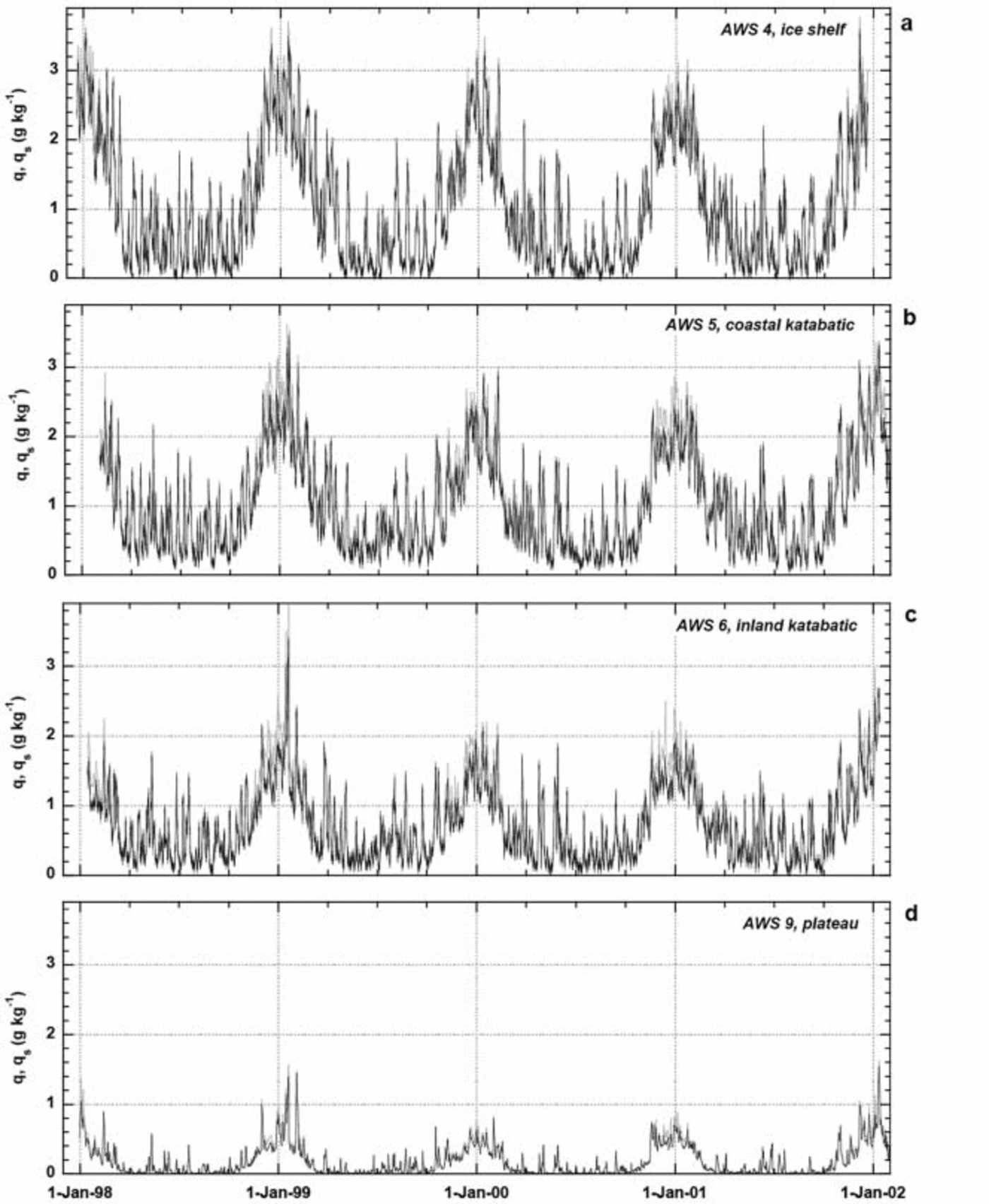
Fig. 7. Djiiot cifK humklhy if bbii, line) and sirixe specific humidry 9 (grey line). I99A 2001, t (d) AWS4, (b) AWS 5, c) AWS 6 and (d) AWS 9.

Fig. 8. DaiK’ mr-in* i* writer btcsitJioaf flux (IHFJ, vatfi inclusion (if vmvdrifi i_L_:k lino) atif withouT inclusion ci itinvdriti (flrrry linri. I_a 2001, atfalAWS * (b) AWS 5, (tl AWS 6 anct (d) AW5 9.

Fig. 9. Daily means of drifting-snow latent-heat flux (LHFds), average of two methods (see text), 1998_2001, at (a) AWS 4, (b) AWS 5, (c) AWS 6 and (d) AWS 9.
3.1 Temperature
Absolute temperature is a very important moisture- and sublimation-controlling variable. The average surface temperature T s at AWS 4 is 253.4 K, comparable to the 2 m temperature at nearby ice-shelf stations like Halley (253.7 K) and Neumayer (257.0 K) but 8-10 K lower than 2 m temperature at coastal stations further east (Syowa, Mawson and Casey). The main reason for the cold ice-shelf climate is the frequent formation of a surface-based temperature inversion, whereas coastal stations further east are under the direct influence of katabatic winds that prevent the formation of a strong surface inversion (Reference Van den Broeke and van LipzigVan den Broeke and Van Lipzig, 2003. Katabatic winds generate turbulence through enhanced wind shear in the stably stratified surface layer, mixing relatively warm air towards the surface, causing so-called warm surface signatures (Reference BromwichBromwich, 1989; Reference Van den BroekeVan den Broeke and others, 1999). This leads to higher air temperatures and lower relative humidity in the katabatic wind zone. Owing to surface friction, katabatic winds in Antarctica have a downslope component only near the ground (Reference Van den Broeke, van Lipzig and van MeijgaardVan den Broeke and others, 2002), further heating the near-surface air through adiabatic compression. In our array of AWSs, the influence of katabatic winds is visible through elevated 10 m wind speeds and potential temperatures at the locations with a significant surface slope (AWSs 5 and 6;see Table 2).
Figure 5a-d show daily mean T s at the four AWSs for the period 1998-2001. All stations show frequent signatures of warm-air intrusions. At AWS 9, T s may rise 40 K in 2 days, signifying the complete removal of the surface-based temperature inversion under the influence of increased cloudiness, strong winds and the advection of warm air. The seasonal amplitude is greater at AWSs 4 and 9 (40-45 K) than at AWSs 5 and 6 (30-35 K). This is again due to the stronger surface temperature inversion at AWSs 4 and 9, a sign of weak or absent katabatic winds. When during summer the radiation balance becomes positive under the influence of shortwave radiation absorption, the temperature inversion and the temporal variability of T s become small at all AWSs.
3.2 Relative and specific humidity
Differences between katabatic and non-katabatic locations are obvious from the means (Table 2) and time series of RHi (Fig. 6a-d). Mean RHi at AWSs 4 and 9 is 93%;only during summer and sporadically during winter does daily averaged RHi fall below 80%, but it never falls below 70% (Fig. 6a and d). Average RHi at AWSs 5 and 6 is lower by 10-15%, with a much less pronounced seasonal cycle (Fig. 6b and c); significant undersaturation occurs year-round, with daily mean values as low as 45% occurring at AWS 6. It is likely that the somewhat higher values of RHi at AWS 5 compared to AWS 6 are caused by surface sublimation, feeding moisture into the descending air. A qualitative interpretation of the data presented in Table 2 is that cold plateau air (near to saturation) becomes undersaturated when it descends, and heats up when flowing coastward. In the katabatic wind zone, relatively strong surface sublimation slowly increases relative humidity. If the air arrives at the ice shelf, vertical movement stops and mixing decreases; radiative cooling quickly returns the air to near-saturation. Heat- and moisture- budget calculations must confirm this mechanism.
Figure 7a-d show specific humidity q, both at sensor height (black lines) and at the surface (grey lines). Seasonal variations in q at AWSs 4 and 9 are mainly controlled by variations in temperature and less so by RHi, given that the highest values of q occur during summer (Fig. 7a and d) in spite of the relatively low RHi in summer (Fig. 6a and d). Variations in RHi explain second-order differences in q, such as the slightly lower q values at AWS 5 compared to AWS 4 in spite of the somewhat higher temperatures (Table 2). In winter, sharp temporal variations in q and T occur simultaneously, signifying advection of warm and humid air masses. The low summertime temperatures at AWS 9 do not allow for q, q s values in excess of 1.5 gkg-1.
The vertical gradient of q (difference between black and grey lines in Fig. 7) peaks in summer, when absorption of solar radiation raises T s and q s, while the relative humidity of the air is low. The importance of shortwave radiation absorption is confirmed by the absence of similar moisture gradients during warm-air intrusions in winter, even though q may attain comparable values (Fig. 7). The largest bulk gradients of q are found in summer at AWSs 5 and 6 and not at AWS 4, because both RHi and albedo are lower in the katabatic wind zone (Table 2). The high albedo at AWS is caused by the frequent occurrence of clouds and precipitation (Reference Van den Broeke, van, Reijmer and Van de WalVan den Broeke and others, 2004). Clouds raise the albedo by altering the spectral distribution of shortwave radiation that reaches the surface (Reference Brandt and WarrenBrandt and Warren, 1993), while fresh snow has a relatively small grain-size, which increases the albedo (Reference Wiscombe and WarrenWiscombe and Warren, 1980). Temperatures at AWS 9 are too low and RHi too high to enable large moisture gradients to develop, even in summer.
3.3 Surface latent-heat flux
Small mean latent-heat fluxes can still be important for the mass household of Antarctica: an annual average LHFs of only -1 W m-2 removes 11 kg m-2 of snow from the surface, which potentially is a significant fraction of the solid precipitation in the dry interior of Antarctica. Figure 8a-d show daily mean LHFs values, calculated with (black lines) and without (grey lines) the condition that LHFs = 0 during snowdrift. LHFs in summer attains values of 5-15 Wm-2 at AWSs 4-6, representing daily sublimation rates of 0.150.45 mm w.e. These values are similar to those calculated for the coastal station Halley (Reference King, Anderson and MannKing and others, 2001). At AWS 9, the magnitude of daily mean LHFs is generally <5Wm-2. During winter, the air is generally warmer than the surface, which may reverse the moisture gradient. As a result, LHFs is mostly weakly positive at AWSs 4-6, signifying deposition. However, the associated moisture fluxes are small due to the continuous saturation of the surface and the stable stratification of the surface layer. Sporadic surface sublimation events also occur in winter, especially at AWS 6 (Fig. 8c). The condition that LHFs = 0 during snowdrift removes high-magnitude events from the surface sublimation record (compare the black and grey lines). This reduces summer surface sublimation at AWSs 4-6, winter surface deposition at AWS 5 and winter surface sublimation at AWS 6. From the above it is clear that in Antarctica significant surface sublimation (LHFs<-10Wm-2) only occurs in summer at low elevations; only then and there is saturation specific humidity at the surface large enough to create significant moisture gradients between surface and air. At temperatures below 235 K the absolute value of q and therewith its gradient becomes so small that the magnitude of LHFs is always <1 W m-2.
3.4 Column snowdrift latent-heat flux
Figure 9a-d show daily mean column snowdrift sublimation (LHFds), averaged for the two methods DY01 and BR01. Major snowdrift sublimation events occur at all four AWSs, but most frequently at the katabatic AWSs 5 and 6 and least frequently at AWS 9. No clear seasonality can be detected. Typical maximum (negative) daily mean values range from 15 W m-2 at AWS 9 to 50-55 W m-2 at the other AWSs.
4. Surface Mass Fluxes
In this section, we divide the surface mass-balance signal from the sonic height rangers into its components SUs, SUds, ME and ‘residual processes’, which according to Equation (1) embodies PR and ERds. For the moment we assume the latter term is small, and ‘residual processes’ will henceforth be referred to as solid-precipitation PR. Cumulative surface mass-balance components over the period 1998-2001 are presented in Figure 10a-d, where we have set all fluxes to zero at 0000 h GMT on 4 February 1998, the start of the period that all four AWSs were operational. The average annual cycle of the mass-balance components, based on monthly means, is presented in Figure 11a-d, and annual mean mass fluxes are listed in Table 3.

Fig. 10. Cumulative mass fluxes, 1998-2001, of (a) surface mass balance (solid line) and ‘residual processes’ (PR + ER(js, dashed lines), (b) surface sublimation (SUS), (c) melt(vVI) and (d) column snowdrift sublimation (SU(is), for two methods (dashed lines) and average (solid line).
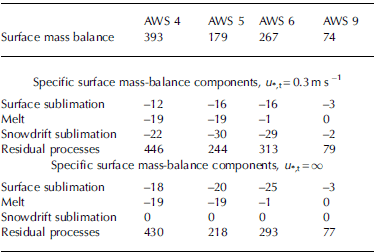
Table 3. Specific surface mass balance and components in mmw.e.a"1, 1998-2001
4.1 Surface mass balance and solid precipitation (PR)
The average specific surface mass balance for the period 1998-2001 ranges from 393 mm w.e. a-1 at AWS 4 to 74 mm w.e. a-1 at AWS 9 (Table 3). These values fall within the range reported from this area: accumulation rates derived from shallow firn cores yielded values of 64.0 mm w.e. a-1 for AWS 9, and 350-400 mm w.e. a-1 for the AWS 4 area.
PR is the sole accumulation term in the specific surface mass balance at all AWSs (Table 3). The fact that PR is greater at AWS 6 than at AWS 5 even though AWS 6 is farther from the coast underlines the importance of topographically forced precipitation in Antarctica: AWS 6 is situated at the foot of the steep transition to the plateau (Fig. 1), where maritime air masses must rise by >1500 m, releasing part of their moisture. Four years of data is too short a period for a seasonal cycle in PR to be detected (Fig. 11a). Reference Reijmer and van den BroekeReijmer and Van den Broeke (2003) describe in more detail the characteristics of accumulation in DML. In general we can say that significant precipitation events are most frequent at AWS 4, while sporadic events determine the accumulation characteristics at AWSs 5, 6 and 9 (Fig. 10a). At all AWSs, up to several months can pass without a significant precipitation event. During summer, the mass balance in these long dry periods is significantly negative, and quite often the snow accumulated in one event may be completely ablated before the next occurs. On an annual basis, Table 3 shows that all ablation processes together remove 12%, 27%, 15% and 6% of the precipitated snow at AWSs 4, 5, 6 and 9, respectively.

Fig. 11. Monthly mean values of mass-balance components, 1998-2001: (a) ‘residual processes’ (PR + ERds), (b) surface sublimation, (c) melt and (d) column snowdrift sublimation (averaged for the two methods DY01 and BR01).
4.2 Surface sublimation (SUs)
At all AWSs, SUs is a typical summer phenomenon and it attains its greatest values in the katabatic wind zone (Figs 10b and 11b; Table 3). On an annual basis, the mass loss associated with summer sublimation is partly offset by net deposition during winter (Fig. 10b), which occurs when intrusions of warm, moist air encounter the cold Antarctic snow surface. Summer sublimation is greatest at AWS 5, but relatively strong winter deposition makes net sublimation at AWSs 5 and 6 equal over the year (Table 3). At AWS 9, small but significant sublimation occurs in summer, but only in early and late summer are temperatures at this station sufficiently high to allow for detectable deposition (Figs 10b and 11b). On an annual basis, surface sublimation removes 3%, 7%, 5% and 4% of the annual precipitation at AWSs 4, 5, 6 and 9, respectively. Note that these mass fluxes correspond to annual mean LHFs of only -1.1, -1.5, -1.5 and -0.3 Wm-2. Surface sublimation leads to net ablation during prolonged dry periods, which is visible in Figure 10b as surface lowering during the summer months (e.g. summer 2000/01).
4.3 Melt (ME)
Because the latent heat of melting (Lf — 0.34 × 106 Jkg-1) is about eight times smaller than the latent heat of sublimation (L sub — 2.84 × 106 Jkg-1), relatively little melting energy is sufficient to obtain relatively large mass fluxes (Fig. 10c). Summer melting occurs regularly at AWSs 4 and 5, with December and January being the preferred months for melting (Fig. 11c). At AWS 5, small events are also detected in November and February. Melting shows large interannual variability: in summers with large events (e.g. 1997/98 and 1998/99), melting may be a more important ablation term than surface sublimation (Fig. 10c). On the other hand, in the summer of 1999/2000, melt was nearly absent. On average over the observation period, melting is as important an ablation term as surface sublimation at AWSs 4 and 5 (Table 3).
4.4 Column drifting-snow sublimation (SUds)
Figure 10d shows cumulative column drifting-snow sublimation calculated using BR01 and DY01 (dashed lines) and the average (solid line). Given the very different methodologies on which the two parameterizations are based, it is surprising that the cumulative mass fluxes are so similar, with differences after 4years being <20%. This gives someconfidence in the numerical outcome of these methods. The annual column snowdrift sublimation rates (Table 3) range from 2mmw.e. a-1 at AWS 9 to 22mmw.e. a-1 at AWS 4 and about 30mmw.e. a-1 at AWSs 5 and 6. Figure 11d shows that snowdrift sublimation, averaged for both methods, peaks in the summer months but, apart from AWS 9, persists throughout the year.
The annual values of SUds for AWSs 4-6 are comparable to the 30 mm w.e. a-1 calculated for Halley (Reference King, Anderson and MannKing and others, 2001). They also qualitatively agree with the values presented by DY01 and are similar in magnitude to direct measurements performed in the Canadian Arctic (Reference Pomeroy and EsseryPomeroy and Essery, 1999). Various studies suggest that SUs and SUds in Antarctica are of the same order of magnitude (Reference King, Anderson and MannKing and others, 2001; Dery and Yau, 2002), which agrees with the results presented here. On the other hand, our values are significantly smaller than those presented by Reference BintanjaBintanja (1998), who calculated values up to 175 mm w.e. a-1 for a coastal AWS in Terre Adelie. It is likely that his assumption of a constant ambient RHi of 70% inflated sublimation rates.
4.5 Summer balance
Because surface sublimation, melt and snowdrift sublimation all peak in summer, it is interesting to look at the surface mass balance for the summer period only, which we have chosen here as the months November-February. Table 4 lists the mass fluxes, expressed in mm w.e. d-1. At AWS 5, the relatively low precipitation rate in combination with relatively large ablation fluxes results in low net summer accumulation. In the four summer months, all ablation processes together remove 39%, 56%, 30% and 15% of the precipitated snow at AWSs 4, 5, 6 and 9, respectively.
Table 4. Average summer (November-February) surface mass fluxes in mm w.e. d-1, 1998-2001

5. Discussion
The purpose of this study is to demonstrate the potential of AWS data for mass-balance studies, not to provide definite mass-balance values; 4 years of data is clearly insufficient to calculate a reliable climatology or seasonal cycle of mass fluxes. In particular, the solid-precipitation PR shows very large interannual variability, and many more years of observations are needed before climatologically meaningful numbers can be derived from it. Moreover, the uncertainty in the magnitude of the mass fluxes presented here can also be considerable. Converting height changes to mass changes using an average density of the accumulated snowpack introduces an uncertainty of about 15%. To reduce this error, a device is needed that determines the mass of the accumulated snow in addition to the surface height change, so that the density of the near-surface snow can be determined. The melt values presented here are also rather uncertain, because they are determined as the residual of a full energy-balance calculation. We estimate the calculated melt fluxes to have a 30% uncertainty.
Even less well constrained are the calculated column snowdrift sublimation rates, which are merely order-of- magnitude estimates. It is encouraging to see that the two very different methods used in this study give comparable cumulative mass fluxes, but this may be partly fortuitous. As an example of disagreement between the two methods, we mention the seasonality in snowdrift sublimation, which is much greater for BR01 than DY01. This points towards a stronger temperature sensitivity of BR01, which reduces snowdrift sublimation rates in winter. In DY01 this sensitivity is to a great extent compensated by stronger wintertime winds. Both parameterizations also have obvious limitations when applied to AWS data. DY01 generates zero column snowdrift sublimation for RHi = 100% at AWS sensor level, while snowdrift sublimation may well be significant above this level. This also introduces an unwanted dependency on sensor height. Fortunately, because the drifting particle concentration decreases exponentially from the surface upward, the saturated layer is relatively shallow, typically 10cm for 2m wind speeds of 10ms-1 (Reference Bintanja and ReijmerBintanja, 2001b). Only in the strongest blowing-snow conditions will the saturated layer be thick enough to reach the sensor level, that is 1-3 m above the surface. The BR01 method circumvents this problem, but tends to generate unrealistically highcolumn drifting-snow sublimation rates at very high wind speeds if no limit is imposed on z 0, q. As a result, the choice for a limiting value for z0q is critical for the final result. In a combined empirical-theoretical model of column drifting- snow sublimation, Reference King, Anderson and MannKing and others (2001) matched profiles of particle concentration, temperature, relative humidity and wind speed to two-level observations of T, RHi and V. This method is much less sensitive to the errors described above, and in that respect is the preferred choice. However, as we have only a single measurement level at our disposal, profile fitting introduces uncertainties that render this more sophisticated model of limited value for application to single-level AWS observations.
Another important issue is the threshold friction velocity u*t which, contrary to the assumption made in this paper, is far from constant in space and time: new, fresh snow can start drifting at u*t as small as 0.1 ms-1 (Reference SchmidtSchmidt, 1982), but u*t quickly increases with progressive metamorphism of the surface snow (Reference Li and PomeroyLi and Pomeroy, 1997; Reference Gallée, Guyomarc’h and BrunGallee and others, 2001). This problem is illustrated in Figures 8a and 9a, where the arrow points towards a 2 day period at AWS 4 in January 1998 with anomalously large snowdrift sublimation, caused by a combination of strong winds and significant undersaturation of the air (daily mean RHi of 80%). This storm followed several days of melting at AWS 4, which must have strongly increased the cohesion between surface snow grains and subsequently limited the availability of snow for drifting, in spite of daily mean u* being in excess of 0.7 ms-1. In our calculations, because u*> u*t, this event is ascribed to snowdrift sublimation rather than surface sublimation, and this may well make them wrong.
The AWS data can be used to make some qualitative statements about u*t. In Antarctica, increasing wind speed causes a higher temperature because of the enhanced downward mixing of potentially warmer air. In the absence of local moisture sources, this will lead to a decrease in relative humidity. An increase in relative humidity from a certain wind speed onwards could thus imply the presence of sublimating snowdrift particles. Evidence that blowing- snow sublimation does occur at the AWS sites is provided by the increase in relative humidity at high wind speeds at all AWSs (Fig. 12). This increase must be caused by a moisture flux from drifting-snow particles to the air and/or a heat flux from the air to the drifting-snow particles. Figure 12 shows

Fig. 12. Scatter plot of daily mean RHj vs friction velocity u*, 1998-2001, at (a) AWS 4, (b) AWS 5, (c) AWS 6 and (d) AWS 9. Note reversed y axis.
Table 4. Average summer (November-February) surface mass fluxes in mm w.e. d-1, 1998-2001 that the value of u* from which relative humidity at sensor- arm level starts to increase ranges from 0.1-0.15 ms-1 at AWSs 4 and 9, to 0.20-0.25 m s-1 at AWSs 5 and 6. Figure 13 shows the cumulative occurrence of u* values at the AWS. If we assume u*t = 0.3 ms-1, snowdrift occurs 20%, 30%, 29% and 8% of the time at AWSs 4, 5, 6 and 9, respectively. However, if we use u*t = 0.15 m s-1 at AWSs 4 and 9 and u*t = 0.25 ms-1 at AWSs 5 and 6, these values increase to roughly 40% at all four AWSs.

Fig. 13. Cumulative occurrence of 2 hourly average friction velocity u* (1998-2001).
The results for surface sublimation SUs are quite robust. For instance, tripling z0 , V from 0.1 to 0.3 mm increases surface sublimation by 10-15%. A greater uncertainty is introduced by setting SUs to zero whenever snowdrift sublimation occurs; the lower part of Table 3 lists mass- balance components when no drifting snow is allowed (i.e. u„, t = 1). In this case, surface sublimation rates increase by 50%, 25% and 56% at AWSs 4, 5 and 6, respectively, and remain unchanged at AWS 9. However, total sublimation (SUs + SUds) decreases, from 34 to 18 mm w.e. a-1 at AWS 4, from 46 to 20 mm w.e. at AWS 5, from 45 to 25 mm w.e. at AWS 6 and from 5 to 3 mm w.e. at AWS 9. This confirms that snowdrift sublimation, when it occurs, is generally more effective than surface sublimation.
6. Summary and Conclusions
We used data from four AWSs in DML to study the Antarctic surface mass balance and its components. Distinct differences were found between the moisture climates of the high plateau, the katabatic wind zone and the coastal ice shelves: significant undersaturation occurs year-round in the katabatic wind zone, where air is adiabatically heated and therefore relatively dry and warm. On the high plateau as well as on the coastal ice shelf, weaker vertical mixing causes the air to be close to saturation for most of the time. In summer, absorption of shortwave radiation heats the snow surface, leading to relatively large surface-to-air moisture gradients, which enhance surface sublimation. Significant summer melting is detected at the two lowest AWS sites. Precipitation occurs frequently at the coastal ice-shelf site, but in a more episodic fashion at the other sites. Precipitation has such large interannual variability that a 4year period is clearly too short for any conclusions to be drawn about seasonality. Surface sublimation exhibits much more regular seasonal behaviour, so a climatologically reliable description of these variables could be given.
Column drifting-snow sublimation was calculated using two different methods. In spite of the very different formulations, the methods generated similar cumulative drifting-snow sublimation fluxes. These fluxes are similar in magnitude to surface sublimation. However, the uncertainty in these estimates remains considerable, and more observations are needed to quantify the contribution of vertically integrated column drifting-snow sublimation to the surface mass balance of Antarctica.
In the summer period November-February, all ablation processes together remove 15-56% of the solid precipitation, or 6-27% on an annual basis. Intervals between precipitation events may last as long as several months, causing extensive summertime ablation.
Acknowledgements
We thank Institute for Marine and Atmospheric Research Utrecht personnel, participants in SWEDARP ’97/98 and personnel of the Alfred Wegener Institute, Germany, for setting up and maintaining the AWS. This work is partly funded by the Netherlands Antarctic Program (NAAP) and the Netherlands Organization of Scientific Research, Earth and Life Sciences section (NWO/ALW);it is also a contribution to the ‘European Project for Ice Coring in Antarctica’ (EPICA), a joint European Science Foundation (ESF)/European Commission (EC) scientific programme, funded by the EC and by national contributions from Belgium, Denmark, France, Germany, Italy, the Netherlands, Norway, Sweden, Switzerland and the United Kingdom. This is EPICA publication No. 123.



















