1. INTRODUCTION
Surface albedo is an important component of the global climate system due to its influence on Earth's radiation budget and energy balance. The snow-albedo feedback modifies climate through its impact on surface air temperatures and snow cover extent, and exerts a particularly strong influence in polar regions and regions of seasonal snow (Groisman and others, Reference Groisman, Karl and Knight1994; Pedersen and Winther, Reference Pedersen and Winther2005; Mote, Reference Mote2008; Flanner and others, Reference Flanner, Shell, Barlage, Perovich and Tschudi2011; Fletcher and others, Reference Fletcher, Zhao, Kushner and Fernandes2012). Recent trends of decreasing days with snow cover across the Northeast United States (Burakowski and others, Reference Burakowski, Wake, Braswell and Brown2008) and diminishing snow cover extent over the entire northern hemisphere during spring months (Lemke and others, Reference Lemke, Solomon, Qin, Manning, Chen, Marquis, Averyt, Tignor and Miller2007; Brown and Robinson, Reference Brown and Robinson2011; Estilow and others, Reference Estilow, Young and Robinson2015) are observed in synchrony with increasing wintertime and springtime air temperatures.
Quantifying the change of snow albedo on daily, seasonal and interannual timescales is critical for improving our understanding of the temporal variability in the surface energy balance and surface temperature (Burakowski and others, Reference Burakowski2016). In mid-latitude regions, snow cover follows a seasonal cycle as well as exhibiting interannual variability (Robock, Reference Robock1980). New snowfall events and snowpack evolution processes drive fluctuations in snow albedo on timescales of days, initiating changes in the amount of radiation absorbed by the surface (Warren and Wiscombe, Reference Warren and Wiscombe1980; Flanner and Zender, Reference Flanner and Zender2006). While the mechanisms controlling the increase in albedo following a fresh snowfall event are relatively straightforward, small-scale snowpack metamorphic processes that drive day-to-day albedo decay are more complicated and challenging to model accurately (Qu and Hall, Reference Qu and Hall2006).
Although theoretical relationships between snowpack evolution and albedo decay are well established (Warren and Wiscombe, Reference Warren and Wiscombe1980; Wiscombe and Warren, Reference Wiscombe and Warren1980; Warren, Reference Warren1982; Flanner and Zender, Reference Flanner and Zender2006), direct surface observations of snow albedo remain sparse or inconsistent, especially in areas of seasonal snow cover (van den Broeke and others, Reference van den Broeke, van As, Reijmer and van de Wal2004; Gardner and Sharp, Reference Gardner and Sharp2010). Here, we report on daily snow depth, density and surface albedo measurements collected across the state of New Hampshire by the Community Collaborative Rain, Hail and Snow-Albedo (CoCoRaHS-Albedo) volunteer science network (Burakowski and others, Reference Burakowski, Wake, Dibb and Stampone2013). The Community Collaborative Rain, Hail and Snow (CoCoRaHS) Network was established in 1998 in response to a 1997 flash flood in Fort Collins, Colorado, USA (Cifelli and others, Reference Cifelli2005). The network consists of over 7000 citizen scientist volunteers who collect daily rain, hail and/or snow observations using low-cost instrumentation in all 50 US states. CoCoRaHS data are used in a variety of research applications including weather forecasting (Schwartz, Reference Schwartz2014), drought monitoring (DeGaetano and others, Reference DeGaetano, Belcher and Noon2015), satellite verification (Sharma and others, Reference Sharma, Isik, Srivastava and Kalin2013; Sugg and others, Reference Sugg, Perry, Hall, Riggs and Badurek2014) and model validation (Hopper and Schumacher, Reference Hopper and Schumacher2012; Smith and others, Reference Smith, Smith, Baeck and Miller2015). In 2011, the CoCoRaHS-Albedo pilot project was launched to recruit CoCoRaHS observers to also collect daily snow albedo measurements (Burakowski and others, Reference Burakowski, Wake, Dibb and Stampone2013).
Among the sub-arctic research stations that measure albedo, most lack associated snow density and depth measurements (Table 1). The Surface Albedo Validation Sites (SAVS 1.0; Loew and others, Reference Loew2016) provides a one-stop clearinghouse for many of the sites in Table 1. However, it focuses on categorizing albedo sites by spatial and topographical heterogeneity and does not provide associated snow depth or density measurements. Within the Cryonet network, only five of the 32 sites are in sub-arctic regions and not situated on glaciers. There remains a dearth of in-situ albedo observations from spatially-distributed sites that can be used to investigate the factors controlling albedo changes in mid-latitude seasonal snowpacks. Here, the spatially and temporally dense observations from CoCoRaHS-Albedo measurements in New Hampshire over four winter seasons provide a unique opportunity to examine how albedo evolves with changing snowpack properties across an array of sites. The data we present are used to develop and test an empirical model to estimate albedo decay across the Northeast United States over periods of days via a suite of simple, readily available snowpack and atmospheric parameters.
Table 1. Inventory of research stations that collect in situ field measurements of snow albedo, density and depth (Y = yes, N = no)

* see globalcryospherewatch.org for list of sites and associated citations.
2. METHODS
Volunteer observers collected daily albedo, snow depth and snow density measurements across New Hampshire for four winter seasons (December 2011–April 2015; Table 2) using custom-designed snow sampling and albedo kits (Burakowski and others, Reference Burakowski, Wake, Dibb and Stampone2013). Concurrently, daily snow albedo, depth and density measurements were collected by University of New Hampshire (UNH) scientists at a site in Durham, New Hampshire. Due to a variety of reasons, the records from volunteer sites contain missing days. The ground surface at observation sites were mainly mowed lawns (lawn/athletic field) with the exceptions of sites NH-GR-11 (wooden observation deck), NH-MR-06, (bare soil) and NH-ST-99 (hay field mowed for harvest in late summer). Site elevations ranged from 20 to 545 m a.s.l. and proximity to the Atlantic Ocean coastline ranged from 7 to 147 km (Table 3). The spatial distribution of observation sites provides reasonable state-wide coverage (Fig. 1).

Fig. 1. Location of CoCoRAHS-Albedo measurement sites (black dots; primarily in New Hampshire, USA) and meteorological stations (blue triangles) that provided data used in this study.
Table 2. Time period and inventory of observers for snowpack measurements over four winters used in this study

Table 3. Summary information for all sites participating in the CoCoRAHS-Albedo network from 2011 to 2015

Sites in bold identify those that contributed data used in model calibration and evaluation.
a All stations except Windham, Maine (ME) are in the US state of New Hampshire (NH).
b All but the KPLY and CRREL sites are Global Historical Climatology Network stations.
The CoCoRaHS-Albedo kits were designed to be simple to use, yet capable of collecting scientifically useful data. An individual kit consists of a 2-foot (0.61 m) and a 4-foot (1.22 m) aluminum snow tube with internal diameter of 46 mm, a metal scraper, a hanging digital scale (CCi Model HS-6, CCi Scale Company, Clovis, CA), an Apogee MP-200 pyranometer (Apogee Instruments, Logan, UT) mounted onto a 0.91 m aluminum boom with circular bubble-levels and a field notebook. Each observer received a 1- to 2-hour training session by project personnel on how to correctly measure albedo, snow depth, snow density, maintain equipment and enter data online.
Snow depth (SD) measurements were obtained by vertically inserting the snow tube into the snowpack and recording depth to the nearest half inch (13 mm) according to the scale on the tube's side (field measurements use US customary units in alignment with national CoCoRaHS protocol). The tube bottom opening at the ground/snow interface was covered with the metal scraper before the tube was removed from the snowpack, and the bottom of the tube capped. The tube, cap and snow were weighed. The tare weight of the empty capped snow tube was subtracted from the total weight to yield the mass (M) of snow contained inside, which was then used to calculate snow density. Estimates of snow density include the following uncertainties: SD ±0.13 mm for the snow depth measurement (half from measurement scale on snow tube and half from potentially uneven ground surface); M± 0.2 g for the mass measurement; and a minimal error associated with the radius (r) of the tube, estimated at r ± 0.0.5 mm.
Albedo is defined as the ratio of upwelling (SW up ) to downwelling (SW down ) solar radiation:
Downwelling radiation was measured by positioning the Apogee MP-200 optic upwards in a horizontal manner; upwelling, or reflected radiation, was measured by inverting the optic to measure reflected radiation. The levels attached to both sides of the aluminum boom were used to ensure that the pyranometer was level for every measurement. Daily albedo values were calculated as the sum of three upwelling measurements divided by the sum of three downwelling paired radiation measurements using Eqn (1). Snow albedo is only weakly dependent on solar zenith angle (θ) when θ < 50o (Wiscombe and Warren, Reference Wiscombe and Warren1980), however since θ is >50o at the northernmost CoCoRaHS-Albedo sites during winter, albedo observations were taken within an hour of solar noon to minimize influence of solar zenith angle. Solar noon was determined for each site using the National Oceanic and Atmospheric Administration (NOAA) Solar Noon Calculator (http://www.esrl.noaa.gov/gmd/grad/solcalc/). Estimates of percent cloud cover were also recorded when the albedo measurements were made.
Volunteer observers began collecting albedo, snow depth and snow density measurements during late November or early December, depending on the date of first snowfall. They were instructed to take several snow-free albedo readings prior to the first snowfall event to test the equipment (for use in related land-cover albedo study) and for educational purposes to clearly demonstrate the difference in reflectivity between snow-free and snow-covered surfaces. Following spring snowmelt, volunteers again took several more snow-free albedo measurements at each sampling site. Snow-free measurements were also collected during mid-winter if melt events created bare ground between snow-covered periods. Recorded field observations for each day of sampling were entered into a digital data entry form on the CoCoRaHS-Albedo website (http://www.cocorahs-albedo.org/) along with general weather observations such as cloud cover, recent snowfall amounts, days since previous snow fall and melt events.
The Apogee MP-200 instrument measures total shortwave broadband (360 nm–1120 nm) albedo with an absolute accuracy of ±0.05, calibrated against a Kipp and Zonen CMA6 albedometer (Burakowski and others, Reference Burakowski, Wake, Dibb and Stampone2013). A spatial variability experiment was conducted in March 2014 consisting of 16 albedo measurement sites spaced 1.5 m apart in a 6 m × 6 m grid adjacent to the CoCoRaHS-Albedo observation site in Durham, NH. Albedo measurements were made with the Apogee MP-200 following CoCoRaHS-Albedo protocol for 5 consecutive days. Conditions were typical of early melt-season, with a snow depth of ~0.25 m, midday 2 m air temperatures close to 0°C, snow density near 350 kg m−3, surface albedo of ~0.75, and varying cloud cover between days. Under these circumstances, the coefficient of variation in surface albedo measurements among the 16 grid measurements ranged from 1 to 2%.
Maximum, minimum and daily average 2 m air temperatures were obtained from weather stations located closest to the albedo measurement site. Weather stations include Global Historical Climatology Network (GHCN) stations, a municipal airport weather station (KPLY) and the Cold Regions Research and Engineering Laboratory (CRREL) automatic weather station (Table 2). Most meteorological stations were not co-located with the CoCoRaHS-Albedo observation sites, but are all within 25 km, and 21 (of 27) are within 10 km (Fig. 1). Due to the relative proximity of the albedo and 2 m air temperature measurements, the 2 m air temperature records are assumed to be representative of conditions at the albedo measurement sites.
2.1 Albedo decay model development
To explore snow albedo decay over time, data from individual intervals of albedo decay were selected from the database of all CoCoRaHS-Albedo measurements. Decay intervals are defined by consecutive albedo decline lasting 4 or more days at a specific site, regardless of the month they occur or the starting albedo value. The threshold of 4 days represents a length of time long enough to capture fundamental processes of snowpack aging and albedo decline in our data but not so long as to severely limit the number of decay intervals available for analysis from our dataset.
We identify a total of 96 intervals of albedo decay lasting 4 or more days in length, including 12 from W1, 32 from W2, 30 from W3, and 22 from W4 (Table 2). By month, 11 occurred during December, 29 during January, 14 during February, 34 during March and 8 during April. Just over half of the decay periods (49 of 96) last only 4 days in duration while the other 47 range from 5 to 16 days.
Most of the measured albedo decay intervals begin immediately after a snowfall event; however, several begin a day or two after the end of the snowfall event. This delay may be due to small errors in albedo measurement associated with the time of measurement, changes in atmospheric or surface conditions (e.g. cloud cover, snow redistribution by the wind), or occasional missed albedo measurements. Of the 96 decay intervals used in model construction and validation, 64 begin within 1 day of a fresh snowfall and 80 begin within 3 days of a recorded snowfall event. Comparison of the rate of albedo reduction over time between decay intervals, which begin promptly following a snowfall and those which begin later reveals similar patterns of albedo decay.
Multiple linear regression models were constructed to estimate surface albedo values as a function of snowpack age, snowpack properties and 2 m air temperature statistics. Since the number of variables involved in a linear regression represents a trade-off between adding variables to improve prediction but limiting input variable redundancy, we first calculated pairwise linear correlations between albedo and candidate snowpack properties (daily depth, density and snow water equivalent (SWE)) and 2 m air temperature measures (daily minimum, maximum and average). The snowpack property and 2 m air temperature variables with strongest correlations to albedo were then used with snowpack age in the multiple linear regression models
The 96 albedo decay intervals were divided randomly into ‘calibration’ and ‘evaluation’ datasets using the random number function rand.m in Matlab R2014b. The calibration set was used to build the multiple linear regression models. The models were then tested on the evaluation dataset. To assess whether model performance was sensitive to calibration and evaluation data selection, a sensitivity analysis was conducted in which the 96 decay intervals were randomly sorted into two equivalent datasets over 10 iterations. Model performance statistics were gathered on each random iteration and used to determine the influence of data selection on model evaluation (Table 4).
Table 4. Summary statistics for model sensitivity to calibration and evaluation dataset selection

Multiple linear regression models constructed using calibration data were tested on evaluation data. Model performance was assessed via linear correlation coefficient (r), RMSE and slope of linear fit (m).
3. RESULTS
A total of 3249 individual daily albedo and snowpack measurements were collected by volunteer observers over the course of the four winter seasons at 27 different observer sites. Measured snow albedo exhibits significant day-to-day variability; the albedo record from Durham, NH for all four winter seasons provides an example of this variability (Fig. 2).

Fig. 2. Surface albedo measured in Durham, NH during (a) Winter 1 (December 2011–April 2012), (b) Winter 2 (2012/13), (c) Winter 3 (2013/14) and (d) Winter 4 (2014/15).
The 96 decay intervals (497 total measurements) show considerable variability in the rate of surface albedo decline over time (Fig. 3). Within the first day following peak albedo, albedo reductions range from 0.01 to 0.25. After the first 2 days, albedo values decline by 0.01 to 0.32 and after three days, albedo reductions range from 0.03 to 0.47.

Fig. 3. Albedo decay events plotted as an albedo anomaly calculated from Day 0. Each line represents a single albedo decay event.
Baker and others (Reference Baker, Skaggs and Ruschy1991) quantify the snow depth above which the snowpack is considered to be optically thick and whereupon the underlying terrain is effectively masked. Our data show that albedo increases rapidly with snow depth up to ~0.14 m. Further deepening of the snow up to ~0.50 m does not result in a corresponding increase in albedo (Fig. 4). A modest increase in albedo is apparent as SD increase from 0.5 to 0.8 m. A snow depth threshold of 0.14 m is subsequently used to divide the 96 decay intervals into shallow (SD < 0.14 m; ‘non-optically thick’) snow and deep (SD > 0.14 m; ‘optically thick’) snow regimes.

Fig. 4. Snow albedo versus snow depth using data from all decay events from all four winter seasons (2011–15). Station IDs are listed in Table 3. The black line is a LOWESS (locally weighted regression scatterplot smoothing) curve which enables the visibility of trends otherwise obscured by data scatter and outliers. Albedo values are interpreted to plateau beginning at ~0.14 m snow depth (identified by the dashed vertical line).
Snow albedo for both shallow and deep snowpacks showed high negative correlations with snow age and daily average 2 m temperature (Fig. 5). Shallow snowpacks show the highest (positive) correlation with daily snow depth, while deeper snowpacks show strongest (negative) correlation with daily snow density. Surprisingly, daily SWE was not highly correlated with albedo in either shallow or deep snowpacks.

Fig. 5. Linear correlations (r) between observed albedo and time (days), snowpack and weather variables during times of albedo decay for calibration dataset; (a) snowpacks SD < 0.14 m and (b) snowpacks SD > 0.14 cm displayed. Gray bars represent the time category and includes the snow age variable; blue bars represent the snowpack category and include snow depth, snow density and snow water equivalent (SWE) variables; and red bars represent meteorological parameters which include minimum, average, and maximum daily temperature and daily temperature range.
3.1 Multiple linear regression
Based on the results shown in Figure 5, snow age (τ in days), average daily 2 m air temperature (T in °C), and daily snow depth (SD in m) for shallow snowpacks and daily snow density (ρ in kg m−3) for deep snowpacks, were selected for use in our multiple linear regression analysis. Multiple linear regression models were constructed for both groups using ten randomly generated calibration and evaluation datasets (Table 4). A test of the 95% confidence intervals for the slope of each model's goodness of fit statistics revealed no significant trends over the course of the ten sensitivity runs. Given the absence of significant correlation between calibration and evaluation dataset selection and model performance, we report the details from the first of the ten calibration and evaluation datasets as being sufficiently representative of the modeling analysis results. The regression equation for shallow snowpacks (SD < 0.14 m) is expressed as:
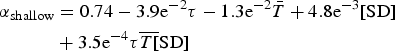 $$\eqalign{\alpha _{{\rm shallow}} & = 0.74 - 3.9{\rm e}^{ - 2}\tau - 1.3{\rm e}^{ - 2}\bar T + 4.8{\rm e}^{ - 3}[{\rm SD}] \cr & + 3.5{\rm e}^{ - 4} {\tau} \overline {T[} {\rm SD}]}$$
$$\eqalign{\alpha _{{\rm shallow}} & = 0.74 - 3.9{\rm e}^{ - 2}\tau - 1.3{\rm e}^{ - 2}\bar T + 4.8{\rm e}^{ - 3}[{\rm SD}] \cr & + 3.5{\rm e}^{ - 4} {\tau} \overline {T[} {\rm SD}]}$$
where α shallow is the predicted albedo value. The regression equation for surface albedo (α deep) in deep snowpacks (SD > 0.14 m) is expressed as:
The multiple linear regression models are first evaluated on their ability to estimate measured albedo values in the same calibration dataset from which Eqns (2) and (3) were constructed. Modeled albedo from the shallow snowpacks regression show a strong linear correlation with observed albedo, with an r value of 0.75, RMSE of 0.10, and slope (calculated using a least-squares fit) of 0.56 (Fig. 6a). The model estimates values of albedo ranging from 0.35 to 0.94. Modeled albedo values for deep snowpacks (SD > 0.14 m) also show a strong linear relationship (r = 0.72; RMS = 0.10, and a slope of 0.55) over a wide range of albedo (Fig. 6b).

Fig. 6. Albedo values modeled from multiple linear regression using snow age, air temperature and snow properties (snow depth for shallow snowpacks, snow density for deep snowpacks) compared with calibration data for (a) shallow and (b) deep snowpacks. Model skill is assessed using linear correlation (r), RMSE, and slope (m) for both shallow and deep snow covers. N value denotes number of individual measurements on plot. The solid black line represents the least-squares regression line; the dashed grey line is the 1:1 line.
The multiple linear regression models were then tested against the evaluation dataset to determine their ability to estimate albedo decay over time. Snow age, snowpack property (SD for shallow snowpacks; ρ for deep snowpacks), and T for each decay interval in the evaluation dataset were input into the models to estimate albedo, and the results compared with measured values (Fig. 7). The shallow snow model predicts 111 albedo values ranging from 0.40 to 0.94 with an r value of 0.70 and an RMSE of 0.10 (Fig. 7a). Compared with the 1:1 reference line, the scatter of data trend towards over-estimation of low albedo values and under-estimation of high values, also signified by the slope value of 0.57 (similar to results using the calibration dataset in Fig. 6). The deep snow model predicts 116 albedo values from 0.52 to 0.96 with an r value of 0.74, an RMSE of 0.07 and a slope of 0.49 (Fig. 7b). In comparison with the 1:1 reference line, low albedo values are again overestimated while high values are generally underestimated.

Fig. 7. Albedo values modeled from multiple linear regression using snow age, air temperature and snow properties (snow depth for shallow snowpacks, snow density for deep snowpacks) compared to evaluation data for (a) shallow and (b) deep snowpacks. Model skill is assessed using linear correlation (r), RMSE and slope (m) for both shallow and deep snow covers. N value denotes number of individual measurements on plot. The solid black line represents the least-squares regression line; the dashed grey line is the 1:1 line.
Model bias is estimated by calculating the residuals (modeled – observed). The residuals of the multiple linear regression models are plotted against surface albedo and exhibit a clear negative trend for both shallow and deep snowpacks (Fig. 8). In shallow snow, the regression model generally over-estimates albedo <0.63, and under-estimates albedo >0.63 (Fig. 8a). Despite this bias, 70% (78 of 111) of modeled albedo values are estimated to within 0.1 of measured albedo while 96% of modeled values are within 0.2. In deep snow, albedo is generally over-estimated below 0.78 and under-estimated above 0.78 (Fig. 8b). Ninety percent (104 of 116) of modeled albedo values in deep snowpacks are within 0.1 of measured values, and all are within 0.2.

Fig. 8. Residuals (modeled minus observed albedo) plotted against albedo for (a) shallow and (b) deep snowpacks. Both shallow and deep snowpack models over-estimate low albedo and under-estimate high albedo. The solid black sloping line represents the least-squares regression line.
4. DISCUSSION
The CoCoRaHS-Albedo data exhibit characteristic albedo reduction with increasing snowpack age, consistent with other mid-latitude albedo observations (Pedersen and Winther, Reference Pedersen and Winther2005; Chen and others, Reference Chen, Weiping, Weijing and Xin2014; Malik and others, Reference Malik, van der Velde, Vekerdy and Su2014; Adolph and others, Reference Adolph2016) as well as theoretical understanding of albedo evolution (Warren and Wiscombe, Reference Warren and Wiscombe1980; Flanner and Zender, Reference Flanner and Zender2006). The results show that large amount of data collected by volunteer observers in the CoCoRaHS-Albedo network are useful for investigating the behavior of surface albedo in seasonal snowpacks.
Trends in surface snow albedo decay over time are analyzed separately in optically deep and optically shallow snowpacks. The surface albedo of optically shallow snow is influenced by the substrate albedo in addition to snow properties, whereas the albedo of optically deep snow depends solely on optical snow parameters. The snow depth marking the transition between optically shallow and optically deep snow is a function of wavelength (Wiscombe and Warren, Reference Wiscombe and Warren1980) and varies considerably depending on snow grain size and density in multilayer radiative transfer models (Zhou and others, Reference Zhou, Li and Stamnes2003). For seasonal snowpacks across New Hampshire over four winter seasons, analysis of hundreds of snow albedo measurements at dozens of sites (Table 3) indicates that the optical snow depth threshold occurs at ~0.14 m snow depth (Fig. 4). This depth of 0.14 m is near the upper end of the range of 0.075 to 0.15 m identified by Baker and others (Reference Baker, Skaggs and Ruschy1991) over surface types varying from bare soil to alfalfa, and slightly more than the value of 0.10 m, which is generally considered an optical threshold depth in surface energy-balance studies (Winther, Reference Winther1993; Pedersen and Winther, Reference Pedersen and Winther2005; Perovich, Reference Perovich2007; Mote, Reference Mote2008; Tanikawa and others, Reference Tanikawa2009; Aoki and others, Reference Aoki2011).
Optically shallow snowpacks (SD < 0.14 m) in New Hampshire occur predominantly at the beginning and end of the snow season and occasionally during mid-winter thaws. The albedo decay process of optically shallow snowpacks is more complex compared with deeper snowpacks due to the additional influence of underlying terrain, and accurately parameterizing albedo evolution in shallow snow presents a challenge (Slater and others, Reference Slater, Pitman and Desborough1998). Both shallow and deep snowpacks are subject to surface albedo degradation via snow metamorphism and particulate accumulation. However, albedo reduction of thin snow cover accelerates when solar radiation penetrates through the snow pack and the lower albedo of the underlying substrate increases absorption of solar radiation. As snow cover decreases, surface albedo approaches that of the substrate until snow cover disappears altogether (Gray and Landine, Reference Gray and Landine1987). Additionally, the presence of adjacent bare ground further accelerates snow melt where snow remains. In the CoCoRaHS-Albedo dataset, correlation between snow depth and surface albedo for shallow snowpacks implies snow depth represents some of the complex influences on snow surface albedo brought about by visible ground beneath the snowpack and adjacent bare ground. In addition, the large scatter and lower albedo values (albedo <0.45) in the residuals plot for shallow snowpacks (Fig. 8a) are indicative of the influence of the underlying substrate.
In optically deep snowpacks (SD > 0.14 m), both theoretical and empirical studies show that snow surface albedo declines principally in response to complex metamorphosis within the snowpack that increase optical grain size and concentration of impurities (Warren and Wiscombe, Reference Warren and Wiscombe1980, Wiscombe and Warren, Reference Wiscombe and Warren1980; Warren, Reference Warren1982; Aoki and others, Reference Aoki2000, Reference Aoki, Hachikubo and Hori2003; Cabanes and others, Reference Cabanes, Legagneux and Domine2002; Flanner and Zender, Reference Flanner and Zender2006; Domine and others, Reference Domine2008). At air temperatures higher than 0 °C, the presence of liquid water within the snow matrix enhances grain growth, further reducing albedo (Colbeck, Reference Colbeck1982; Flanner and Zender, Reference Flanner and Zender2006) and increasing snow density. Surface albedo can also be reduced via accumulation of particles, including black carbon (BC), on the snow surface (Warren and Wiscombe, Reference Warren and Wiscombe1980; Flanner and others, Reference Flanner, Zender, Randerson and Rasch2007; Doherty and others, Reference Doherty2013). However, recent measurement and analysis of albedo and BC at three open sites across New Hampshire over three winter seasons have shown that BC has a minimal effect on albedo compared with optical grain size of the surface snow (Adolph and others, Reference Adolph2016).
While acknowledging these complexities, we have attempted to develop simple linear models to estimate albedo decay in snowpacks based solely on snow age, snowpack properties (depth or density), and 2 m air temperature; all of which are assumed to be proxy variables for changes in microphysical snowpack properties, such as grain growth and impurity loading. Our approach incorporates easily replicable, low cost data collection methods and analysis. Calibration and evaluation of multiple linear regression Eqns (2) and (3) in the context of quantifying snow albedo decay behavior confirm strong relationships among snow surface albedo values, snowpack age and 2 m air temperature, which are commonly available in climate model routines. Snow age and 2 m air temperature are found to be important determinants of surface albedo for both shallow and deep snow covers; however, addition of simple snowpack measures enhances the estimation of albedo in both snow cover types. For snowpacks with SD < 0.14 m deep, albedo is more strongly correlated with snow depth than snow density, indicative of the contribution of underlying terrain to snow surface albedo as well as the influence of adjacent snow cover fraction. For snowpacks with SD > 0.14 m in depth, albedo is more strongly correlated with snow density than snow depth, likely owing to its surrogate connection with snow grain evolution processes and liquid water content.
In Table 5 we report the skill of our deep snowpack model in comparison with similar albedo schemes developed by Verseghy (Reference Verseghy1991); Douville and others (Reference Douville, Royer and Mahfouf1995) and Adolph and others (Reference Adolph2016). It is acknowledged that these models calculate albedo solely as functions of snow age and air temperature. The intent of our comparison is not to determine the best parameterization but rather to understand the strengths and deficiencies of simple albedo modeling approaches. Verseghy (Reference Verseghy1991) and Douville and others (Reference Douville, Royer and Mahfouf1995) both employ exponential prognostic equations for albedo decay dependent on snow age and air temperature. Adolph and others (Reference Adolph2016) present a linear regression model using snow age and mean air temperature to compute albedo decay of snow at a single NH site over three of the four winter seasons studied here. Although the three other models use 0.10 m as an optical threshold and thus were developed for use on snowpacks exceeding this depth, we tested all models using snowpacks deeper than 0.14 m since we observed this depth to be the optical threshold for snowpacks in NH.
Table 5. Summary statistics for albedo decay models tested on CoCoRAHS-Albedo evaluation data for optically thick snowpacks (SD > 0.14 m)

The models from the literature exhibit similar skill to one another when tested against 116 daily deep snowpack CoCoRaHS-Albedo observations, with linear correlation factors of 0.55–0.56 and slopes of 0.28–0.46. The model presented in this paper has both a higher r value (0.74) and slope (0.49) than the other three, but this is unsurprising considering it was developed using CoCoRaHS-Albedo data. All four models accurately compute albedo values from 0.7 to 0.8 but diminish in capability outside of this range, regardless of whether decay is represented as a linear or exponential process. The three models from the literature struggle with under-estimation of high albedo values and over-estimation of low albedo values to a greater degree than our model does, as illustrated by slope values all <0.5 (Table 5). A portion of this variability may be explained by the fresh snow reset values of 0.84 (Douville and others, Reference Douville, Royer and Mahfouf1995) and 0.85 (Verseghy, Reference Verseghy1991), which represent albedo maxima for their respective models; these albedo values are less than a substantial number (24%) of measured albedo values in the CoCoRaHS-Albedo deep snow evaluation dataset.
Despite the encouraging performance of the two multiple linear regression models developed in this study, systematic biases highlight an important non-linearity in albedo decay and snowpack evolution. Modeled albedo values are reasonably accurate within the range of 0.6–0.9, but exhibit a tendency to over-estimate lower albedo values and under-estimate higher albedo values. We hypothesize that this characteristic of all the linear models is due to the dominance of slow metamorphic evolution of snow grains through most of the winter season. Fresh snow, with highest albedo, experiences more rapid changes as vapor transfer leads to rounding of microstructures and decrease in the snow specific surface area (Cabanes and others, Reference Cabanes, Legagneux and Domine2002; Domine and others, Reference Domine2008). Later in the season and during mid-winter melt events, the presence of liquid water in the snowpack results in accelerated metamorphism and grain growth (Colbeck, Reference Colbeck1982). Simple models assuming constant rates of grain evolution are unable to capture these important intervals of faster evolution.
5. CONCLUSIONS
Quantifying the variability of snow albedo via direct observations is critical for accurate representation of surface energy balance in numerical models. Over the course of four consecutive winter seasons CoCoRaHS-Albedo volunteers collected 3249 daily albedo and snowpack measurements from sites across New Hampshire, amassing an observational dataset that, to our knowledge, represents the densest array of ground-based albedo measurements in a temperate seasonal snowpack. Analysis of the spatially robust dataset demonstrates the optical snow depth threshold value to be ~0.14 m snow depth.
Simple multiple linear regression models using snowpack age, snow depth or snow density and 2 m air temperature provide reasonable estimates of surface snow albedo during times of albedo decay at sites across New Hampshire for both shallow (SD < 0.14 m) and deep (SD > 0.14 m) snowpacks. Despite strong correlation with observed values, estimated albedo exhibit a tendency to overestimate low albedo values and underestimate high albedo, suggesting our set of predictor variables may best model albedo reduction over a limited range of linear response (0.6–0.9). We hypothesize that more rapid changes in albedo in fresh snow (albedo >0.9) are the result of vapor transfer causing rounding of microstructures and a decrease in the snow specific surface area, while during melt-events the presence of liquid water in the snowpack (albedo <0.6) accelerates metamorphism and rapid grain growth results.
The CoCoRaHS-Albedo network represents an albedo measurement campaign that relies upon volunteer observers to provide a dense array of snow albedo observation at dozens of sites across New Hampshire. Weather-enthusiasts, primary and secondary school educators, students and university researchers alike contributed scientifically-useful observational data from dispersed locations, successfully providing data suitable for climate model validation (Burakowski and others, Reference Burakowski, Wake, Dibb and Stampone2013) and empirical albedo decay modeling. Although volunteer observers ultimately provided the bulk of suitable measurements, engagement with primary and secondary school educators has fostered many local scientific outreach opportunities, including a high school snow sampling lesson plan that meets Next Generation Science Standards (Hanson and Burakowski, Reference Hanson and Burakowski2015). We conclude that the CoCoRaHS-Albedo volunteer observer network provides useful snow albedo, depth and density measurements and serves as an effective model for future measurement campaigns.
ACKNOWLEDGEMENTS
We thank all of the volunteer observers in the CoCoRaHS-Albedo Network for their contributions to this study. This work was supported by the New Hampshire EPSCoR Program with funding provided by the National Science Foundation's Research Infrastructure Improvement Award EPS 1101245. Data collected throughout the NH EPSCoR Track 1 project, including data leading to relevant conclusions in this work, can be found on the Data Discovery Center at http://ddc-albedo.sr.unh.edu. We also appreciate the reviewer comments and helpful critiques on earlier drafts of this manuscript.















