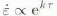Introduction
It has been known for some time that glaciers could deform granular materials which they over-rode (e.g. Reference MacClintock, and DreimanisMacClintock and Dreimanis, 1964). Widespread interest in the rheology of such materials, however, dates from 1986 at which time it was realized that Ice Stream B in Antarctica probably rested on a layer of till which was inferred to be deforming rapidly, and to which the ice stream owed its high speed despite the low driving stress (Reference Blankenship,, Bentley, Rooney and AlleyBlankenship and others, 1986; Reference Alley,, Blankenship, R and RooneyAlley and others, 1987a, Reference Alley,, Blankenship, Roony and Bentleyb). Of concern is the possibility that, should the Antarctic ice shelves disintegrate as a consequence of rising sea level, rapid flow of ice streams on such materials might lead to collapse of the West Antarctic ice sheet (Reference Mercer,Mercer, 1978). As much of the ice sheet is above sea level, such a collapse could raise sea level rapidly enough to be disruptive to human activities in coastal areas.
More recently, it has been suggested that sediment transfer in such deforming till layers might be geomorphologically significant. Reference Alley,Alley (1991) proposed that the vast till sheets of the mid-continent region of the United States might have been emplaced by this mechanism, and Reference Hooke, and Elverhøi.Hooke and Elverhøi (1996) thought that transfer of sediment from a fjord on Spitsbergen to a huge fan on the continental slope could only have occurred in this way.
In addition, it has long been suspected that some ice lobes in the mid-continent area of North America may have had quite low surface slopes and thicknesses, and hence almost unbelievably low driving stresses (Reference Mathews,Mathews, 1974; Reference Clark,Clark, 1992). The ice transfer needed to form and possibly to maintain such lobes could only have occurred if they were able to flow rapidly despite the low driving stress. It is now widely believed that this rapid flow was possible because the lobes rested on layers of deforming till, and that it may have occurred in a non-steady-state (surge) mode.
Previous Work
The resulting interest in modelling these processes has led to a search for a constitutive relation between stress, τ, and strain rate,

(Reference Boulton, and Hindmarsh.Boulton and Hindmarsh, 1987). Here, τ c is a critical stress below which no permanent deformation occurs, P c is the effective pressure (overburden pressure minus pore-water pressure) and n and m are empirical constants, τc is usually taken to be the Mohr – Coulomb strength:
where c is the cohesion and φ is the angle of internal friction. Reference Boulton, and Hindmarsh.Boulton and Hindmarsh (1987) measured deformation rates in till beneath the margin of Breiðamerkurjökull in Iceland and obtained simultaneous records of pore-water pressure. They also reported shear stresses but did not explain how they were obtained. The reported shear stresses vary more than is physically likely, as the geometry of the experiment suggests that τ was probably dominated by longitudinal stress gradients rather than, for example, by thickness and surface slope. Thus, there are no reliable experimental data in support of a relation of the form of Equation (1).
Engineers have long been interested in the rheology of granular materials for quite different reasons. Studies of failure of previously sheared materials, such as slow-moving landslides, have led to the realization that the strength of a previously consolidated granular material, deformed at a steady rate in shear, will rise quickly to a peak value and then decline, sometimes by as much as 75% from the peak value (Reference Bishop,, Green, Garga, Andersen and BrownBishop and others, 1971; Reference Skempton,Skempton, 1985). The final value attained is called the residual strength, τr. Thus, from the point of view of continuous till deformation, as Reference Kamb,Kamb (1991) has noted, we are interested in the stress-dependence of the residual strength. That is, we wish to know whether the residual strength of the material increases with the rate of deformation and, if so, how rapidly. At a deeper level of understanding, we would like to know, mechanically, why it varies in this way.
Laboratory studies have shown that the residual strength does increase with strain rate, but not much. The experimental results are described by an equation of the form:

(Reference Mitchell,Mitchell, 1993, fig. 14, 15). Here, τ 0 is the stress at a reference strain rate
Equation (3) may be written, taking τr = τ as the independent variable:

where k = 1/b and β = e−k. Based on the experimental values of b, ∼ 10 < k < ∼ 60. Because τ > τ 0, such a constitutive relation implies that strain rates should increase substantially with only a small increase in τ, as Reference Kamb,Kamb (1991) recognized.
P e does not appear explicitly in Equation (4) but, since τ must be greater than τ c (Equation (3)), let us say by an amount Δτ, we can write:
Δτ will depend upon the choice of ![]() and τ
0 but, as a first approximation, we assume that it is independent of P
e. This, however, needs to be tested as P
e was not varied in the experiments upon which Equation (3) is based.
and τ
0 but, as a first approximation, we assume that it is independent of P
e. This, however, needs to be tested as P
e was not varied in the experiments upon which Equation (3) is based.
Instrumentation
To study the rheology of deforming till in the field, we initiated a study on Storglaciären, a small valley glacier in northern Sweden. A summary of previous work on the glacier can be found in Reference Hooke,, Pohjola, Jansson and KohlerHooke and others (1992) and the references cited therein. The measurements we made included surface velocity, water pressure, minimum till thickness, and both strain rate and strength in the sub-glacial till. For the latter measurements, holes were drilled through the glacier with the use of a hot-water drill, instruments were emplaced in the till through the holes, and data were recorded on Campbell CR-10 data loggers. The ice was ∼95 m thick at the site of the experiments conducted in 1992 and 1993, and ∼125 m thick at the site of the 1994 and 1995 work.
Drilling and instrument insertion were done during the month of July every year. Initially, data collection was terminated in early August but more recently we have arranged to have someone stay in the field until late August to continue to service the distance meters, a daily task, and have kept the loggers operating into the fall and winter.
Brief descriptions of the techniques follow.
Surface Velocity
The speed of a stake drilled into the surface of the glacier near the site of the till experiments was measured, effectively continuously, using a computer-controlled electronic distance meter (EDM). At 10 min intervals, the EDM measured the distance between the stake and a fixed point off the glacier, toward which the stake was moving. The instrument set-up and procedure used for reducing the distance measurements to speeds have been described by Reference Hanson, and HookeHanson and Hooke (1994). These EDM measurements were supplemented by surveys with an electronic theodolite on a daily to weekly basis, as permitted by weather, to provide three-dimensional velocities over the season.
During the 1995 held season, a strain net consisting of six additional stakes distributed around the site was also surveyed With the electronic theodolite. The resulting data were used in a force-balance calculation, following procedures outlined by Reference Van der Veen, and WhillansVan der Veen and Whillans 1989. Vertical derivatives of horizontal velocities were estimated using the simple assumption that 20% of the surface velocity was caused by internal deformation. For each triangle radiating from the central stake, strain-rate tensors were constructed by direct linear fitting, and stress gradients across this set of triangles were calculated by least-squares fitting of a planar trend surface.
The calculated forces correspond to a driving stress of 75 k Pa, enhanced by a 6 k Pa longitudinal stress but resisted by a 40 k Pa side drag, resulting in a mean net basal drag of 41 k pa. These values were not particularly sensitive to assumptions regarding vertical derivatives or to decisions about which stakes should be included in the analysis.
Water Pressure
Local water pressures were measured with the use of pressure transducers submerged in boreholes. Pressure transducers in nearby boreholes tracked each other so closely that pressures in all boreholes can be considered uniform. We believe that this is because the holes are connected by a network of englacial conduits (Reference Hooke, and PohjolaHooke and Pohjola, 1994). In 1995, we also inserted a pressure transducer in the subglacial till. Results of this experiment will be discussed later.
Till Thickness
The minimum till thickness was measured with the use of a penetrometer, a pointed, hardened steel rod that could be pounded into the till by raising and releasing a weight suspended on a cable. The weight could be raised about 0.5 m. When released, it slid down along the rod, impacting on a collar welded ∼0.5 m above the point.
With the exception of a few very low readings, we were consistently able to drive the penetrometer between 0.2 and 0.35 m. The mean maximum penetration was ∼0.3 m. However, we have no way of knowing whether penetration ceased because the penetrometer encountered till that was too compact to penetrate, a rock in the till, or bedrock.
Strain Rates in the Till
Shear strain rates were measured with the use of dual-axis leaf-spring tiltmeters inserted into the till. The tiltmeters and insertion techniques were modelled after those of Reference Blake,, Clarke and Gérin.Blake and others (1992). The tiltmeters were 85 mm long in 1992 and 1993, and 50 mm long in 1994 and 1995. They were typically driven into the till 0.15 – 0.2 m. However, there is always uncertainty about the precise position of the instrument. For the first few days following insertion, tiltmeters commonly did not behave in a manner consistent with being firmly embedded in the till. Furthermore, by the time they began to yield believable data they were typically tilted from the vertical, sometimes by as much as 30 °. In some cases, the tiltmeters may have been inserted into till squeezed upward into the bottom of a borehole, or alternatively into a sub-glacial layer softened by the hot-water drill — it is impossible to know exactly what is happening at the bottom of a 100 m hole.
Once a tiltmeter appeared to be yielding reliable data, the calculation of till rates in the till (e.g. Fig. 1) was still complicated by the fact that we do not know the initial orientation of the tiltmeter. Pole positions of the tiltmeter were rotated into a coordinate system in which the direction of the maximum tilt rate could be determined and this maximum tilt rate is that plotted in our figures; we assume that it is in the down-glacier direction. Reduction of these (often noisy) data to first derivatives was accomplished either by applying a running first-derivative filter to the record (Reference Abramowitz, and StegunAbramowitz and Stegun, 1965, p. 914) followed by taking a running mean (1992 and 1993), or by using an error-correcting spline routine (1994 and 1995).

Fig. 1. Time series of: (a) surface speed, tilt rate and drag from July 1992; and (b) surface speed, till rate and effective pressure from July – August 1993. In both records, the large peaks in us were associated with rain storms
Till Strength
Till strength was measured with two devices, dragometers, or draggers for short, and ploughmeters. Detailed descriptions of these instruments have been given by Reference Iverson,, Jansson and HookeIverson and others (1994) and Reference Fischer, and Clarke.Fischer and Clarke (1994), respectively. Briefly, a dragger consists of a cylinder, the “fish”, that is pulled through the till by a wire. The fish is 100 mm long and 19 mm in diameter, and has conical ends. The wire passes upward through a 1.9 m long steel tube in the bottom of the borehole and is attached to a load cell at the upper end of the tube. The base of the tube is embedded in the till to a depth which was thought to be ∼0.1 – 0.2 m but which, as explained above, is effectively unknown.
Ploughmeters are steel rods, ∼1.5 in long, to which strain gauges have been bonded. The rods are driven ∼0.1 – 0.2 m into the till and are then dragged through the till as the glacier moves. Elastic bending of the rods is recorded by the strain gauges and is converted into a force on the rod with the use of a laboratory calibration. Ploughmeters were deployed only in 1995.
Till Composition
Samples of till were retrieved through boreholes with the use of a sampler consisting of a tube with a closed, pointed end. Till entered the tube through a ∼10 mm wide slot in the side. A sleeve slid down over the slot as the sampler was withdrawn. This inhibited but did not completely prevent loss of fines as the sampler was raised through the water column. Data on the size distribution of the till and on some of its other properties are summarized in Table 1.
Table.1. Properties of Storglaciären till

Murphy
As might be expected, but as can only be fully appreciated by those who have tried such experiments, Murphy’s law prevailed during these experiments. Problems with knowing the depth to which instruments were inserted have already been described. More frustrating are those instruments which appear to have been inserted flawlessly but which never return comprehensible data. In addition to such instrumental problems, we are also dependent upon the glacier to do something interesting during the time the instruments are working. We obviously have no control over this variable, which is probably just as well.
Suffice it to say that despite 5 years of effort, we have, on only a few occasions, obtained interpretable time series from several instruments simultaneously. This paper and a previous one (Reference Iverson,, Hanson, Hooke and JanssenIverson and others, 1995) focus on these records.
Results
Some early results of these studies have been published previously (Reference Iverson,, Hanson, Hooke and JanssenIverson and others, 1995). In that paper, we focused on records during major storms to which the glacier reacted strongly (Fig. 1), although a good record of diurnal variations was also obtained (Fig. 1b). During storms, the glacier speeds up but strain rates in the till and the force on the dragger both decrease. This led us to conclude that increased water pressures (reduced P1 ) weaken the coupling between the glacier and the till, allowing the glacier to move over the till faster while deforming it less rapidly. In addition, we inferred that elevated water pressures weaken the till (Equation (2)), resulting in less force on the dragger. (Water pressures were not obtained during the time series in Figure 1a owing to failure of Rustrak data loggers that persistently misbehaved under humid conditions. However, surface velocity and water pressure typically vary in phase during major events (Fig. 1b).)
New results discussed here are presented in Figures 2 – 5. Figure 2 shows an 11 d segment of a time series that extends from late July through to late September. During this 11 d period, water pressure and tilt rate varied diurnally. The dragger record also has a diurnal signal which is in phase with the other records but this has been suppressed by starting the ordinate scale at 0 in order to emphasize the lack of variation rather than to bring out the small variations that do exist.

Fig. 2. Time series of drag, effective pressure and tilt rate from August 1994
To underscore the consistency of the relations among the records in Figure 2, the daily cycles for 18 – 28 August have been stacked (Fig. 3). To stack the records, we averaged values of each variable at the same time each day, in 0.01 d (∼15 min) intervals, starting at midnight. (As the maxima occurred at close to the same time every day, a stacking based on the time of one of the maxima rather than on midnight would not differ significantly from that shown in Figure 3. For example, the maxima in P e occurred at 0840 h on 5 of the 10 d and at 0755, 0855, 0910 and 0935 h on the other 5 d. Such small differences are not resolvable with a 0.01 d gridding.) In the dragger record, the gradual increase with time observable in Figure 2 was removed (assuming linearity) before stacking, and the ordinate was expanded to emphasize the diurnal signal.

Fig. 3. Stacked time series of drag, effective pressure and tilt rate from 18 to 28 August 1994, and of surface velocity from 6 to 12 August 1994. Stacking procedures for incorporating the us record are described in the text.
Surface-velocity measurements were terminated ![]() before the beginning of the segment of record shown in Figure 2. However, the diurnal velocity and till records from 6 to 12 August displayed a consistent phase relation. Stacked records from this 6 d period showed a maximum in till at 0740 h, 20 min after the tilt maximum shown in Figure 3. We have, therefore, plotted in Figure 3 the stacked surface-speed record from 6 to 12 August, shifted backwards 20 min, in order to give an idea of how the surface speed may have varied between 18 and 28 August.
before the beginning of the segment of record shown in Figure 2. However, the diurnal velocity and till records from 6 to 12 August displayed a consistent phase relation. Stacked records from this 6 d period showed a maximum in till at 0740 h, 20 min after the tilt maximum shown in Figure 3. We have, therefore, plotted in Figure 3 the stacked surface-speed record from 6 to 12 August, shifted backwards 20 min, in order to give an idea of how the surface speed may have varied between 18 and 28 August.
In Figures 4 and 5, we present, respectively, a 60 d record of effective pressure, surface speed, and force on the ploughmeter; and the pressure record in a borehole together with the difference between the pressure in the till and that in the hole.

Fig. 4. Time series of effective pressure, surface speed and force on the ploughmeter from 1995. Brief periods of negative effective pressure are believed to be real but they may be due to errors in the measurement of ice thickness or depth to the transducer

Fig. 5. Water pressure in a borehole and difference between pressure in the borehole and that in the underlying till. Record starts about 50 d after emplacement of the transducer in the till. Pressure in the till is generally higher than that in the borehole over the time span shown.
Sliding Speed
It would be useful to know the temporal variation in the speed, u b, with which the base of the glacier moves relative to either the top of the till layer or the underlying bedrock. Our early attempts to measure u b Utilized “slidometers” of our own design, whereas in 1995 we employed a design used successfully elsewhere (Reference Blake,, Clarke and Gérin.Blake and others, 1992). Despite these efforts, Murphy took control and no useful results were obtained.
In the absence of direct measurements of u b, we rely on indirect calculations and assumptions. Borehole-deformation measurements in 1988 – 89 in a borehole ∼300m up-glacier from the site of the present experiment yielded u s − u b = 10 mm d−1 (Reference Hooke,, Pohjola, Jansson and KohlerHooke and others, 1992). We used this to estimate the ratio S f/B in the relation:

(Reference Nye,Nye, 1952, р. 86) where S f is a shape factor, ρ is the density of ice, g is the acceleration due to gravity, H is the glacier thickness, α is the surface slope, and β is a viscosity parameter. Using this value of S f/B and appropriate values of H and α, we calculate that at the site of the experiment u s − u b ≈ 6 mm d−1. As mean summer surface speeds are in the 45 – 50 mm d−1 range, this implies a mean u b of ∼40 mm d−1.
Because ice is a crystalline material with properties that should remain reasonably constant over the time periods considered here, we infer that measured variations in surface speed reflect, primarily, variations in u b. Indeed, with the use of a video camera, we have observed changes in u b in nearby boreholes on a time-scale of hours (Reference Pohjola,Pohjola, 1993). More recent work with a different video system yielded a discontinuous record of u b (Fig. 6) and also suggested that changes in surface velocity reflect, primarily, changes in u b.

Fig. 6. Surface speed, effective pressure and sliding speed during several days in July 1991. Sliding speed was measured with a video camera suspended in a borehole just above the till bed. The record is discontinuous because turbid water obscured the bed on several occasions. Vertical bars show the uncertainly. Upward arrows indicate minimum values. Uncertainty stems primarily from accumulation of a plowed wedge of sediment on the up-glacier side of the hole. Note that, contrarу to expectation, ub appears to lead both us and Pe, and Pe leads us
Actually, u s − u b may decrease when u s increases. This conclusion is based on earlier studies (Reference Hooke,, Calla, Holmlund,, Nilsson and StroevenHooke and others, 1989), using a force-balance approach, that suggested that increases in surface speed lasting a few days are associated with reductions in τ b.
Discussion
Features of Figures 3 and 4 that merit discussion are: (1) the lack of significant variation in the dragger record, despite the large variation in P e and u s, (2) the lack of correlation between force on the ploughmeter and u s, and (3) the fact that P e and tilt rate are in phase. First, however, a comment on the negative tilt rates is in order.
Negative Tilt Rates
Negative tilt rates at low P e are a common feature of our data (Figs 1, 2 and 3) and were also observed by (Reference Blake,Blake 1992; see Reference Blake,, Clarke and Gérin.Blake and others, 1992). At first, we attributed this to bed-parallel compression of the till as hydraulic lifting of the ice permitted thickening of the till layer. However, in ring-shear experiments, Reference Iverson, and BakerIverson and Baker (in press) have found that elastic strains are accumulated during initial phases of deformation and that reverse creep then occurs when the load is removed, even after large strains. Thus, consistent with Reference Fischer,Fischer (1995, p. 85) and Reference Fischer, and Clarke.Fischer and Clarke (in press), we infer that the negative tilt rates observed in subglacial experiments actually reflect elastic upslope movement of the upper part of the till layer as the ice is gradually decoupled from the bed.
The Dragger Record
The relation between the force on the dragger, F (N), on the one hand, and τr, and P e (Pa) on the other, can be estimated using the relations:
(Reference Iverson,, Jansson and HookeIverson and others, 1994, equations (7)). The constant factors arc calculated using с ≈ 0 and ϕ r = 25.5 ° where ϕ r is the friction angle applicable to highly deformed till in the residual state. These values are based on laboratory measurements on samples of Storglaciären till sheared in our ring-shear apparatus (Iverson, unpublished data). Earlier measurements in direct-shear tests (Reference Iverson,, Baker and HooyerIverson and others, 1994) or based on less complete ring-shear data (Reference Iverson,, Hanson, Hooke and JanssenIverson and others, 1995) yielded higher values of ϕ r. However, in the case of the direct-shear tests, the boundary constraints and limited shear strains are less appropriate for determining values applicable to residual strength.) The mean F is ∼408 N, so τ r ≈ 52 k Pa and P e ≈ 0.11 M Pa. The latter is virtually identical to the measured mean value (Fig. 3).
The 1.2 N range in drag (Fig. 3) corresponds to a range in P d of 0.3 k Pa, whereas the measured range is 85 k Pa. In this part of the glacier, as mentioned earlier, the water pressure in boreholes is inferred to reflect a global pressure transmitted through numerous englacial conduits (Reference Hooke,, Pohjola, Jansson and KohlerHooke and Pohjola, 1992) rather than the (mean) pressure in the water layer at the ice – till interface. Thus, we infer that the pressure fluctuations in the vicinity of the fish were damped, relative to those in the borehole, by passage through till. The record in Figure 2 starts 24 d after insertion of the dragger (whereas that in Figure 1 begins only 4 d after insertion), so it is reasonable to suppose that the fish had been drawn into a region of relatively pristine till, uninfluenced by the drilling and far enough from the original hole to damp pressure fluctuations.
Such a large amount of damping implies a substantial lag between the diurnal water-input forcing and the till P e response. The time-scale for pore-pressure equilibration can be approximated by d 2/к where d is the length-scale over which pore-pressure diffusion occurs and к is the hydraulic diffusivity. A reasonable value for к, based on measurements with the ring-shear device, is 2.5 ± 1 × 10−6 m2 s−1 (Reference Iverson,, Baker and HooyerIverson and others, in press). If peaks in the dragger record actually lag those in P e by ∼1 d, the implied value of d is 0.45 ± 0.1 m. A lower limit for d is 0.10 m, the length of the wire from the fish to the bottom of the tube leading to the load cell, However, tubes recovered from previous experiments have been bent, presumably at the ice – till interface. Furthermore, till may have been forced upward into the bottom of the bore-hole. Such a sediment column would increase d above its minimum value; 0.45 m is on the high side but not unreasonable.
The amount of damping of the P e signal, from 85 to ∼0.3 k Pa, is also consistent with this hypothesis. In a semi-infinite medium subject to a sinusoidal pressure variation of amplitude ∆P 0 at the surface, the amplitude of the variation at depth. z, ∆P z, is;

where ω is the period of the variation, in this case 2π d−1 (Reference Carslaw, and JaegerCarslaw and Jaeger, 1959, p. 65; Reference Hooke,Hooke, 1976, Equation (2)). In the present case, damping is greater because the pressure signal is spreading out along a more-or-less spherical front. A reasonable supposition is that the damping will be increased by (d 0/d)2 where d 0 is a reference distance from the center of the borehole at which distance the amplitude is equal to that in the borehole. If the diameter of the bore-hole at the bed is ∼0.15 m, a reasonable value for d 0 is half that. Thus, using d = z = 0.45 m, the amplitude of the variation at the fish should be ∼0.4 ± 0.3 k Pa, in reasonable agreement with observation.
The dragger record does not appear to reflect variations in u
b. Indeed, the inferred surface-speed record is about ![]() d out of phase with the dragger record. Thus, for example, the force on the fish was decreasing while u
s was peaking. The variations in u
s are likely to have been >30 mm d−1, as variations in u
s measured a week prior to the beginning of the record in Figure 2 were of this magnitude at a time when the mean Pe was higher, and the variations smaller. Because the strain rate induced in the till by movement of the fish must be proportional to the rate at which the fish is dragged through the till, the strain rate was presumably varying appreciably without resulting in significant variations in force on the fish. This supports a flow law of the form of Equation (4). (It is, of course, possible that the till surrounding the fish was always moving at the same speed relative to the ice. This, however, is inconsistent with our explanation of the negative tilt rates at low Pe.)
d out of phase with the dragger record. Thus, for example, the force on the fish was decreasing while u
s was peaking. The variations in u
s are likely to have been >30 mm d−1, as variations in u
s measured a week prior to the beginning of the record in Figure 2 were of this magnitude at a time when the mean Pe was higher, and the variations smaller. Because the strain rate induced in the till by movement of the fish must be proportional to the rate at which the fish is dragged through the till, the strain rate was presumably varying appreciably without resulting in significant variations in force on the fish. This supports a flow law of the form of Equation (4). (It is, of course, possible that the till surrounding the fish was always moving at the same speed relative to the ice. This, however, is inconsistent with our explanation of the negative tilt rates at low Pe.)
The Ploughmeter Record
The force on the ploughmeter could be influenced by the strength of the till, by the speed with which the ploughmeter is dragged through the till, or on a finer scale by impacts with clasts in the till (Reference Fischer, and Clarke.Fischer and Clarke, 1994). The record (Fig. 4) suggests that the first of these effects dominates; there is a clear relation between the effective pressure and the force on the ploughmeter. This is consistent with the earlier conclusion that high water pressures (low Pe) weaken the till (Equation (2)).
Lagged correlations suggest that variations in P e lead those in force on the ploughmeter by ∼0.3 d. This lag implies a length scale, d, of ∼0.25 ± 0.05 m. The ploughmeter is rigid, so its tip should remain directly beneath the bore-hole. In contrast, the fish on the dragger should be decimeters up-glacier from the bottom of the borehole after a few days. Thus, a lower value of d for the ploughmeter is reasonable. On the other hand, the wavelength of the fluctuations in P e in Figure 4 is several days. This, combined with the lower d, would serve to decrease damping of the P e signal as experienced by the ploughmeter compared with damping experienced by the fish.
In contrast, there is no significant correlation between the force on the ploughmeter and surface speed. Assuming, as before, that changes in u s reflect changes in u b, this again implies that the force on the ploughmeter is only weakly influenced by the speed with which it is drawn through the till. Thus, a rheology of the form of Equation (4) is again implied.
Till-Water Pressure
The pressure transducer embedded in till yielded an interesting record. For the first 50 d, during which the borehole presumably moved ∼2 m from the position of the transducer, the water pressure in the till tracked that in the same and nearby boreholes closely. Then, it began to rise slightly above the others (Fig. 5) but, through mid-September, it tracked their variations without lag. Thereafter, the pressure in the till increased further, reaching a maximum of ∼200 k Pa above that in the boreholes in early October. By late December, it was recording a pressure ∼80 k Pa above the overburden pressure.
The lack of lag in late August suggests that, even after the transducer was far enough from the borehole that it could show a different (higher) water pressure than that in the borehole, there was still a direct hydraulic connection between the transducer and the borehole. According to the manufacturer, the transducers are constructed in such a way that, even if water leaks into the cable, it cannot influence the pressure at the sensor, so we rule out a connection through the cable. As the transducer was inserted only ∼0.1 m into the till, we suspect that it may have migrated to the ice – till interface and was sensing pressure in a water layer at this interface. If this is the case, the thickness of the water layer, h, may be estimated from:

(derived from Equation (7) of Reference Weertman,Weertman (1972)). Here, R is the radius, taken to be ∼10 m, from which the borehole receives water generated by a basal melt rate, ṁ (∼10 mm year−1; Reference Östling, and Hooke.Östling and Hooke, 1986), μ is the viscosity of water at 0 ° C (∼0.0018 kg m−1 s−1), u b is the sliding speed (40 mm d−1), dP/dt is the increase in pressure in the till with time as the borehole moves away from the transducer (∼0.016 Pa s−1; Fig. 5), and r is the distance from the center of the borehole to the transducer. Using the above values, h ≈ 0.2 mm 2 m from the borehole and decreases to ∼0.1 mm 6 m from the borehole. These appear to be reasonable values and thus the lack of any lag in this case is not inconsistent with the dragger and ploughmeter data.
Tilt and P e
The association of high tilt rates with high effective pressures suggests that the coupling between the ice and the bed improves as P
e increases and conversely (Figs 1 and 3). Suppose that the shear stress applied to the till were to be given by τ = μΡ
e where μ is a coefficient of friction. Then, if μ were constant, P
e would serve as a proxy measure of τ. Since we know ![]() from the tiltmeter data, various constitutive relations between
from the tiltmeter data, various constitutive relations between ![]() and τ could then be tested by plotting
and τ could then be tested by plotting ![]() against P
e. Such a plot, using the stacked data, yields a linear relation. (This would correspond to n = 1 in Equation (1).)
against P
e. Such a plot, using the stacked data, yields a linear relation. (This would correspond to n = 1 in Equation (1).)
Such an interpretation conflicts with our explanation, above, of the dragger and ploughmeter data. We thus conclude that μ is not constant. Rather, it is probable that, as the water pressure decreases, the thickness of a water layer at the ice – bed interface decreases. This is consistent with the measured increase in pore-water pressure in the till during the fall, mentioned above. As h decreases, the ice would contact an increasing number of particles in the bed, resulting in an increase in μ as P e increases.
Conclusions
Consistent with Equation (2). We find a strong correlation between effective pressure and till strength (Figs 3 and 4). Thus, it appears that Storglaciären till, like many other granular materials, is a Mohr – Coulomb or frictional material. The excellent agreement between the measured P e and that calculated from the second of Equations (6), using the value ø determined in the laboratory (23.5 °), suggests that laboratory, measurements can be used to characterize till properties.
The lack of correlation between till strength and surface speed suggests that the residual strength does not vary significantly with strain rate. This is consistent with geotechnical experiments which suggest a constitutive relation of the form:
where τ0 is a function of P e (Equation (4a)).
As P e increases, the coupling between the glacier and the bed increases, as expected. However, the increase is non-linear and thus cannot be described in terms of, say, a constant coefficient of friction.
Acknowledgements
We appreciate the energetic assistance of D. Cohen. T Dahlgren, N. Grace, J. Johansson, H. Laudon. F. Neidhart, В. Norell and J. Petersson in the field, and the constructive comments of G. K. C. Clarke and J. W. Jenson on the manuscript.
This research was supported by the U.S. National Science Foundation grants DPP-88-22156, OPP-92-24209), OPP-92-24175 and INT-92-13833. and by the Swedish Natural Sciences Research Council.