Introduction
The Pleistocene glaciers left many signs of their passage; some of the most remarkable are the low, smooth hills known as drumlins. Drumlins have been observed and investigated for a considerable time but to date no completely satisfactory theory has been evolved to explain their formation. Several factors appear to be involved and the problem of choosing the significant and avoiding the irrelevant is very difficult. This paper represents the development of the theory, already published in outline (Reference SmalleySmalley, 1966[b]), that the formation of glacial-till drumlins is a consequence of the dilatancy of the material of which they are composed. Most drumlins are formed from till, a material with very complex rheological properties and this paper is mainly concerned with these, but any other formation which may be called a drumlin (e.g. a rock drumlin) is also considered.
The drumlins we see now were formed in the Pleistocene and like most aspects of Pleistocene geology there is a vast literature relating to them. Literature up to the mid-1950s has been surveyed by Reference CharlesworthCharlesworth (1957) in his great compendium. He does, however, tend to concentrate on an assessment of theory and opinion rather than on the collection of available drumlin facts. The best collection of drumlin-shape and size data is probably still that by Reference EbersEbers (1926). There have been several notable papers since the Charlesworth survey and these are discussed in later sections of this paper.
Two questions need to be answered to provide an explanation of the observed nature of drumlins. These concern (1) the nature of the geomorphic force which shaped the drumlins, and (2) the way in which the force accomplished the shaping. The necessary geomorphic force is generally ascribed to the action of glaciers, so only one problem remains, that of the mode of interaction of the glacier and the terrain which leads to the formation of drumlins. The consequences of this interaction are low streamlined hills which tend to occur in groups or fields and within these fields they have a certain distribution of orientations and certain positional relationships.
In this paper the formation of the drumlins is explained by invoking the dilatancy mechanism, the shape by the requirements for streamline flow, and the orientation is simulated by a random model. The distribution of drumlins in a drumlin field has been investigated in two ways. Random models have been produced and the spacings of drumlins in these compared with the measured spacings of real drumlins, and drumlin-spacing data derived from maps have been analysed for indications of random spacing. Both approaches indicate that drumlins do occur at random within drumlin fields.
Formation
The relative scarcity of drumlin forms suggests that the conditions necessary for their formation were rigorous, and infrequently achieved. It is proposed that the basic conditions for the formation of glacial-till drumlins were:
-
i. The glacier–terrain relationship was such that at the base of the glacier the terrain material was being continuously deformed. Some of this terrain material was carried along by the glacier so that shear deformation occurred within the terrain material.
-
ii. The deformed layer was composed of a concentrated dispersion of boulders and large rock particles in a dense clay–water system, the material usually called boulder clay or glacial till. For drumlins to form, the large particles in this till layer had to form a dilatant system.
Dilatancy is a property of granular masses. When a granular mass, for example some dry sand, is at rest, it forms a stable heap and the particles in the heap are relatively closely packed together. When the granular material is deformed, it expands; this is the phenomenon of dilatancy, first observed by Reference ReynoldsReynolds (1885), related to geology by Reference MeadMead (1925), and fully investigated by Reference Andrade and FoxAndrade and Fox (1949). There is no completely satisfactory definition of dilatancy. Reference BoswellBoswell ([1961], p. 73) stated that dilatant systems are those in which the anomalous viscosity increases with increase of shear. This is just an elaborate way of saying that dilatant materials are more resistant to shear stresses than might be expected. It is the high resistance to initial deformation of till which leads to the formation of drumlins.
The dilatancy of granular masses under compressive and shear stresses has been demonstrated using the simple apparatus illustrated in Figure 1a. A cylindrical ram of diameter 7·5 cm is forced down at a constant rate by a hydraulic press into a cylindrical container of diameter 15 cm which contains dry sand of particle size about 0·5 mm. A graph showing load vs deformation (i.e. ram travel) is produced automatically by the machine recorder as shown in Figure 1b. When the load is first applied, the sand aggregate starts to expand because its natural close packing is being disturbed and a more open packing is developing. The material continues to expand and to resist deformation until it reaches the state of maximum expansion, at point Ain Figure 1b. Further deformation causes a collapse and the required deforming load drops; point b on the graph is reached and further deformation only requires loads of about this magnitude.

Fig. 1. The dilatancy of granular materials. a. Simple device for demonstrating dilatancy; b. Load-deformation curve for dry sand; c. Load-deformation curve for a glacial till.
The curve shown in Figure 1b is an ideal example produced with dry sand as the granular medium. A curve of similar form is produced when dilatant glacial till is deformed from rest. The constraints produced by the container are more noticeable when the till is deformed and because of these constraints quantitative measurements were not attempted; unfortunately an uncomfortably large container would be required to eliminate the constraints. The very large particles in the till cause irregular deformation but the general shape of the load-deformation curve (Fig. 1c) is similar to the ideal model case shown in Figure 1b.
In the suggested drumlin-forming mechanism the glacial till is being continuously deformed by the movement of the glacier and a stress level in the general range indicated by c in Figure 1b and c is involved. Within the thin deformed layer of till there is a certain variation in stress level. If the stresses drop below level b then the expanded material collapses into the static stable form and there are no stresses of magnitude a available to cause sufficient dilation to get the compacted material moving again so the flowing till flows around it, shaping it so that it causes the minimum of disturbance in the flowing stream of till.
If the glacier–terrain relationship is such that the general stress level is greater than a, then no drumlins can form; the glacier sweeps all before it. If the general stress level is below b, no drumlins can form because continuous deformation of the till is impossible. In most large continental glacier systems one would expect the mean stress level to be greater than a so that most tracts of glaciated land have no drumlins. Towards the periphery of the ice sheets the stress levels drop and there is a region in which the stress levels are such that drumlins form and farther towards the periphery the stress levels drop too low to allow drumlin formation and end-moraine structures form. The drumlins form when the general stress level beneath the ice sheet is in the region represented by range c in Figure 1b and c, i.e. below a but above b; this is illustrated diagrammatically in the ice-sheet section shown in Figure 2. Fairly rapid thinning might be expected to occur at the edges of large ice sheets, giving rise to a relatively narrow drumlin belt. Small local glaciers, such as covered the northern half of Ireland during the late Weichsel glaciation, mostly produced stress levels in the c range and thus very large and extensive drumlin fields exist in Ireland.
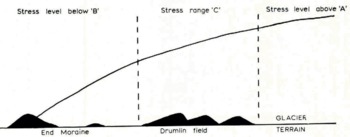
Figure 2 Cross-section al the edge of the ice sheet with critical stress regions indicated.
It is the large rock fragments in glacial till which make it dilatant; it may be that the clay part of the material is thixotropic and thus aids the shaping process. When part of the till layer packs into an obstruction, a local high-pressure zone is formed as the rest of the till layer flows past the obstruction. Under the influence of this local high pressure the clay part of the till becomes more fluid. The more fluid clay flows more easily around the obstruction carrying the large particles with it and giving the obstruction a smooth streamlined shape. The phenomenon of thixotropy is even more difficult to define satisfactorily than that of dilatancy. The two phenomena are effectively opposites in that thixotropic materials are less resistant to shear stresses than might be expected. A well-known example of a thixotropic material is non-drip paint; in the can this appears almost solid but under the pressure of the brush it flows quite smoothly and easily. In the same way the till clay flows more easily at the drumlin–till flow interface and thus facilitates the formation of a smooth streamlined shape.
Thus the model for the drumlin-forming mechanism depends on two postulates: that the glacier is separated from the terrain by a continuously deformed layer of till, and that within this till layer there is a range of stress levels. The drumlins formed are basically accretional forms, although the material is gathered by local erosion; this falls in fairly neatly with the views of Reference ThornburyThornbury ([1954], p. 391). He described drumlins as characteristically lying several miles to the back of end moraines and suggested that their streamlined forms indicated lodgement of till, with subsequent over-riding and reshaping by the ice. He also suggested that drumlin development just behind end moraines may possibly be related to rapid thinning of the ice in this zone; this is the state of affairs illustrated in Figure 2.
If the continuously deformed till-layer postulate is discarded (the action being justified by reference to Occam’s razor), a related erosional mechanism suggests itself. It can be imagined operating in Ireland where the late Weichselian glaciers advanced over morainic material resulting from an earlier glacial phase. Within this earlier till there was a certain distribution of relatively large rock fragments, in some places more tightly packed together than in others. The glacier advanced with stress level c in operation at the working interface and, while the till with the loose packing of boulders was smeared easily across the landscape, the till patches with the high boulder content were obstinately dilatant. For the closely packed parts to be eroded they had first to expand but the weight of the glacier pressing down prevented them from doing so. The glacier provides the eroding force but, paradoxically, this very force prevents erosion. The obstruction, very closely packed by the passage of some of the ice, was sculptured into the most convenient shape as the glacier forged on. The most convenient shape was the one which caused the least interference with the flow pattern; this was a streamlined shape (Reference ChorleyChorley, 1959) and thus drumlins achieved their characteristic form.
Drumlins formed from older, stratified drift material are presumably formed by this simple mechanism and drumlins formed from the latest drift are formed by the more complex method. Actually, both can operate at the same time, and must in fact necessarily do so. There is, as Reference GravenorGravenor (1953) noted, both an erosional and a depositional aspect to the formation of drumlins. Reference AronowAronow (1959) suggested that to explain the phenomenon of drumlin formation recourse must be had to “something” in the now vanished ice. He was only very slightly off target, and it is suggested that this “something” was the dilatancy of the till.
Reference FlintFlint ([1957], p. 68) stated that “ … there is a complete gradation, independent of outward form and within a single field, from rock to drift. This suggests that any one group was molded contemporaneously under a single set of conditions”. Within the various forms there will be basic material requirements; solid obstructions will require stresses far above the a level in order to be eroded away completely, these gain an accretionary smoothing of clay to give streamline flow contours. The drumlins with high boulder contents also represent zones of resistance because the material was dilatant and required stresses consistently at the a level for complete erosion. As the rock content decreases a minimum point is reached where the mean e level stresses at the glacier–terrain interface cause erosion so effectively that no drumlins can form. Thus drumlins can have assorted contents, provided the minimum rock or boulder content is reached.
It will be seen from Figure 2 that due to the rapid thinning at the periphery of the ice sheet the critical stress range at the a level is passed through much more slowly than the critical stress at the b level. In other words, the area where the drumlin-forming mean stress level c is operating is bounded at the up-stream side by a fairly diffuse boundary and on the downstream side by a more precise boundary. If a drumlin field could be examined in its entirety, it should exhibit a concentration of drumlins near the fringe of the ice sheet, behind the end moraine, and the frequency of drumlins should decrease in the parts of the field which were farther under the ice. When the general stress level drops below the a range, drumlins may begin to form but the general stress level is too high for large-scale formation; an occasional drumlin forms, possibly with an elongated shape due to the relatively high ice pressure. The stress level drops as the ice thins and more drumlins form. As the edge of the ice sheet is approached the ice thins rapidly and the stress level drops rapidly below the critical b range. At this level the glacier is still an efficient debris transporter arid the carried till load is eventually dumped as end moraine.
Shape
Two methods have been advocated to describe the shape of drumlins. Reference ChorleyChorley (1959) has proposed that the plan form of the drumlin can be described by a polar equation of the form ρ = l cos kθ. In this equation l is the length of the drumlin, k is a dimensionless number which effectively indicates the width of the drumlin, ρ and θ are the two variables. Reference ReedReed and others (1962) preferred to use an equation of the form
This produces an ellipsoid with its centre at the origin; a, b and c are the semi-axes, and x, y and z are the rectangular coordinate directions.
Each method has advantages and disadvantages, but the Chorley method appears to be the more useful. The disadvantages of the Chorley method are that it only operates in two dimensions and the equation is in polar coordinate form which is perhaps more difficult to manipulate than the more common rectangular coordinate system which is used by Reed and others. The great advantage of the Chorley method is that the value k serves to classify the shapes of drumlins; if the value of k is known then the shape of the drumlin is known. The other desirable thing about the Chorley equation is that it is obviously related to the mode of formation of the body it describes. It is accepted that drumlins are a consequence of glacier flow and flowing systems flow most easily around a streamlined object. Chorley’s equation is that for a streamlined form; actually it is a slight simplification but in terms of goodness of fit and simplicity it is the best available.
Reed and others claimed no particular advantage for their representational method but it appears to have two: it gives a three-dimensional model and it works in rectangular coordinates. Actually, these advantages are relatively trivial and are completely overshadowed by the method’s overwhelming disadvantage—that it lacks the physical meaning which Chorley’s model has. Reed and others decided that drumlins have ellipsoidal shapes and stated the equation for an ellipsoid without really considering the consequences or implications of either the observation or the equation.
The value k has been calculated by Reference ChorleyChorley (1959) for some drumlins described by Reference AldenAlden (1905). He gave values for 23 drumlins; the mean value was just under 6 and the mode value was between 3 and 4. If comparisons are to be made with these pioneering values of Chorley, then it is necessary to facilitate the production of k values for observed drumlins. Figure 3 is a nomogram devised to convert the width–length ratio (w/l) into the k value. The curve of ρ = l cos kθ was drawn for different values of k and the widths were measured, the length l remained constant. The w/l ratio was then plotted against k to produce the graph shown in Figure 3. The w/l ratio is preferred to the l/w ratio because the limits are 0–1 (real) rather than 1−∞ (unreal).

Figure 3. Variation of Chorley value k with width/length ratio for lemniscate-type curve.
Reference CharlesworthCharlesworth (1957, p. 389) has given some data for average dimensions of drumlins, indicating that the mean w/l ratio is of the order of 0.40; this gives a k value of just under 3. Some more recent observations by Reference HeidenreichHeidenreich (1964) include values of l and w for Canadian drumlins. He found that in the four drumlin fields investigated w/l ratios decreased fairly uniformly until a critical width was reached, after which the drumlins could increase in length while width remained constant. Drumlins appeared to be divisible into two distinct populations, those of k value around 3–4 and those of high k values which usually had reasonably constant width within the same field. Heidenreich stated that until constant width was reached, width and length increased fairly constantly at a ratio of 0.37 which gives a k value of 3. It appears that a k value of about 3 is the most usual.
Distribution
If either the accretionary or the erosional or, as seems most likely, both, mechanisms are working to produce drumlins their distribution might be expected to be completely random, or in other words there is no reason to expect a non-random distribution. Within the boundary conditions for drumlin formation the most important variable is probably the variation of properties in the available glacial till and these can be expected to vary randomly. The distribution of drumlins has been investigated in two ways. A random model has been devised and the distribution of drumlins in the model field has been compared with the observations of Reference ReedReed and others (1962) and Reference VernonVernon (1966), and drumlins in real fields have been subjected to nearest-neighbour analysis.
Random-placement model
The random process used to produce the model was devised initially to give one-dimensional random packings (Reference SmalleySmalley, 1962) for subsequent comparison with three dimensional packings of sedimentary particles (Reference SmalleySmalley, 1964). To produce a model of a drumlin field, the method must function adequately in two dimensions; it has been applied successfully in two dimensions in producing models of crack systems in lava flows (Reference SmalleySmalley, 1966[a]).
The terrain is represented by a square 100 × 100 frame (the numbers have arbitrary units). The glacier flows over this chosen piece of terrain and drumlins are formed within the square demarcation. The drumlins are placed at random, the points at which they occur being indicated by coordinates taken from a set of random-number tables. A very suitable set of tables is that by Reference Kendall and SmithKendall and Smith (1951); this gives lists of two-digit random numbers between 00 and 99 which arc ideal when taken in pairs to represent positions within the square field. Two adjacent sides of the square frame are considered as axes, the first two-digit number of a pair represents the x coordinate, the second number the y coordinate. The plotted point marks the stoss end of the drumlin. The number of points plotted depends on the density of drumlins in the field; the mode density according to Reference CharlesworthCharlesworth (1957, p. 389) is 3 per square mile. Thus if the side of the square frame represents 2 miles, 12 random points are needed.
In this model some overlaps will probably occur, giving rise to some rather odd shapes and this also appears to occur in nature. It is possible, for comparison, to produce a model in which overlaps do not occur. Each drumlin is drawn in as soon as its position is known and any subsequent drumlins which would overlap are rejected.
To produce a model field containing 12 drumlins the following procedure would be adopted: 12 random points are plotted in the square field and a drumlin is drawn, using a template, for each point. Some of these drumlin shapes will overlap giving several larger, more complex drumlins. Each of these larger drumlins counts as one so more coordinates are plotted until 12 distinguishably separate drumlins are formed; this is the model distribution and spacing measurements can be made and compared with real fields. Reference ReedReed and others (1962) made perpendicular and parallel measurements which are difficult to define and make. The Reference VernonVernon (1966) direct measurements are capable of a more rigorous definition; every drumlin has two measurements associated with it. These are the distances of the two nearest drumlins in an up-stream direction, one on each side of the long axis of the reference drumlin.
In order to produce a comprehensive set of measurements of the drumlin in the random-model field special boundary conditions have to be introduced for the field otherwise the drumlins near the edge have no adjacent drumlin. The edge effect is eliminated by introducing edge drumlins into special adjacent fields. If a drumlin is placed at 05 51 by the random number coordinate then one is also placed at 105 51; similarly, one at 62 02 has a corresponding placement at 62 102. This has the effect of producing a closed field so that every drumlin has the required neighbours. Overlaps at the top are introduced at the bottom and so on. A sample field is shown in Figure 4; the measurements taken are indicated. Four closed fields were produced, each containing 24 drumlins. Each field yielded 48 measurements and these were amalgamated to produce the histogram shown in Figure 5; this should be compared with the histogram produced by Reference VernonVernon (1966) from similar measurements on the Ards Peninsula drumlins, a distinct similarity is apparent.

Figure 4. Drumlin-field model produced by random placement of drumlins in a square field; edge of field represents a length of 4 572 m. each drumlin is 457.2 m long.

Fig. 5. Histograms of direct spacings of drumlins. a. Data from four random-placement models; b. Data from Reference VernonVernon (1966). observations of Irish drumlins.
Nearest-neighbour analysis
It is possible to test the fit between a natural field and a random model without recourse to direct simulation since the “nearest-neighbour” statistic tests the manner and degree to which the distribution of individuals in a population in a given area departs from that of a random distribution. The statistic, which was devised initially for use in the biological sciences by Reference Clark and EvansClark and Evans (1954) and has since been used in settlement geography (Reference HaggetHagget, [1965]), is defined as:
where D obs is the linear distance between any one point in a specified area A and the nearest neighbouring point, and N is the number of points within the area. The statistic is such that values of R range from zero for maximum aggregation to 2.1491 for maximum (hexagonal) spacing. Random distributions give values of unity. However, it is important to note, as Clark and Evans pointed out, that a random distribution in this sense is defined as one in which any point has the same chance of occurring on any sub-area as any other point, and that any sub-area of specified size has the same chance of receiving a point as any other sub-area of that size. So defined, randomness is a spatial concept, depending upon the boundaries chosen. Thus a distribution may be random with respect to one area but non-random with respect to a larger area which includes it.
The method can be easily applied to a drumlin field. Natural patterns are taken off either aerial photographs or maps of any scale consistent with identification of the features and the nearest-neighbour distances are found for a specified number of individuals within a sub-area. This is to eliminate side effects; a drumlin’s nearest neighbour may fall outside the area A chosen. The distances are summed and a mean value D obs calculated. Knowing the area, values of R can be calculated directly.
Table I presents the results of such an analysis performed using 1: 25 000 topographic maps for small areas in Ireland, and one in England. Recognition of drumlins on the maps was done on the basis of contour pattern, drumlins being recognized where ellipsoidal patterns occur. This may result in the recognition of some forms which are not drumlins, but it is thought that the bias introduced is not great. Figure 6 shows the field which was used in England.
Table I. Nearest-neighbour Analyses for Four Natural Drumlin Patterns


Fig. 6. Drumlin distribution in the Vale of Eden.
As the table shows, the R values derived for natural patterns range from 1. 1295 to 1.3842, indicating that the distribution lies somewhere between “uniformly spaced” and “random”, as the figures are usually interpreted. It should be noted, however, that the random-placement models gave R values of 1.1500, 1.0441, 1.2766 and 1.1367, indicating that the real distributions are actually truly random.
In general, both methods used indicate that the drumlin fields examined contain a random distribution of drumlins.
Orientation
If a closely packed drumlin field is produced by the random-placement method, there will be considerable overlapping. Figure 7A shows a close packing of drumlins in which the outlines have been slightly modified to produce coalescence and a smooth outline for the complex drumlins. This produces some drumlins of a more complicated shape and having orientations which do not lie exactly along the line of glacier travel. The direction of glacier travel is chosen at random after a suitable number of location points have been plotted. In Figure 7A the apparent drumlin axes are marked; the orientations have been measured and the results are shown as a histogram in Figure 7B. A normal symmetrical distribution of orientations is produced; this agrees exactly with the orientation measurements on real drumlins reported by Reference ReedReed and others (1962).

Fig. 7. Orientation of drumlins. A. Random-placement orientation model; B. Histogram showing normal distribution of orientations about chosen glacier flow direction.
Discussion
Initially, the rigorous nature of the postulated boundary conditions suggests that drumlins should only rarely be observed in nature. Most authors who have written on the subject have agreed that this is the case. Fairchild (see Reference AldenAlden, 1911, p. 734) spoke of “The combination of several factors which do not commonly occur in nature”, whilst Reference AronowAronow (1959) considered drumlins to be related to “unknown conditions” which are not simply related to either the terrain or to the nature of the available materials. The dilatancy mechanism suggested requires both that the material be dilatant and that the stresses within the glacier system are within a certain critical range, and it is suggested that these are the “unknown conditions”.
Available evidence indicates that drumlin fields are to be found in bands paralleling, and some distance to the rear of, end moraines. Reference VernonVernon (1966) has noted that the drumlin fields of eastern Ireland are bounded to the south by the Carlingford Re-advance moraine, whilst Reference AldenAlden (1911) showed that in eastern Wisconsin the drumlin fields are confined to a zone within 30 to 50 miles (48 to 80 km) of the limits of an ice lobe where the ice was radiating towards its margin. He suggested that the height of ice cover over the drumlin field varied from 1 450 ft (442 m) over the initial part to 450–830 ft (137–253 m) where drumlins cease to be found, some 5 miles (8 km) from the limit of the advance. Reference TaylorTaylor (1931) noted that drumlins occur in wide basins or lowland areas such as some of the Great Lakes basins and the lowlands of Ireland, Scotland and Scandinavia, suggesting that either dying or slowly moving ice is an essential pre-requisite to their formation. Similarly, Reference AronowAronow (1959) has noted that there is a continuous gradation from perfect drumlin forms through drift patches to true end moraine; this is a critical observation since this is exactly what would be expected if the dilatancy mechanism were responsible for drumlin formation. As the stress level falls below the lower critical level B, drumlins cease to form and end-moraine material may begin to be deposited.
The observed distribution of drumlins relative to each other is as would be expected from the dilatancy mechanism. As Reference FlintFlint ([1957]) pointed out, single isolated drumlins are rare, possibly indicating that certain boundary conditions are involved and that a definable stress range is required for drumlin formation. This tends to occur over a relatively wide area when it does occur, although within a large ice sheet covering a large area of suitable terrain the occasional anomaly may occur to produce an isolated drumlin.
It has been the usual practice to divide theories of drumlin formation somewhat arbitrarily into erosional and accretional ones. Reference AronowAronow (1959) placed in the erosional group suggestions by Reference GravenorGravenor (1953) and Reference FlintFlint ([1957]), and in the accretional group theories by Reference ThwaitesThwaites (1957), Reference ThornburyThornbury ([1954]) and Reference CharlesworthCharlesworth (1957). Reference ReedReed and others (1962) observed the traditional dichotomy but also suggested that both erosion and deposition must be involved.
Few, if any, of the so-called theories are actually theories, if a theory is required to account for the formation of the streamlined hill of till or rock. Most “theories” are really suggestions for boundary conditions within which some unspecified process operates, and the stipulated conditions may be remarkably imprecise. They are perhaps none the worse for that and it is dangerous to be too precise with very little data to base judgements on and, although much has been written about drumlins, very little hard fact has emerged. Only recently, in accordance with the general trend in geomorphology, has the quantitative investigation of drumlins and drumlin fields been undertaken. Reference ChorleyChorley (1959) has given a meaningful interpretation of the shape of drumlins; Reference ReedReed and others (1962) have measured distributions and orientations, and Reference VernonVernon (1966) has measured spacings and distribution; these three papers represent the basis of the new approach to the problem of drumlin formation.
Reference VernonVernon (1966) has suggested that drumlins form when ice flow induces a pressure differential between the front and back of an obstacle. Pressure melting at the front of the obstacle creates a zone of greater mobility in the ice which moves to the zone of low pressure behind the obstacle, leaving the debris behind as till; presumably in front of the obstacle. The idea of pressure melting is attractive and obviously feasible but there are objections to incorporating it into the drumlin-forming mechanism. If the glacier is moving enough till to subsequently form a drumlin or an end-moraine deposit, the bedrock obstacle, unless it is drumlin-sized itself, will tend to be insulated from the actual ice by the till load. Also, the fact that pressure melting may be involved does not throw any light on the problem of drumlin distribution.
Reference GravenorGravenor (1953) has listed ten conditions which must be satisfied by a theory of drumlin formation and these can be summarized as follows:
-
Drumlins may consist of a variety of materials.
-
They may have layers of stratified materials which may be faulted or folded.
-
Rock and till drumlins have the same shapes and occur in the same fields.
-
Many glaciated areas do not have drumlins.
-
They occur in fields which are wider than most moraines and they rarely occur singly.
-
They have a streamlined shape with the blunt end pointing up-stream.
-
Lamination may be present.
-
Some drumlins may have cores but most do not.
-
Drumlins are found behind end moraines.
-
They are aligned parallel to the ice-flow direction.
It is suggested that the dilatancy theory provides a mechanism which satisfies these conditions, and especially those relating to distribution (numbers 4, 5 and 9). Perhaps one further condition could be added to Gravenor’s ten:
11. They are formed beneath temperate glaciers.
The suggestion by Reference NyeNye (1965) that temperate glaciers slip on their bed is to some extent supported by the observation of Reference MacNeillMacNeill (1965) that there appeared to be free water present when some of the drumlins in south-western Nova Scotia were formed. A glacier whose bottom ice is below the melting point probably does not slip on its bed and thus cannot form drumlins.
Conclusions
A comprehensive theory of drumlin formation can be derived from two basic precepts: (a) glacial-till drumlins are formed from dilatant material, and (b) they were formed when the stresses in the till-glacier interface zone were within certain critical limits. There must be deformation of the actual till, which is the dilatant material. The bulk of transported till may be carried within the ice sheet; for drumlins to form there must be shear deformation in till at the glacier-terrain interface. It may be that this requires the ice to be advancing over already deposited till.










