1. Introduction
Ice cores from drilling sites of the European Alps have been widely used as environmental archives to reconstruct the deposition history of aerosol-related species over the 20th century (Reference Wagenbach, Münnich, Schotterer and OeschgerWagenbach and others, 1988; Reference Preunkert, Wagenbach, Legrand and VincentPreunkert and others, 2000, Reference Preunkert, Legrand and Wagenbach2001; Reference Schwikowski, Cecil, Green and ThompsonSchwikowski, 2004). Less effort has been made, however, to investigate climate-related long-term records from these archives (Reference Wagenbach, Preunkert, Schaefer, Jung, Tomadin, Guerzoni and ChesterWagenbach and others, 1996), since the glaciological settings are much more complex at Alpine than at polar drilling sites. This shortcoming is linked to small spatial scales, both in horizontal and vertical directions, featuring a complex flow field and strong spatial variability in surface net snow accumulation rate. As a consequence, the uncertainties in the age/depth distributions of Alpine ice cores become substantial beyond the age of ∼100 years (Reference Wagenbach, Haeberli and StaufferWagenbach, 1994).
In the European Alps, Colle Gnifetti (CG) in the Monte Rosa summit range at 4500 m a.s.l. stands out as characterized by an extremely low net snow accumulation, in the range of only 15–50 cm w.e.a−1. Hence, in principle, CG offers ice-core records reaching far beyond the instrumental era. However, the preservation of fresh snow varies strongly with season at this site, leading to depositional noise. This effect is particularly significant because of the relatively weak long-term trends expected for the water isotope signal or the pre-industrial aerosol load (Reference Wagenbach, Bohleber and PreunkertWagenbach and others, 2012). Our ongoing multi-core approach aims to tackle the depositional noise problem at this drilling site by investigating the extent to which a common atmospheric signal is seen among four deep cores. For this purpose, it is necessary to know the internal layering of isochronous surfaces within the drilling place and to demonstrate that the age/depth distributions obtained at the four drilling sites are consistent with that structure.
Isochronous layering in ice sheets and glaciers is commonly investigated using ground-penetrating radar (GPR) to map the isochrone structure via the internal stratigraphy. At polar sites, spatial extrapolation of core ages using GPR has been carried out, for example, on the large ice sheets (Reference EisenEisen and others, 2008). The combination of GPR and flow modeling for this purpose has been established (e.g. in North Greenland (Reference Fahnestock, Abdalati, Luo and GogineniFahnestock and others, 2001), at Ridge B, Antarctica (Reference Leysinger Vieli, Siegert and PayneLeysinger Vieli and others, 2004) and at Taylor Mouth, Antarctica (Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others, 2007)).
Three of our four CG cores lie on a common flowline, yielding a two-dimensional (2-D) problem investigated by Reference Eisen, Nixdorf, Keck and WagenbachEisen and others (2003), who linked the glacio-chemical stratigraphy and age/depth relations of two ice cores by GPR reflectors. The additional drilling of the fourth core on a different flowline in 2005 makes the problem 3-D.
GPR data obtained from glaciers and ice sheets typically feature an echo-free zone (EFZ) near the bedrock, resulting from different physical causes at polar and Alpine sites. As acidity and density anomalies are the main cause of internal reflections, Reference Eisen, Nixdorf, Keck and WagenbachEisen and others (2003) connected the EFZ on CG (comprising the lower 50% of the ice thickness) to the firn/ice transition and a change in ice matrix chemistry to slightly alkaline. Consequently, the investigation of the internal stratigraphy by GPR is limited to the upper firn which typically covers only a few decades.
As a result, mapping the internal age distribution at the CG drilling area comprises the twofold task of extrapolating age information among the cores in the horizontal as well as the vertical. Here we attempt to tackle this challenge in a combined approach, based on age information from ice cores, GPR and a relatively simple flow model.
1.1. Site description
Among the extensively investigated Alpine drilling sites Col du Dôme (Mont Blanc area; Reference Vincent, Vallon, Pinglot, Funk and ReynaudVincent and others, 1997; Reference Preunkert, Wagenbach, Legrand and VincentPreunkert and others, 2000), Fiescherhorn (Bernese Alps; Reference Schwerzmann, Funk, Blatter, Lüthi, Schwikowski and PalmerSchwerzmann and others, 2006) and Colle Gnifetti, CG stands out as having a low net snow accumulation rate as a result of wind-driven snow erosion. The timescale covered by ice cores from CG thus comprises several centuries. Investigations that mainly address the glaciological features of the drill sites are reported by Reference Haeberli and AleanHaeberli and Alean (1985), Reference Haeberli, Schmid and WagenbachHaeberli and others (1988), Reference Eisen, Nixdorf, Keck and WagenbachEisen and others (2003) and Reference SchwerzmannSchwerzmann (2006). GPR measurements showed that ice thickness is up to 140 m (Reference Haeberli, Schmid and WagenbachHaeberli and others, 1988; Reference WagnerWagner, 1996; Reference LüthiLüthi, 2000; Reference Eisen, Nixdorf, Keck and WagenbachEisen and others, 2003). Surface velocity observations are reported by Reference Lüthi and FunkLüthi and Funk (2000), showing the typical diverging pattern related to the saddle geometry of CG and ranging from ∼0.6 to ∼4.5 m a−1 (fig. 11 of Reference Lüthi and FunkLüthi and Funk, 2000). Geodetic surveys and photogrammetric comparisons suggest that the glacier has been close to steady state in the 20th century (Reference WagnerWagner, 1996; Reference LüthiLüthi, 2000). The net surface accumulation rates range between 15 cm w.e.a−1 downwind of the south–north flow divide and 50 cm w.e.a−1 near the saddle point (Reference Alean, Haeberli and SchädlerAlean and others, 1983). The englacial temperature distribution is characterized by typically −14 to −10°C at 20 m depth and −13 to −12° C at bedrock (Reference Hoelzle, Darms, Lüthi and SuterHoelzle and others, 2011), which ensures preservation of the stratigraphy over the entire depth range. As CG falls into the recrystallization/infiltration zone classification (Reference ShumskiyShumskiy, 1964), melt layers typically a few centimeters thick form occasionally.
1.2. Location of ice cores and GPR profiles
The four CG ice cores which are linked in this study were drilled between 1982 and 2005. Cores CC and KCH are situated at the slope, and cores KCS and KCI at the saddle (Fig. 1). Cores KCH, CC and KCS are approximately situated on the same surface flowline (F1 in Fig. 1). GPR measurements along this flowline were performed in 2000 and were discussed by Reference Eisen, Nixdorf, Keck and WagenbachEisen and others (2003).

Fig. 1. Left: Locations of ice cores, GPR profiles and additional flowlines for model application on Colle Gnifetti (CG) within the studied area. North is downwards to match the photography. Surface topography is interpolated from GPS measurements. Center bottom: CG (white dot) in the European Alps (adapted from Reference Eisen, Nixdorf, Keck and WagenbachEisen and others, 2003). Right: View from Zumsteinspitze towards Signalkuppe –the two Monte Rosa summits enclosing CG – including the locations of GPR profiles and ice cores. The positions of ice cores, GPR profiles and bergschrund are only approximate.
The remaining core location, KCI, was chosen to be in a region featuring the exceptionally low net accumulation of ∼1−15 cm w.e. a−1 (Reference BöhlertBöhlert, 2005). The corresponding flowline, F5, originates in the same source region as F1, on the slope of Signalkuppe.
In 2008, further GPR profiles were recorded: two profiles along the KCI flowline (F4, F5) with slightly different courses; and two transverse profiles, one of them connecting KCH with the KCI flowline (T1) and one directly connecting the saddle cores KCI and KCS (T3). In 2010, two further flowlineparallel profiles (F2, F3) and one transverse profile (T2) were measured within the area defined by the former profiles, in order to increase the data density in this region.
1.3. Conceptual outline
The central goal for assessing the four age/depth distributions at the core locations against each other is to map the firn and ice stratigraphy within the drilling area. Based on the results of Reference Eisen, Nixdorf, Keck and WagenbachEisen and others (2003), who showed that comparison of the age/depth distributions along a single profile worked well within the depth range of GPR, we perform three steps:
-
1. Examine whether a consistent extrapolation of ice-core ages works on a larger number of GPR profiles, now within the array of the four cores.
-
2. Extend the age exploration laterally to map isochronous surfaces within the drilling area.
-
3. Possibly extend the investigation to older ages beyond the firn/ice transition which are inaccessible by GPR.
For this purpose, a simple 2-D flow model which accounts for lateral flow divergence was applied in order to increase the data density on isochronous surfaces (issue 2) and to overcome the depth limitation of GPR (issue 3). Starting from the code originally developed by Reference Vincent, Vallon, Pinglot, Funk and ReynaudVincent and others (1997), the flow model developed here is, in principle, based on the assumption of steady state, Glen’s flow law, 2-D geometry and mass-balance considerations. We did not use a more sophisticated model, such as a 3-D finite-element full Stokes code (Reference WagnerWagner, 1996; Reference LüthiLüthi, 2000), for the sake of efficiency and because of the pilot-study character of our investigation. The validation of the modeled isochrones was carried out by comparing them with isochronous reflectors that were tracked in the radargrams. Having interpolated the output isochroneś altitude, the results show that the age/depth distribution can be spatially extended by this approach, but absolute dating capabilities are limited. Nevertheless, the obtained isochronous layer architecture improves ice-core interpretation, especially as particle trajectories to the ice cores can be reconstructed to pin down their deposition location and, in turn, apply isotopic upstream corrections.
2. Data and Methods
2.1. GPR and ice cores
A combination of different dating methods has to be used to establish the chronologies of the CG ice cores. The datings are based on counting remnant seasonal cycles in impurities combined with absolute time horizons (e.g. the 1963 tritium peak and the large Saharan dust deposits in 1977, 1947 and 1901). For KCH, CC and KCS, annual-layer counting was performed in profiles of ionic impurities, especially relying on ammonium, as it provides the largest summer/winter contrast (Reference Preunkert, Wagenbach, Legrand and VincentPreunkert and others, 2000). An overview of dating these three cores is given by Reference Eisen, Nixdorf, Keck and WagenbachEisen and others (2003). In the low-accumulation KCI core, identification of annual cycles was mainly based on combining continuous flow analyses of mineral dust and electrical meltwater conductivity at centimeter depth resolution, backed up with the density profile measured at sub-centimeter resolution using γ-attenuation (Reference WilhelmsWilhelms, 1996). The same density-measuring technique was used for KCH and KCS; the density of CC was measured gravi metrically. Within the last 120 years the maximum dating uncertainty for all cores was estimated to be less than 3 to 5 years. The core characteristics are listed in Table 1.
Table 1. Characteristic parameters of the CG ice cores. Note the exceptionally low surface accumulation of KCI. Core depths marked with an asterisk indicate that a small amount of basal ice above bedrock may not have been recovered by the ice-core drilling. The maximum reaches are the depth values of the deepest consistent isochrones based on the results of our study

The general principle of the GPR method is to direct an electromagnetic signal into the ground and record the reflected parts of the signal as a function of two-way travel time (TWT). These reflections occur when the signal passes gradients of the dielectric properties (Reference Navarro, Eisen, Pellikka and ReesNavarro and Eisen, 2009).
The GPR data used in this study were obtained from measurements in common offset set-up, i.e. transmitter and receiver are kept at a fixed distance while being moved over the glacier surface with a shielded 250MHz antenna RAMAC GPR system. Technical details of the records are given in Table 2.
Table 2. Designation and properties of the GPR profiles. The trace distance is the distance between two shots. The signal-to-noise ratio is increased by vertical trace stacking of eight shots, or thirty-two in the case of F1, each consisting of 2048 samples in the 1.5μs long time window

The obtained data were processed routinely with Paradigm Geophysical’s FOCUS software, including static correction, bandpass filter, gain correction, 2-D migration and identification and tracking of prominent internal reflection horizons (IRHs) and bedrock reflection. Continuous reflectors observed in GPR data of the firn body of an alpine glacier mainly originate from layers with varying density (Reference Navarro, Eisen, Pellikka and ReesNavarro and Eisen, 2009). Since most of them are expected to come from short and instantaneous melting and refreezing events, they can be considered as isochrones. These reflectors, or the corresponding phases in the radargram, were tracked by eye. For the conversion of TWTs of each IRH to depth, a depth-dependent wave-speed distribution is necessary. Reference Kovacs, Gow and MoreyKovacs and others (1995) established the empirically obtained parameterization of the real part of the permittivity, ε′,as a function of density, ρ:

Using Eqn (1), the wave speed, v = c
0/√ε′ (with c
0 the speed of light in a vacuum) can be obtained from a density estimation over the whole area of interest. The edges of GPR profiles parallel to flowlines were specified as ‘slope’ or ‘saddle’ locations, between which the characteristic smoothed density profiles obtained from the ice cores were interpolated linearly with horizontal distance for given values of relative depth, Σ = z/H, with depth, z, and ice thickness, H. By this means, an average density distribution could, in principle, be estimated at any location within the array. The TWT of the bedrock reflection, ![]() , at a given horizontal position can be converted into the corresponding ice thickness by
, at a given horizontal position can be converted into the corresponding ice thickness by
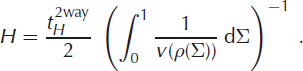
Afterwards, the interpolated density distribution can be considered as a function of depth instead of relative depth, and the conversion of TWTs to depth z is
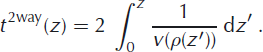
Two ice-core chronologies can be compared by evaluating the age/depth relations of the two cores at the respective depth of an IRH in a radargram of a profile that connects these two cores. A potential misfit of the resulting two ages is then either due to the inadequate assumption of isochronous layers in the radargram, to inconsistent age/depth relations of the compared cores or to inadequate processing of the GPR data (e.g. over- or under-migration, conversion from TWT to depth or phase picking). Additionally, off-plane reflections and off-profile tilt of the reflecting surface could not be treated, due to the nature of 2-D data acquisition and processing. The comparison of ice-core timescales using GPR profiles where data were obtained at different times requires two conditions to be fulfilled: first, use of relative age scales with respect to the surface, where age is zero; and second, steady-state conditions, which imply that the relative age/depth relation at any location, and thus the internal layer architecture (i.e. shape), does not vary in time. Following the introductory indication of a steady state on CG, we assume that the comparison may be carried out referring to any time. But, for the sake of clarity, we fix 2010 as the reference time, i.e. 2010 ≙ 0 years BP. The comparison of the three cores, KCH, KCS and KCI, was carried out as described above on various reflectors. Since the CC drilling site is not located directly on the GPR profile F1, it is not considered at this stage.
The next step is to not only compare two cores at a time but all four at once. Layers were tracked along the different profiles and checked for consistent TWTs, or depths, at the intersections of the profiles. Eleven phases of distinct reflectors in the radargrams were picked on each profile, starting at the intersection with a previously treated profile which featured the deeper location of the considered layer, in order to avoid ambiguities from changing phase patterns of neighboring reflectors. A typical illustration of these 11 horizons is shown in Figure 2 for profile T3, which connects the two saddle cores KCI and KCS. By dating these layers using the age/depth relations of the cores, we obtained preliminary, coarsely gridded information on isochronous surfaces.

Fig. 2. Center: Migrated radargram of the profile connecting KCI and KCS (T3 in Fig. 1). The selected GPR signal phases and the bedrock reflection are illustrated in black. Note the strong ambiguity of the latter; the actual course of the picked bedrock resulted from the strongest reflections in the radargram, which were identified after decreasing gain. Left: zoom to KCI. Right: zoom to KCS. Note that prominent reflectors in the zoomed regions are not picked because they are not as prominent along the whole profile or along the other profiles. In the center panel, every second horizon is left out, in order to improve the overview.
2.2. Flow modeling
Primarily aimed at calculating a 2-D velocity field, the model input data are flowline-related and comprise surface and bedrock topography, the net accumulation rate distribution (mw.e. a−1) and two vertical density profiles, typically located at the start and end points of the flowline. All input data refer to a fixed global reference frame. Using interpolated density/depth data, the glacier thickness is converted into water-equivalent depth. For sections with piecewise-linearized surface and bedrock topographies, the model uses a local reference frame where the surface-parallel axis, x, is positive downslope and the z-axis points downwards perpendicular to the surface. From Glen’s flow law with an exponent of n = 3, one obtains the analytical solutions for the velocity components parallel and perpendicular to the surface, u(x, z) and w(x, z), respectively (Reference LliboutryLliboutry, 1979; Reference RitzRitz, 1987; Reference Vincent, Vallon, Pinglot, Funk and ReynaudVincent and others, 1997). At this stage, we consider the model domain to consist of pure ice, through conversion into water equivalent. Unlike Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier (1997) and Reference LüthiLüthi (2000) we thus neglect any firn rheology, using
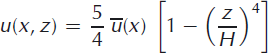

Here ![]() is net surface accumulation and
is net surface accumulation and ![]() is the depth-averaged horizonal velocity. The latter is calculated from a 2-D mass balance, based on equality of accumulated mass upstream from position x (right-hand side of Eqn (6)) and flow through unit area at x (left-hand side of Eqn (6)) in steady state:
is the depth-averaged horizonal velocity. The latter is calculated from a 2-D mass balance, based on equality of accumulated mass upstream from position x (right-hand side of Eqn (6)) and flow through unit area at x (left-hand side of Eqn (6)) in steady state:

Parameter q 0 accounts for potential inflow of ice at the flowline’s upper boundary, x = 0. The divergence parameter, D, accounts for the transversal flux divergence due to otherwise neglected transversal velocity components. For conversion from water equivalent into absolute length rate (m a−1), u and w are scaled according to the local relative density, i.e ρ water/ρ local. Since the velocity component perpendicular to bedrock must vanish at the glacier bed, the kinematic correction, Δw, is subtracted from w:
The adoption of the above equations to the piecewiselinearized flowline geometry makes it necessary to use vertical depth from the surface instead of the surface-normal coordinate, z, and vertical ice thickness, H, in these equations. According to the polynomial structure, the effect of this substitution is negligible in the upper regions of a flowline. This simplification leaves u and w in the local reference frame, such that they have to be transferred to the global reference frame (index 0) by applying a respective rotation matrix. Based on the 2-D velocity profile, the model computes particle trajectories, x 0, z 0, in discrete steps, k, corresponding to a time interval of Δt = 1 year:
The respective particle age since deposition is obtained according to t (k+1) = t (k) + Δt, allowing simulation of isochronous layers within the suitable model domain.
Probably the most inadequate simplifications of this model with respect to modeling an alpine glacier are to consider only a 2-D flow field and stationary input fields, and to neglect a firn rheology, which will lead to results deviating from observations (e.g. ice-core chronologies). In order to take into account the input quantities’ uncertainty and variability (the latter especially in the case of the surface accumulation rate) a sensitivity study concerning the isochrone patterns was performed, revealing that:
-
the shape of the spatial accumulation-rate pattern determines the shape of the isochrones in the firn layer, as it directly corresponds to the surface-normal velocity component, w, near the surface;
-
the exact vertical location of an isochrone is fixed by the absolute values of the accumulation-rate distribution and the density input due to the scaling;
-
the influence of the bedrock topography due to the basal boundary condition is limited to the deeper parts and
-
the influence of the flux parameters, D and q 0, on the vertical velocity component, and therefore on the isochrones, is negligible compared with the sensitivities listed above.
To estimate the propagation of input uncertainty, a routine for sampling-based uncertainty analysis was developed as an add-on to the flow model. It runs the model a defined number of times (usually 500) and applies input parameters randomly varied in a Gaussian distribution within the range of their uncertainty. The mean altitude of the isochrones and its standard deviation are then calculated from the various model run outputs.
2.3. Model-assisted age exploration
Surface topography along the GPR profiles was available from GPS measurements in 2008 and 2010. Bedrock topography could be inferred from the picked bedrock reflections in the radargrams. In this procedure, one typically tends to underestimate the ice thickness, due to surface/bed inclination, which limits the accuracy of the GPR data to at best 2m (Reference Eisen, Nixdorf, Keck and WagenbachEisen and others, 2003). With the array’s coverage by GPR profiles being too coarse for 3-D migration, we cannot expect ice thickness to be more accurate than ∼16% where the bedrock is strongly inclined (Reference Moran, Greenfield, Arcone and DelaneyMoran and others, 2000). The accumulation rate along the GPR profiles could be obtained by dating the tracked isochronous layers using the age/depth relations of the ice cores. Annual-layer thinning was considered, by applying Nye’s timescale (Reference Cuffey and PatersonCuffey and Paterson, 2010) as a first-order approximation and averaging accumulation rate from all available consistent IRHs (Section 3).
By interpolating these input quantities to a greater area including the ice cores and GPR profiles, the model was applicable not only to the five flowlines defined by the flowline-parallel GPR profiles, but also to 11 further profiles defined roughly via the surface altitude gradient (Fig. 1), amounting to a total of 16 flowlines. We chose ordinary kriging for the spatial interpolation of the input data, a well-established method in alpine glaciology (Reference Herzfeld, Eriksson and HolmlundHerzfeld and others, 1993), because surface splines and polynomial interpolation lead to physically unreasonable artifacts. The interpolation was carried out on a 1m × 1m grid.
The density input was chosen equivalent to the density estimation in the TWT/depth conversion routine. The influx, ![]() , at the model’s upper edge of the flowlines could be estimated from the distance, Δx, to the bergschrund, where we assume zero downhill mass flux, and the mean accumulation rate,
, at the model’s upper edge of the flowlines could be estimated from the distance, Δx, to the bergschrund, where we assume zero downhill mass flux, and the mean accumulation rate, ![]() , near the bergschrund downhill from Signalkuppe. (The bergschrund location is indicated in Fig. 1.) The divergence parameter, D, was estimated globally from fits to surface velocity measurements reported by Reference Lüthi and FunkLüthi and Funk (2000), i.e. one value for all flowlines.
, near the bergschrund downhill from Signalkuppe. (The bergschrund location is indicated in Fig. 1.) The divergence parameter, D, was estimated globally from fits to surface velocity measurements reported by Reference Lüthi and FunkLüthi and Funk (2000), i.e. one value for all flowlines.
Having applied the model to the 16 flowlines, the isochrone altitude along the different flowlines was interpolated spatially for various model ages, again by ordinary kriging. Thus, we obtained the coordinates for isochronous surfaces within the area of interest.
3. Results and Discussion
3.1. GPR and ice cores
The pairwise comparison of ice cores is shown in Figure 3. The only systematic discrepancies are (1) the tendency towards higher KCH ages compared to KCI and KCS and (2) a mismatch of 40–50 years bp KCI age in the KCI/KCS comparison. Up to 60 years bp, various continuous reflectors could be tracked. For greater ages, only a few reflectors could be found, so the data density becomes much lower and the comparison is limited to ∼80 years bp. Most of the illustrated ages agree within the uncertainty range of 3–5 years (Section 3.4), and those few that do not are still close to the respective bisecting line. Thus, the presented pairwise comparison of the cores works up to 60 years bp in general and to 80 years bp between single core pairs.

Fig. 3. Pairwise comparison of core ages from KCI, KCH and KCS via GPR layers. For each distinct phase traceable in the GPR profile linking the respective drilling sites, ages are assigned according to each ice-core dating. Ideal agreement is given if the data points are situated on the bisecting line.
Since the GPR profiles were recorded within a time-span of 10 years, the picked TWTs in two different radargrams at their intersection do not correspond to the same reflector and physical origin. Therefore, it is not, a priori, given that the core ages are consistent when all available profiles are considered at the same time. However, the upper eight of the eleven IRHs, which were tracked on the closed course, agree well at the profile intersections. At all intersections the discrepancy of the picked TWTs on each pair of profiles is not more than 20 ns, roughly corresponding to a depth interval of 1.8m. At the core locations the ages of the reflectors agree within the specific uncertainty range (Table 3). At greater ages, the discrepancy between IRH travel times from different profiles increases mainly near KCI.
Table 3. IRH ages of the reflections tracked on the closed course (yearsbp). The uncertainty of the ages of IRH numbers 1–8 varies in the range 3.1–5.2 years. For IRH numbers 9–11, the range is 4.1–11.6 years. Note that these IRHs were rejected. The last column contains the ages assigned to the consistent IRHs obtained as the average of KCS and KCI ages from T3, except for IRH number 5, where there is a preference for KCS. Discrepancies in the arithmetical average of columns 3 and 4 result from rounding

We can thus conclude that the age consistency on the closed course is given up to ∼50years BP. Consequently, the three deepest IRHs were rejected due to their lack of consistency at KCI. Profile T2 was rejected completely in this analysis because the tracked layers were highly inconsistent at the intersections, most likely due to the high trace distance (Table 2) yielding large systematic errors in phase tracking.
For further processing of the data, namely accumulation-rate computation and validation of the model isochrones via GPR isochrones, unique ages of the remaining eight IRHs had to be determined from the various core ages (Table 3). This was challenged by the tendency to higher ages for KCH compared with the other cores. Since the picked TWTs of the isochronous layers are consistent at KCH, this tendency does not imply inconsistency of the layers. We chose to average the KCI and KCS ages from T3 for layer dating because of their high consistency. On IRH 5, where there is a relatively large discrepancy of KCS and KCI age on T3, the KCS age was preferred because the KCI age is implausibly low.
3.2. Modeled vs GPR isochrones
We assessed the modeled isochrones by comparing them with the GPR isochrones on those flowlines for which GPR data are available. As an example, the comparison is shown for flowlines F1 (from KCH to KCS) and F3 in Figure 4. The general shape of the GPR isochrones is reproduced by the model. However, the exact depth differs by up to 3.5 m. The mismatch in depth is directly related to the model’s incapability to date an ice core. The agreement in shape is attributed to the accumulation-rate input, which governs the shape of the isochrones in the respective shallow-depth range and which is directly obtained from the GPR isochrones. We conclude that we can use the model output for lateral and vertical isochrone extension, but have to assign ice-core ages to the modeled and interpolated isochronous surfaces, which strongly differ from the modeled ages. This is an expected consequence of the model’s simplicity and means that the model cannot be used for ice-core dating on its own.

Fig. 4. Comparison of GPR isochrones and model isochrones on flowlines F1 (left) and F3 (right). On F1 there are parts in which GPR and model isochrones do not agree within the 1σ range of uncertainty. On F3 the GPR and model isochrones agree well within the 1σ range of uncertainty. The isochrones’ ages are, from top to bottom, 11, 19, 29 and 44 years BP.
3.3. Model-assisted extension of the age distribution
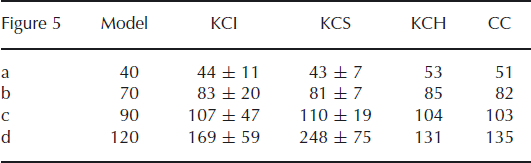
The interpolated surfaces of four modeled isochrones are illustrated in Figure 5. Apart from the contour distortion near KCS, no systematic artifact appears in the interpolated isochrones. At greater ages, however, further distortions appear near the eastern edge of the studied array. They are most likely due to the interpolation and possibly due to the model input, which can be inconsistent on adjacent flowlines. Nevertheless, apart from the mentioned features, the resulting isochrones appear reasonable and thus are assumed to represent the spatial age distribution down to a certain depth in the studied area.

Fig. 5. Spatially interpolated isochrones based on the flow model tied to GPR and ice-core data (core ages are given in Table 4). Top row: altitude; bottom row: depth. Note the contour distortions near KCS appearing in all plots. With increasing age, the altitude surfaces migrate from a pattern similar to the glacier surface (Fig. 1), indicating a smooth representation of the flow field (a) to a disturbed and rough pattern (d). Note: north direction is upwards here, i.e. opposite to Figure 1.
The age/depth distributions of the four cores are considered for assigning real ages to the modeled and interpolated isochrones. This allows us to assess the isochronous characteristics of the interpolated surfaces (Fig. 6, bottom). Up to ages of ∼110 years bp, the values assigned to the isochronous surfaces according to the individual ice-core datings lie along the bisecting line, thus revealing age consistency for the respective surface. At ages >110 years BP, the relation between the individual datings remains linear, deviating however from the bisecting line (see further dashed lines with slope <1 in Fig. 6, bottom). Nevertheless, CC and KCH ages clearly fit together well.

Fig. 6. Bottom: Comparison of KCI, KCH and CC ages to KCS ages via the modeled and interpolated isochrones. Note that KCI tends to younger ages than KCS and that in the case of KCH and CC this effect is even more pronounced. Four of these data points correspond to the surfaces illustrated in Figure 5. Top: icecore-based vs modeled KCS dating. The ice-core-based age/depth relation features a characteristic bend which does not appear in the model dating.
Table 4. Comparison of core ages (years bp) of the isochrones illustrated in Figure 5. KCH and CC ages are given without uncertainty because of their upstream location, where the propagation of uncertainty in the model cannot be computed
We note that the occurrence of the deviating age trends coincides with the characteristic bend in the KCS age/depth distribution (Fig. 6, top), most likely because of decreasing surface accumulation upstream of KCS. The depth of this bend is not equal to that of the firn/ice transition. The KCS age/depth distribution calculated by the model based on the accumulation-rate pattern derived from GPR is much more analytical, hence lacking the distinct bend (Fig. 6, top). We investigated whether the bend can be reproduced by the model and found that this is only possible if the accumulation-rate pattern is decreased by ∼80% to just 5 cmw.e.a−1 along 150m of the KCS flowline, which makes up 75% of the whole modeled flowline, and then increases to 60cmw.e.a−1 within just 40 m.
This extreme boundary condition, which does not represent the mean accumulation conditions of the last ∼80 years BP as derived from the GPR data, leads to the conclusion that the isochrone mapping beyond 110 years BP suffers, at least in the vicinity of KCS, where two main problems occur at the same time: (1) the upstream effect and (2) the poor 2-D representation of the situation (the bed slope strongly varies from the flowline direction). This is expected to induce lateral divergence which is not taken into account by applying the divergence parameter, D. Further contributions could also arise from changes in viscosity due to changes with depth in flow regime, mechanical properties such as damage, or material properties such as density and fabric. However, at the current stage it is difficult to quantify the contribution of these effects. We suggest that they are rather small compared with the points discussed above.
Obviously, the ice flow near KCS is not the only limiting aspect. The ages from the three remaining cores do not only differ from the KCS ages. The KCI ages show a different trend to those from the two slope cores. In contrast to KCS and KCI, the slope cores feature relatively analytical age/depth distributions, and the modeled 2-D flow is expected to be a good representation because of the short distance between the two cores and because lateral effects are only small at the slope. This might be why the ages from these two cores fit together very well, while they do not fit well with the saddle cores. As stated above, another shortcoming of the model is that it only accounts for stationary input, especially accumulation conditions, which might also affect the consistency of the ages from the different cores. Nevertheless, the interpolated surfaces at ages less than 110 years BP can be assumed to be isochronous.
3.4. Measurement and modeling uncertainties
The spatial extension of the transmitted radar signal and the uncertainty of the density distribution via the wave speed distribution obtained from Eqn (1) restrict the identification of internal reflector depth to ∼0.5–0.8m or 3–5 years at ages younger than 80 years BP. The uncertainty in the model isochrones’ depth coordinates is obtained using the uncertainty propagation routine. It increases towards the bedrock and downstream. With values in the range 0.9–3m or 2–27 years at ages less than 120 year BP it is generally greater than the depth uncertainty of the GPR (Fig. 4). As the isochrones are most sensitive to the accumulation-rate input, the accumulation rate is assumed to be dominant for isochrone depth uncertainty.
The errors in the ages assigned to the modeled isochrones are composites of the uncertainty of the age/depth distribution and the uncertainty in isochrone depth from the propagation of model input uncertainty. While the former increases from 3 years to a maximum of 20years at the maximum illustrated age of 232years BP or 27 m (17.4mw.e.) core depth at KCI, the latter is dominant, due to the relatively large depth uncertainty via the age/depth distribution gradients. The error in the KCI and KCS ages increases from 7 to 80 years, and to >100 years in the case of KCS ages older than 300 years BP. In the range where the trends in the age comparison are not yet apparent and where our results are thus assumed adequate, namely at ages <110 years BP, the errors amount to a maximum of 47 years at KCI and 19 years at KCS.
Since KCH and CC are situated too far upstream for an estimate of depth uncertainty via the uncertainty propagation within the model runs, and these are expected to be dominant for the respective age uncertainty, we exclude the age uncertainties of these two cores. The large uncertainty intervals might yield agreement of the different core ages even for greater ages. However, the trends starting at 110 years BP illustrate the limit of age extrapolation to greater depth by this method.
3.5. Evaluation of the method
The approach presented here demonstrates reasonable age coherency among the CG ice cores within at least the past 110 years. The substantial depth and age limitations remain a major issue and need to be addressed in order to continue the promising approach developed here at greater depths. Since distinct changes in density vanish beyond the firn/ice transition, acidity variations are left as the prime reflection mechanism. As pointed out by Reference Eisen, Nixdorf, Keck and WagenbachEisen and others (2003), the chemical composition of the ice changes from acidic to slightly alkaline prior to 1950 (fig. 4 of Reference Eisen, Nixdorf, Keck and WagenbachEisen and others, 2003) and thus above the firn/ice transition in all cores. Below that, pronounced acidity peaks are hardly detected. In addition, the annual-layer thickness below the firn/ice transition is typically in the order of only a few centimeters for the CG ice cores. With the GPR wavelength far exceeding this magnitude, this contributes to a reduced effective reflectivity of a potentially reflecting horizon. Altogether, the disappearance of strong density variations seems to coincide at a critical depth with the presence of an alkaline background and small annual layers. The result is a distinct decrease in overall reflection coefficient and hence in the amount of energy reflected to the surface. Sophisticated GPR deployment may contribute to a technical solution for detecting reflections below the firn/ice transition. For example, an increase in signal-to-noise ratio could be obtained by means of high horizontal resolution in additional common offset profiles while stacking a large number of shots (>100). Additional information may be obtained using broadband systems, such as stepped frequency or frequency-modulated continuous wave. As has recently been shown for Antarctica and Greenland, the use of phased-array antennas in the lateral direction to the measured profile can reduce clutter. As these approaches are either very time-consuming or require heavy logistic support, they have not yet been deployed. Previous field campaigns were mainly dedicated to obtaining extended spatial coverage. Consequently, overcoming the depth limitation of GPR IRHs at CG was not the focus of the present study. Nevertheless, application of improved radar techniques on CG remains an issue in the medium term.
At CG, full 3-D flow modeling using a modified flow law accounting for the deformational behavior of the large firn fraction (Reference LüthiLüthi, 2000) has been found equally inconsistent with the ice-core-based age/depth relations (Reference ArmbrusterArmbruster, 2000). Hence, when considering greater depths where GPR IRHs are absent, flow models in combination with uncertain and/or possibly temporally varying input fields certainly become most deficient close to the bedrock, due to their fundamental inadequacy in representing the large spatio-temporal variability at CG. As a consequence of the depth limits imposed on the use of flow models and GPR to provide reliable age estimates at greater depths, further age information must come from ice cores. Here observational age constraints provided by sophisticated radiometric dating methods seem most promising. Although potentially influenced by production and reservoir effects, radiocarbon dating of particulate carbon has been used to constrain the age of the lowest ice at CG (Reference JenkJenk and others, 2009; Reference MayMay, 2009). If two ice cores with thereby improved chronologies exist, the approach presented here provides the opportunity for matching, for example when connected to some undated outstanding feature in the ice-core profiles, thus substituting for the missing IRHs.
As illustrated in Figure 5, the combined approach presented here reveals the first comprehensive picture of isochrone layering within the drilling area at CG. The approach successfully facilitates the spatial interpolation of age information, although restricted to approximately the upper half of the glacier thickness for highest accuracy.
The application of our combined approach to other drilling sites requires at least the presence of a single dated ice core as well as reasonably dense spatial coverage by GPR profiles. The number of ice cores and GPR profiles necessary for a successful application depends on the complexity of the site, i.e. the scale and sampling trait. Small-scale high alpine drilling sites might profit from an investigation of the internal age distribution with the combined approach presented here. Dating ice cores over a few hundred years is typically regarded as less of a challenge for larger ice bodies, such as ice caps in the Arctic (Reference FisherFisher and others, 1998) and at lower latitudes (Reference ThompsonThompson and others, 1993). Here the spatial extrapolation of ice properties other than age might appear more interesting, for which the combined approach may be readily adapted.
4. Conclusion and Outlook
The present study demonstrates a decadal to centennial degree of consistency of CG ice-core ages. Our ice-core synchronization provides accurate isochrone surfaces for selected ages of 50, 80 and 110 years BP, depending on specific combinations of data and methods, despite the large age uncertainty when considering the interpolated model results. The reasonably validated model produces particle trajectories which form the basis for correction of ice-core quantities for upstream effects in future work. The multi-core approach for deciphering the common climate history might benefit especially from upstream corrections, individually applied to each core.
Our analysis produces the first estimates of upstream trajectories for the KCI ice core. It thus spatially and methodologically complements earlier approaches to compute backward trajectories for the KCS ice core (Reference LüthiLüthi, 2000). Nevertheless, our method’s limitations and accompanying uncertainties underline the difficulty in exploring the age consistency at greater depths, i.e. in the lower 50% of the firn/ice column.
Future enhancements to all three stand-alone components presented here might yield results reaching beyond the present limitations. Firstly, although a more sophisticated flow model (e.g. Reference LüthiLüthi, 2000) including a firn rheology might improve results for the deeper layers when using our extended bedrock topography, problems with data coverage, especially of flow velocities at the surface, will continue to limit the calibration and validation of the model. Area-wide coverage could be obtained from imaging synthetic aperture radar or repeated high-resolution visible imagery for speckle tracking, from satellites or airplanes, or deployed on adjacent summits (e.g. Zumsteinspitze). Extended data coverage is also necessary to include temporal and spatial variations in accumulation in future studies. Secondly, regarding ice-core analysis, the chronologies are subject to revisions, for example by 14C dating (Reference MayMay, 2009). Future findings on maximum or minimum ages at specific depths have the potential to provide further constraints for our method. Thirdly, although detection of deeper reflectors in GPR data was not possible at this stage, future applications of advanced radar techniques (e.g. phased arrays and synthetic aperture processing) could provide a more detailed picture at presently inaccessible depths.
In the analysis above, we ensured that the interpolated surfaces were isochrones within an acceptable uncertainty range. An obvious application is the distribution of further tracer quantities that are known from ice cores and expected to be preserved on isochronous surfaces, such as annual-layer characteristics (i.e. dust content and isotopes to some extent). Our method is a simple but useful tool for mapping and interpolating isochronous layers. However, because of the limitations, it is unable to provide absolute age/depth scales, which still have to be derived from an ice core. Since the determination of ages at great depths in Alpine ice cores remains a challenge, successful progress to greater ages will probably be limited, even with more sophisticated methodological compartments.
The transfer of our methods to other alpine or subpolar sites primarily demands a conserved internal stratigraphy in the infiltration/recrystallization regime, detectable by GPR applications, and a single dated ice core. However, the observed increasing warming of ice masses (e.g. at CG; Reference Hoelzle, Darms, Lüthi and SuterHoelzle and others, 2011) calls for data acquisition in the near future, before internal stratigraphy is disturbed by meltwater percolation.
Acknowledgements
We are grateful for invaluable logistic support by the staff of Cabanna Regina Margherita from the Club Alpino Italiano di Varallo/MBG Impresa, by Air Zermatt, from the High Altitude Research Stations Jungfraujoch and Gornergrat on Gornergrat, and for the cooperation of the Department of Geography, University of Zürich, in particular Martin Hoelzle and Ralph Böhlert. We acknowledge the generosity of Bernhard Stauffer and Thomas Stocker in lending us their dedicated drill equipment. We particularly thank chief driller Heinrich Rufli for his invaluable effort in all drilling campaigns. Financial support for this study was provided to O.E. by the Deutsche Forschungsgemeinschaft (DFG) ‘Emmy Noether’ program grant EI 672/5-1. P.B. acknowledges a completion grant from the University of Heidelberg Graduate Academy. Part of the study was funded by the European Union within the ALP-IMP project through grant EVK2-CT 2002-00148. We thank Reinhard Drews, Anja Diez and Coen Hofstede for their contributions during the campaigns. Additionally, we thank Reinhard Drews for his support in GPR data processing and Martin Lüthi for discussions and making data available. Finally, we thank two anonymous referees for helpful comments and suggestions.












