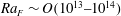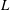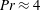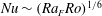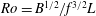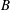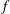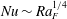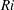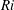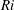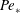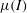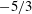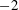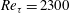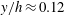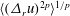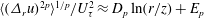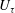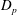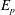Papers
Self-similarity of fluid residence time statistics in a turbulent round jet
-
- Published online by Cambridge University Press:
- 14 June 2017, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conditional sampling of a high Péclet number turbulent plume and the implications for entrainment
-
- Published online by Cambridge University Press:
- 15 June 2017, pp. 26-56
-
- Article
- Export citation
Geostrophic and chimney regimes in rotating horizontal convection with imposed heat flux
-
- Published online by Cambridge University Press:
- 15 June 2017, pp. 57-99
-
- Article
- Export citation
Effect of geometry and Reynolds number on the turbulent separated flow behind a bulge in a channel
-
- Published online by Cambridge University Press:
- 15 June 2017, pp. 100-133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multivariate and conditioned statistics of velocity and wall pressure fluctuations induced by a jet interacting with a flat plate
-
- Published online by Cambridge University Press:
- 15 June 2017, pp. 134-165
-
- Article
- Export citation
Stability and three-dimensional evolution of a transitional dynamic stall vortex
-
- Published online by Cambridge University Press:
- 15 June 2017, pp. 166-197
-
- Article
- Export citation
Diapycnal mixing in layered stratified plane Couette flow quantified in a tracer-based coordinate
-
- Published online by Cambridge University Press:
- 15 June 2017, pp. 198-229
-
- Article
- Export citation
Optimal sensor placement for variational data assimilation of unsteady flows past a rotationally oscillating cylinder
-
- Published online by Cambridge University Press:
- 16 June 2017, pp. 230-277
-
- Article
- Export citation
Formation of levees, troughs and elevated channels by avalanches on erodible slopes
-
- Published online by Cambridge University Press:
- 16 June 2017, pp. 278-315
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surfing surface gravity waves
-
- Published online by Cambridge University Press:
- 16 June 2017, pp. 316-328
-
- Article
- Export citation
Wind farm power fluctuations and spatial sampling of turbulent boundary layers
-
- Published online by Cambridge University Press:
- 16 June 2017, pp. 329-344
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformation of a compliant wall in a turbulent channel flow
-
- Published online by Cambridge University Press:
- 16 June 2017, pp. 345-390
-
- Article
- Export citation
Submesoscale surface fronts and filaments: secondary circulation, buoyancy flux, and frontogenesis
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 391-432
-
- Article
- Export citation
Clustering instabilities in sedimenting fluid–solid systems: critical assessment of kinetic-theory-based predictions using direct numerical simulation data
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 433-469
-
- Article
- Export citation
Evaporating pure, binary and ternary droplets: thermal effects and axial symmetry breaking
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 470-497
-
- Article
- Export citation
Universality of the energy-containing structures in wall-bounded turbulence
-
- Published online by Cambridge University Press:
- 21 June 2017, pp. 498-510
-
- Article
- Export citation
Assessment and development of the gas kinetic boundary condition for the Boltzmann equation
-
- Published online by Cambridge University Press:
- 21 June 2017, pp. 511-537
-
- Article
- Export citation
Shock transformation and hysteresis in underexpanded confined jets
-
- Published online by Cambridge University Press:
- 21 June 2017, pp. 538-561
-
- Article
- Export citation
Feedback loop and upwind-propagating waves in ideally expanded supersonic impinging round jets
-
- Published online by Cambridge University Press:
- 22 June 2017, pp. 562-591
-
- Article
- Export citation
Velocity fluctuations generated by the flow through a random array of spheres: a model of bubble-induced agitation
-
- Published online by Cambridge University Press:
- 22 June 2017, pp. 592-616
-
- Article
- Export citation