Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T08:30:28.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Using stratification to mitigate end effects in quasi-Keplerian Taylor–Couette flow

Published online by Cambridge University Press:  24 February 2016

Colin Leclercq Open the ORCID record for Colin Leclercq [Opens in a new window] ,
Jamie L. Partridge ,
Pierre Augier ,
Stuart B. Dalziel  and
Rich R. Kerswell
Colin Leclercq*
Affiliation:
School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, UK
Jamie L. Partridge
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Pierre Augier
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Stuart B. Dalziel
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Rich R. Kerswell
Affiliation:
School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, UK
*
†Email address for correspondence: c.leclercq@bristol.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Efforts to model accretion disks in the laboratory using Taylor–Couette flow apparatus are plagued with problems due to the substantial impact the end plates have on the flow. We explore the possibility of mitigating the influence of these end plates by imposing stable stratification in their vicinity. Numerical computations and experiments confirm the effectiveness of this strategy for restoring the axially homogeneous quasi-Keplerian solution in the unstratified equatorial part of the flow for sufficiently strong stratification and moderate layer thickness. If the rotation ratio is too large, however (e.g. 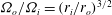${\it\Omega}_{o}/{\it\Omega}_{i}=(r_{i}/r_{o})^{3/2}$, where 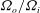${\it\Omega}_{o}/{\it\Omega}_{i}$ is the angular velocity at the outer/inner boundary and $r_{i}/r_{o}$ is the inner/outer radius), the presence of stratification can make the quasi-Keplerian flow susceptible to the stratorotational instability. Otherwise (e.g. for 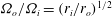${\it\Omega}_{o}/{\it\Omega}_{i}=(r_{i}/r_{o})^{1/2}$), our control strategy is successful in reinstating a linearly stable quasi-Keplerian flow away from the end plates. Experiments probing the nonlinear stability of this flow show only decay of initial finite-amplitude disturbances at a Reynolds number 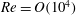$Re=O(10^{4})$. This observation is consistent with most recent computational (Ostilla-Mónico, et al.J. Fluid Mech., vol. 748, 2014, R3) and experimental results (Edlund & Ji, Phys. Rev. E, vol. 89, 2014, 021004) at high 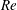$Re$, and reinforces the growing consensus that turbulence in cold accretion disks must rely on additional physics beyond that of incompressible hydrodynamics.

JFM classification

Flow Control: Flow Control Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 608 - 630
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abshagen, J., Heise, M., Pfister, G. & Mullin, T. 2010 Multiple localized states in centrifugally stable rotating flow. Phys. Fluids 22, 021702.Google Scholar
Avila, M. 2012 Stability and angular-momentum transport of fluid flows between corotating cylinders. Phys. Rev. Lett. 108, 124501.Google Scholar
Avila, M., Grimes, M., Lopez, J. M. & Marques, F. 2008 Global endwall effects on centrifugally stable flows. Phys. Fluids 20, 104104.Google Scholar
Balbus, S. A. 2011 Fluid dynamics: a turbulent matter. Nature 470, 475–476.Google Scholar
Balbus, S. A. & Hawley, J. F. 1991 A powerful local shear instability in weakly magnetized disks. 1. Linear analysis. Astrophys. J. 376, 214–222.CrossRefGoogle Scholar
Balbus, S. A. & Hawley, J. F. 1998 Instability, turbulence and enhanced transport in accretion disks. Rev. Mod. Phys. 70, 1–53.CrossRefGoogle Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Chandrasekhar, S. 1960 The stability of non-dissipative Couette flow in hydromagnetics. Proc. Natl Acad. Sci. USA 46, 253–257.CrossRefGoogle ScholarPubMed
Czarny, O., Serre, E., Bontoux, P. & Lueptow, R. M. 2003 Interaction between Ekman pumping and the centrifugal instability in Taylor–Couette flow. Phys. Fluids 15, 467–477.Google Scholar
Dalziel, S. B., Carr, M., Sveen, J. K. & Davies, P. A. 2007 Simultaneous synthetic Schlieren and PIV measurements for internal solitary waves. Meas. Sci. Technol. 18, 533–547.CrossRefGoogle Scholar
Dubrulle, B., Marié, L., Normand, C., Richard, D., Hersant, F. & Zahn, J.-P. 2005 A hydrodynamic shear instability in stratified disks. Astron. Astrophys. 429, 1–13.Google Scholar
Edlund, E. M. & Ji, H. 2014 Nonlinear stability of laboratory quasi-Keplerian flows. Phys. Rev. E 89, 021004.CrossRefGoogle ScholarPubMed
Hollerbach, R. & Fournier, A. 2004 End-effects in rapidly rotating cylindrical Taylor–Couette flow. In AIP Conference Proceedings, vol. 733, pp. 114–121.Google Scholar
Ji, H., Burin, M., Schartman, E. & Goodman, J. 2006 Hydrodynamic turbulence cannot transport angular momentum effectively in astrophysical disks. Nature 444, 343–346.Google Scholar
Le Bars, M. & Le Gal, P. 2007 Experimental analysis of the stratorotational instability in a cylindrical Couette flow. Phys. Rev. Lett. 99 (6), 064502.Google Scholar
Le Dizès, S. & Riedinger, X. 2010 The strato-rotational instability of Taylor–Couette and Keplerian flows. J. Fluid Mech. 660, 147–161.Google Scholar
Leclercq, C., Pier, B. & Scott, J. F. 2013 Temporal stability of eccentric Taylor–Couette–Poiseuille flow. J. Fluid Mech. 733, 68–99.Google Scholar
Lopez, J. M., Marques, F. & Avila, M. 2013 The Boussinesq approximation in rapidly rotating flows. J. Fluid Mech. 737, 56–77.CrossRefGoogle Scholar
Lopez, J. M. & Shen, J. 1998 An efficient spectral-projection method for the Navier–Stokes equations in cylindrical geometries: I. Axisymmetric cases. J. Comput. Phys. 139, 308–326.CrossRefGoogle Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2001 Instability and equilibration of centrifugally stable stratified Taylor–Couette flow. Phys. Rev. Lett. 86, 5270–5273.Google Scholar
Ostilla-Mónico, R., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Turbulence decay towards the linearly stable regime of Taylor–Couette flow. J. Fluid Mech. 748, R3.CrossRefGoogle Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.Google Scholar
Rayleigh, L. 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Richard, D. & Zahn, J.-P. 1999 Turbulence in differentially rotating flows. Astron. Astrophys. 347, 734–738.Google Scholar
Rüdiger, G. & Shalybkov, D. A. 2009 Stratorotational instability in MHD Taylor–Couette flows. Astron. Astrophys. 493, 375–383.Google Scholar
Shalybkov, D. & Rüdiger, G. 2005 Stability of density-stratified viscous Taylor–Couette flows. Astron. Astrophys. 438 (2), 411–417.Google Scholar
Turner, N. J., Fromang, S., Gammie, C., Klahr, H., Lesur, G., Wardle, M. & Bai, X.-N. 2014 Transport and Accretion in Planet-Forming Disks. University of Arizona Press.Google Scholar
Velikhov, E. P. 1959 Stability of an ideally conducting liquid flowing between cylinders rotating in a magnetic field. J. Expl Theor. Phys. 36, 1398–1404.Google Scholar
Yavneh, I., McWilliams, J. C. & Molemaker, M. J. 2001 Non-axisymmetric instability of centrifugally stable stratified Taylor–Couette flow. J. Fluid Mech. 448, 1–21.Google Scholar
Zeldovich, Y. B. 1981 On the friction of fluids between rotating cylinders. Proc. R. Soc. Lond. A 374, 299–312.Google Scholar