Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cao, Shibin
Hao, Jiaao
Klioutchnikov, Igor
Olivier, Herbert
Heufer, Karl Alexander
and
Wen, Chih-Yung
2021.
Leading-edge bluntness effects on hypersonic three-dimensional flows over a compression ramp.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Hao, Jiaao
Cao, Shibin
Wen, Chih-Yung
and
Olivier, Herbert
2021.
Occurrence of global instability in hypersonic compression corner flow.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Li, Fei
Choudhari, Meelan M.
Paredes, Pedro
and
Scholten, Anton
2022.
Nonlinear Evolution of Instabilities in a Laminar Separation Bubble at Hypersonic Mach Number.
Chiapparino, Giuseppe
and
Stemmer, Christian
2022.
Numerical investigation of a Mach 6 hypersonic laminar flow on two-dimensional cold-wall compression corners with controlled surface roughness.
International Journal of Heat and Fluid Flow,
Vol. 94,
Issue. ,
p.
108937.
Cao, Shibin
Hao, Jiaao
Klioutchnikov, Igor
Wen, Chih-Yung
Olivier, Herbert
and
Heufer, Karl Alexander
2022.
Transition to turbulence in hypersonic flow over a compression ramp due to intrinsic instability.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Sawant, Saurabh S.
Theofilis, V.
and
Levin, D.A.
2022.
On the synchronisation of three-dimensional shock layer and laminar separation bubble instabilities in hypersonic flow over a double wedge.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Lugrin, Mathieu
Nicolas, François
Severac, Nicolas
Tobeli, Jean-Pierre
Beneddine, Samir
Garnier, Eric
Esquieu, Sebastien
and
Bur, Reynald
2022.
Transitional shockwave/boundary layer interaction experiments in the R2Ch blowdown wind tunnel.
Experiments in Fluids,
Vol. 63,
Issue. 2,
Lugrin, Mathieu
Beneddine, Samir
Garnier, Eric
and
Bur, Reynald
2022.
Multi-scale study of the transitional shock-wave boundary layer interaction in hypersonic flow.
Theoretical and Computational Fluid Dynamics,
Vol. 36,
Issue. 2,
p.
277.
Hao, Jiaao
Fan, Jianhui
Cao, Shibin
and
Wen, Chih-Yung
2022.
Three-dimensionality of hypersonic laminar flow over a double cone.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Hong, Qizhen
Hao, Jiaao
Uy, Ken Chun Kit
Wen, Chih-Yung
and
Sun, Quanhua
2022.
Thermochemical nonequilibrium effects on high-enthalpy double-wedge flows.
Physics of Fluids,
Vol. 34,
Issue. 6,
Sadagopan, Aravinth
Huang, Daning
Jirasek, Adam
Seidel, Jürgen
Pandey, Anshuman
and
Casper, Katya M.
2022.
An Experimental and Computational Correlation Study for Fluid-Thermal-Structural Interaction of a Control Surface in Hypersonic Flow.
Chen, Zongnan
Hao, Jiaao
and
Wen, Chih-Yung
2022.
Control of supersonic compression corner flow using a plasma actuator.
Physics of Fluids,
Vol. 34,
Issue. 7,
Fan, Jianhui
Hao, Jiaao
and
Wen, Chih-Yung
2022.
Nonlinear interactions of global instabilities in hypersonic laminar flow over a double cone.
Physics of Fluids,
Vol. 34,
Issue. 12,
Dwivedi, Anubhav
Sidharth, G.S.
and
Jovanović, Mihailo R.
2022.
Oblique transition in hypersonic double-wedge flow.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Cao, Shibin
Hao, Jiaao
Guo, Peixu
Wen, Chih-Yung
and
Klioutchnikov, Igor
2023.
Stability of hypersonic flow over a curved compression ramp.
Journal of Fluid Mechanics,
Vol. 957,
Issue. ,
Davami, Jonathan
Juliano, Thomas J.
Scholten, Anton
and
Paredes, Pedro
2023.
Hypersonic Shock-Wave/Boundary-Layer Interactions on the ROTEX-T Cone/Flare.
Holman, Jiří
2023.
Numerical Solution of Transition to Turbulence over Compressible Ramp at Hypersonic Velocity.
Mathematics,
Vol. 11,
Issue. 17,
p.
3684.
Chiapparino, Giuseppe
and
Stemmer, Christian
2023.
Numerical investigation of a Mach 6 laminar shock-wave/boundary-layer interaction on a two-dimensional ramp with 3D controlled surface roughness.
International Journal of Heat and Fluid Flow,
Vol. 103,
Issue. ,
p.
109193.
Sadagopan, Aravinth
Huang, Daning
Jirasek, Adam
Seidel, Jürgen
Pandey, Anshuman
and
Casper, Katya M.
2023.
Hypersonic Fluid–Thermal–Structural Interaction of Cone–Slice–Ramp: Computations with Experimental Validation.
AIAA Journal,
Vol. 61,
Issue. 11,
p.
4752.
Ninni, Davide
Bonelli, Francesco
and
Pascazio, Giuseppe
2023.
Simulation of High-Enthalpy Turbulent Shock Wave/Boundary Layer Interaction Using a RANS Approach.
Aerotecnica Missili & Spazio,
Vol. 102,
Issue. 4,
p.
323.
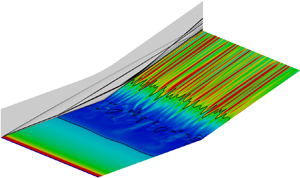
 $4.2\times 10^{5}$ based on the flat plate length. The DNS results are validated by comparison with experimental data and theoretical predictions. It is shown that even in the absence of external disturbances, streamwise heat flux streaks form on the ramp surface downstream of reattachment, and that they are non-uniformly distributed in the spanwise direction. The surface heat flux exhibits a low-frequency unsteadiness, which propagates in the streamwise direction. Additionally, the unsteadiness of the heat flux streaks downstream of reattachment is coupled with a pulsation of the reattachment position. By conducting a dynamic mode decomposition (DMD) analysis, several oscillatory modes, characterised by streamwise low-frequency periodicity, are revealed in the separation bubble flow. The DNS results are further explained by a global stability analysis (GSA). Particularly, the flow structure of the leading DMD modes is consistent with that of the oscillatory unstable modes identified by the GSA. It is therefore concluded that the global instabilities are responsible for the unsteadiness of the considered compression ramp flow.
$4.2\times 10^{5}$ based on the flat plate length. The DNS results are validated by comparison with experimental data and theoretical predictions. It is shown that even in the absence of external disturbances, streamwise heat flux streaks form on the ramp surface downstream of reattachment, and that they are non-uniformly distributed in the spanwise direction. The surface heat flux exhibits a low-frequency unsteadiness, which propagates in the streamwise direction. Additionally, the unsteadiness of the heat flux streaks downstream of reattachment is coupled with a pulsation of the reattachment position. By conducting a dynamic mode decomposition (DMD) analysis, several oscillatory modes, characterised by streamwise low-frequency periodicity, are revealed in the separation bubble flow. The DNS results are further explained by a global stability analysis (GSA). Particularly, the flow structure of the leading DMD modes is consistent with that of the oscillatory unstable modes identified by the GSA. It is therefore concluded that the global instabilities are responsible for the unsteadiness of the considered compression ramp flow.


