Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T10:27:23.172Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient growth in the near wake region of the flow past a finite span wing

Published online by Cambridge University Press:  13 March 2019

Navrose Open the ORCID record for Navrose [Opens in a new window] ,
V. Brion  and
L. Jacquin
Navrose
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur 208 016, India
V. Brion
Affiliation:
Département d’Aérodynamique Aéroélasticité Aéroacoustique (DAAA), ONERA, 92190 Meudon, France
L. Jacquin
Affiliation:
Département d’Aérodynamique Aéroélasticité Aéroacoustique (DAAA), ONERA, 92190 Meudon, France
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate optimal perturbation in the flow past a finite aspect ratio (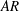$AR$) wing. The optimization is carried out in the regime where the fully developed flow is steady. Parametric study over time horizon (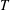$T$), Reynolds number (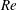$Re$), 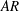$AR$, angle of attack and geometry of the wing cross-section (flat plate and NACA0012 airfoil) shows that the general shape of linear optimal perturbation remains the same over the explored parameter space. Optimal perturbation is located near the surface of the wing in the form of chord-wise periodic structures whose strength decreases from the root towards the tip. Direct time integration of the disturbance equations, with and without nonlinear terms, is carried out with linear optimal perturbation as initial condition. In both cases, the optimal perturbation evolves as a downstream travelling wavepacket whose speed is nearly the same as that of the free stream. The energy of the wavepacket increases in the near wake region, and is found to remain nearly constant beyond the vortex roll-up distance in nonlinear simulations. The nonlinear wavepacket results in displacement of the tip vortex. In this situation, the motion of the tip vortex resembles that observed during vortex meandering/wandering in wind tunnel experiments. Results from computation carried out at higher 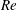$Re$ suggest that, even beyond the steady flow regime, a perturbation wavepacket originating near the wing might cause meandering of tip vortices.

JFM classification

Flow Control: Flow Control Vortex Flows: Vortex Flows Wakes/Jets: Wakes/Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 399 - 430
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Ehrenstein, U., Gallaire, F. & Henningson, D. S. 2008 Global two-dimensional stability measures of the flat plate boundary-layer flow. Eur. J. Mech. (B/Fluids) 27, 501–513.Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16 (1), L1–L4.Google Scholar
Antkowiak, A. & Brancher, P. 2007 On vortex rings around vortices: an optimal mechanism. J. Fluid Mech. 578, 295–304.Google Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.Google Scholar
Bilanin, A. & Widnall, S.1973 Aircraft wake dissipation by sinusoidal instability and vortex breakdown. AIAA Paper 73-107.Google Scholar
Brion, V., Sipp, D. & Jacquin, L. 2007 Optimal amplification of the Crow instability. Phys. Fluids 19 (11), 111703.Google Scholar
Cherubini, S. & De Palma, P. 2013 Nonlinear optimal perturbations in a Couette flow: bursting and transition. J. Fluid Mech. 716, 251–279.Google Scholar
Cherubini, S., De Palma, P., Robinet, J.-C. & Bottaro, A. 2011 The minimal seed of turbulent transition in the boundary layer. J. Fluid Mech. 689, 221–253.Google Scholar
Corbett, P. & Bottaro, A. 2000 Optimal perturbations for boundary layers subject to streamwise pressure gradient. Phys. Fluids 12, 120–130.Google Scholar
Cotel, A. J. & Breidenthal, R. E. 1999 Turbulence inside a vortex. Phys. Fluids 11, 3026–3029.Google Scholar
Crouch, J. D. 1997 Instability and transient growth for two trailing-vortex pairs. J. Fluid Mech. 350, 311–330.Google Scholar
Crouch, J. D., Miller, G. D. & Spalart, P. R. 2001 Active-control system for breakup of airplane trailing vortices. AIAA J. 39 (12), 2374–2381.Google Scholar
Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.Google Scholar
Crow, S. C. & Bate, E. R. 1976 Lifespan of trailing vortices in a turbulent atmosphere. J. Aircraft 13 (7), 476–482.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large-scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
Czech, M., Miller, G., Crouch, J. & Strelets, M.2004 Near-field evolution of trailing vortices behind aircraft with flaps deployed. AIAA Paper 2004-2149.Google Scholar
Dacles-Mariani, J., Zilliac, G. G., Chow, J. S. & Bradshaw, P. 1995 Numerical/experimental study of a wingtip vortex in the near field. AIAA J. 33, 1561–1568.Google Scholar
Donnadieu, C., Ortiz, S., Chomaz, J.-M. & Billant, P. 2009 Three-dimensional instabilities and transient growth of a counter-rotating vortex pair. Phys. Fluids 21 (9), 094102.Google Scholar
Edstrand, A. M., Davis, T. B., Schmid, P. J., Taira, K. & Cattafesta, L. N. 2016 On the mechanism of trailing vortex wandering. J. Fluid Mech. 801, R1.Google Scholar
Edstrand, A. M., Schmid, P. J., Taira, K. & Cattafesta, L. N. 2018 A parallel stability analysis of a trailing vortex wake. J. Fluid Mech. 837, 858–895.Google Scholar
Fabre, D. & Jacquin, L. 2000 Stability of a four-vortex aircraft wake model. Phys. Fluids 12 (10), 2438–2443.Google Scholar
Fabre, D., Jacquin, L. & Loof, A. 2002 Optimal perturbations in a four-vortex aircraft wake in counter-rotating configuration. J. Fluid Mech. 451, 319–328.Google Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
Farrell, B. F. 1988 Optimal excitation of perturbations in viscous shear flow. Phys. Fluids 31 (8), 2093.Google Scholar
Fischer, P., Lottes, J. & Kerkemeier, S.2008 Nek5000 Web Page. http://nek5000.mcs.anl.gov.Google Scholar
Fontane, J., Fabre, D. & Brancher, P. 2008 Stochastic forcing of the Lamb–Oseen vortex. J. Fluid Mech. 613, 233–254.Google Scholar
Jacquin, L., Fabre, D., Geffroy, P. & Coustols, E.2001 The properties of a transport aircraft wake in the extended near field – an experimental study. AIAA Paper 2001-1038.Google Scholar
Johnson, H., Brion, V. & Jacquin, L. 2016 Crow instability: nonlinear response to the linear optimal perturbation. J. Fluid Mech. 795, 652–670.Google Scholar
Jugier, R.2016 Stabilité bidimensionnelle de modeles de sillage d’aéronefs. PhD thesis.Google Scholar
Kerswell, R. R. 2018 Nonlinear nonmodal stability theory. Annu. Rev. Fluid Mech. 50 (1), 319–345.Google Scholar
Krasny, R. 1987 Computation of vortex sheet roll-up in the Trefftz plane. J. Fluid Mech. 184, 123–155.Google Scholar
Leweke, T., Le Dizés, S. & Williamson, C. H. K. 2016 Dynamics and instabilities of vortex pair. Annu. Rev. Fluid Mech. 48, 507–541.Google Scholar
Moore, D. W. & Saffman, P. G. 1973 Axial flow in laminar trailing vortices. Proc. R. Soc. Lond. A 333, 491–508.Google Scholar
Navrose, J. H., Brion, V., Jacquin, L. & Robinet, J. C. 2018 Optimal perturbation for 2D vortex systems: route to non-axisymmetric state. J. Fluid Mech. 855, 922–952.Google Scholar
Orr, W. McF. 1907 Stability or instability of the steady motions of a perfect liquid. Proc. Ir. Acad. Sect. A, Math. Astron. Phys. Sci. 27, 9–69.Google Scholar
Ortega, J. M. & Savaş, O. 2001 Rapidly growing instability mode in trailing multiple-vortex wakes. AIAA J. 39 (4), 750–754.Google Scholar
Pradeep, D. S. & Hussain, F. 2006 Transient growth of perturbations in a vortex column. J. Fluid Mech. 550, 251–288.Google Scholar
Rennich, S. C. & Lele, S. K. 1999 Method for accelerating the destruction of aircraft wake vortices. J. Aircraft 36 (2), 398–404.Google Scholar
Roy, C. & Leweke, T.2008 Experiments on vortex meandering. European project ‘FAR-Wake’ (AST4-CT-2005-012238), Tech. Rep. TR 1.1.1-4.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Schmid, P. J. & Brandt, L. 2014 Analysis of fluid systems: stability, receptivity, sensitivity lecture notes from the FLOW-NORDITA summer school on advanced instability methods for complex flows, Stockholm, Sweden, 2013. Appl. Mech. Rev. 66 (2), 024803.Google Scholar
Shur, M. L., Strelets, M. K., Travin, A. K. & Spalart, P. R. 2000 Turbulence modeling in rotating and curved channels: assessing the Spalart–Shur correction. AIAA J. 38, 784–792.Google Scholar
Schrader, L.-U., Brandt, L. & Henningson, D. S. 2009 Receptivity mechanisms in three-dimensional boundary-layer flows. J. Fluid Mech. 618, 209–241.Google Scholar
Spalart, P. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30 (1), 107–138.Google Scholar
Trefethen, L., Trefethen, A., Reddy, S. & Driscoll, T. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.Google Scholar
Zeman, O. 1995 The persistence of trailing vortices: a modeling study. Phys. Fluids 7 (1), 135–143.Google Scholar
Zuccher, S., Bottaro, A. & Luchini, P. 2006 Algebraic growth in a Blasius boundary layer: nonlinear optimal disturbances. Eur. J. Mech. (B/Fluids) 25, 1–17.Google Scholar