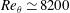1 Introduction
Turbulent boundary layers account for up to 50 % of the drag and therefore fuel consumption of modern aircraft (Schrauf Reference Schrauf2005). Turbulent flows also lead to enhanced exchange processes, such as mixing and heat transfer, present, for instance, in large-scale meteorological phenomena. Such characteristics have consequently led to efforts concerning a better understanding of the dynamics of these flows, both in terms of predictive models and their use to control the fluctuations on the near-wall region, where the highest values of shear and turbulent production are present (Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010).
Given their practical importance, several studies have aimed over the last decades at achieving a deeper understanding of the turbulent structures in the near-wall region of wall-bounded flows. The current understanding of the flow behaviour in this region involves a self-sustained turbulence regeneration cycle (Waleffe Reference Waleffe1995, Reference Waleffe1997; Jiménez & Pinelli Reference Jiménez and Pinelli1999; Panton Reference Panton2001; Moehlis, Faisst & Eckhardt Reference Moehlis, Faisst and Eckhardt2004). Coherent turbulent structures comprise a hierarchical ordering along the wall-normal direction (Flores & Jiménez Reference Flores and Jiménez2010; Jiménez Reference Jiménez2012, Reference Jiménez2013) and exhibit long life times in the streamwise direction, as can be recognized from works of Favre, Gaviglio & Dumas (Reference Favre, Gaviglio and Dumas1967), Blackwelder & Kovasznay (Reference Blackwelder and Kovasznay1972), Wark & Nagib (Reference Wark and Nagib1991), Kim & Adrian (Reference Kim and Adrian1999) and Hutchins & Marusic (Reference Hutchins and Marusic2007). Moreover, large-scale turbulent structures make a significant contribution to the turbulent kinetic energy and Reynolds stresses in the outer layer (Komminaho, Lundbladh & Johansson Reference Komminaho, Lundbladh and Johansson1996; Guala, Hommema & Adrian Reference Guala, Hommema and Adrian2006) and have been recently shown to imprint their presence in the near-wall region (Hoyas & Jiménez Reference Hoyas and Jiménez2006), an effect modelled via an amplitude modulation (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009; Marusic et al. Reference Marusic, Mathis and Hutchins2010; Schlatter & Örlü Reference Schlatter and Örlü2010; Bernardini & Pirozzoli Reference Bernardini and Pirozzoli2011; Vinuesa et al. Reference Vinuesa, Hites, Wark and Nagib2015; Dogan et al. Reference Dogan, Örlü, Gatti, Vinuesa and Schlatter2019).
Approaches based on the linearization of the Navier–Stokes operator have been recently shown to enable the extraction of some of the features of these large-scale structures; in such methods the equations are linearized around the mean turbulent flow (as opposed to the linearization around a laminar base flow, as is the case for transitional problems). This could be considered analogously to the laminar base flow (Crighton & Gaster Reference Crighton and Gaster1976) of the most usual analysis of transitional cases. Of particular importance was the realization that even stable flows may exhibit strong transient amplifications, which are related to the non-normality of the Navier–Stokes operator (Trefethen et al. Reference Trefethen, Trefethen, Reddy and Driscoll1993; Farrell & Ioannou Reference Farrell and Ioannou1996; Schmid & Henningson Reference Schmid and Henningson2012). The transient growth analysis has also been used to study turbulent flows, as in the studies by del Álamo & Jiménez (Reference del Álamo and Jiménez2006) and Pujals et al. (Reference Pujals, García-Villalba, Cossu and Depardon2009) in channels and Cossu, Pujals & Depardon (Reference Cossu, Pujals and Depardon2009) in boundary layers, all of which deal with a linearization of the equations around the turbulent mean profile.
In related works, but using a different strategy, these large-scale structures have been studied by means of a resolvent-based method (Hwang & Cossu Reference Hwang and Cossu2010; McKeon & Sharma Reference McKeon and Sharma2010; McKeon, Sharma & Jacobi Reference McKeon, Sharma and Jacobi2013; McKeon Reference McKeon2017). The basic idea consists of performing a Reynolds decomposition and replacing the nonlinear fluctuation terms of the Navier–Stokes equations by a forcing to the linear operator. Doing so, the nonlinear forcing is treated as an unknown, and the most amplified flow responses to such forcings are sought. The resolvent operator is then used to extract information from the flow and it has been shown to reproduce relevant features, such as the spectral proper orthogonal decomposition (SPOD) modes of the streamwise velocity fluctuations of a turbulent boundary layer over and airfoil and in a turbulent free jet (Abreu, Cavalieri & Wolf Reference Abreu, Cavalieri and Wolf2017; Towne, Schmidt & Colonius Reference Towne, Schmidt and Colonius2018).
The works cited above focus on frequency-domain characteristics of the flow. The model of Marusic and co-workers (Mathis et al. Reference Mathis, Hutchins and Marusic2009; Marusic et al. Reference Marusic, Mathis and Hutchins2010; Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2011) treats the interaction among different wall-normal directions as an amplitude modulation, and is able to predict with compelling agreement the statistics of the fluctuations in the near-wall region from measurements in the logarithmic layer. This model is, however, unable to accurately capture the instantaneous flow field, one of the necessary ingredients for flow control applications. Examples of models which are able to do such time-domain, instantaneous predictions may be found in the recent works of Baars, Hutchins & Marusic (Reference Baars, Hutchins and Marusic2016) and Illingworth, Monty & Marusic (Reference Illingworth, Monty and Marusic2018), which make use of spectral stochastic estimation and linear estimation via a state observer, respectively, to obtain time-domain predictions for the large-scale structures in a turbulent boundary layer.
In this work we propose to follow a somewhat different strategy based on the cross-spectral density between various wall-normal separated positions. This approach allows us to obtain linear and nonlinear frequency response functions which, when inversed Fourier transformed, lead to convolution kernels; these will be referred to as transfer functions (TFs). This method has already been used by this group to model a high-Reynolds-number turbulent jet (Sasaki et al. Reference Sasaki, Piantanida, Cavalieri and Jordan2017) and as a reduced-order model for control of transitional flows (Sasaki et al. Reference Sasaki, Morra, Fabbiane, Cavalieri, Hanifi and Henningson2018a ,Reference Sasaki, Tissot, Cavalieri, Silvestre, Jordan and Biau b ). All these previous studies have led to very satisfactory results.
Since the proposed method, when applied to a boundary layer, relies uniquely on the temporal and spanwise data, it allows a considerable flexibility in terms of the definition of inputs and outputs, both in terms of wall-normal positions and quantities to be estimated. One interesting feature that is explored in this study is the use of measurements at the wall to estimate the flow at higher wall-normal locations, which could have direct implications for experimental implementations. ‘Off-design’ evaluations, where the models are constructed and tested at different Reynolds numbers, are also explored here. The possibility to apply the methods at much higher Reynolds numbers, reducing the number of measurements to be conducted, is expected to have a significant appeal to experimental and practical applications.
Finally, the formalism written in terms of transfer functions permits to extract the relationship that exists between the different inputs and outputs of the system, allowing to obtain the footprint of the large-scale outer-region wall structures on the near-wall region.
The database under study is the highly resolved and well-validated large-eddy simulation (LES) zero-pressure-gradient (ZPG) turbulent boundary layer (TBL) by Eitel-Amor, Örlü & Schlatter (Reference Eitel-Amor, Örlü and Schlatter2014), where the highest available Reynolds number based on the momentum thickness is
![]() $Re_{\unicode[STIX]{x1D703}}=8300$
.
$Re_{\unicode[STIX]{x1D703}}=8300$
.
This article is organized as follows: in § 2 the LES database is presented, § 3 presents the calculated coherence for different wall-normal positions and justifies the application of linear methods to this flow. The linear and nonlinear transfer functions under consideration are presented in § 4 whereas the results and analysis are discussed in § 5, along with a comparison of the different methods. The off-design and robustness analysis are performed in § 6 and a comparison with other methods available in the literature is given in § 7. The conclusions of the study are presented in § 8. Finally, the appendices present details of the frequency-domain tools used in this work, namely the ensemble averaging for the calculation of spectra and the spectral conditioning for the decorrelation of inputs.
2 Description of the numerical database
The set-up of the LES by Eitel-Amor et al. (Reference Eitel-Amor, Örlü and Schlatter2014) corresponds to a flat plate where a statistically two-dimensional ZPG TBL, with density
![]() $\unicode[STIX]{x1D70C}$
, viscosity
$\unicode[STIX]{x1D70C}$
, viscosity
![]() $\unicode[STIX]{x1D708}$
and free-stream velocity
$\unicode[STIX]{x1D708}$
and free-stream velocity
![]() $U_{\infty }$
develops along the streamwise direction. The dimensions of the domain are
$U_{\infty }$
develops along the streamwise direction. The dimensions of the domain are
![]() $L_{x}\times L_{y}\times L_{z}=13\,500\times 400\times 540$
in the streamwise, wall-normal and spanwise directions, where non-dimensionalization with the displacement thickness at the inlet
$L_{x}\times L_{y}\times L_{z}=13\,500\times 400\times 540$
in the streamwise, wall-normal and spanwise directions, where non-dimensionalization with the displacement thickness at the inlet
![]() $\unicode[STIX]{x1D6FF}_{0}^{\ast }$
is considered. Here we employ a Reynolds decomposition of the velocity field into a spanwise and temporal average
$\unicode[STIX]{x1D6FF}_{0}^{\ast }$
is considered. Here we employ a Reynolds decomposition of the velocity field into a spanwise and temporal average
![]() $U(x,y)$
and the fluctuating velocities,
$U(x,y)$
and the fluctuating velocities,
![]() $u(x,y,z,t)$
,
$u(x,y,z,t)$
,
![]() $v(x,y,z,t)$
and
$v(x,y,z,t)$
and
![]() $w(x,y,z,t)$
. The outer velocity scale is
$w(x,y,z,t)$
. The outer velocity scale is
![]() $U_{\infty }$
, and the outer length scale is
$U_{\infty }$
, and the outer length scale is
![]() $\unicode[STIX]{x1D6FF}_{99}$
, i.e. the wall-normal position where the mean velocity
$\unicode[STIX]{x1D6FF}_{99}$
, i.e. the wall-normal position where the mean velocity
![]() $U(x,y)$
reaches 99 % of
$U(x,y)$
reaches 99 % of
![]() $U_{\infty }$
. The Reynolds number
$U_{\infty }$
. The Reynolds number
![]() $Re_{\unicode[STIX]{x1D703}}=U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708}$
is then defined in terms of the momentum thickness
$Re_{\unicode[STIX]{x1D703}}=U_{\infty }\unicode[STIX]{x1D703}/\unicode[STIX]{x1D708}$
is then defined in terms of the momentum thickness
![]() $\unicode[STIX]{x1D703}$
. The inner scale is based on the friction velocity
$\unicode[STIX]{x1D703}$
. The inner scale is based on the friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}=\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}}$
, which is obtained from the mean shear stress at the wall,
$u_{\unicode[STIX]{x1D70F}}=\sqrt{\unicode[STIX]{x1D70F}_{w}/\unicode[STIX]{x1D70C}}$
, which is obtained from the mean shear stress at the wall,
![]() $\unicode[STIX]{x1D70F}_{w}$
and the inner length scale is the viscous length
$\unicode[STIX]{x1D70F}_{w}$
and the inner length scale is the viscous length
![]() $l_{\ast }=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
. Inner scaling will be denoted by the superscript
$l_{\ast }=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
. Inner scaling will be denoted by the superscript
![]() $+$
. The friction Reynolds number is then defined as
$+$
. The friction Reynolds number is then defined as
![]() $Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D708}$
.
$Re_{\unicode[STIX]{x1D70F}}=u_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}_{99}/\unicode[STIX]{x1D708}$
.
Following a procedure similar to that in wind-tunnel experiments, laminar flow enters the domain and is then forced to transition via a tripping (see Schlatter & Örlü (Reference Schlatter and Örlü2012) for a complete description of the method). The flow is tripped close to the leading edge, at
![]() $Re_{\unicode[STIX]{x1D703}}=180$
, where the tripping is more efficient. Transition to turbulence is considered to be complete at
$Re_{\unicode[STIX]{x1D703}}=180$
, where the tripping is more efficient. Transition to turbulence is considered to be complete at
![]() $Re_{\unicode[STIX]{x1D703}}\geqslant 600$
, as shown in Eitel-Amor et al. (Reference Eitel-Amor, Örlü and Schlatter2014). The highest Reynolds number to be considered in this work is of
$Re_{\unicode[STIX]{x1D703}}\geqslant 600$
, as shown in Eitel-Amor et al. (Reference Eitel-Amor, Örlü and Schlatter2014). The highest Reynolds number to be considered in this work is of
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
, located upstream of the end of the computational domain in order to avoid outflow effects.
$Re_{\unicode[STIX]{x1D703}}=8200$
, located upstream of the end of the computational domain in order to avoid outflow effects.
This study will focus on the data at the streamwise position corresponding to
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
(
$Re_{\unicode[STIX]{x1D703}}=4430$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=1324$
), however the cases corresponding to
$Re_{\unicode[STIX]{x1D70F}}=1324$
), however the cases corresponding to
![]() $Re_{\unicode[STIX]{x1D703}}=2240$
(
$Re_{\unicode[STIX]{x1D703}}=2240$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=704$
) and
$Re_{\unicode[STIX]{x1D70F}}=704$
) and
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
(
$Re_{\unicode[STIX]{x1D703}}=8200$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=2370$
) will also be analysed in order to evaluate the effect of the Reynolds number in the predictions and to perform the off-design studies.
$Re_{\unicode[STIX]{x1D70F}}=2370$
) will also be analysed in order to evaluate the effect of the Reynolds number in the predictions and to perform the off-design studies.
The number of collocation points employed in the simulation is
![]() $13\,824\times 513\times 1152$
in the streamwise, wall-normal and spanwise directions. As shown by Eitel-Amor et al. (Reference Eitel-Amor, Örlü and Schlatter2014) this resolution corresponds to a very finely resolved LES, in excellent agreement with DNS studies of ZPG TBL. The spectral code SIMSON (Chevalier, Lundbladh & Henningson Reference Chevalier, Lundbladh and Henningson2007) is used for this simulation, and was previously used in a number of studies by this group (Schlatter et al.
Reference Schlatter, Örlü, Li, Brethouwer, Fransson, Johansson, Alfredsson and Henningson2009; Schlatter & Örlü Reference Schlatter and Örlü2010).
$13\,824\times 513\times 1152$
in the streamwise, wall-normal and spanwise directions. As shown by Eitel-Amor et al. (Reference Eitel-Amor, Örlü and Schlatter2014) this resolution corresponds to a very finely resolved LES, in excellent agreement with DNS studies of ZPG TBL. The spectral code SIMSON (Chevalier, Lundbladh & Henningson Reference Chevalier, Lundbladh and Henningson2007) is used for this simulation, and was previously used in a number of studies by this group (Schlatter et al.
Reference Schlatter, Örlü, Li, Brethouwer, Fransson, Johansson, Alfredsson and Henningson2009; Schlatter & Örlü Reference Schlatter and Örlü2010).
A total of 19 410 time samples is used, with a spacing in time of
![]() $\unicode[STIX]{x0394}t^{+}=0.5$
, which is appropriate for convergence of the statistics and is also adequate to correctly resolve the near-wall (which corresponds to a period
$\unicode[STIX]{x0394}t^{+}=0.5$
, which is appropriate for convergence of the statistics and is also adequate to correctly resolve the near-wall (which corresponds to a period
![]() $\unicode[STIX]{x1D706}_{t}^{+}\approx 100$
) and outer (
$\unicode[STIX]{x1D706}_{t}^{+}\approx 100$
) and outer (
![]() $\unicode[STIX]{x1D706}_{t}\approx 10\unicode[STIX]{x1D6FF}_{99}$
) peaks. The first half of the time samples is used to design the modelling methodologies and the other half to test them. The spanwise discretization results in 768 points separated by
$\unicode[STIX]{x1D706}_{t}\approx 10\unicode[STIX]{x1D6FF}_{99}$
) peaks. The first half of the time samples is used to design the modelling methodologies and the other half to test them. The spanwise discretization results in 768 points separated by
![]() $\unicode[STIX]{x0394}z^{+}=12$
, which is appropriate to capture the near-wall (with a typical spanwise wavelength
$\unicode[STIX]{x0394}z^{+}=12$
, which is appropriate to capture the near-wall (with a typical spanwise wavelength
![]() $\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
) and outer (
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
) and outer (
![]() $\unicode[STIX]{x1D706}_{z}\approx \unicode[STIX]{x1D6FF}_{99}$
) structures. For further details concerning the convergence of statistics of this simulation the reader is referred to Eitel-Amor et al. (Reference Eitel-Amor, Örlü and Schlatter2014).
$\unicode[STIX]{x1D706}_{z}\approx \unicode[STIX]{x1D6FF}_{99}$
) structures. For further details concerning the convergence of statistics of this simulation the reader is referred to Eitel-Amor et al. (Reference Eitel-Amor, Örlü and Schlatter2014).
3 Pre-multiplied spectra and coherence
Prior to the construction of the transfer functions, an evaluation of the behaviour of the two-dimensional spectra and the coherence between sets of positions separated along the wall-normal direction was performed. The objective of such assessment was to evaluate the suitability of models for the prediction.
The focus will be on three locations in the wall-normal direction,
![]() $y^{+}=15$
, 50 and 100, which correspond to positions in the near-wall region, just outside the buffer layer and representative of the logarithmic region, respectively. This may be observed in figure 1 which shows the mean flow profile, scaled in inner units, for the four Reynolds numbers evaluated in this work. Regions I, II, III and IV represent the viscous sublayer, buffer and logarithmic layers and wake region, respectively. The linear and logarithmic profiles are shown to better highlight the behaviour of the mean velocity profile; the inner and outer regions (the latter shown for
$y^{+}=15$
, 50 and 100, which correspond to positions in the near-wall region, just outside the buffer layer and representative of the logarithmic region, respectively. This may be observed in figure 1 which shows the mean flow profile, scaled in inner units, for the four Reynolds numbers evaluated in this work. Regions I, II, III and IV represent the viscous sublayer, buffer and logarithmic layers and wake region, respectively. The linear and logarithmic profiles are shown to better highlight the behaviour of the mean velocity profile; the inner and outer regions (the latter shown for
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
) are also shown on the upper part of the plot.
$Re_{\unicode[STIX]{x1D703}}=8200$
) are also shown on the upper part of the plot.
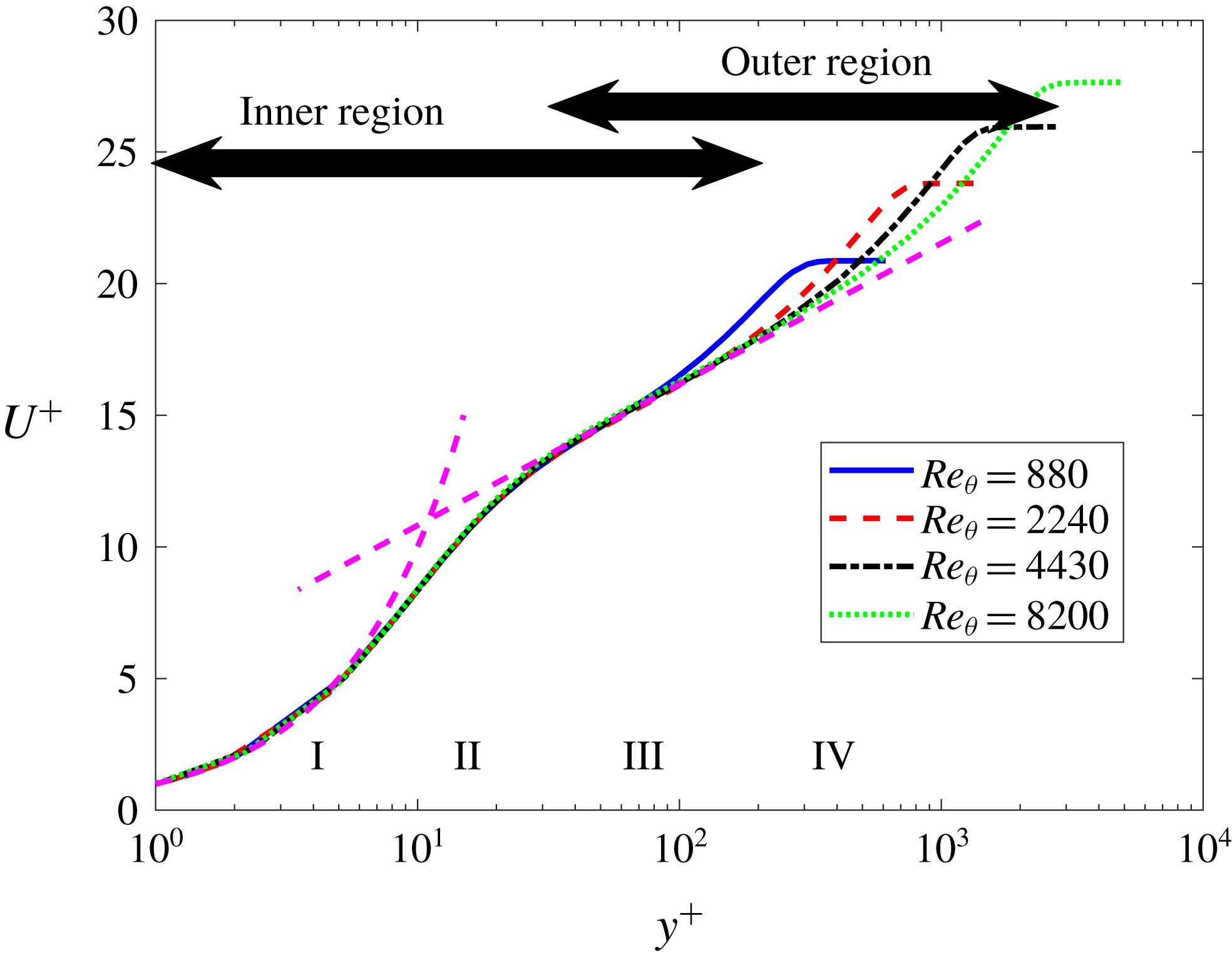
Figure 1. Inner-scaled mean velocity profiles for the four Reynolds numbers evaluated in the current study. Regions I, II, III and IV represent the viscous sublayer (
![]() $y^{+}\lessapprox 7$
), buffer (
$y^{+}\lessapprox 7$
), buffer (
![]() $7\lessapprox y^{+}\lessapprox 30$
) and logarithmic layers (
$7\lessapprox y^{+}\lessapprox 30$
) and logarithmic layers (
![]() $30\lessapprox y^{+}\lessapprox 220$
) and wake region (
$30\lessapprox y^{+}\lessapprox 220$
) and wake region (
![]() $220\lessapprox y^{+}$
until the edge of the boundary layer, for the
$220\lessapprox y^{+}$
until the edge of the boundary layer, for the
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
case). The pink dashed lines correspond to the linear (
$Re_{\unicode[STIX]{x1D703}}=8200$
case). The pink dashed lines correspond to the linear (
![]() $U^{+}=y^{+}$
) and logarithmic profiles (
$U^{+}=y^{+}$
) and logarithmic profiles (
![]() $U^{+}=1/\unicode[STIX]{x1D705}log(y^{+})+B$
, where
$U^{+}=1/\unicode[STIX]{x1D705}log(y^{+})+B$
, where
![]() $\unicode[STIX]{x1D705}=0.41$
and
$\unicode[STIX]{x1D705}=0.41$
and
![]() $B=5.1$
), respectively. The upper limit of the outer region corresponds to the
$B=5.1$
), respectively. The upper limit of the outer region corresponds to the
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
case, extending until the edge of the boundary layer.
$Re_{\unicode[STIX]{x1D703}}=8200$
case, extending until the edge of the boundary layer.
The inner-scaled, two-dimensional, pre-multiplied spectrum is defined as
![]() $E_{uu}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FD}/u_{\unicode[STIX]{x1D70F}}^{2}$
, where
$E_{uu}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FD}/u_{\unicode[STIX]{x1D70F}}^{2}$
, where
![]() $E_{uu}=\langle \hat{\hat{u} }\hat{\hat{u} }^{\ast }\rangle$
, with the double hat representing the double Fourier transform of
$E_{uu}=\langle \hat{\hat{u} }\hat{\hat{u} }^{\ast }\rangle$
, with the double hat representing the double Fourier transform of
![]() $u$
in the spanwise direction and time, the brackets
$u$
in the spanwise direction and time, the brackets
![]() $\langle \rangle$
denote an ensemble averaging as defined in appendix A,
$\langle \rangle$
denote an ensemble averaging as defined in appendix A,
![]() $\ast$
defines the complex conjugate,
$\ast$
defines the complex conjugate,
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $\unicode[STIX]{x1D6FD}$
are the frequency and spanwise wavenumbers and
$\unicode[STIX]{x1D6FD}$
are the frequency and spanwise wavenumbers and
![]() $\unicode[STIX]{x1D706}_{t}^{+}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}$
,
$\unicode[STIX]{x1D706}_{t}^{+}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}$
,
![]() $\unicode[STIX]{x1D706}_{z}^{+}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}$
, given in inner units. Spectra have been averaged using Welch’s method, using segments with 256 snapshots with 75 % overlap and a time discretization
$\unicode[STIX]{x1D706}_{z}^{+}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FD}$
, given in inner units. Spectra have been averaged using Welch’s method, using segments with 256 snapshots with 75 % overlap and a time discretization
![]() $\unicode[STIX]{x0394}t^{+}=0.5$
, with a triangular window leading to a frequency resolution of
$\unicode[STIX]{x0394}t^{+}=0.5$
, with a triangular window leading to a frequency resolution of
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}=0.05$
. Figure 2 shows the time signal and pre-multiplied spectra of the streamwise velocity fluctuation at three locations,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}^{+}=0.05$
. Figure 2 shows the time signal and pre-multiplied spectra of the streamwise velocity fluctuation at three locations,
![]() $y^{+}=15$
, 50 and 100, for the
$y^{+}=15$
, 50 and 100, for the
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
, (corresponding to
$Re_{\unicode[STIX]{x1D703}}=4430$
, (corresponding to
![]() $Re_{\unicode[STIX]{x1D70F}}=1324$
), case. Velocity fluctuations are normalized using the friction velocity
$Re_{\unicode[STIX]{x1D70F}}=1324$
), case. Velocity fluctuations are normalized using the friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}$
in the results shown in figure 2, and also for all time series presented later in the paper.
$u_{\unicode[STIX]{x1D70F}}$
in the results shown in figure 2, and also for all time series presented later in the paper.
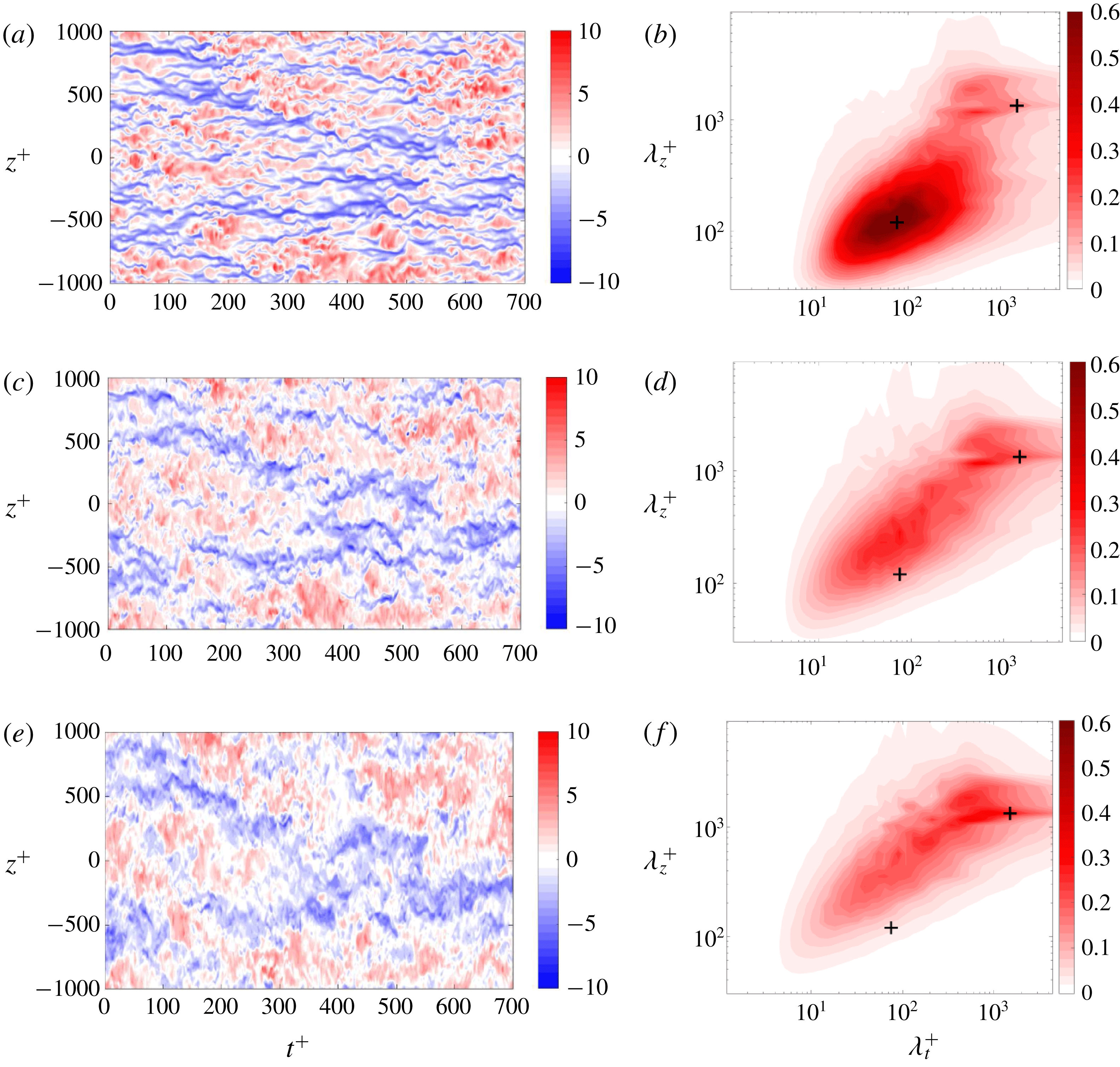
Figure 2. Behaviour of the streamwise velocity fluctuations and inner-scaled pre-multiplied two-dimensional spectra at different wall-normal positions for
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. The crosses correspond to reference locations for the inner (
$Re_{\unicode[STIX]{x1D703}}=4430$
. The crosses correspond to reference locations for the inner (
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
![]() $(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
$(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). The limits of the colour bar were kept the same between different plots to highlight the different amplitudes. (a) Instantaneous streamwise velocity fluctuations at
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). The limits of the colour bar were kept the same between different plots to highlight the different amplitudes. (a) Instantaneous streamwise velocity fluctuations at
![]() $y^{+}=15$
. (b) Pre-multiplied spectra at
$y^{+}=15$
. (b) Pre-multiplied spectra at
![]() $y^{+}=15$
. (c) Instantaneous streamwise velocity fluctuations at
$y^{+}=15$
. (c) Instantaneous streamwise velocity fluctuations at
![]() $y^{+}=50$
. (d) Pre-multiplied spectra at
$y^{+}=50$
. (d) Pre-multiplied spectra at
![]() $y^{+}=50$
. (e) Instantaneous streamwise velocity fluctuations at
$y^{+}=50$
. (e) Instantaneous streamwise velocity fluctuations at
![]() $y^{+}=100$
. (f) Pre-multiplied spectra at
$y^{+}=100$
. (f) Pre-multiplied spectra at
![]() $y^{+}=100$
.
$y^{+}=100$
.
The dominant spanwise wavelength of the fluctuations grows as one moves further in the wall-normal direction, which leads to a wider scale separation between the large-scale streaks in the outer region and the near-wall streaks, a feature which may be observed in the two-dimensional pre-multiplied spectra of figure 2. For
![]() $y^{+}=15$
, representative of the buffer layer, the classical near-wall streaks with spacing
$y^{+}=15$
, representative of the buffer layer, the classical near-wall streaks with spacing
![]() $\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
are observed, with a characteristic time
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
are observed, with a characteristic time
![]() $\unicode[STIX]{x1D706}_{t}^{+}\approx 100$
. In the outer region a secondary peak, which scales in outer units, is observed with characteristic scales
$\unicode[STIX]{x1D706}_{t}^{+}\approx 100$
. In the outer region a secondary peak, which scales in outer units, is observed with characteristic scales
![]() $\unicode[STIX]{x1D706}_{z}\approx \unicode[STIX]{x1D6FF}_{99}$
and
$\unicode[STIX]{x1D706}_{z}\approx \unicode[STIX]{x1D6FF}_{99}$
and
![]() $\unicode[STIX]{x1D706}_{t}\approx 10\unicode[STIX]{x1D6FF}_{99}/U_{\infty }$
. In order to extract the relation between near-wall and outer positions, the coherence between two sets of synchronized signals separated in the wall-normal direction was computed using time series of the streamwise velocity fluctuation. For a statistically two-dimensional ZPG TBL, which is homogeneous in the spanwise direction, we define:
$\unicode[STIX]{x1D706}_{t}\approx 10\unicode[STIX]{x1D6FF}_{99}/U_{\infty }$
. In order to extract the relation between near-wall and outer positions, the coherence between two sets of synchronized signals separated in the wall-normal direction was computed using time series of the streamwise velocity fluctuation. For a statistically two-dimensional ZPG TBL, which is homogeneous in the spanwise direction, we define:
where
![]() $y_{in}$
,
$y_{in}$
,
![]() $y_{out}$
correspond to the wall-normal position of the input/output pair of time series that are considered in the analysis. The coherence is a quantity analogous to the correlation, but defined in the frequency domain (here also in wavenumber domain, taking advantage of homogeneity of the spanwise coordinate) and it represents a metric of linear behaviour between two signals, for a given
$y_{out}$
correspond to the wall-normal position of the input/output pair of time series that are considered in the analysis. The coherence is a quantity analogous to the correlation, but defined in the frequency domain (here also in wavenumber domain, taking advantage of homogeneity of the spanwise coordinate) and it represents a metric of linear behaviour between two signals, for a given
![]() $(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
pair. Its value is normalized between zero and one, where the former indicates a complete random behaviour and the latter an exact linear relation between the two signals (namely an amplitude change and a phase shift). Linear, time and span invariant models with single input and single output lead to unit coherence between input and output (Bendat & Piersol Reference Bendat and Piersol2011); hence, coherence values close to one suggest the possibility of modelling the observed behaviour with a linear model.
$(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
pair. Its value is normalized between zero and one, where the former indicates a complete random behaviour and the latter an exact linear relation between the two signals (namely an amplitude change and a phase shift). Linear, time and span invariant models with single input and single output lead to unit coherence between input and output (Bendat & Piersol Reference Bendat and Piersol2011); hence, coherence values close to one suggest the possibility of modelling the observed behaviour with a linear model.
The objective that we will pursue in the next sections is to predict the behaviour of the fluctuations in the near-wall region, such that the output position will be fixed at
![]() $y^{+}=15$
, where a clear peak is observed in the pre-multiplied spectra shown in figure 2. Sample inputs are chosen at
$y^{+}=15$
, where a clear peak is observed in the pre-multiplied spectra shown in figure 2. Sample inputs are chosen at
![]() $y^{+}=50$
and
$y^{+}=50$
and
![]() $100$
, where the larger scales become prominent and in a third case using the wall-shear stress. The objective of the latter is to capture the finer-scale motions close to the wall.
$100$
, where the larger scales become prominent and in a third case using the wall-shear stress. The objective of the latter is to capture the finer-scale motions close to the wall.
Figure 3 shows the coherence for three pairs of positions. It is noticeable that for the higher wall-normal positions the long spanwise wavelengths are coherent. This observation is related to the wall footprint of large-scale motions that are attached to the wall, as in Marusic et al. (Reference Marusic, Mathis and Hutchins2010). We see that larger-scale structures at outer positions have a significant footprint at the buffer layer, with coherences ranging between 0.6 and 0.9 for wavelengths and periods corresponding to the outer peak. However, the near-wall peak
![]() $(\unicode[STIX]{x1D706}_{z}^{+},\unicode[STIX]{x1D706}_{t}^{+}=100,100)$
is seen to be incoherent with outer-layer disturbances. In turn, the coherence using wall-shear stress as input exhibits values close to unity at the lower wavelengths, corresponding to the near-wall peak in the pre-multiplied spectra of figure 2; this indicates that shear-stress fluctuations may be an interesting candidate as an input measurement for prediction of buffer-layer fluctuations (Örlü & Schlatter Reference Örlü and Schlatter2011).
$(\unicode[STIX]{x1D706}_{z}^{+},\unicode[STIX]{x1D706}_{t}^{+}=100,100)$
is seen to be incoherent with outer-layer disturbances. In turn, the coherence using wall-shear stress as input exhibits values close to unity at the lower wavelengths, corresponding to the near-wall peak in the pre-multiplied spectra of figure 2; this indicates that shear-stress fluctuations may be an interesting candidate as an input measurement for prediction of buffer-layer fluctuations (Örlü & Schlatter Reference Örlü and Schlatter2011).
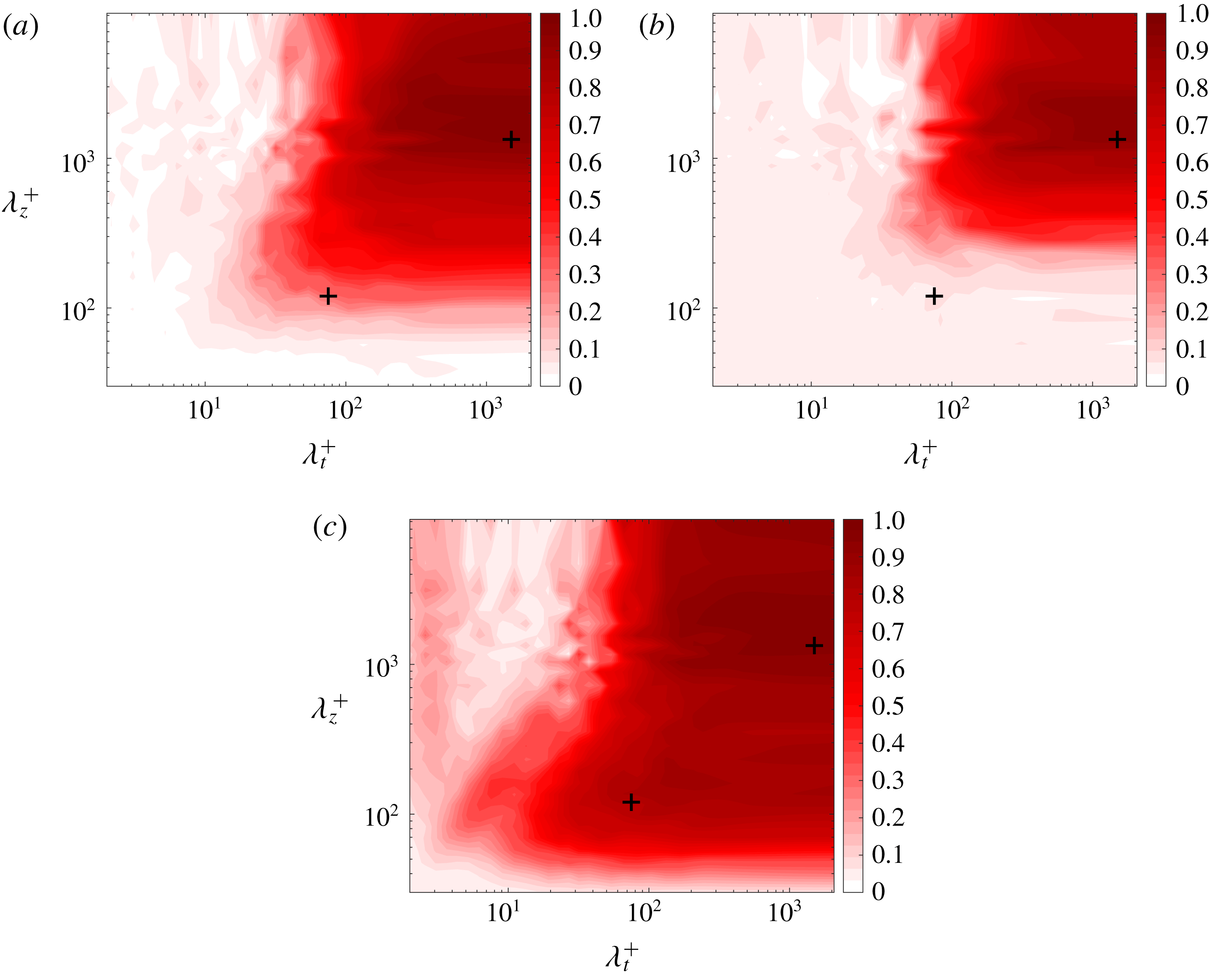
Figure 3. Coherence between two positions separated in the wall-normal direction, for
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. The crosses correspond to reference locations for the inner (
$Re_{\unicode[STIX]{x1D703}}=4430$
. The crosses correspond to reference locations for the inner (
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
![]() $(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
$(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). (a) Coherence between streamwise velocity fluctuations at
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). (a) Coherence between streamwise velocity fluctuations at
![]() $y^{+}=50$
and 15. (b) Coherence between streamwise velocity fluctuations
$y^{+}=50$
and 15. (b) Coherence between streamwise velocity fluctuations
![]() $y^{+}=100$
and 15. (c) Coherence between wall-shear stress and streamwise velocity fluctuations at
$y^{+}=100$
and 15. (c) Coherence between wall-shear stress and streamwise velocity fluctuations at
![]() $y^{+}=15$
.
$y^{+}=15$
.
In order to better assess the behaviour of the coherence and its relation to the peak in the two-dimensional spectra, figure 4 presents the one-dimensional pre-multiplied temporal spectrum (
![]() $E_{uu}^{1D}\unicode[STIX]{x1D714}/u_{\unicode[STIX]{x1D70F}}^{2}$
) as a function of the wall-normal direction overlaid on the one-dimensional coherence,
$E_{uu}^{1D}\unicode[STIX]{x1D714}/u_{\unicode[STIX]{x1D70F}}^{2}$
) as a function of the wall-normal direction overlaid on the one-dimensional coherence,
which is calculated between a pair of positions at the same spanwise location, one is at a fixed wall-normal location and the other one is moved. The reference input position is in the viscous sublayer, i.e. at
![]() $y_{in}^{+}=5$
and two Reynolds numbers were considered,
$y_{in}^{+}=5$
and two Reynolds numbers were considered,
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
(
$Re_{\unicode[STIX]{x1D703}}=4430$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=1324$
) and 8200 (
$Re_{\unicode[STIX]{x1D70F}}=1324$
) and 8200 (
![]() $Re_{\unicode[STIX]{x1D70F}}=2370$
). For both cases it is noticeable that the larger scales exhibit significant values of coherence with the near-wall region, illustrating the fact that the largest scales are indeed attached to the wall. It is also observed that, as the Reynolds number is increased, the larger scales remain coherent with the near-wall region until much further away from the wall, including the outer spectral peak. Wall-normal positions up to
$Re_{\unicode[STIX]{x1D70F}}=2370$
). For both cases it is noticeable that the larger scales exhibit significant values of coherence with the near-wall region, illustrating the fact that the largest scales are indeed attached to the wall. It is also observed that, as the Reynolds number is increased, the larger scales remain coherent with the near-wall region until much further away from the wall, including the outer spectral peak. Wall-normal positions up to
![]() $y^{+}\approx 500$
continue to exhibit coherence levels of 0.4 with the near wall indicating that the footprint of such large scales is clearly present for the
$y^{+}\approx 500$
continue to exhibit coherence levels of 0.4 with the near wall indicating that the footprint of such large scales is clearly present for the
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
case. This enables the use of data in the outer region to predict specific flow features close to the wall. As for the finer scales, they present high levels of coherence only close to the wall, which permits the use of local wall-shear-stress data or even universal signals to predict the inner-peak behaviour.
$Re_{\unicode[STIX]{x1D703}}=8200$
case. This enables the use of data in the outer region to predict specific flow features close to the wall. As for the finer scales, they present high levels of coherence only close to the wall, which permits the use of local wall-shear-stress data or even universal signals to predict the inner-peak behaviour.
The high values of coherence reported here motivate the use of predictive techniques for application in the turbulent zero-pressure-gradient boundary layer. Through this paper, such models will be defined in terms of linear and nonlinear transfer functions, which will be introduced in the next section.
Other studies using different methodologies, and based on experimental databases (Marusic et al.
Reference Marusic, Mathis and Hutchins2010; Baars et al.
Reference Baars, Hutchins and Marusic2016), perform analyses up to
![]() $Re_{\unicode[STIX]{x1D70F}}=19\,000$
and observe that the footprint of the larger scales on the near-wall region remains. Particularly, the work of Baars et al. (Reference Baars, Hutchins and Marusic2016) shows quantitative results based on the one-dimensional (1-D) coherence spectrum up to
$Re_{\unicode[STIX]{x1D70F}}=19\,000$
and observe that the footprint of the larger scales on the near-wall region remains. Particularly, the work of Baars et al. (Reference Baars, Hutchins and Marusic2016) shows quantitative results based on the one-dimensional (1-D) coherence spectrum up to
![]() $Re_{\unicode[STIX]{x1D70F}}=13\,300$
. These works supply evidence that the assumptions of the modelling methodologies herein developed would remain valid at considerably higher Reynolds numbers. Nevertheless, the footprint of the larger scales over the near-wall region and corresponding high coherence values are necessary ingredients for the use of the methods outlined in this work.
$Re_{\unicode[STIX]{x1D70F}}=13\,300$
. These works supply evidence that the assumptions of the modelling methodologies herein developed would remain valid at considerably higher Reynolds numbers. Nevertheless, the footprint of the larger scales over the near-wall region and corresponding high coherence values are necessary ingredients for the use of the methods outlined in this work.
4 Linear and nonlinear transfer functions

Figure 4. One-dimensional coherence (solid lines) overlaid on the one-dimensional pre-multiplied temporal spectrum as a function of the wall-normal direction for
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
and 8200. Coherence levels of 0.4 until 0.9 are highlighted.
$Re_{\unicode[STIX]{x1D703}}=4430$
and 8200. Coherence levels of 0.4 until 0.9 are highlighted.
4.1 Single-input linear transfer function
The basic supporting idea for the different identification methods that will be considered in this study is that there exists a function
![]() $f(I(z,t))$
that maps the relation between two wall-normal positions in the TBL, namely
$f(I(z,t))$
that maps the relation between two wall-normal positions in the TBL, namely
![]() $I(z,t)$
and
$I(z,t)$
and
![]() $O(z,t)$
. These two sets of data, taken along the spanwise direction and time, will be referred to as the input and output of the system, respectively. A qualitative description of such relation may be given in terms of the block diagram shown in figure 5. It should be noted that no restrictions have been made regarding the variables to be considered or the linearity of the function
$O(z,t)$
. These two sets of data, taken along the spanwise direction and time, will be referred to as the input and output of the system, respectively. A qualitative description of such relation may be given in terms of the block diagram shown in figure 5. It should be noted that no restrictions have been made regarding the variables to be considered or the linearity of the function
![]() $f$
.
$f$
.
The methods therefore assume the availability of spanwise- and time-resolved measurements, which are available in a numerical simulation but could be more difficult to obtain experimentally. Such turbulence measurements above the wall would require the use of time-resolved particle image velocimetry (PIV), such as in the work of Cuvier et al. (Reference Cuvier, Srinath, Stanislas, Foucaut, Laval, Kähler, Hain, Scharnowski, Schröder, Geisler, Agocs, Röse, Willert, Klinner, Amili, Atkinson and Soria2017). An alternative is to employ wall-shear stress sensors, as performed in closed-loop applications, such as in Lundell (Reference Lundell2007).
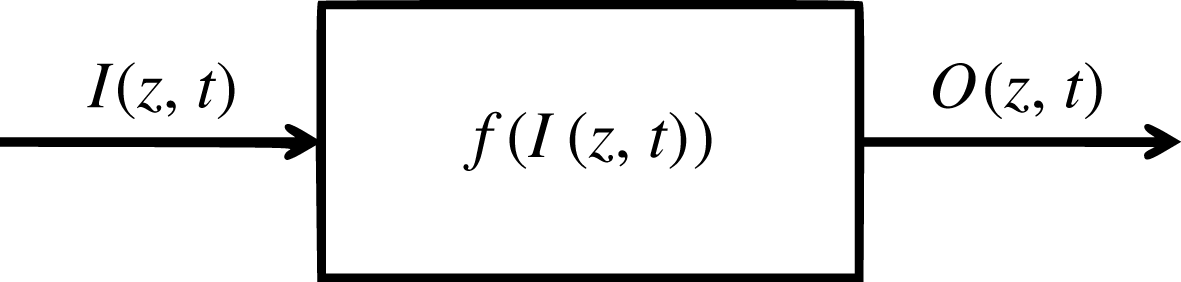
Figure 5. Block diagram describing the relationship between the input and output signals within the TBL.
The assumption in this section will be that there is a linear relationship between the two sets of measurements, such that the output may be predicted by means of a double convolution (along time and the spanwise direction) between the input measurement and a kernel,
which can be written in short as,
where
![]() $\otimes$
represents the double convolution. Here
$\otimes$
represents the double convolution. Here
![]() $g_{IO}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
is the convolution kernel, which, in accordance with the common nomenclature of the field, will be referred to as a transfer function in the remaining of this paper. The dummy variables
$g_{IO}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
is the convolution kernel, which, in accordance with the common nomenclature of the field, will be referred to as a transfer function in the remaining of this paper. The dummy variables
![]() $(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
, which are analogous to
$(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
, which are analogous to
![]() $(z,t)$
, were introduced for the calculation of the convolution. In order to obtain
$(z,t)$
, were introduced for the calculation of the convolution. In order to obtain
![]() $g_{IO}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
, the problem is formulated in the frequency/spanwise wavenumber space, where the optimal frequency response, in the least squares sense, may be defined from the auto- and cross-spectra of the input and output signals (Bendat & Piersol Reference Bendat and Piersol2011; Sasaki et al.
Reference Sasaki, Piantanida, Cavalieri and Jordan2017, Reference Sasaki, Morra, Fabbiane, Cavalieri, Hanifi and Henningson2018a
):
$g_{IO}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
, the problem is formulated in the frequency/spanwise wavenumber space, where the optimal frequency response, in the least squares sense, may be defined from the auto- and cross-spectra of the input and output signals (Bendat & Piersol Reference Bendat and Piersol2011; Sasaki et al.
Reference Sasaki, Piantanida, Cavalieri and Jordan2017, Reference Sasaki, Morra, Fabbiane, Cavalieri, Hanifi and Henningson2018a
):
where
![]() $S_{II}$
and
$S_{II}$
and
![]() $S_{IO}$
are the auto- and cross-spectra of the input and output, respectively. These quantities are calculated from the expected values of
$S_{IO}$
are the auto- and cross-spectra of the input and output, respectively. These quantities are calculated from the expected values of
![]() $\hat{\hat{I} }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\hat{\hat{I} }^{\ast }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})$
and
$\hat{\hat{I} }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\hat{\hat{I} }^{\ast }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})$
and
![]() $\hat{\hat{I} }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\hat{\hat{O} }^{\ast }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})$
, obtained from an ensemble averaging. The details of the method are outlined in appendix A. It should be noted that since the spanwise direction is periodic in the simulation, the ensemble averaging along this direction corresponds directly to the Fourier transform from
$\hat{\hat{I} }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\hat{\hat{O} }^{\ast }(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})$
, obtained from an ensemble averaging. The details of the method are outlined in appendix A. It should be noted that since the spanwise direction is periodic in the simulation, the ensemble averaging along this direction corresponds directly to the Fourier transform from
![]() $z$
to
$z$
to
![]() $\unicode[STIX]{x1D6FD}$
. Equation (4.3) is referred to as the
$\unicode[STIX]{x1D6FD}$
. Equation (4.3) is referred to as the
![]() $H_{1}$
estimator of the system (Rocklin, Crowley & Vold Reference Rocklin, Crowley and Vold1985), and it minimizes the error due to measurement noise in the output. Other formulations, such as the
$H_{1}$
estimator of the system (Rocklin, Crowley & Vold Reference Rocklin, Crowley and Vold1985), and it minimizes the error due to measurement noise in the output. Other formulations, such as the
![]() $H_{2}$
or
$H_{2}$
or
![]() $H_{\unicode[STIX]{x1D708}}$
estimators, exhibit different performances in terms of sensor noise minimization. They are, however, expected to perform equally well for this type of estimation, which does not consider the presence of measurement uncertainties.
$H_{\unicode[STIX]{x1D708}}$
estimators, exhibit different performances in terms of sensor noise minimization. They are, however, expected to perform equally well for this type of estimation, which does not consider the presence of measurement uncertainties.
One interesting property of the
![]() $H_{1}$
estimator is that it leads to a prediction error which is linearly uncorrelated with the input (Rocklin et al.
Reference Rocklin, Crowley and Vold1985; Bendat Reference Bendat1993). Consider the input/output relationship, given in the frequency–wavenumber domain,
$H_{1}$
estimator is that it leads to a prediction error which is linearly uncorrelated with the input (Rocklin et al.
Reference Rocklin, Crowley and Vold1985; Bendat Reference Bendat1993). Consider the input/output relationship, given in the frequency–wavenumber domain,
where
![]() $\unicode[STIX]{x1D716}$
will represent the error of the linear estimator. Post-multiplying equation (4.4) by the conjugate transpose of the input and taking the expected values, we obtain
$\unicode[STIX]{x1D716}$
will represent the error of the linear estimator. Post-multiplying equation (4.4) by the conjugate transpose of the input and taking the expected values, we obtain
Inserting the
![]() $H_{1}$
estimator of (4.3) leads to
$H_{1}$
estimator of (4.3) leads to
![]() $S_{\unicode[STIX]{x1D716},x}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})=0$
. Remaining correlated errors are related either to measurement noise, which can be considered negligible in this problem, or spectral leakage (Schoukens, Rolain & Pintelon Reference Schoukens, Rolain and Pintelon1997), which is minimized by use of long time series.
$S_{\unicode[STIX]{x1D716},x}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})=0$
. Remaining correlated errors are related either to measurement noise, which can be considered negligible in this problem, or spectral leakage (Schoukens, Rolain & Pintelon Reference Schoukens, Rolain and Pintelon1997), which is minimized by use of long time series.
Performing an inverse Fourier transform of
![]() $G_{IO}$
as:
$G_{IO}$
as:
where
![]() $\pm \unicode[STIX]{x1D6FD}_{n}$
represent the spanwise Nyquist wavenumbers calculated based on the spanwise discretization, leads to
$\pm \unicode[STIX]{x1D6FD}_{n}$
represent the spanwise Nyquist wavenumbers calculated based on the spanwise discretization, leads to
![]() $g_{IO}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
. This represents an empirical, linear, time-domain transfer function, which can be used to estimate the evolution of the fields separated in the wall-normal direction.
$g_{IO}(\unicode[STIX]{x1D701},\unicode[STIX]{x1D70F})$
. This represents an empirical, linear, time-domain transfer function, which can be used to estimate the evolution of the fields separated in the wall-normal direction.
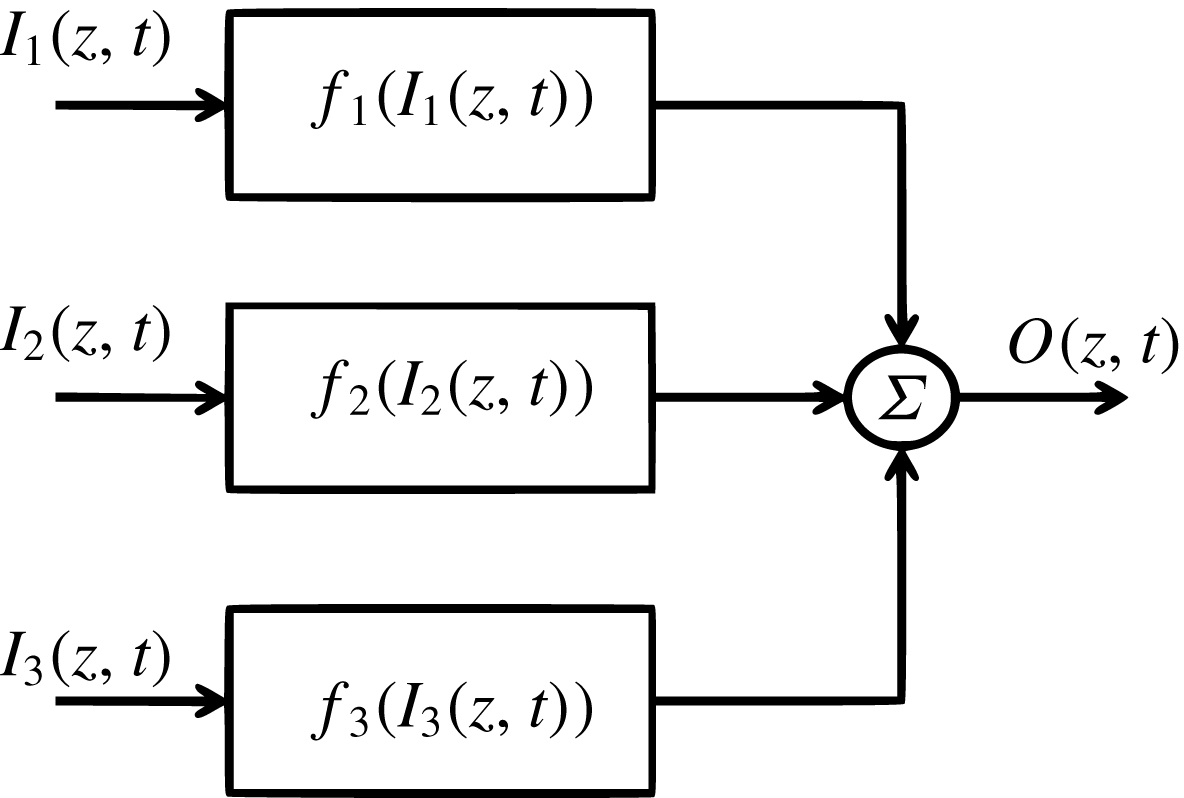
Figure 6. Block diagram describing the relationship between the multiple inputs and output of a system.
4.2 Multiple-input linear transfer function
In this section the construction of a model with multiple inputs will be introduced. This method applies to problems where multiple time series are available to be used in the estimation of the output. A qualitative schematic of the estimation is shown in the block diagram of figure 6. In this figure a system with three inputs is considered, however the extension to any number of inputs is straightforward. The linear hypothesis is inherent to this formulation since the output is assumed to be determined directly from the superposition of the contributions from each input,
![]() $I_{i}(z,t)$
, via the function
$I_{i}(z,t)$
, via the function
![]() $f_{i}(I_{i}(z,t))$
, which is estimated in terms of a convolution kernel,
$f_{i}(I_{i}(z,t))$
, which is estimated in terms of a convolution kernel,
![]() $g_{I_{i}O}$
. The estimation of the output is therefore obtained as follows:
$g_{I_{i}O}$
. The estimation of the output is therefore obtained as follows:
As in the case of the single-input problem, the transfer functions are found in the
![]() $(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
space and then inverse Fourier transformed to the physical domain. For a system with
$(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
space and then inverse Fourier transformed to the physical domain. For a system with
![]() $n$
inputs, the transfer functions are obtained from the solution of the linear system:
$n$
inputs, the transfer functions are obtained from the solution of the linear system:
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}S_{I_{1}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ S_{I_{2}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ \vdots \\ S_{I_{n}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\end{array}\right)=\left(\begin{array}{@{}cccc@{}}S_{I_{1}I_{1}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & S_{I_{1}I_{2}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & \ldots & S_{I_{1}I_{n}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ S_{I_{2}I_{1}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & S_{I_{2}I_{2}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & \ldots & S_{I_{2}I_{n}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ \vdots & \vdots & \ddots & \vdots \\ S_{I_{n}I_{1}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & S_{I_{n}I_{2}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & \ldots & S_{I_{n}I_{n}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\end{array}\right)\left(\begin{array}{@{}c@{}}G_{I_{1}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ G_{I_{2}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ \vdots \\ G_{I_{n}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}S_{I_{1}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ S_{I_{2}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ \vdots \\ S_{I_{n}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\end{array}\right)=\left(\begin{array}{@{}cccc@{}}S_{I_{1}I_{1}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & S_{I_{1}I_{2}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & \ldots & S_{I_{1}I_{n}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ S_{I_{2}I_{1}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & S_{I_{2}I_{2}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & \ldots & S_{I_{2}I_{n}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ \vdots & \vdots & \ddots & \vdots \\ S_{I_{n}I_{1}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & S_{I_{n}I_{2}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714}) & \ldots & S_{I_{n}I_{n}}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\end{array}\right)\left(\begin{array}{@{}c@{}}G_{I_{1}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ G_{I_{2}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\\ \vdots \\ G_{I_{n}O}(\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D714})\end{array}\right),\end{eqnarray}$$
which is performed for each frequency independently. The terms
![]() $S_{I_{i}O}$
define the cross-spectral density between the inputs and output, whereas
$S_{I_{i}O}$
define the cross-spectral density between the inputs and output, whereas
![]() $S_{I_{i}I_{j}}$
are the auto-spectral density of the inputs, when
$S_{I_{i}I_{j}}$
are the auto-spectral density of the inputs, when
![]() $i=j$
, or the cross-spectral density between different inputs, when
$i=j$
, or the cross-spectral density between different inputs, when
![]() $i\neq j$
. The auto- and cross-spectral densities are also calculated by means of ensemble averaging, as described in appendix A.
$i\neq j$
. The auto- and cross-spectral densities are also calculated by means of ensemble averaging, as described in appendix A.
Note that it could also be advantageous to deal with incoherent inputs, such that
![]() $S_{I_{i}I_{j}}=0$
if
$S_{I_{i}I_{j}}=0$
if
![]() $i\neq j$
, and only the diagonal terms in (4.8) remain. If the inputs are not correlated, each multiple-input–single-output (MISO) transfer function can be calculated directly as per (4.3),
$i\neq j$
, and only the diagonal terms in (4.8) remain. If the inputs are not correlated, each multiple-input–single-output (MISO) transfer function can be calculated directly as per (4.3),
![]() $G_{I_{i}O}=S_{I_{i}O}/S_{I_{i}I_{i}}$
, without the need to solve the matrix problem in (4.8). In order to decorrelate the inputs, the spectral conditioning technique (Bendat & Piersol Reference Bendat and Piersol2011) may be used. This has been used in all multiple-input cases studied here and the technique to do so is outlined in appendix B.
$G_{I_{i}O}=S_{I_{i}O}/S_{I_{i}I_{i}}$
, without the need to solve the matrix problem in (4.8). In order to decorrelate the inputs, the spectral conditioning technique (Bendat & Piersol Reference Bendat and Piersol2011) may be used. This has been used in all multiple-input cases studied here and the technique to do so is outlined in appendix B.
Each transfer function has to be inverse Fourier transformed, as per (4.6), in order to perform the estimation via the sum of convolutions in (4.7).
4.3 Nonlinear transfer function
Now we introduce the concept of nonlinear spectral analysis, via the use of nonlinear transfer functions, to the prediction of the interaction between the input and output signals. One of the few uses of nonlinear estimation methods in fluid mechanics may be found in the work of Naguib, Wark & Juckenhöfel (Reference Naguib, Wark and Juckenhöfel2001), who made use of stochastic estimation using nonlinear flow sources. On the other hand, nonlinear spectral analysis has been applied in previous works by means of a Volterra series to the derivation of nonlinear output frequency responses, with the objective of deriving properties of nonlinear systems (Guillaume, Pintelon & Schoukens Reference Guillaume, Pintelon and Schoukens1992; Lang & Billings Reference Lang and Billings1996; Peng, Lang & Billings Reference Peng, Lang and Billings2007). This technique assumes the expansion of the data into a power series, using an
![]() $N$
-integral kernel, leading to higher-order spectra. It presents drawbacks related both to the prohibiting computational demand, which limits the size of the system, and the large errors which can only be avoided with very large amounts of data.
$N$
-integral kernel, leading to higher-order spectra. It presents drawbacks related both to the prohibiting computational demand, which limits the size of the system, and the large errors which can only be avoided with very large amounts of data.
Here we will follow a somewhat different strategy, by considering a priori the existence of a nonlinear model between the defined input and output of the system and working on determining such model. The exact shape of the nonlinearities is unknown and they are sought with the objective of reproducing the observed behaviour. This method is thoroughly discussed in the works of Rice & Fitzpatrick (Reference Rice and Fitzpatrick1988, Reference Rice and Fitzpatrick1991) and Bendat (Reference Bendat1993), for time-dependent problems; in this study we extend the same ideas to application in a boundary layer with periodicity in the spanwise direction.
The nonlinear transfer-function technique considered here consists in replacing a single-input nonlinear system by a multiple-input linear system, where the linear identification techniques of the previous section may be applied. Consider a finite-memory, single-input–single-output nonlinear function
![]() $g(\cdot )$
, which acts on
$g(\cdot )$
, which acts on
![]() $I(z,t)$
, mapping it into the output
$I(z,t)$
, mapping it into the output
![]() $O(z,t)$
:
$O(z,t)$
:
as shown schematically in the block diagram of figure 7. Such nonlinear system may be represented by a superposition of linear and nonlinear operations performed on the input, as given by:
where
![]() $g_{i}$
represents an operation performed on the signal
$g_{i}$
represents an operation performed on the signal
![]() $I(z,t)$
and
$I(z,t)$
and
![]() $N_{TF}$
is the number of transfer functions considered. Each one of the nonlinear operators
$N_{TF}$
is the number of transfer functions considered. Each one of the nonlinear operators
![]() $g_{i}$
is now replaced by a nonlinear operator
$g_{i}$
is now replaced by a nonlinear operator
![]() $h_{i}$
and a linear operator
$h_{i}$
and a linear operator
![]() $A_{i}$
, such that:
$A_{i}$
, such that:
We now define the signal
![]() $\tilde{I_{i}}(O,t)$
, as the result of the nonlinear operation
$\tilde{I_{i}}(O,t)$
, as the result of the nonlinear operation
![]() $h_{i}$
applied to
$h_{i}$
applied to
![]() $I(O,t)$
. If all nonlinearities are encapsulated in the operators
$I(O,t)$
. If all nonlinearities are encapsulated in the operators
![]() $h_{i}$
, the resulting system may now be treated as having inputs
$h_{i}$
, the resulting system may now be treated as having inputs
![]() $\tilde{I} _{i}(O,t)$
and output
$\tilde{I} _{i}(O,t)$
and output
![]() $O(z,t)$
, such that linear frequency-domain techniques are applied to the determination of the convolution kernels
$O(z,t)$
, such that linear frequency-domain techniques are applied to the determination of the convolution kernels
![]() $A_{i}$
, in the same manner as derived in the previous section, for a multiple-input–single-output (MISO) problem. Figure 8 illustrates the steps in obtaining this new system on a sample case where three functions were considered in the determination of the output. Note that the extension to any number of input functions is straightforward.
$A_{i}$
, in the same manner as derived in the previous section, for a multiple-input–single-output (MISO) problem. Figure 8 illustrates the steps in obtaining this new system on a sample case where three functions were considered in the determination of the output. Note that the extension to any number of input functions is straightforward.
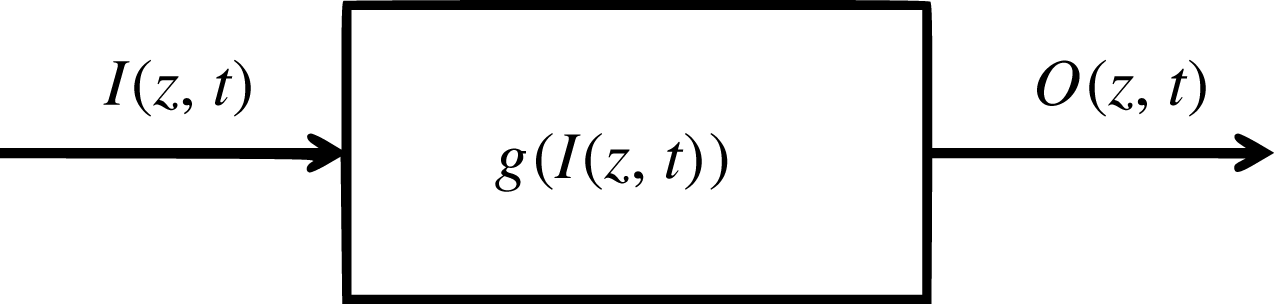
Figure 7. Block diagram corresponding to the nonlinear operation applied to
![]() $I(z,t)$
.
$I(z,t)$
.
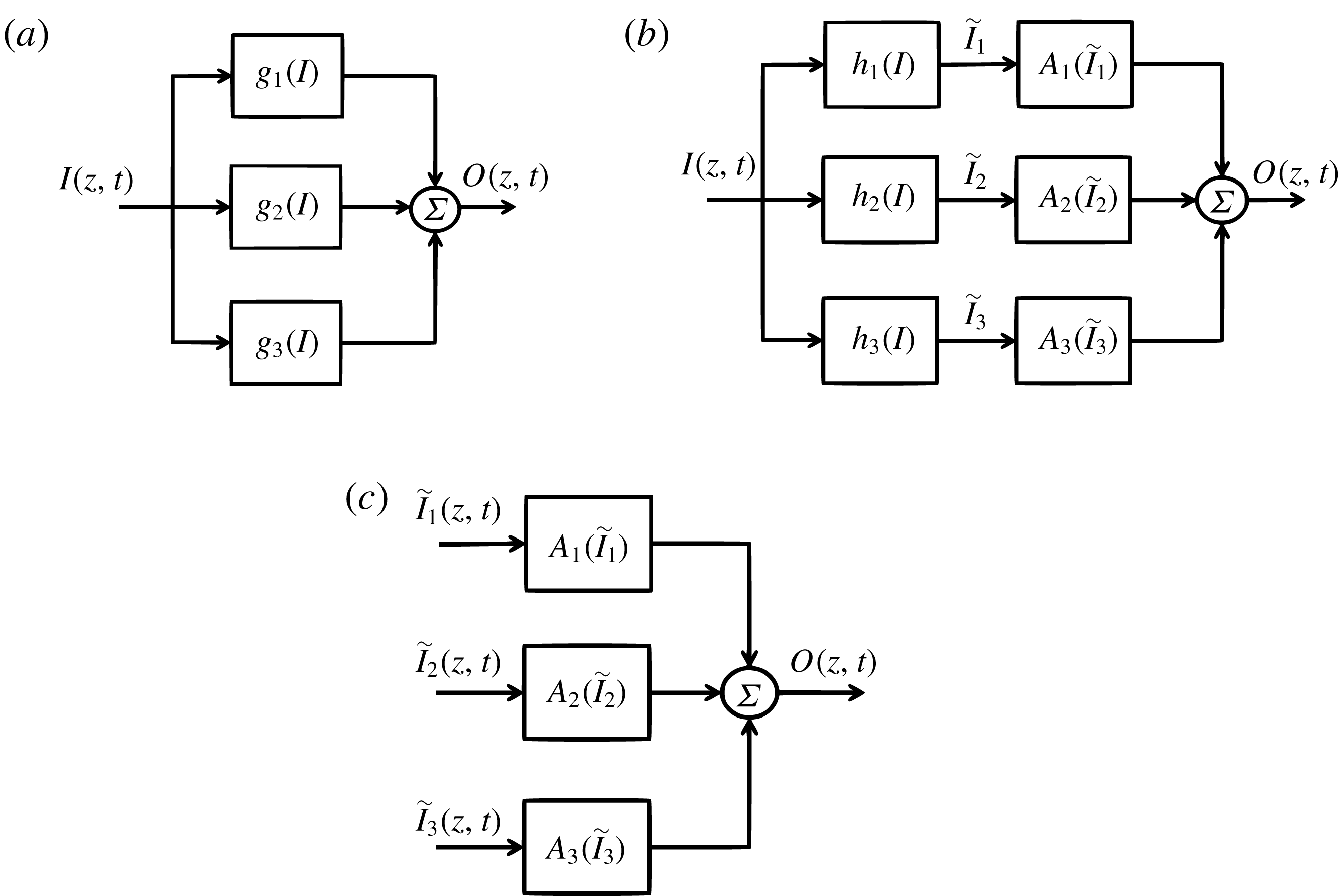
Figure 8. Summary of steps to transform a single-input nonlinear problem into a multiple-input linear system. (a) Nonlinear function is replaced by a sum of operations. (b) Each nonlinear function is broken into linear and nonlinear contributions. (c) The nonlinear operations are treated as known and the system is converted into the more usual MISO problem.
It should also be noted that when the exact shape of the nonlinearities is unknown, as will be the case here, the usual strategy is to deal with polynomial-like functions, with a degree sought such that a given performance is achieved; hence the method becomes more data driven than the previous approaches.
5 Results
Through this section the three methods for identification of the time/spanwise behaviour of the velocity fluctuations will be applied to the turbulent boundary layer of § 2. We will start with the simpler linear TF, then consider the case where more inputs are used to perform the estimation and, finally, consider the nonlinear transfer function. The performance of the three methods will be compared by using the pre-multiplied two-dimensional spectra.
The estimations will consider the streamwise velocity fluctuations as the output to be predicted and either streamwise velocity fluctuations or wall-shear stress as the input quantity. Nevertheless, the application to any other quantity is straightforward and demonstrated similar results as long as the same physical quantity was used as input and output (pressure, spanwise or wall-normal velocity fluctuations both as measured input and predicted quantity).
5.1 Linear transfer function
5.1.1 Sample predictions
In the results that follow, a sample prediction is considered, with the output (at
![]() $y^{+}=15$
), and an input at the lower edge of the log layer, at
$y^{+}=15$
), and an input at the lower edge of the log layer, at
![]() $y^{+}=50$
, for
$y^{+}=50$
, for
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
(
$Re_{\unicode[STIX]{x1D703}}=4430$
(
![]() $Re_{\unicode[STIX]{x1D70F}}=1324$
). For this case, the resulting transfer function, comparison of the time series and residual error are shown in figure 9.
$Re_{\unicode[STIX]{x1D70F}}=1324$
). For this case, the resulting transfer function, comparison of the time series and residual error are shown in figure 9.
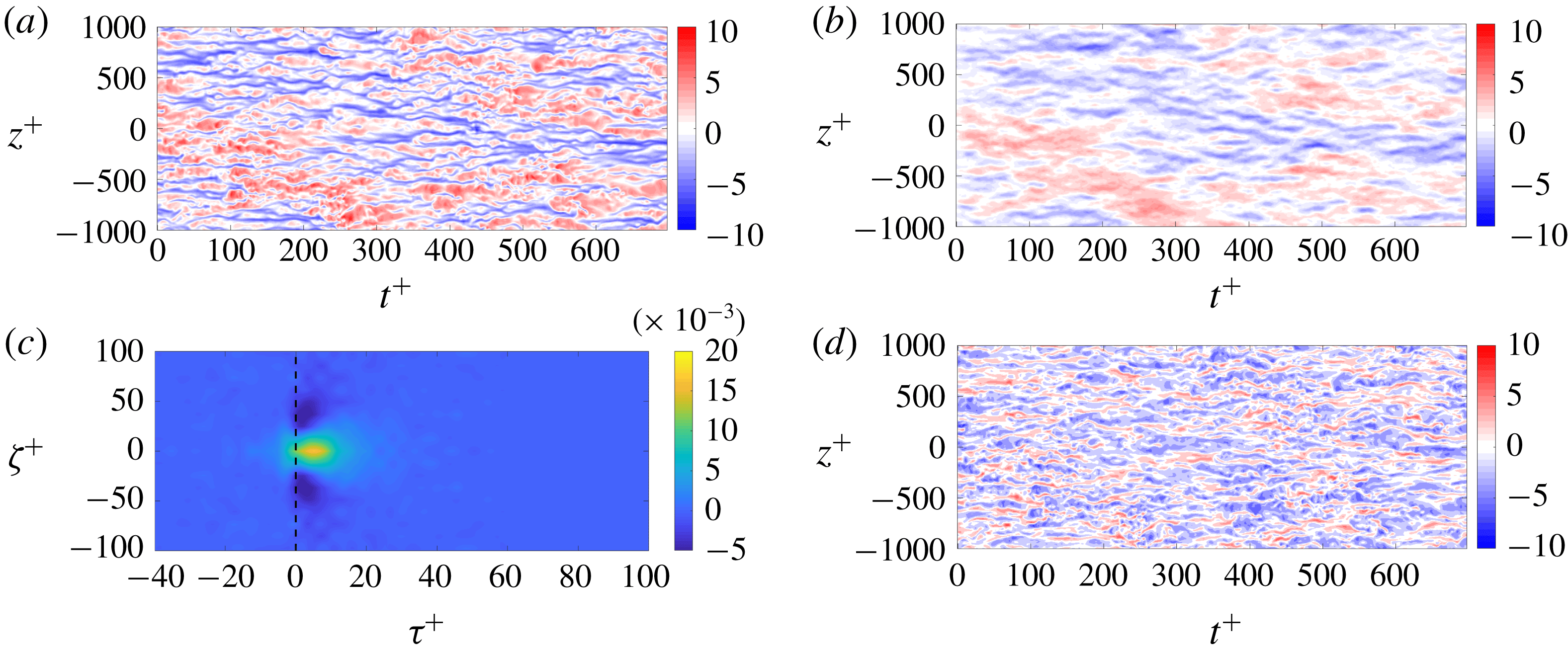
Figure 9. Comparison between LES data and estimated field, (a,b), for
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. The transfer function is shown in (c) and the error in the prediction (
$Re_{\unicode[STIX]{x1D703}}=4430$
. The transfer function is shown in (c) and the error in the prediction (
![]() $O_{LES}-O_{est}$
) in (d). In this case,
$O_{LES}-O_{est}$
) in (d). In this case,
![]() $y_{in}^{+}=50$
and
$y_{in}^{+}=50$
and
![]() $y_{out}^{+}=15$
and the prediction was made with the linear transfer function. (a) Instantaneous streamwise velocity fluctuation
$y_{out}^{+}=15$
and the prediction was made with the linear transfer function. (a) Instantaneous streamwise velocity fluctuation
![]() $u^{+}$
from the original LES dataset. (b) Instantaneous streamwise velocity fluctuation estimated via the linear transfer function approach from a measurement at
$u^{+}$
from the original LES dataset. (b) Instantaneous streamwise velocity fluctuation estimated via the linear transfer function approach from a measurement at
![]() $y_{in}^{+}=50$
. (c) Transfer function between input and output positions written in the spanwise and time coordinates. Dashed line highlights the zero time delay. (d) Residual from the single-input–single-output (SISO) linear prediction,
$y_{in}^{+}=50$
. (c) Transfer function between input and output positions written in the spanwise and time coordinates. Dashed line highlights the zero time delay. (d) Residual from the single-input–single-output (SISO) linear prediction,
![]() $u_{LES}^{+}-u_{est}^{+}$
.
$u_{LES}^{+}-u_{est}^{+}$
.
The resulting transfer function is mostly causal, i.e. its peak and most of its non-zero content is observed for
![]() $\unicode[STIX]{x1D70F}\geqslant 0$
. The transfer function can then be truncated for
$\unicode[STIX]{x1D70F}\geqslant 0$
. The transfer function can then be truncated for
![]() $\unicode[STIX]{x1D70F}<0$
without degrading the performance of the model such that the output in this case is obtained only with past measurements of the input, as the integral in (4.1) can be restricted to positive time delays
$\unicode[STIX]{x1D70F}<0$
without degrading the performance of the model such that the output in this case is obtained only with past measurements of the input, as the integral in (4.1) can be restricted to positive time delays
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
The time for the peak is related to the delay between the structures in the log layer and their footprint in the near-wall region. The physical interpretation of this is connected to the fact that the large-scale motions are not vertical, but inclined at an angle (Brown & Thomas Reference Brown and Thomas1977; Marusic & Heuer Reference Marusic and Heuer2007). This results in the observed delay between the measurement of the streamwise velocity at a higher wall-normal position and its effect near the wall, for the same cross-section in the streamwise direction, a feature previously observed in other works (Marusic et al. Reference Marusic, Mathis and Hutchins2010).
Figure 10. Resulting TF when the input is closer to the wall than the output,
![]() $y_{in}^{+}=15$
,
$y_{in}^{+}=15$
,
![]() $y_{out}^{+}=50$
, for
$y_{out}^{+}=50$
, for
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. Zero time delay and value of
$Re_{\unicode[STIX]{x1D703}}=4430$
. Zero time delay and value of
![]() $\unicode[STIX]{x0394}t^{+}$
considered in the estimation of the inclination angle of the structures are indicated by the dashed lines.
$\unicode[STIX]{x0394}t^{+}$
considered in the estimation of the inclination angle of the structures are indicated by the dashed lines.
It is also noticeable that the transfer function is capable of predicting the behaviour of the large-scale fluctuations of typical wavelength
![]() $\unicode[STIX]{x1D706}_{z}^{+}\approx 1000$
in this case, which are coherent along the wall-normal direction. The resulting pre-multiplied spectra for LES and estimated field, together with the prediction error, will be shown in figure 19 for the different methods evaluated in this work.
$\unicode[STIX]{x1D706}_{z}^{+}\approx 1000$
in this case, which are coherent along the wall-normal direction. The resulting pre-multiplied spectra for LES and estimated field, together with the prediction error, will be shown in figure 19 for the different methods evaluated in this work.
Via the use of the linear TF, the estimated field lacks the small-scale, higher-frequency fluctuations, which behave incoherently with measurements in the log layer. This is observed in the residual, as in figure 9, in the time domain. It may be observed that this error basically contains the fine-scale fluctuations, which would be present in the absence of an interaction with the larger scales, present in the outer layer. Although not shown, the resulting error is incoherent with the input signal at
![]() $y_{in}^{+}=50$
; thus such error could be related to the universal near-wall signal (Marusic et al.
Reference Marusic, Mathis and Hutchins2010).
$y_{in}^{+}=50$
; thus such error could be related to the universal near-wall signal (Marusic et al.
Reference Marusic, Mathis and Hutchins2010).
For illustration, the input and output positions are inverted, and the resulting transfer function is shown in figure 10. The behaviour becomes non-causal, as most of the non-zero content of the TF is for negative values. This is related to the aforementioned tilting of the structures in the wall-normal direction. Hence, the resulting model can only be used for data-reconstruction purposes, and real-time (on-line) predictions, and therefore closed-loop control, cannot be performed. This fact could of course be overcome by moving the input measurement upstream. Figures 9(c) and 10 also allow for an estimation of the tilting angle of the structures. Considering a vertical separation between input and measurement of
![]() $\unicode[STIX]{x0394}y^{+}=35$
, a delay of
$\unicode[STIX]{x0394}y^{+}=35$
, a delay of
![]() $\unicode[STIX]{x0394}t^{+}=9.4$
which is highlighted in figure 10 and a convective speed for the structures of
$\unicode[STIX]{x0394}t^{+}=9.4$
which is highlighted in figure 10 and a convective speed for the structures of
![]() $U_{c}^{+}=14$
, which is between the mean velocities at
$U_{c}^{+}=14$
, which is between the mean velocities at
![]() $y^{+}=15$
and
$y^{+}=15$
and
![]() $y^{+}=50$
(see figure 1), the resulting inclination angle is of
$y^{+}=50$
(see figure 1), the resulting inclination angle is of
![]() $14.9^{\circ }$
. This estimated value is in very good agreement with previous observations (Brown & Thomas Reference Brown and Thomas1977; Marusic & Heuer Reference Marusic and Heuer2007).
$14.9^{\circ }$
. This estimated value is in very good agreement with previous observations (Brown & Thomas Reference Brown and Thomas1977; Marusic & Heuer Reference Marusic and Heuer2007).
The results of this section are in accordance with the observations of Mathis et al. (Reference Mathis, Hutchins and Marusic2009, Reference Mathis, Hutchins and Marusic2011) and Marusic et al. (Reference Marusic, Mathis and Hutchins2010), where it is shown that the fluctuations present at higher wall-normal positions imprint their signature near the wall. The model proposed in these works is capable of instantaneous predictions of the large-scale fluctuations, by modelling the interactions with near-wall structures through a large-scale footprint, corresponding to a linear superposition, and amplitude modulation of near-wall streaks. The behaviour of the finer-scale fluctuations (error signal in figure 9) can then only be predicted statistically, by means of a proposed universal signal, which would be present in the absence of such interactions between the different scales in a turbulent boundary layer. The linear transfer function proposed in this work is capturing such superposition effect of the large-scale structures on the near-wall region.
In the following section, the performance of the method for other wall-normal positions and Reynolds numbers will be evaluated. The construction of transfer functions using input/output data at different streamwise positions, although feasible, will not be pursued here, given the available streamwise fields in the database, which present a high separation between each other. Nevertheless, for short distances, the streamwise separation between positions is expected to mostly alter the time delay for the peak of the transfer function.
5.1.2 Performance for different wall-normal positions and Reynolds numbers
In order to evaluate the dependence of the linear predictions on the distance from the wall, four inputs were considered,
![]() $y_{in}^{+}=50$
, 75, 100 and 200, for different values of
$y_{in}^{+}=50$
, 75, 100 and 200, for different values of
![]() $Re_{\unicode[STIX]{x1D703}}$
. Two metrics were used to compare the LES and the various predicted fields in a consistent manner, namely the variance of the velocity fluctuations and the normalized correlation between prediction and nonlinear simulation which, for this case, is defined as follows,
$Re_{\unicode[STIX]{x1D703}}$
. Two metrics were used to compare the LES and the various predicted fields in a consistent manner, namely the variance of the velocity fluctuations and the normalized correlation between prediction and nonlinear simulation which, for this case, is defined as follows,
 $$\begin{eqnarray}Corr=\frac{\displaystyle \int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\displaystyle \int _{-\infty }^{\infty }O_{LES}(t,z)O_{est}(t,z)\,\text{d}t\,\text{d}z}{\sqrt{\displaystyle \int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\displaystyle \int _{-\infty }^{\infty }O_{LES}^{2}(t,z)\,\text{d}t\,\text{d}z}\sqrt{\displaystyle \int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\displaystyle \int _{-\infty }^{\infty }O_{est}^{2}(t,z)\,\text{d}t\,\text{d}z}},\end{eqnarray}$$
$$\begin{eqnarray}Corr=\frac{\displaystyle \int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\displaystyle \int _{-\infty }^{\infty }O_{LES}(t,z)O_{est}(t,z)\,\text{d}t\,\text{d}z}{\sqrt{\displaystyle \int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\displaystyle \int _{-\infty }^{\infty }O_{LES}^{2}(t,z)\,\text{d}t\,\text{d}z}\sqrt{\displaystyle \int _{-\unicode[STIX]{x03C0}}^{\unicode[STIX]{x03C0}}\displaystyle \int _{-\infty }^{\infty }O_{est}^{2}(t,z)\,\text{d}t\,\text{d}z}},\end{eqnarray}$$
where
![]() $O_{LES}(t,z)$
and
$O_{LES}(t,z)$
and
![]() $O_{est}(t,z)$
are the LES and estimated fields, respectively. Note that this parameter varies between zero and unity, representing complete orthogonality and a perfect match between the two sets, respectively.
$O_{est}(t,z)$
are the LES and estimated fields, respectively. Note that this parameter varies between zero and unity, representing complete orthogonality and a perfect match between the two sets, respectively.
Figures 11 and 12 show the behaviour of the variance of the streamwise velocity and the correlations, respectively. Streamwise velocity was considered for both input and output. The predicted fields underestimate the value of the variances, which is in accordance with the fact that only the large structures, which exhibit a low frequency and wavenumber, are well captured by this method; the
![]() $H_{1}$
estimator leads to an output underpredicted by
$H_{1}$
estimator leads to an output underpredicted by
![]() $\unicode[STIX]{x1D6FE}$
, the coherence function defined in (3.1). One could also interpret the results of figure 11 as the amount of energy in the near-wall region which is due to the wall-connected eddies in the outer positions, given by their linear footprint into the smaller scale structures, which is significant, accounting for up to 45 % of the peak variance at
$\unicode[STIX]{x1D6FE}$
, the coherence function defined in (3.1). One could also interpret the results of figure 11 as the amount of energy in the near-wall region which is due to the wall-connected eddies in the outer positions, given by their linear footprint into the smaller scale structures, which is significant, accounting for up to 45 % of the peak variance at
![]() $y^{+}=15$
, for the highest Reynolds number and
$y^{+}=15$
, for the highest Reynolds number and
![]() $y_{in}^{+}=50$
, at the lower edge of the log layer.
$y_{in}^{+}=50$
, at the lower edge of the log layer.
Furthermore, the correlations exhibit relatively high values as long as input and output positions are close to each other. It is also noticeable that the performance of the model is fairly independent of the Reynolds number, at least for the evaluated cases, with the highest-
![]() $Re$
case slightly outperforming the other two. This may be due to the wider scale separation which is present in this case, and also to the more significant levels at outer positions for increasing Reynolds number, related to the outer peak seen in the spectra (Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011; Eitel-Amor et al.
Reference Eitel-Amor, Örlü and Schlatter2014). Finally, it is also noteworthy that even for the highest wall-normal positions under consideration the footprint of the fluctuations at these positions is still felt in the near-wall region, as shown in the correlation plots.
$Re$
case slightly outperforming the other two. This may be due to the wider scale separation which is present in this case, and also to the more significant levels at outer positions for increasing Reynolds number, related to the outer peak seen in the spectra (Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011; Eitel-Amor et al.
Reference Eitel-Amor, Örlü and Schlatter2014). Finally, it is also noteworthy that even for the highest wall-normal positions under consideration the footprint of the fluctuations at these positions is still felt in the near-wall region, as shown in the correlation plots.
Figure 13 shows a sample of the linear transfer functions, for the three evaluated Reynolds numbers, calculated between positions
![]() $y_{in}^{+}=50$
and
$y_{in}^{+}=50$
and
![]() $y_{out}^{+}=15$
. Note that the differences are mainly due to the amplitude and time delay to the maximum value, and are related to the fact that the interaction between wall-normal separated positions is slightly dependent on the Reynolds number of the flow. The information regarding the time delay for the peak comes directly from the inverse Fourier transform and
$y_{out}^{+}=15$
. Note that the differences are mainly due to the amplitude and time delay to the maximum value, and are related to the fact that the interaction between wall-normal separated positions is slightly dependent on the Reynolds number of the flow. The information regarding the time delay for the peak comes directly from the inverse Fourier transform and
![]() $t^{+}=tu_{\unicode[STIX]{x1D70F}}/l^{\ast }$
, with
$t^{+}=tu_{\unicode[STIX]{x1D70F}}/l^{\ast }$
, with
![]() $l^{\ast }=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
.
$l^{\ast }=\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}$
.
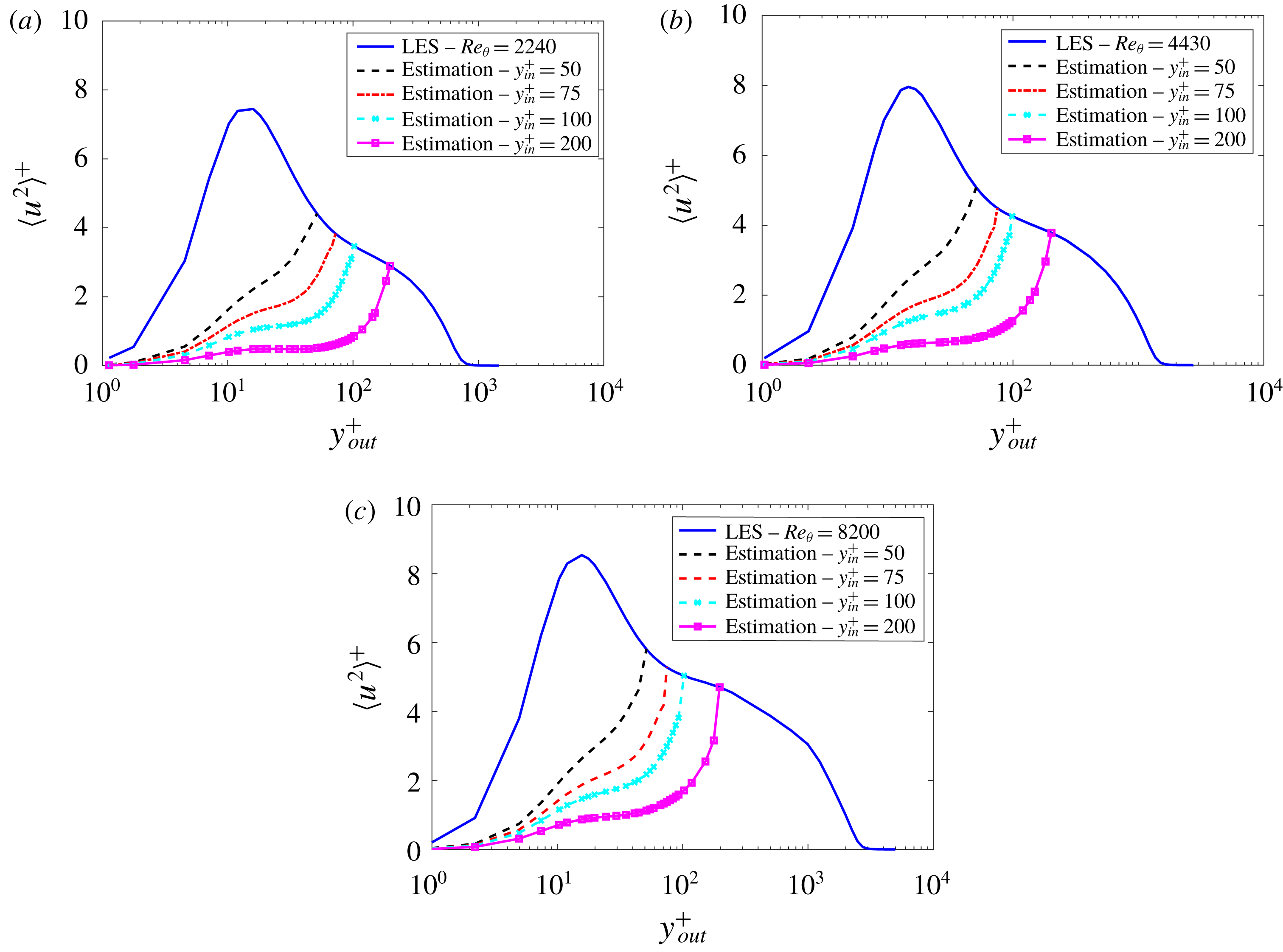
Figure 11. Comparison of the streamwise velocity variance of the estimated and LES fields for different input positions along the wall-normal direction at three Reynolds numbers. (a)
![]() $Re_{\unicode[STIX]{x1D703}}=2240$
. (b)
$Re_{\unicode[STIX]{x1D703}}=2240$
. (b)
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. (c)
$Re_{\unicode[STIX]{x1D703}}=4430$
. (c)
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
.
$Re_{\unicode[STIX]{x1D703}}=8200$
.
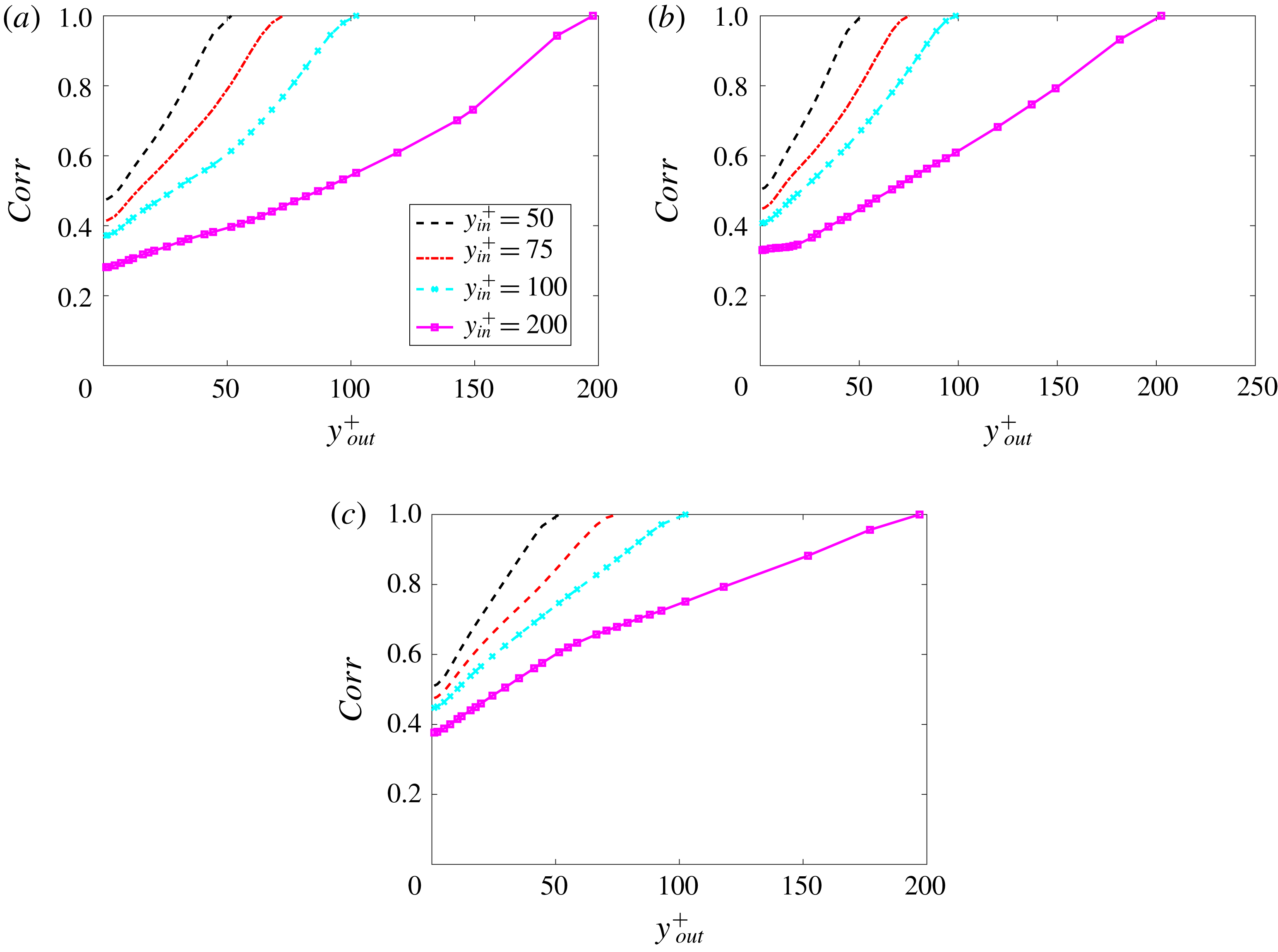
Figure 12. Correlation between estimated and LES fields for different positions along the wall-normal direction at three Reynolds numbers. Each curve corresponds to a fixed input position. (a)
![]() $Re_{\unicode[STIX]{x1D703}}=2240$
. (b)
$Re_{\unicode[STIX]{x1D703}}=2240$
. (b)
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. (c)
$Re_{\unicode[STIX]{x1D703}}=4430$
. (c)
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
.
$Re_{\unicode[STIX]{x1D703}}=8200$
.
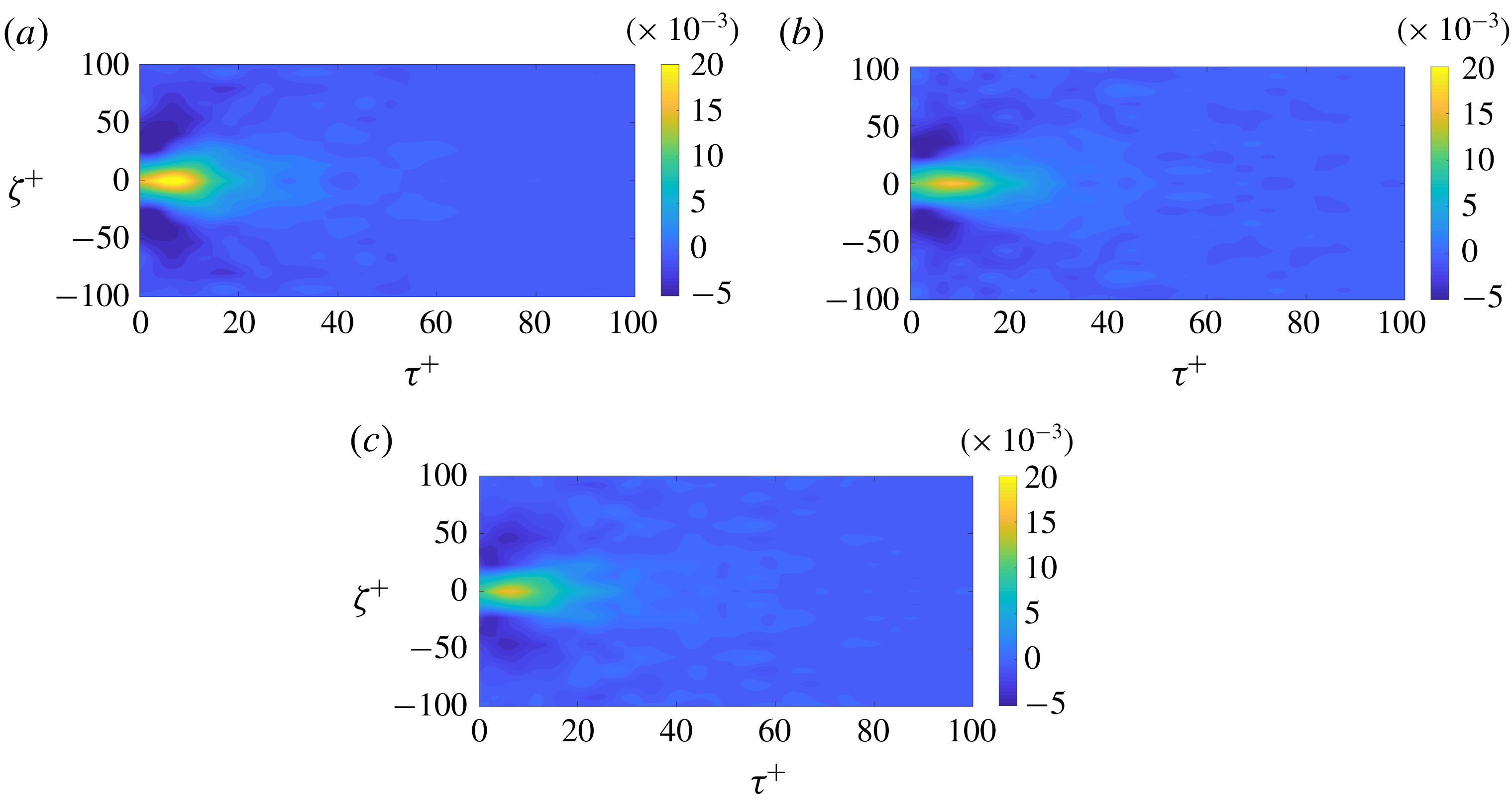
Figure 13. Behaviour of the linear transfer function for the three evaluated Reynolds numbers, for
![]() $y_{in}^{+}=50$
and
$y_{in}^{+}=50$
and
![]() $y_{out}^{+}=15$
. (a)
$y_{out}^{+}=15$
. (a)
![]() $Re_{\unicode[STIX]{x1D703}}=2240$
. (b)
$Re_{\unicode[STIX]{x1D703}}=2240$
. (b)
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. (c)
$Re_{\unicode[STIX]{x1D703}}=4430$
. (c)
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
.
$Re_{\unicode[STIX]{x1D703}}=8200$
.
5.1.3 An input on the wall
Results of the previous section allow us to extract the existing interaction between wall-normal separated positions. However, as highlighted in figure 3, the coherence between positions in the log layer and in the near-wall region lacks the fine scales, which is present when the input is considered on the wall. This is the main motivation for this section, which explores the flexibility of these empirically derived transfer functions to estimate higher wall-normal positions via a quantity potentially available in an experiment, namely the instantaneous wall-shear stress (see, for instance, Vinuesa & Örlü Reference Vinuesa, Örlü, Discetti and Ianiro2017). As a sample of the prediction, the streamwise velocity fluctuation will be considered as the output variable. As was the case for the previous models, instantaneous measurements of both input/output quantities are necessary only for the construction of the model.
Furthermore, the predictions considered here are based on non-causal transfer functions. This implies that they can be used in their present form only for data reconstruction. Their use for on-line (real-time) predictions would require the input measurement to be moved upstream of the output sensor. By doing so, a similar performance to the one shown here is expected.
The behaviour of the variance of the predicted fluctuations in comparison to the actual variance of the LES data and the correlations, calculated for the time-domain data (5.1) are shown in figure 14, using the wall-shear stress as the input quantity. A good performance is observed until
![]() $y^{+}\approx 10$
; above that position the variances start to be rapidly underestimated. A similar trend is also observed for the correlations, however they remain above 0.4 until
$y^{+}\approx 10$
; above that position the variances start to be rapidly underestimated. A similar trend is also observed for the correlations, however they remain above 0.4 until
![]() $y_{out}^{+}=250$
, which indicates that the footprint of the large-scale fluctuations present at this position is still felt on the near-wall region. Only the phase of the fluctuations can still be fairly well predicted, their amplitude, on the other hand, is highly underestimated, which account for the large discrepancy observed in the variances at this region.
$y_{out}^{+}=250$
, which indicates that the footprint of the large-scale fluctuations present at this position is still felt on the near-wall region. Only the phase of the fluctuations can still be fairly well predicted, their amplitude, on the other hand, is highly underestimated, which account for the large discrepancy observed in the variances at this region.
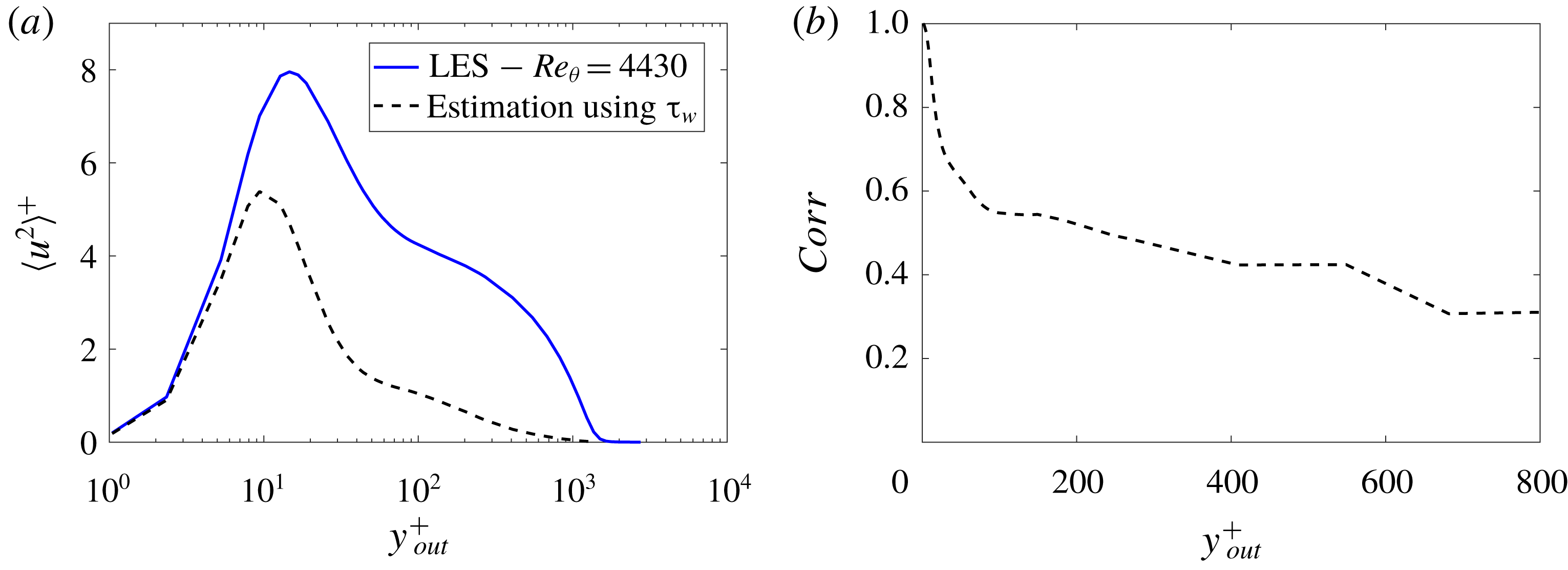
Figure 14. Performance metrics for the predicted field in comparison to the LES data, for the
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
case, using wall shear as input and the linear TF. (a) Variance of predicted and LES fields. (b) Correlation between predicted and LES fields.
$Re_{\unicode[STIX]{x1D703}}=4430$
case, using wall shear as input and the linear TF. (a) Variance of predicted and LES fields. (b) Correlation between predicted and LES fields.
The resulting pre-multiplied spectrum at position
![]() $y^{+}=15$
is shown below in figure 19, and the corresponding error in comparison to the actual LES data in figure 20. It may be observed that the location of the peak in the spectrum is well determined, although its magnitude is underestimated. The better performance obtained when the input
$y^{+}=15$
is shown below in figure 19, and the corresponding error in comparison to the actual LES data in figure 20. It may be observed that the location of the peak in the spectrum is well determined, although its magnitude is underestimated. The better performance obtained when the input
![]() $y_{in}^{+}$
is considered as the wall-shear stress rather than the streamwise velocity in the outer layer is related to the fact that the fluctuations are coherent within the near-wall region.
$y_{in}^{+}$
is considered as the wall-shear stress rather than the streamwise velocity in the outer layer is related to the fact that the fluctuations are coherent within the near-wall region.
5.2 Multiple-input transfer function
As shown in § 5.1, the performance of the predictions decays as the distance between input and output positions is increased. In this subsection, we try to diminish such effect by considering the multiple-input–single-output (MISO) transfer function, where one input is located at the wall, given in terms of shear measurements (i.e. wall-shear stress), and the other is at
![]() $y^{+}=50$
,
$y^{+}=50$
,
![]() $y^{+}=100$
or
$y^{+}=100$
or
![]() $y^{+}=200$
. We also consider the case with four inputs, at the wall and at
$y^{+}=200$
. We also consider the case with four inputs, at the wall and at
![]() $y^{+}=50$
, 100 and 200. As before, the transfer functions present non-causal values when the input is closer to the wall than the output, which would have to be compensated for real-time implementations by means of offsets in the streamwise separation.
$y^{+}=50$
, 100 and 200. As before, the transfer functions present non-causal values when the input is closer to the wall than the output, which would have to be compensated for real-time implementations by means of offsets in the streamwise separation.
Two metrics will be used to evaluate the performance of the transfer functions: the streamwise velocity variance and the correlation between estimated and LES data, which are given in figure 15, for the case of
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. Analogous results are also obtained for
$Re_{\unicode[STIX]{x1D703}}=4430$
. Analogous results are also obtained for
![]() $Re_{\unicode[STIX]{x1D703}}=2240$
and 8200, (not shown). The use of a multiple-input TF with different flow quantities (e.g. streamwise and wall-normal velocity fluctuations) was also assessed, however it did not improve the performance of the predictions and will therefore not be shown here, for the sake of brevity. The use of multiple inputs considerably increases the performance of the predictive model, indicating that inputs on and above the wall are complementary in terms of the information they add to the resulting field. In particular, for the case with four inputs, the correlations between prediction and reference data remain above 70 % from
$Re_{\unicode[STIX]{x1D703}}=2240$
and 8200, (not shown). The use of a multiple-input TF with different flow quantities (e.g. streamwise and wall-normal velocity fluctuations) was also assessed, however it did not improve the performance of the predictions and will therefore not be shown here, for the sake of brevity. The use of multiple inputs considerably increases the performance of the predictive model, indicating that inputs on and above the wall are complementary in terms of the information they add to the resulting field. In particular, for the case with four inputs, the correlations between prediction and reference data remain above 70 % from
![]() $y_{out}^{+}=180$
until the wall. The pre-multiplied spectra of the predicted and LES fields are shown below in figure 19, at the output position of
$y_{out}^{+}=180$
until the wall. The pre-multiplied spectra of the predicted and LES fields are shown below in figure 19, at the output position of
![]() $y^{+}=15$
, using a MISO TF with two inputs (namely the velocity fluctuations at
$y^{+}=15$
, using a MISO TF with two inputs (namely the velocity fluctuations at
![]() $y_{in}^{+}=50$
and the wall-shear stress). The performance of the MISO prediction is significantly improved from the single-input cases, with a good prediction of the main features of the pre-multiplied spectrum.
$y_{in}^{+}=50$
and the wall-shear stress). The performance of the MISO prediction is significantly improved from the single-input cases, with a good prediction of the main features of the pre-multiplied spectrum.
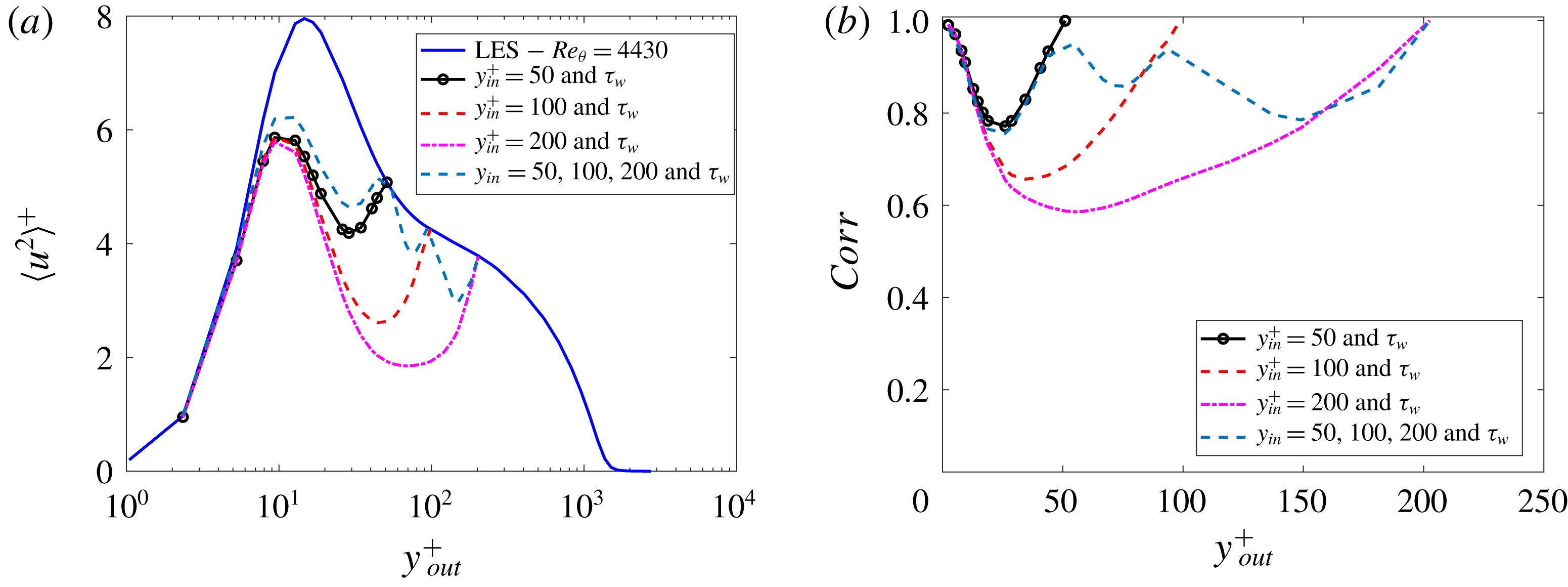
Figure 15. Performance metrics for the predicted field, using the MISO transfer functions, in comparison to the LES data. The inputs in the outer layer were
![]() $y^{+}=50$
,
$y^{+}=50$
,
![]() $y^{+}=100$
and
$y^{+}=100$
and
![]() $y^{+}=150$
. (a) Variance of predicted and LES fields. (b) Correlation between predicted and LES fields.
$y^{+}=150$
. (a) Variance of predicted and LES fields. (b) Correlation between predicted and LES fields.
5.3 Nonlinear transfer functions
In this section, the method of nonlinear spectral analysis will be considered in order to try to further improve the performance of the estimations. A single input will be considered, located at the wall, using wall-shear stress. The results will concern the
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
case, however similar observations were also made for the other Reynolds numbers. The output to be estimated was taken as the streamwise velocity fluctuation. Polynomial nonlinearities will be considered as follows:
$Re_{\unicode[STIX]{x1D703}}=4430$
case, however similar observations were also made for the other Reynolds numbers. The output to be estimated was taken as the streamwise velocity fluctuation. Polynomial nonlinearities will be considered as follows:
such that for
![]() $N_{TF}=1$
, the linear case is recovered, and for this particular case,
$N_{TF}=1$
, the linear case is recovered, and for this particular case,
![]() $N_{TF}$
will coincide with the highest polynomial order of the transfer function. The evaluation of the number of terms to be used in the series is made in terms of error metrics defined in the time domain, correlations between estimated and LES fields and relative mean values of the error,
$N_{TF}$
will coincide with the highest polynomial order of the transfer function. The evaluation of the number of terms to be used in the series is made in terms of error metrics defined in the time domain, correlations between estimated and LES fields and relative mean values of the error,
 $$\begin{eqnarray}e_{MS}[\%]=\frac{\displaystyle \int _{-z_{max}/2}^{z_{max}/2}\displaystyle \int _{0}^{t_{max}}(u_{est}^{+}-u_{LES}^{+})^{2}\,\text{d}t\,\text{d}z}{\displaystyle \int _{-z_{max}/2}^{z_{max}/2}\displaystyle \int _{0}^{t_{max}}(u_{est}^{+})^{2}\,\text{d}t\,\text{d}z}\times 100.\end{eqnarray}$$
$$\begin{eqnarray}e_{MS}[\%]=\frac{\displaystyle \int _{-z_{max}/2}^{z_{max}/2}\displaystyle \int _{0}^{t_{max}}(u_{est}^{+}-u_{LES}^{+})^{2}\,\text{d}t\,\text{d}z}{\displaystyle \int _{-z_{max}/2}^{z_{max}/2}\displaystyle \int _{0}^{t_{max}}(u_{est}^{+})^{2}\,\text{d}t\,\text{d}z}\times 100.\end{eqnarray}$$
Error metrics in the spectral domain will be obtained by calculating the two-dimensional spectrum of the error,
![]() $E_{ee}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})=\langle \hat{\hat{e}}\hat{\hat{e}}^{\ast }\rangle$
, where
$E_{ee}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})=\langle \hat{\hat{e}}\hat{\hat{e}}^{\ast }\rangle$
, where
and determining the relative error at the near-wall peak (
![]() $err_{peak}$
) and the relative mean error,
$err_{peak}$
) and the relative mean error,
 $$\begin{eqnarray}err_{mean}[\%]=\frac{\displaystyle \int _{\unicode[STIX]{x1D6FD}_{1}}^{\unicode[STIX]{x1D6FD}_{2}}\displaystyle \int _{\unicode[STIX]{x1D714}_{1}}^{\unicode[STIX]{x1D714}_{2}}E_{ee}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\unicode[STIX]{x1D6FD}}{\displaystyle \int _{\unicode[STIX]{x1D6FD}_{1}}^{\unicode[STIX]{x1D6FD}_{2}}\displaystyle \int _{\unicode[STIX]{x1D714}_{1}}^{\unicode[STIX]{x1D714}_{2}}E_{uu}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\unicode[STIX]{x1D6FD}}\times 100\end{eqnarray}$$
$$\begin{eqnarray}err_{mean}[\%]=\frac{\displaystyle \int _{\unicode[STIX]{x1D6FD}_{1}}^{\unicode[STIX]{x1D6FD}_{2}}\displaystyle \int _{\unicode[STIX]{x1D714}_{1}}^{\unicode[STIX]{x1D714}_{2}}E_{ee}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\unicode[STIX]{x1D6FD}}{\displaystyle \int _{\unicode[STIX]{x1D6FD}_{1}}^{\unicode[STIX]{x1D6FD}_{2}}\displaystyle \int _{\unicode[STIX]{x1D714}_{1}}^{\unicode[STIX]{x1D714}_{2}}E_{uu}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})\,\text{d}\unicode[STIX]{x1D714}\,\text{d}\unicode[STIX]{x1D6FD}}\times 100\end{eqnarray}$$
all of which are indices relevant for closed-loop control applications. The variance of the prediction will also be observed, as a complementary metric.
Figure 16 shows the defined error metrics as a function of the number of terms used in the definition of the nonlinear TF, until
![]() $N_{TF}=20$
. The output is located at
$N_{TF}=20$
. The output is located at
![]() $y_{out}^{+}=15$
. There is a slight improvement when a quadratic term is used for the prediction. The correlations are increased from 0.79 to 0.84, the error decreases from 36 to 31 % and the value of the inner wall peak improves from 4.9 to 5.9. The peak error in the spectral domain decreases from 27 to 20 % and the mean error from 42 to 36 %. However, the addition of more terms, beyond the quadratic estimation, causes the predicted field to be less accurate in the time domain, as the correlation decreases and the error worsens. Although not shown, the same trend is observed for other output positions within the buffer layer, an improvement in the predicted field when a quadratic term is considered in the series. We therefore proceed by truncating the nonlinear analysis at the quadratic term.
$y_{out}^{+}=15$
. There is a slight improvement when a quadratic term is used for the prediction. The correlations are increased from 0.79 to 0.84, the error decreases from 36 to 31 % and the value of the inner wall peak improves from 4.9 to 5.9. The peak error in the spectral domain decreases from 27 to 20 % and the mean error from 42 to 36 %. However, the addition of more terms, beyond the quadratic estimation, causes the predicted field to be less accurate in the time domain, as the correlation decreases and the error worsens. Although not shown, the same trend is observed for other output positions within the buffer layer, an improvement in the predicted field when a quadratic term is considered in the series. We therefore proceed by truncating the nonlinear analysis at the quadratic term.
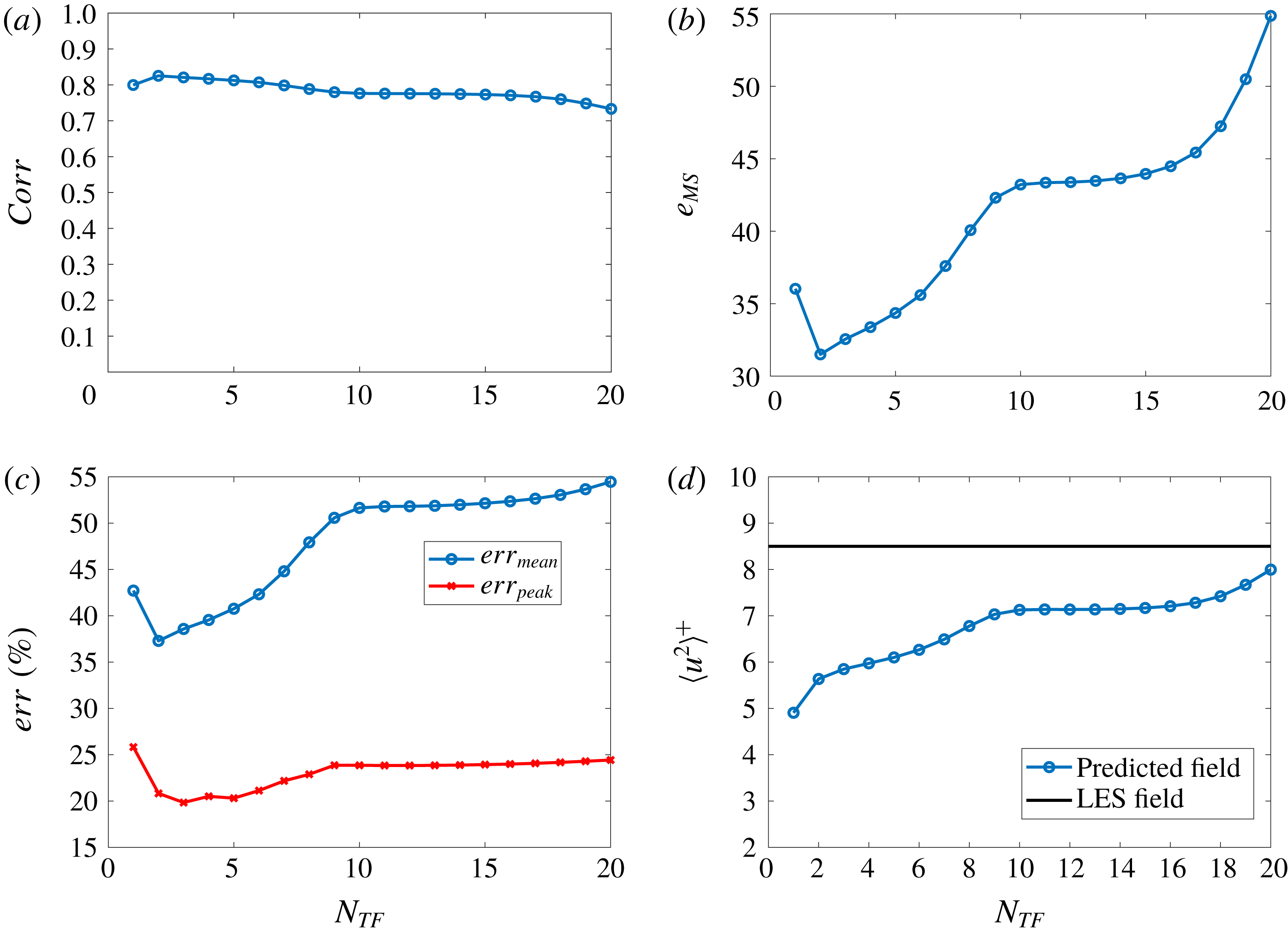
Figure 16. Behaviour of the error calculated in the time and frequency domains and variance of the predicted field as a function of the number of terms used in the nonlinear transfer function. (a) Correlation between prediction and LES. (b) Mean square value of the error. (c) Spectral error metrics. (d) Variance of the predicted field.
The behaviour of the prediction and the residual in the
![]() $(t,z)$
domain is shown in figure 17 and demonstrates an improvement with respect to the linear case, particularly regarding the amplitude of the predicted field. The relative mean error, defined as per (5.3) diminishes from 27 to 20 %, from the linear to the nonlinear case, respectively. Analogously to the linear case, in order to better assess the method, the accuracy of the prediction was evaluated as a function of the wall-normal distance. This is shown in figure 18, in terms of the correlation between predicted and LES fields and the corresponding variances. The result is overlaid to the linear case, to better highlight the differences. Up to
$(t,z)$
domain is shown in figure 17 and demonstrates an improvement with respect to the linear case, particularly regarding the amplitude of the predicted field. The relative mean error, defined as per (5.3) diminishes from 27 to 20 %, from the linear to the nonlinear case, respectively. Analogously to the linear case, in order to better assess the method, the accuracy of the prediction was evaluated as a function of the wall-normal distance. This is shown in figure 18, in terms of the correlation between predicted and LES fields and the corresponding variances. The result is overlaid to the linear case, to better highlight the differences. Up to
![]() $y_{out}^{+}\approx 30$
, the nonlinear method exhibits slightly higher correlations with the actual LES data, with a significant improvement of the variances, indicating that the amplitude is better captured by this strategy. As the output is moved above the buffer layer, the nonlinear strategy does not lead to improvements of the predicted field.
$y_{out}^{+}\approx 30$
, the nonlinear method exhibits slightly higher correlations with the actual LES data, with a significant improvement of the variances, indicating that the amplitude is better captured by this strategy. As the output is moved above the buffer layer, the nonlinear strategy does not lead to improvements of the predicted field.

Figure 17. Behaviour of the prediction in the
![]() $(t,z)$
domain, input at wall using wall-shear stress and output at
$(t,z)$
domain, input at wall using wall-shear stress and output at
![]() $y_{out}=15$
. (a) LES data. (b) Linear prediction. (c) Nonlinear prediction with the linear and quadratic terms. (d) Residual,
$y_{out}=15$
. (a) LES data. (b) Linear prediction. (c) Nonlinear prediction with the linear and quadratic terms. (d) Residual,
![]() $u_{est}^{+}-u_{LES}^{+}$
with the linear method. (e) Residual,
$u_{est}^{+}-u_{LES}^{+}$
with the linear method. (e) Residual,
![]() $u_{est}^{+}-u_{LES}^{+}$
with the nonlinear method.
$u_{est}^{+}-u_{LES}^{+}$
with the nonlinear method.
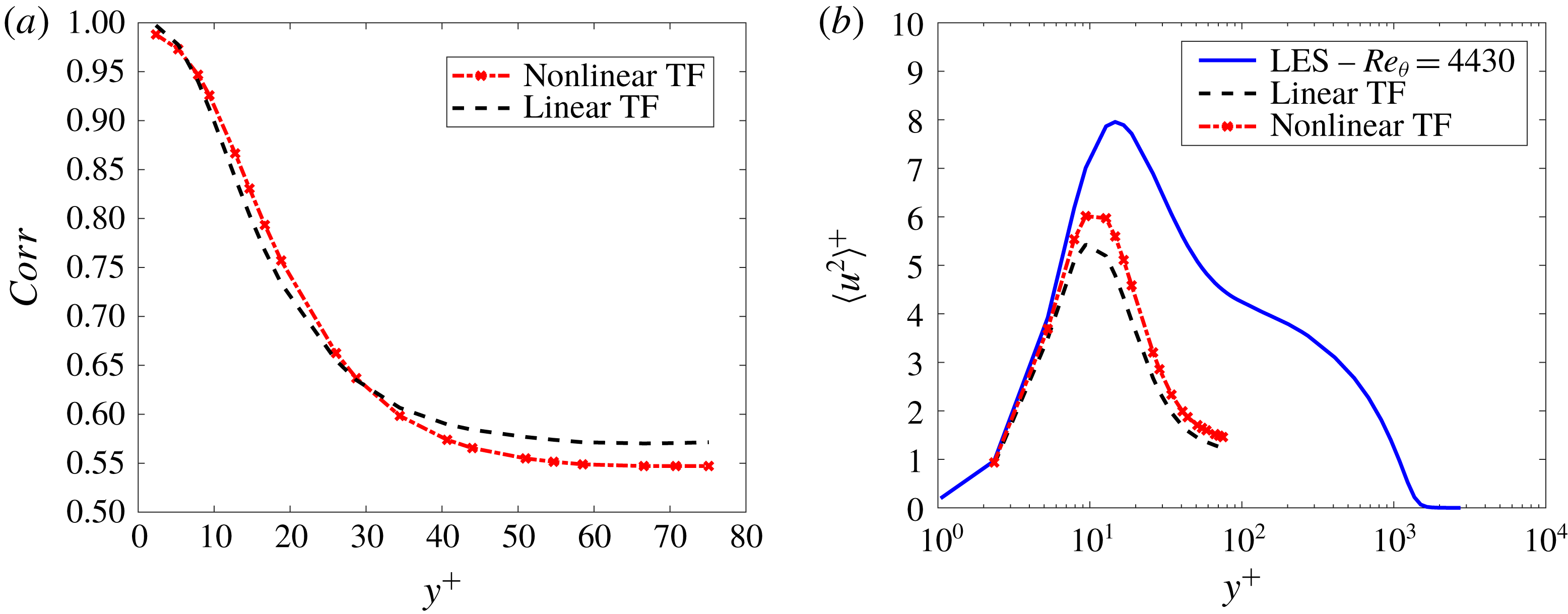
Figure 18. Performance of the nonlinear prediction as a function of the wall-normal direction, results are compared to the linear case. (a) Correlation between prediction and LES. (b) Variances of the predicted and LES streamwise velocity fluctuation.
Application of the nonlinear spectral analysis with an input measurement above the buffer layer did not improve the prediction in the time domain. This indicates that the footprint of the larger scales on the near-wall region is predominantly a linear superposition phenomenon, which is being captured by the linear transfer function approach. Although not shown, the quadratic term of the shear-stress input presents a mild coherence with the output signal, which justifies for its improvement in the prediction. Such improvement with a quadratic term had first been observed by Naguib et al. (Reference Naguib, Wark and Juckenhöfel2001), who attributed such characteristic to a turbulent–turbulent interaction, and observed that the quadratic term tends to scale in outer units.
5.4 Comparison of the methods and discussion
We start by computing the two-dimensional pre-multiplied spectra of predictions obtained by the different approaches. The output is located at
![]() $y_{out}^{+}=15$
, corresponding to the near-wall peak. One, two or four inputs are considered: at the wall, i.e. using the wall-shear stress, and at
$y_{out}^{+}=15$
, corresponding to the near-wall peak. One, two or four inputs are considered: at the wall, i.e. using the wall-shear stress, and at
![]() $y_{in}^{+}=50$
,
$y_{in}^{+}=50$
,
![]() $y_{in}^{+}=100$
and
$y_{in}^{+}=100$
and
![]() $y_{in}^{+}=200$
. The resulting spectra are shown in figure 19 for the different approaches considered in this work, in comparison to the actual LES data.
$y_{in}^{+}=200$
. The resulting spectra are shown in figure 19 for the different approaches considered in this work, in comparison to the actual LES data.
Figure 19. Comparison of inner-scaled pre-multiplied two-dimensional spectra from the linear and nonlinear predictions with the LES field at
![]() $y^{+}=15$
, for the
$y^{+}=15$
, for the
![]() $Re_{\unicode[STIX]{x1D703}}=4430$
. The crosses correspond to reference locations for the inner (
$Re_{\unicode[STIX]{x1D703}}=4430$
. The crosses correspond to reference locations for the inner (
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
![]() $(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
$(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). (a) LES data. (b) Linear transfer function using
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). (a) LES data. (b) Linear transfer function using
![]() $y^{+}=50$
as input. (c) MISO transfer function using
$y^{+}=50$
as input. (c) MISO transfer function using
![]() $y_{in}^{+}=50$
and wall-shear stress. (d) MISO transfer function using
$y_{in}^{+}=50$
and wall-shear stress. (d) MISO transfer function using
![]() $y_{in}^{+}=50$
,
$y_{in}^{+}=50$
,
![]() $y_{in}^{+}=100$
,
$y_{in}^{+}=100$
,
![]() $y_{in}^{+}=200$
and wall-shear stress. (e) Linear transfer function using wall-shear stress. (f) Nonlinear transfer function using wall-shear stress.
$y_{in}^{+}=200$
and wall-shear stress. (e) Linear transfer function using wall-shear stress. (f) Nonlinear transfer function using wall-shear stress.
In order to better assess the results, we will consider the two-dimensional pre-multiplied spectra of the residual error. This metric supplies information concerning the instantaneous accuracy of the prediction, an important information for active control applications. The result is shown in figure 20. The linear TF based on an input on the outer layer leads to a significant error in the prediction of the near-wall peak, as only the large-scale structures are coherent between these positions. The accuracy of the determination of the near-wall data is significantly improved when wall-shear data are used, either in the SISO or MISO applications, as the near-wall cycle maintains significant coherence down to the wall.
Figure 20. Pre-multiplied two-dimensional spectra of the error calculated between predicted and LES streamwise velocity fields. The limits of the colour bar were kept as those of the reference data, in order to facilitate the comparison. The crosses correspond to reference locations for the inner (
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (100,100)$
) and outer peaks (
![]() $(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
$(\unicode[STIX]{x1D706}_{t},\unicode[STIX]{x1D706}_{z})\approx (10\unicode[STIX]{x1D6FF}_{99}/U_{\infty },\unicode[STIX]{x1D6FF}_{99})$
,
![]() $(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). (a) Linear transfer function using
$(\unicode[STIX]{x1D706}_{t}^{+},\unicode[STIX]{x1D706}_{z}^{+})\approx (1400,1300)$
). (a) Linear transfer function using
![]() $y^{+}=50$
as input. (b) MISO transfer function using
$y^{+}=50$
as input. (b) MISO transfer function using
![]() $y_{in}^{+}=50$
and wall-shear stress. (c) MISO transfer function using
$y_{in}^{+}=50$
and wall-shear stress. (c) MISO transfer function using
![]() $y_{in}^{+}=50$
,
$y_{in}^{+}=50$
,
![]() $y_{in}^{+}=100$
,
$y_{in}^{+}=100$
,
![]() $y_{in}^{+}=200$
and wall-shear stress. (d) Linear transfer function using walls-shear stress as input. (e) Nonlinear transfer function using wall-shear stress.
$y_{in}^{+}=200$
and wall-shear stress. (d) Linear transfer function using walls-shear stress as input. (e) Nonlinear transfer function using wall-shear stress.
Four additional metrics will be considered to compare the predictions of the three methods at
![]() $y_{out}^{+}=15$
: the correlation coefficient (5.1), the relative mean error
$y_{out}^{+}=15$
: the correlation coefficient (5.1), the relative mean error
![]() $e_{MS}$
between predicted and reference fields (5.3), the relative error in the determination of the value of the peak and the relative mean error in the determination of the spectra, both of which can be obtained by the two-dimensional pre-multiplied spectra of the error in figure 20. It should be noted that all of these metrics are related to the ability of the methods to capture the unsteady behaviour of the fluctuations, rather than only the turbulence statistics.
$e_{MS}$
between predicted and reference fields (5.3), the relative error in the determination of the value of the peak and the relative mean error in the determination of the spectra, both of which can be obtained by the two-dimensional pre-multiplied spectra of the error in figure 20. It should be noted that all of these metrics are related to the ability of the methods to capture the unsteady behaviour of the fluctuations, rather than only the turbulence statistics.
In order to evaluate the computational cost of each method, a suitable parameter is the number of constructed transfer functions (which corresponds to around 20 s per transfer function on a typical workstation, without an optimized algorithm) and of performed convolutions (around 90 s each), which are the most expensive operations of the methods, accounting for more than 90 % of the total computational time. For the current approach, the number of convolutions and transfer functions which has to be calculated is the same. All these results are summarized in table 1.
Table 1. Summary of the error metrics and computational cost for the cases evaluated.
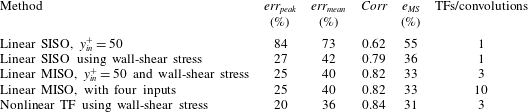
For this particular application, the nonlinear TF outperformed the MISO TF with two or four inputs, with the two MISO approaches presenting similar performances, indicating that the addition of more inputs in the log layer does not add information to the prediction of the near-wall peak. However, when one considers the accuracy variation along the wall-normal direction, it is observed that the MISO prediction exhibits better results, with the addition of measurements improving the predictions, such that the exact method of choice is dependent on the application and complexity of the experimental set-up to be used.
The linear TF using
![]() $y_{in}^{+}=50$
exhibits the worst behaviour, since it does not account for the fine-scale fluctuations, where most of the energy is contained in the near-wall region. Its spectrum is mainly due to larger fluctuations, indicating that such large structures behave linearly between the different wall heights, leaving a footprint on the near-wall structures. This trend is also observed in figure 20(a), where the error for this method is considerable at
$y_{in}^{+}=50$
exhibits the worst behaviour, since it does not account for the fine-scale fluctuations, where most of the energy is contained in the near-wall region. Its spectrum is mainly due to larger fluctuations, indicating that such large structures behave linearly between the different wall heights, leaving a footprint on the near-wall structures. This trend is also observed in figure 20(a), where the error for this method is considerable at
![]() $\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
, leading to a high error in the determination of the near-wall spectral peak.
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
, leading to a high error in the determination of the near-wall spectral peak.
The linear and nonlinear SISO and linear MISO predictions using wall-shear-stress velocity fluctuations above the wall, respectively, considerably improve the accuracy of the models and allow a reasonable determination of the inner peak, such that only the amplitude is slightly off in the predicted field. The main improvement comes from the use of wall-shear stress, which is highly correlated with the structures responsible for the near-wall dynamics.
The three methods evaluated in this work vary considerably in terms of their accuracy, with the linear SISO TF being significantly outperformed by the other approaches, particularly when an input in the log layer (
![]() $y_{in}^{+}=50$
or 100) is used to estimate the near-wall behaviour. There could be two explanations for such an observation: either the method to identify the transfer function is not efficiently capturing the linear mechanisms that occur, or there is not enough coherence between these two separated regions.
$y_{in}^{+}=50$
or 100) is used to estimate the near-wall behaviour. There could be two explanations for such an observation: either the method to identify the transfer function is not efficiently capturing the linear mechanisms that occur, or there is not enough coherence between these two separated regions.
The method proposed in § 5.1 could potentially exhibit errors with respect to the exact model either due to the presence of noise in the sensors that acquire the data for the system identification, or due to spectral leakage. The former is not present in this work, since the raw LES signals are taken directly for the construction of the model. As for the latter, it is avoided by means of using an adequately long time series, an assumption which was assessed by considering different lengths for the time series. Therefore, the implementation employed in this work can be regarded as the best linear approximation between the two positions separated in the wall-normal direction (Schoukens et al. Reference Schoukens, Rolain and Pintelon1997).
From
![]() $y_{in}^{+}=50$
or 100 one can only predict the footprint of the large scales on the near-wall region. This statement is supported by the two-dimensional coherence plots of figure 3, which show that only the long wavelengths are coherent, a behaviour further confirmed by the two-dimensional pre-multiplied spectra of the linear SISO prediction (figure 19), which contains only the large-scale structures. This also justifies for the large mismatch in the predicted variance. Furthermore, the attempts to use a nonlinear method with an input outside the buffer layer were unsuccessful. By considering the two-dimensional coherence plots (figure 3) it is evident that in order to capture the small-scale structures it is necessary to have access to data in the near-wall region (note that in this work we considered the wall-shear stress). An interesting method arises when data at the wall and
$y_{in}^{+}=50$
or 100 one can only predict the footprint of the large scales on the near-wall region. This statement is supported by the two-dimensional coherence plots of figure 3, which show that only the long wavelengths are coherent, a behaviour further confirmed by the two-dimensional pre-multiplied spectra of the linear SISO prediction (figure 19), which contains only the large-scale structures. This also justifies for the large mismatch in the predicted variance. Furthermore, the attempts to use a nonlinear method with an input outside the buffer layer were unsuccessful. By considering the two-dimensional coherence plots (figure 3) it is evident that in order to capture the small-scale structures it is necessary to have access to data in the near-wall region (note that in this work we considered the wall-shear stress). An interesting method arises when data at the wall and
![]() $y_{in}^{+}=50$
or 100 are used as prediction inputs, since these are complementary in terms of the coherence of the structures.
$y_{in}^{+}=50$
or 100 are used as prediction inputs, since these are complementary in terms of the coherence of the structures.
Other ways to capture this effect would be by directly adding the statistics of the remaining unpredicted field, as it is done with the universal signal in Marusic et al. (Reference Marusic, Mathis and Hutchins2010), or attempting a state estimator using the linearized Navier–Stokes system including an eddy-viscosity profile, as in Illingworth et al. (Reference Illingworth, Monty and Marusic2018), which is not straightforward for the linear SISO TF dealt with in this work. Comparable results to the two works cited above were obtained by means of the current approaches, where no extra modelling parameters are needed in order to perform the predictions. These comparisons will be discussed in further detail in § 7.
The computational cost of the MISO and nonlinear approaches evaluated here is about three times higher than that of the SISO linear case. However, we do not consider this difference to increase the cost such that it would be prohibitively expensive to implement these methods.
6 Off-design predictions
As outlined in the previous sections of this work, the on-line prediction of the designed transfer functions is made in two steps. The convolution kernels are firstly built using simultaneous time- and spanwise-resolved signals at the positions corresponding to inputs and output of the system, which are separated along the wall-normal direction. Once this system has been built, the prediction is made exclusively from measurements of the inputs.
This therefore raises questions accounting for the robustness of the methods for mild Reynolds-number variations, which would certainly be present in experimental applications. Furthermore, the fact that simultaneous measurements have to be performed as an initial step may lead to constraints in practical applications, where the correspondingly high Reynolds number would require a very fine resolution in the wall-normal direction, which may be difficult to obtain. Such constraints are shared by other methods available in the literature which require an initial set of data to build the model (also referred to as a training dataset in the context of machine learning methods).
One solution would therefore be to perform a large-eddy or direct numerical simulation of the geometry to be studied experimentally, and build the transfer functions a priori, which would only require the capability of measuring the inputs in the experiment (i.e. wall-shear stress and the fluctuations outside the buffer layer). Since high-fidelity simulations can typically only be performed at Reynolds numbers lower than those in certain experimental studies, it is of interest to design a model using a moderate Reynolds number, obtained from a high-fidelity simulation, and apply it to an experimental implementation at higher
![]() $Re$
. This possibility is explored in this section, where the transfer functions will be designed at
$Re$
. This possibility is explored in this section, where the transfer functions will be designed at
![]() $Re_{\unicode[STIX]{x1D703}}=880$
and tested at
$Re_{\unicode[STIX]{x1D703}}=880$
and tested at
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
, spanning approximately one order of magnitude in Reynolds number. Three cases will be considered here: linear SISO and MISO using wall shear and data outside the buffer layer, and the quadratic TF using wall-shear stress, which exhibits mild improvements in comparison to the linear case. The same input/output positions for the two Reynolds numbers will be considered in terms of the corresponding inner variables, which showed better performance than if the outer non-dimensionalization was utilized. Figure 21 shows the resulting correlations and variances for these three methods, for the original and off-design cases. For all the cases, the correlations in the off-design configurations are degraded, where the SISO implementation is the most affected. It should also be noted, however, that the prediction of the near-wall peak is not much affected, where compelling correlations are seen for the SISO using wall-shear stress and MISO methods. The prediction of the MISO transfer function is also less affected by the Reynolds-number variation, where it should be noted that for the case with four inputs, the off-design prediction remains with compelling correlations (above 60 %) throughout the evaluated range of wall-normal positions. The fact that the near-wall peak prediction from wall-shear data was practically unaffected supplies evidence that the near-wall region is directly correlated to the wall. The increase in
$Re_{\unicode[STIX]{x1D703}}=8200$
, spanning approximately one order of magnitude in Reynolds number. Three cases will be considered here: linear SISO and MISO using wall shear and data outside the buffer layer, and the quadratic TF using wall-shear stress, which exhibits mild improvements in comparison to the linear case. The same input/output positions for the two Reynolds numbers will be considered in terms of the corresponding inner variables, which showed better performance than if the outer non-dimensionalization was utilized. Figure 21 shows the resulting correlations and variances for these three methods, for the original and off-design cases. For all the cases, the correlations in the off-design configurations are degraded, where the SISO implementation is the most affected. It should also be noted, however, that the prediction of the near-wall peak is not much affected, where compelling correlations are seen for the SISO using wall-shear stress and MISO methods. The prediction of the MISO transfer function is also less affected by the Reynolds-number variation, where it should be noted that for the case with four inputs, the off-design prediction remains with compelling correlations (above 60 %) throughout the evaluated range of wall-normal positions. The fact that the near-wall peak prediction from wall-shear data was practically unaffected supplies evidence that the near-wall region is directly correlated to the wall. The increase in
![]() $Re$
has an effect on the large-scale modulation, modifying the footprint of the large-scale structures near the wall which in turn leads to the high degradation of the prediction of the near-wall peak when SISO transfer functions using data above the wall are used. We have therefore demonstrated the feasibility of designing SISO and MISO transfer functions at lower Reynolds numbers and implementing them at higher
$Re$
has an effect on the large-scale modulation, modifying the footprint of the large-scale structures near the wall which in turn leads to the high degradation of the prediction of the near-wall peak when SISO transfer functions using data above the wall are used. We have therefore demonstrated the feasibility of designing SISO and MISO transfer functions at lower Reynolds numbers and implementing them at higher
![]() $Re$
(one order of magnitude higher in this particular case), along with a considerable robustness of the methodology.
$Re$
(one order of magnitude higher in this particular case), along with a considerable robustness of the methodology.
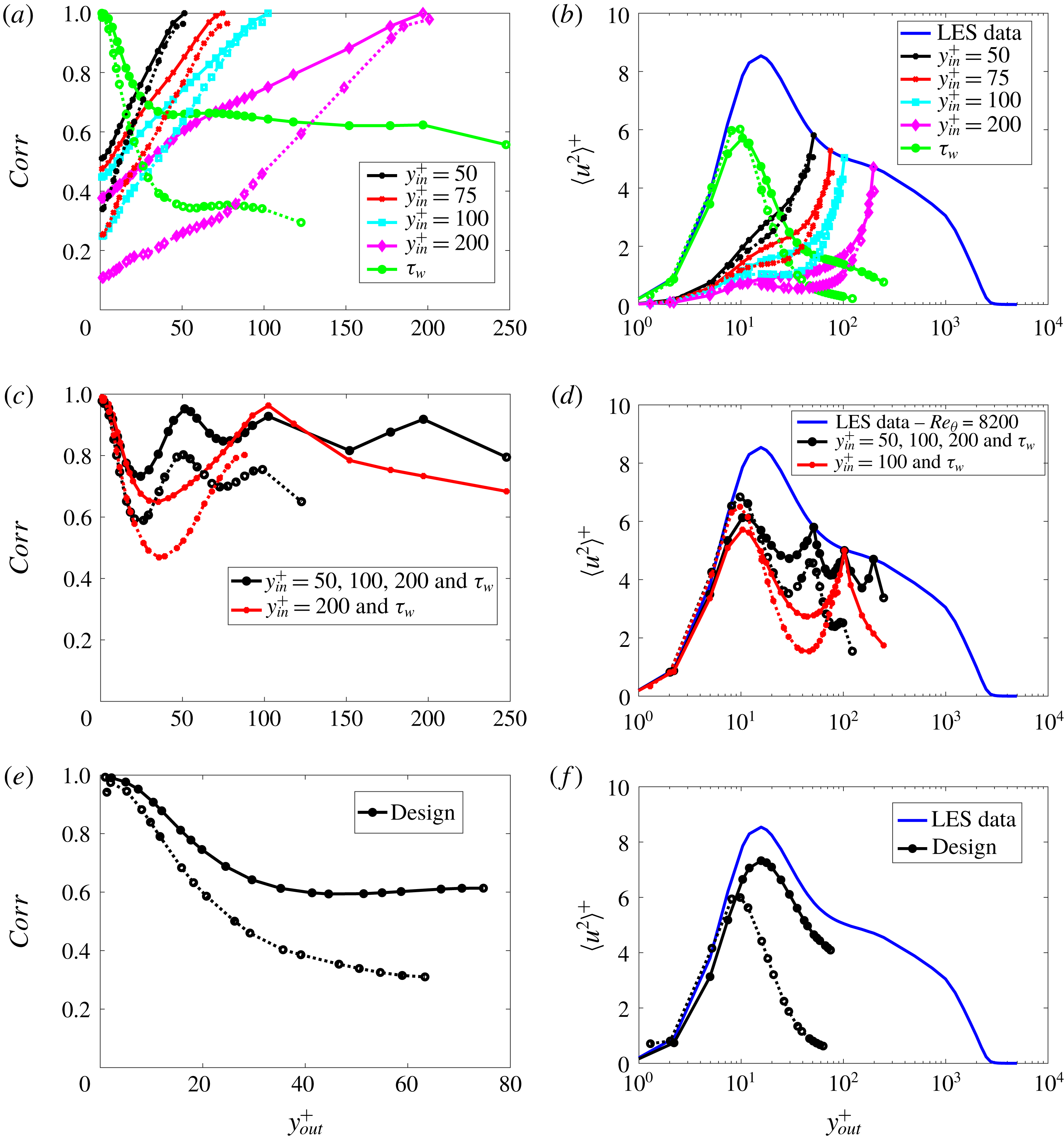
Figure 21. (a,c,e) Correlations between prediction and LES data and (b,d,f) comparison of the resulting variances using the SISO, MISO and nonlinear methods. Solid lines correspond to the same Reynolds number being used for design and test, whereas dotted lines are used for off-design cases, i.e. the model is built at
![]() $Re_{\unicode[STIX]{x1D703}}=880$
and tested at
$Re_{\unicode[STIX]{x1D703}}=880$
and tested at
![]() $Re_{\unicode[STIX]{x1D703}}=8200$
. (a) Correlations using linear SISO. (b) Variances using linear SISO. (c) Correlations using the linear MISO. (d) Variances using the linear MISO. (e) Correlations using quadratic SISO. (f) Variances using quadratic SISO.
$Re_{\unicode[STIX]{x1D703}}=8200$
. (a) Correlations using linear SISO. (b) Variances using linear SISO. (c) Correlations using the linear MISO. (d) Variances using the linear MISO. (e) Correlations using quadratic SISO. (f) Variances using quadratic SISO.
Although not shown for the sake of brevity, variations of up to 50 % in Reynolds number had no significant impact on the accuracy of the prediction. This feature is expected to be appealing for the application of the developed methods for experimental implementations, where uncertainties in the measured parameters are expected to be present.
7 Comparison with other methods
The methodologies developed in this work bear similarities with the recent studies by Baars et al. (Reference Baars, Hutchins and Marusic2016) and Illingworth et al. (Reference Illingworth, Monty and Marusic2018). The different focus of the first, which is on the characterization of the statistics, and application of the second, a channel at
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
, prevent quantitative comparisons of performance between these methods and the one proposed here. The objective of the current section is therefore to highlight differences in the approach, applicability, limitations and computational cost of the methods.
$Re_{\unicode[STIX]{x1D70F}}=1000$
, prevent quantitative comparisons of performance between these methods and the one proposed here. The objective of the current section is therefore to highlight differences in the approach, applicability, limitations and computational cost of the methods.
Illingworth et al. (Reference Illingworth, Monty and Marusic2018) considered a turbulent channel flow of
![]() $Re_{\unicode[STIX]{x1D70F}}=1000$
, obtained from DNS. Their approach is based on a Reynolds decomposition of the Navier–Stokes operator and gathering the nonlinear terms from the fluctuations into a forcing to an otherwise linear system. A Fourier transform is then applied to the homogeneous coordinates, corresponding to stream- and spanwise directions. The resulting inhomogeneous Orr–Sommerfeld squire (OSS) system is expressed in the form of an input/output state-space system, where the input corresponds to the forcing (nonlinear terms) and the output to the three velocity components. The idea is then to design a state observer, i.e. a linear operator that permits the estimation of the quantities based on a measurement of the three velocity components at a given height. This is made by means of an optimization problem, which enables the consideration of noise in the measurement sensors. The size of this problem is of the same order as the discretized Orr–Sommerfeld squire (OSS) operator, which could correspond to a square matrix of a few hundred lines. The computation of the model is made ‘off line’, without access to the simulated/experimental quantities. An eddy viscosity is added to the linear operator, and therefore a model is used for the determination of its behaviour along the wall-normal direction. Once the observer has been designed, the prediction is made by measuring the three velocity components at a given wall-normal plane and integrating the observer equations. The Fourier transform applied to the homogeneous directions implies that such measurements correspond to a whole plane in the span and streamwise directions, which is of course more difficult to accomplish experimentally than the proposal of the current work, in which we consider a spanwise line at a fixed streamwise position.
$Re_{\unicode[STIX]{x1D70F}}=1000$
, obtained from DNS. Their approach is based on a Reynolds decomposition of the Navier–Stokes operator and gathering the nonlinear terms from the fluctuations into a forcing to an otherwise linear system. A Fourier transform is then applied to the homogeneous coordinates, corresponding to stream- and spanwise directions. The resulting inhomogeneous Orr–Sommerfeld squire (OSS) system is expressed in the form of an input/output state-space system, where the input corresponds to the forcing (nonlinear terms) and the output to the three velocity components. The idea is then to design a state observer, i.e. a linear operator that permits the estimation of the quantities based on a measurement of the three velocity components at a given height. This is made by means of an optimization problem, which enables the consideration of noise in the measurement sensors. The size of this problem is of the same order as the discretized Orr–Sommerfeld squire (OSS) operator, which could correspond to a square matrix of a few hundred lines. The computation of the model is made ‘off line’, without access to the simulated/experimental quantities. An eddy viscosity is added to the linear operator, and therefore a model is used for the determination of its behaviour along the wall-normal direction. Once the observer has been designed, the prediction is made by measuring the three velocity components at a given wall-normal plane and integrating the observer equations. The Fourier transform applied to the homogeneous directions implies that such measurements correspond to a whole plane in the span and streamwise directions, which is of course more difficult to accomplish experimentally than the proposal of the current work, in which we consider a spanwise line at a fixed streamwise position.
Baars et al. (Reference Baars, Hutchins and Marusic2016) proposed a modification of the inner/outer interaction model by Marusic et al. (Reference Marusic, Mathis and Hutchins2010), where the superposition term, which was originally calculated by a linear operation over the input signal, is replaced by a linear stochastic estimator (LSE). Their flow case is a ZPG TBL of
![]() $Re_{\unicode[STIX]{x1D70F}}$
up to 19 000. The LSE is an entity calculated in the frequency domain and it requires measurements of the input and output quantities which are Fourier transformed to build a frequency-domain transfer function. The model is built using time measurements only, which is a configuration simpler to implement experimentally than the one proposed in this study. However, note that while we aim at predicting instantaneous quantities, the work of Baars et al. (Reference Baars, Hutchins and Marusic2016) is only focused on turbulence statistics. Once the LSE is available, a prediction is performed from Fourier-transformed measurements of the input. Since the predictions are obtained in the frequency domain and then inverse Fourier transformed, certain characteristics such as the causality of the prediction cannot be evaluated. The second part of the inner/outer interaction model is unchanged and its calculation involves an iterative procedure to find a demodulated ‘universal signal’ which ensures that the statistics of the resulting predicted signal are recovered. This also means that the full model, which exhibits very good agreement with experimental data, cannot be used for unsteady (time-domain) predictions, such as those necessary for control.
$Re_{\unicode[STIX]{x1D70F}}$
up to 19 000. The LSE is an entity calculated in the frequency domain and it requires measurements of the input and output quantities which are Fourier transformed to build a frequency-domain transfer function. The model is built using time measurements only, which is a configuration simpler to implement experimentally than the one proposed in this study. However, note that while we aim at predicting instantaneous quantities, the work of Baars et al. (Reference Baars, Hutchins and Marusic2016) is only focused on turbulence statistics. Once the LSE is available, a prediction is performed from Fourier-transformed measurements of the input. Since the predictions are obtained in the frequency domain and then inverse Fourier transformed, certain characteristics such as the causality of the prediction cannot be evaluated. The second part of the inner/outer interaction model is unchanged and its calculation involves an iterative procedure to find a demodulated ‘universal signal’ which ensures that the statistics of the resulting predicted signal are recovered. This also means that the full model, which exhibits very good agreement with experimental data, cannot be used for unsteady (time-domain) predictions, such as those necessary for control.
Finally, the method proposed here could be considered as an alternative to these two methods, depending on the desired application. Our results in terms of the predicted statistics are expected to be inferior to those of Baars et al. (Reference Baars, Hutchins and Marusic2016), with a moderately higher computational cost, since the method presented in that work avoids the use of a two-dimensional convolution. However, for time-domain predictions, the method outlined here is expected to outperform the one of Baars et al. (Reference Baars, Hutchins and Marusic2016), particularly when it is enhanced with multiple inputs which are complementary in terms of their coherent content with the output, a feature which, to the best of the authors’ knowledge, is not available in any other model in the literature for this particular application. The current method produces correlation coefficients on the same level as those of Illingworth et al. (Reference Illingworth, Monty and Marusic2018), with an expected lower computational cost and a simpler scheme to implement in an experimental application. The characteristics of the methods by Baars et al. (Reference Baars, Hutchins and Marusic2016) and Illingworth et al. (Reference Illingworth, Monty and Marusic2018), together with those of the method proposed in this study, are summarized in table 2.
8 Conclusions
Three different techniques were evaluated to predict the behaviour of the near-wall streamwise velocity fluctuations in ZPG turbulent boundary layers. The methods vary in terms of their inherent complexity and their potential difficulties in an experimental implementation.
Table 2. Summary of the characteristics of available models for the prediction of turbulence fluctuations in the time domain.
The linear, single-input–single-output (SISO) transfer function is the simplest and allows for predictions of the output signals from a single input measurement, here considered as space–time series of the streamwise velocity,
![]() $u(z,t)$
, at a given station
$u(z,t)$
, at a given station
![]() $x$
and wall-normal position
$x$
and wall-normal position
![]() $y$
. Reasonable performances were obtained for small separations along the wall-normal direction, leading to an eduction of the footprint of the large-scale fluctuations, a linear superposition of such structures on the near-wall region. Such footprint remained for wall-normal distances as high as
$y$
. Reasonable performances were obtained for small separations along the wall-normal direction, leading to an eduction of the footprint of the large-scale fluctuations, a linear superposition of such structures on the near-wall region. Such footprint remained for wall-normal distances as high as
![]() $y^{+}=250$
, as depicted in the results of figure 14. Note that although the amplitudes for such high separations were under-predicted, the phase of the predicted field still led to correlations of the order of 40 %. The implementation of this method in experimental applications would depend on the availability of two simultaneous measurements for constructing the TFs, one of them possibly corresponding to wall-shear stress. The availability of the SISO transfer function also allows for the derivation of linear control laws, as explored in other works by this group, for transitional flows (Sasaki et al.
Reference Sasaki, Morra, Fabbiane, Cavalieri, Hanifi and Henningson2018a
). Furthermore, as long as the wall-normal separation between input and output measurements is kept small, a reasonable prediction is obtained by this method.
$y^{+}=250$
, as depicted in the results of figure 14. Note that although the amplitudes for such high separations were under-predicted, the phase of the predicted field still led to correlations of the order of 40 %. The implementation of this method in experimental applications would depend on the availability of two simultaneous measurements for constructing the TFs, one of them possibly corresponding to wall-shear stress. The availability of the SISO transfer function also allows for the derivation of linear control laws, as explored in other works by this group, for transitional flows (Sasaki et al.
Reference Sasaki, Morra, Fabbiane, Cavalieri, Hanifi and Henningson2018a
). Furthermore, as long as the wall-normal separation between input and output measurements is kept small, a reasonable prediction is obtained by this method.
Addition of a quadratic term to the SISO prediction using wall-shear stress leads to a significant improvement of the prediction, particularly on what concerns the amplitude of the predicted signal. The mean square relative error corresponds to 31 % in the near-wall peak, with an error of 20 % in the determination of the near-wall spectral peak. The nonlinear prediction has the same experimental requirements as the linear one and would therefore be recommendable when a single wall-shear-stress measurement is available.
Finally, the multiple-input transfer function requires a more complex set-up, where several simultaneous measurements are required both for the construction of the model and the prediction. Nevertheless, improved performances were observed for this method, with the correlations between prediction and reference simulation data remaining above 70 %, from
![]() $y_{out}^{+}=180$
until the wall, when four input measurements were considered. Since this method corresponds to a linear approach, the use of standard linear control techniques may be carried out directly within this framework (Bendat & Piersol Reference Bendat and Piersol2011). This is the most interesting approach for data reconstruction from a limited set of measurements, since it produces velocity fields in compelling agreement with the reference data.
$y_{out}^{+}=180$
until the wall, when four input measurements were considered. Since this method corresponds to a linear approach, the use of standard linear control techniques may be carried out directly within this framework (Bendat & Piersol Reference Bendat and Piersol2011). This is the most interesting approach for data reconstruction from a limited set of measurements, since it produces velocity fields in compelling agreement with the reference data.
The differences between the resulting accuracy of the methods were understood in terms of the coherence between the considered wall-normal positions and it was shown that the footprint of the large scales in the outer layer can be connected to a linear mechanism, educed by the linear SISO transfer function. This footprint is considered as a linear superposition in the model of Marusic et al. (Reference Marusic, Mathis and Hutchins2010) and is here directly extracted from the data via the linear transfer function approach.
In summary, when considering the reference output position at
![]() $y_{out}^{+}=15$
, it is observed that the linear SISO with a measurement outside the buffer layer can only capture the linear footprint of the large scales, which leads to considerable errors in the spectral content and variances of the prediction, as only approximately 40 % of the energy in this position can be reproduced by the linear method. The use of nonlinear terms was ineffective for this case, indicating mostly a linear correlation between the large scales and the near-wall region. By measuring wall-shear stress, the prediction is considerably improved, leading to errors of 36 % and 31 %, depending on whether the linear or nonlinear methodology is performed. The use of a quadratic term here improved the predictions, a trend which had been previously observed (Naguib et al.
Reference Naguib, Wark and Juckenhöfel2001) and which is related to turbulent–turbulent interactions of the fluctuations. As for the MISO prediction, even though it does not outperform the nonlinear analysis for the output at
$y_{out}^{+}=15$
, it is observed that the linear SISO with a measurement outside the buffer layer can only capture the linear footprint of the large scales, which leads to considerable errors in the spectral content and variances of the prediction, as only approximately 40 % of the energy in this position can be reproduced by the linear method. The use of nonlinear terms was ineffective for this case, indicating mostly a linear correlation between the large scales and the near-wall region. By measuring wall-shear stress, the prediction is considerably improved, leading to errors of 36 % and 31 %, depending on whether the linear or nonlinear methodology is performed. The use of a quadratic term here improved the predictions, a trend which had been previously observed (Naguib et al.
Reference Naguib, Wark and Juckenhöfel2001) and which is related to turbulent–turbulent interactions of the fluctuations. As for the MISO prediction, even though it does not outperform the nonlinear analysis for the output at
![]() $y_{out}^{+}=15$
, given that it deals with inputs of complementary coherence, it permits to obtain low error values throughout the range of wall-normal positions, depending on the number of inputs considered, presenting therefore overall better performances than the SISO methods.
$y_{out}^{+}=15$
, given that it deals with inputs of complementary coherence, it permits to obtain low error values throughout the range of wall-normal positions, depending on the number of inputs considered, presenting therefore overall better performances than the SISO methods.
Although not shown here, the same analysis with the different methods evaluated here was also performed for other input/output quantities. Very similar trends and levels of accuracy were observed when the same quantity was used as input and output (i.e. wall-normal and spanwise velocity or pressure fluctuations both as the measured and estimated quantities, for example).
The present work also shows a significant robustness of the various methods concerning Reynolds-number variations between the data used to construct the transfer functions and to perform the flow predictions. It is proposed that the present methodology could be used in experimental studies at higher Reynolds numbers, where it is very difficult to accurately measure close to the wall. A test spanning a one order of magnitude variation in Reynolds number (between the data used to build the model and for the predictions) led to very satisfactory results, providing evidence of the feasibility of this approach.
Comparison between the method outlined in this article with the recent work of Baars et al. (Reference Baars, Hutchins and Marusic2016) demonstrates an expected higher accuracy in the time-domain predictions along with the possibility of using our method for in the design of control laws; furthermore, a simpler experimental set-up would be required compared to that of the method by Illingworth et al. (Reference Illingworth, Monty and Marusic2018) along with a lower computational demand. To summarize, the strategy proposed here demonstrates a high flexibility in terms of input/output measurements which could be advantageous for implementations in flow control and at high
![]() $Re$
, where the exact choice of method (SISO/MISO, linear/nonlinear) would depend on the available experimental setting, the desired accuracy and the particular application.
$Re$
, where the exact choice of method (SISO/MISO, linear/nonlinear) would depend on the available experimental setting, the desired accuracy and the particular application.
Acknowledgements
Part of this work has been developed during an exchange programme to KTH, when the first author appreciated a scholarship from Capes, project number 88881.132008/2016-01. K.S. has obtained a scholarship from FAPESP, grant no. 2016/25187-4. A.V.G.C. was supported by a CNPq grant 310523/2017-6. The authors would also like to acknowledge the funding from PreLaFloDes, Swedemo and CISB (Swedish-Brazilian Research and Innovation Centre). R.V. and P.S. acknowledge the funding provided by the Swedish Research Council (VR) and from the Knut and Alice Wallenberg Foundation. This research is also supported by the ERC grant no. ‘2015-AdG-694452, TRANSEP’ to D.S.H.
Appendix A. Calculation of the transfer functions
This section outlines the procedure to calculate the power spectral densities used in the calculation of the
![]() $(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
transfer functions as per (4.3). The case of the auto power spectral density will be considered, however the method is easily adapted for the cross power spectral density case.
$(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
transfer functions as per (4.3). The case of the auto power spectral density will be considered, however the method is easily adapted for the cross power spectral density case.
Consider the signal
![]() $I(z,t)$
, measured along the spanwise direction and time, where
$I(z,t)$
, measured along the spanwise direction and time, where
![]() $z$
is a periodic direction. The auto spectral density of such signal is then defined as,
$z$
is a periodic direction. The auto spectral density of such signal is then defined as,
where the double hat indicates a double Fourier transform from
![]() $z$
to
$z$
to
![]() $\unicode[STIX]{x1D6FD}$
and from
$\unicode[STIX]{x1D6FD}$
and from
![]() $t$
to
$t$
to
![]() $\unicode[STIX]{x1D714}$
. The first transform is taken along the
$\unicode[STIX]{x1D714}$
. The first transform is taken along the
![]() $z$
direction,
$z$
direction,
Upon discretization in
![]() $z$
, the continuous Fourier transform becomes a discrete Fourier transform (DFT). Since this direction is periodic, the DFT may be regarded directly as the discretization of the coefficients of the corresponding Fourier series.
$z$
, the continuous Fourier transform becomes a discrete Fourier transform (DFT). Since this direction is periodic, the DFT may be regarded directly as the discretization of the coefficients of the corresponding Fourier series.
Consider now the discretization in time, with a total number of
![]() $N$
snapshots, such that the signal may be regarded as:
$N$
snapshots, such that the signal may be regarded as:
where
![]() $\hat{I} (\unicode[STIX]{x1D6FD})$
is
$\hat{I} (\unicode[STIX]{x1D6FD})$
is
![]() $N_{\unicode[STIX]{x1D6FD}}\times N$
,
$N_{\unicode[STIX]{x1D6FD}}\times N$
,
![]() $N_{\unicode[STIX]{x1D6FD}}$
corresponding to the total number of transverse wavenumbers considered. It is a known result (Bendat & Piersol Reference Bendat and Piersol2011) that the direct application of the DFT on the lines of
$N_{\unicode[STIX]{x1D6FD}}$
corresponding to the total number of transverse wavenumbers considered. It is a known result (Bendat & Piersol Reference Bendat and Piersol2011) that the direct application of the DFT on the lines of
![]() $\hat{I} (t,\unicode[STIX]{x1D6FD})$
should not be performed, as the result will not converge with the increasing number of snapshots
$\hat{I} (t,\unicode[STIX]{x1D6FD})$
should not be performed, as the result will not converge with the increasing number of snapshots
![]() $N$
. The error in the estimate of each frequency could be as high as the calculated magnitude of the corresponding auto spectrum. In order to obtain converged estimates it is necessary to appropriately average the spectra over multiple ensembles of the flow, which may be accomplished by Welch’s method (Welch Reference Welch1967). Start by partitioning the full signal into
$N$
. The error in the estimate of each frequency could be as high as the calculated magnitude of the corresponding auto spectrum. In order to obtain converged estimates it is necessary to appropriately average the spectra over multiple ensembles of the flow, which may be accomplished by Welch’s method (Welch Reference Welch1967). Start by partitioning the full signal into
![]() $N_{b}$
blocks with
$N_{b}$
blocks with
![]() $N_{f}$
elements, such that the nth block is given as:
$N_{f}$
elements, such that the nth block is given as:
with each block referred to a realization of the flow. The blocks may also present an overlap region with the adjacent elements, which allows for an increased number of blocks for the same length of the original signal, permitting a faster convergence of the algorithm. The
![]() $k$
th entry in the
$k$
th entry in the
![]() $n$
th block is then given as
$n$
th block is then given as
![]() $\hat{I} _{k}^{(n)}(\unicode[STIX]{x1D6FD})=\hat{I} _{k+(n-1)(N_{f}-N_{o})}(\unicode[STIX]{x1D6FD})$
, where
$\hat{I} _{k}^{(n)}(\unicode[STIX]{x1D6FD})=\hat{I} _{k+(n-1)(N_{f}-N_{o})}(\unicode[STIX]{x1D6FD})$
, where
![]() $N_{o}$
is the number of overlapping snapshots. The DFT is then calculated at each block,
$N_{o}$
is the number of overlapping snapshots. The DFT is then calculated at each block,
such that:
for
![]() $k=1,\ldots ,N_{f}$
and
$k=1,\ldots ,N_{f}$
and
![]() $n=1,\ldots ,N_{b}$
. This represents the DFT of the block, adding the weights
$n=1,\ldots ,N_{b}$
. This represents the DFT of the block, adding the weights
![]() $w_{j}$
to determine the application of a window function which is used to reduce spectral leakage due to each block being non-periodic. The normalization factor
$w_{j}$
to determine the application of a window function which is used to reduce spectral leakage due to each block being non-periodic. The normalization factor
![]() $1/N_{f}$
ensures that the DFT is unitary for a square window. Therefore,
$1/N_{f}$
ensures that the DFT is unitary for a square window. Therefore,
![]() $\hat{\hat{I} }_{k}(\unicode[STIX]{x1D6FD})$
is the DFT at a frequency
$\hat{\hat{I} }_{k}(\unicode[STIX]{x1D6FD})$
is the DFT at a frequency
![]() $\unicode[STIX]{x1D714}_{k}$
, for each block, and
$\unicode[STIX]{x1D714}_{k}$
, for each block, and
or
To simplify the notation, the subscript
![]() $k$
is dropped from the frequency components in the remaining of this section and in the main body of the paper.
$k$
is dropped from the frequency components in the remaining of this section and in the main body of the paper.
Finally,
![]() $S_{II}$
at a pair
$S_{II}$
at a pair
![]() $(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
is calculated by averaging the blocks,
$(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$
is calculated by averaging the blocks,
 $$\begin{eqnarray}S_{II}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})=\frac{\unicode[STIX]{x0394}t}{\displaystyle \mathop{\sum }_{j=1}^{N_{f}}w_{j}^{2}N_{b}}\mathop{\sum }_{n=1}^{N_{b}}\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})[\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})]^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}S_{II}(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})=\frac{\unicode[STIX]{x0394}t}{\displaystyle \mathop{\sum }_{j=1}^{N_{f}}w_{j}^{2}N_{b}}\mathop{\sum }_{n=1}^{N_{b}}\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})[\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})]^{\ast },\end{eqnarray}$$
which converges as the number of snapshots and blocks is increased together. The final value obtained from this average is referred to as the expected value of the quantity
![]() $\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})[\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})]^{\ast }$
and the process to obtain it is referred to as an ensemble average.
$\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})[\hat{\hat{I} }(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})]^{\ast }$
and the process to obtain it is referred to as an ensemble average.
Appendix B. Decorrelation via spectral conditioning
The spectral conditioning technique consists in removing all the linear influence that exists between the inputs, hence decorrelating them (Bendat & Piersol Reference Bendat and Piersol2011). The technique is performed iteratively, the first input remains unchanged and all the others have to be computed. In order to spectral conditionally remove the influence of input 1 over input 2, for example, the following operation is performed in the frequency domain
which, in the time domain is equivalent to
where
![]() $\otimes$
indicates a double convolution and the subscript
$\otimes$
indicates a double convolution and the subscript
![]() $2-1$
indicates that input 1 is linearly decorrelated from input 2, via the transfer function
$2-1$
indicates that input 1 is linearly decorrelated from input 2, via the transfer function
![]() $g_{I_{1}I_{2}}$
, which relates the two inputs. For the sake of brevity, the following operations will be shown only in the time domain, where the definition of the linear transfer function is implicit. The third input has to be decorrelated from
$g_{I_{1}I_{2}}$
, which relates the two inputs. For the sake of brevity, the following operations will be shown only in the time domain, where the definition of the linear transfer function is implicit. The third input has to be decorrelated from
![]() $I_{1}(t,z)$
and
$I_{1}(t,z)$
and
![]() $I_{2-1}(t,z)$
, such that
$I_{2-1}(t,z)$
, such that
where the subscript
![]() $3-2!$
indicates the decorrelation of input 3 from inputs 2 and 1. For the
$3-2!$
indicates the decorrelation of input 3 from inputs 2 and 1. For the
![]() $N$
th input, the decorrelation results in
$N$
th input, the decorrelation results in