Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-18T18:15:30.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow

Published online by Cambridge University Press:  30 July 2013

A. Rao ,
J. S. Leontini ,
M. C. Thompson  and
K. Hourigan
A. Rao
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
J. S. Leontini*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
M. C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
K. Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia Division of Biological Engineering, Monash University, Melbourne, Victoria 3800, Australia
*
†Email address for correspondence: justin.leontini@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow around an isolated cylinder spinning at high rotation rates in free stream is investigated. The existence of two steady two-dimensional states is confirmed, as is the existence of a secondary mode of vortex shedding. The stability of the two steady states to three-dimensional perturbations is established using linear stability analysis. At lower rotation rates on the first steady state, two three-dimensional modes are confirmed, and their structure and curves of marginal stability as a function of rotation rate and Reynolds number are determined. 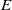One mode (named mode $E$) appears consistent with a hyperbolic instability in the wake, while the second (named mode 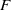$F$) appears to be a centrifugal instability of the flow very close to the cylinder surface. At higher rotation rates on the second steady state, a single three-dimensional mode due to centrifugal instability (named mode 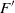${F}^{\prime } $) is found. This mode becomes increasingly difficult to excite as the rotation rate is increased.

JFM classification

Instability: Parametric instability Vortex Flows: Vortex Flows Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 379 - 391
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Drazin, P. G. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.Google Scholar
El Akoury, R., Braza, M., Perrin, R., Harran, G. & Hoarau, Y. 2008 The three-dimensional transition in the flow around a rotating cylinder. J. Fluid Mech. 607, 1–11.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/hp Methods for Computational Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
Kumar, S., Cantu, C. & Gonzalez, B. 2011 Flow past a rotating cylinder at low and high rotation rates. Trans. ASME: J. Fluids Engng 133 (4), 041201.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.Google Scholar
Lo Jacono, D., Leontini, J. S., Thompson, M. C. & Sheridan, J. 2010 Modification of three-dimensional transition in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 643, 349–362.Google Scholar
Meena, J., Sidharth, G. S., Khan, M. H. & Mittal, S. 2011 Three-dimensional instabilities in flow past a spinning and translating cylinder. In IUTAM Symposium on Bluff Body Flows, pp. 59–62. Indian Institute of Technology Kanpur.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Padrino, J. C. & Joseph, D. D. 2006 Numerical study of the steady-state uniform flow past a rotating cylinder. J. Fluid Mech. 557, 191–223.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.Google Scholar
Prandtl, L. 1926 Application of the ‘Magnus Effect’ to the Wind Propulsion of Ships. National Advisory Committee for Aeronautics.Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013 Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.CrossRefGoogle Scholar
Rayleigh, J. W. Strutt, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. Ser. A 93, 148–154.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.Google Scholar
Stojković, D., Breuer, M. & Durst, F. 2002 Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 1 (9), 3160–3178.Google Scholar
Stojković, D., Schön, P., Breuer, M. & Durst, F. 2003 On the new vortex shedding mode past a rotating circular cylinder. Phys. Fluids 15 (5), 1257–1260.Google Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. Ser. A 223, 289–343.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 1356–1369.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12 (2), 190–196.Google Scholar