Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T01:41:25.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic modelling of a noise-driven global instability in a turbulent swirling jet

Published online by Cambridge University Press:  06 April 2021

Moritz Sieber Open the ORCID record for Moritz Sieber [Opens in a new window] ,
C. Oliver Paschereit  and
Kilian Oberleithner Open the ORCID record for Kilian Oberleithner [Opens in a new window]
Moritz Sieber*
Affiliation:
Chair of Fluid Dynamics, Institut für Strömungsmechanik und Technische Akustik, Technische Universität Berlin, 10623Berlin, Germany Laboratory for Flow Instabilities and Dynamics, Institut für Strömungsmechanik und Technische Akustik, Technische Universität Berlin, 10623Berlin, Germany
C. Oliver Paschereit
Affiliation:
Chair of Fluid Dynamics, Institut für Strömungsmechanik und Technische Akustik, Technische Universität Berlin, 10623Berlin, Germany
Kilian Oberleithner
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Institut für Strömungsmechanik und Technische Akustik, Technische Universität Berlin, 10623Berlin, Germany
*
†Email address for correspondence: moritz.sieber@fd.tu-berlin.de
Get access Rights & Permissions [Opens in a new window]

Abstract

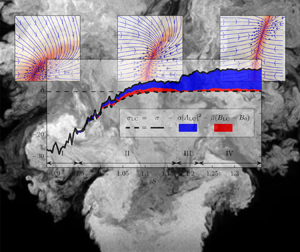
A method is developed to estimate the properties of a global hydrodynamic instability in turbulent flows from measurement data of the limit-cycle oscillations. For this purpose, the flow dynamics is separated into deterministic contributions representing the global mode and a stochastic contribution representing the intrinsic turbulent forcing. Stochastic models are developed that account for the interaction between the two and allow the determination of the dynamic properties of the flow from stationary data. The deterministic contributions are modelled by an amplitude equation, which describes the oscillatory dynamics of the instability, and in a second approach by a mean-field model, which additionally captures the interaction between the instability and the mean-flow corrections. The stochastic contributions are considered as coloured noise forcing, representing the spectral characteristics of the stochastic turbulent perturbations. The methodology is applied to a turbulent swirling jet with a dominant global mode. Particle image velocimetry measurements are conducted to ensure that the mode is the most dominant coherent structure, and further pressure measurements provide long time series for the model calibration. The supercritical Hopf bifurcation is identified from the linear growth rate of the global mode, and the excellent agreement between measured and estimated statistics suggest that the model captures the relevant dynamics. This work demonstrates that the sole observation of limit-cycle oscillations is not sufficient to determine the stability of turbulent flows, since the stochastic perturbations obscure the actual bifurcation point. However, the proposed separation of deterministic and stochastic contributions in the dynamical model allows the identification of the flow state from stationary measurements.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Turbulent Flows: Turbulence modelling Vortex Flows: Vortex breakdown
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 916 , 10 June 2021 , A7
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.CrossRefGoogle Scholar
Bonciolini, G., Boujo, E. & Noiray, N. 2017 Output-only parameter identification of a colored-noise-driven Van-der-Pol oscillator: thermoacoustic instabilities as an example. Phys. Rev. E 95 (6), 062217.CrossRefGoogle ScholarPubMed
Boujo, E., Bourquard, C., Xiong, Y. & Noiray, N. 2020 Processing time-series of randomly forced self-oscillators: the example of beer bottle whistling. J. Sound Vib. 464, 114981.CrossRefGoogle Scholar
Boujo, E. & Cadot, O. 2019 Stochastic modeling of a freely rotating disk facing a uniform flow. J. Fluids Struct. 86, 34–43.CrossRefGoogle Scholar
Boujo, E. & Noiray, N. 2017 Robust identification of harmonic oscillator parameters using the adjoint Fokker–Planck equation. Proc. R. Soc. A 473 (2200), 20160894.CrossRefGoogle ScholarPubMed
Brackston, R.D., García de la Cruz, J.M., Wynn, A., Rigas, G. & Morrison, J.F. 2016 Stochastic modelling and feedback control of bistability in a turbulent bluff body wake. J. Fluid Mech. 802, 726–749.CrossRefGoogle Scholar
Brunton, S.L., Proctor, J.L. & Kutz, J.N. 2016 Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113 (15), 3932–3937.CrossRefGoogle ScholarPubMed
Carini, M., Airiau, C., Debien, A., Léon, O. & Pralits, J.O. 2017 Global stability and control of the confined turbulent flow past a thick flat plate. Phys. Fluids 29 (2), 024102.CrossRefGoogle Scholar
Chigier, N.A. & Chervinsky, A. 1967 Experimental investigation of swirling vortex motion in jets. Trans. ASME: J. Appl. Mech. 34 (2), 443–451.CrossRefGoogle Scholar
Coller, B.D., Holmes, P. & Lumley, J.L. 1994 Control of noisy heteroclinic cycles. Physica D 72 (1–2), 135–160.CrossRefGoogle Scholar
Friedrich, R. & Peinke, J. 1997 Description of a turbulent cascade by a Fokker–Planck equation. Phys. Rev. Lett. 78 (5), 863–866.CrossRefGoogle Scholar
Friedrich, R., Peinke, J., Sahimi, M. & Reza Rahimi Tabar, M. 2011 Approaching complexity by stochastic methods: from biological systems to turbulence. Phys. Rep. 506 (5), 87–162.CrossRefGoogle Scholar
Friedrich, R., Siegert, S., Peinke, J., St. Lück, S.M., Lindemann, M., Raethjen, J., Deuschl, G. & Pfister, G. 2000 Extracting model equations from experimental data. Phys. Lett. A 271 (3), 217–222.CrossRefGoogle Scholar
Gallaire, F. & Chomaz, J.-M. 2003 Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.CrossRefGoogle Scholar
Gallaire, F., Ruith, M.R., Meiburg, E., Chomaz, J.-M. & Huerre, P. 2006 Spiral vortex breakdown as a global mode. J. Fluid Mech. 549, 71–80.CrossRefGoogle Scholar
Gang, H., Ditzinger, T., Ning, C.-Z. & Haken, H. 1993 Stochastic resonance without external periodic force. Phys. Rev. Lett. 71 (6), 807–810.CrossRefGoogle ScholarPubMed
Hänggi, P. & Jung, P. 1994 Colored noise in dynamical systems. In Advances in Chemical Physics (ed. I. Prigogine & S.A. Rice), vol. 18, pp. 239–326. John Wiley & Sons.CrossRefGoogle Scholar
Holmes, P., Lumley, J.L., Berkooz, G. & Rowley, C.W. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd edn. Cambridge Monographs on Mechanics. Cambridge University Press.CrossRefGoogle Scholar
Huang, H.T., Fiedler, H.E. & Wang, J.J. 1993 Limitation and improvement of PIV. Part 2. Particle image distortion, a novel technique. Exp. Fluids 15 (4–5), 263–273.CrossRefGoogle Scholar
Kabiraj, L., Steinert, R., Saurabh, A. & Paschereit, C.O. 2015 Coherence resonance in a thermoacoustic system. Phys. Rev. E 92 (4), 042909.CrossRefGoogle Scholar
Kaiser, E., Noack, B.R., Cordier, L., Spohn, A., Segond, M., Abel, M., Daviller, G., Östh, J., Krajnović, S. & Niven, R.K. 2014 Cluster-based reduced-order modelling of a mixing layer. J. Fluid Mech. 754, 365–414.CrossRefGoogle Scholar
Kleinhans, D. & Friedrich, R. 2007 Maximum likelihood estimation of drift and diffusion functions. Phys. Lett. A 368 (3–4), 194–198.CrossRefGoogle Scholar
Landau, L.D. 1944 On the problem of turbulence. C. R. Acad. Sci. URSS 44, 311–314.Google Scholar
Landau, L.D. & Lifshitz, E.M. 1987 Fluid Mechanics, 2nd edn. Course of Theoretical Physics, vol. 6. Pergamon.Google Scholar
Lasagna, D., Orazi, M. & Iuso, G. 2013 Multi-time delay, multi-point linear stochastic estimation of a cavity shear layer velocity from wall-pressure measurements. Phys. Fluids 25 (1), 017101.CrossRefGoogle Scholar
Lee, M., Kim, K.T., Gupta, V. & Li, L.K.B. 2020 System identification and early warning detection of thermoacoustic oscillations in a turbulent combustor using its noise-induced dynamics. Proc. Combust. Inst. (in press).CrossRefGoogle Scholar
Lee, M., Zhu, Y., Li, L.K.B. & Gupta, V. 2019 System identification of a low-density jet via its noise-induced dynamics. J. Fluid Mech. 862, 200–215.CrossRefGoogle Scholar
Lehle, B. & Peinke, J. 2018 Analyzing a stochastic process driven by Ornstein–Uhlenbeck noise. Phys. Rev. E 97 (1-1), 012113.CrossRefGoogle ScholarPubMed
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.CrossRefGoogle Scholar
Ljung, L. 2012 System Identification: Theory for the User, 2nd edn. Prentice Hall Information and System Sciences Series. Prentice Hall PTR.Google Scholar
Luchtenburg, D.M., Günther, B., Noack, B.R., King, R. & Tadmor, G. 2009 A generalized mean-field model of the natural and high-frequency actuated flow around a high-lift configuration. J. Fluid Mech. 623, 283–316.CrossRefGoogle Scholar
Lui, H.F.S. & Wolf, W.R. 2019 Construction of reduced-order models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 872, 963–994.CrossRefGoogle Scholar
Mantič-Lugo, V., Arratia, C. & Gallaire, F. 2015 A self-consistent model for the saturation dynamics of the vortex shedding around the mean flow in the unstable cylinder wake. Phys. Fluids 27 (7), 074103.CrossRefGoogle Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012 a A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.CrossRefGoogle Scholar
Meliga, P., Pujals, G. & Serre, É. 2012 b Sensitivity of 2-D turbulent flow past a d-shaped cylinder using global stability. Phys. Fluids 24 (6), 061701.CrossRefGoogle Scholar
Müller, J.S., Lückoff, F., Paredes, P., Theofilis, V. & Oberleithner, K. 2020 Receptivity of the turbulent precessing vortex core: synchronization experiments and global adjoint linear stability analysis. J. Fluid Mech. 888, A3.CrossRefGoogle Scholar
Noack, B.R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
Noack, B.R., Stankiewicz, W., Morzyński, M. & Schmid, P.J. 2016 Recursive dynamic mode decomposition of transient and post-transient wake flows. J. Fluid Mech. 809, 843–872.CrossRefGoogle Scholar
Noiray, N. 2017 Linear growth rate estimation from dynamics and statistics of acoustic signal envelope in turbulent combustors. Trans. ASME: J. Engng Gas Turbines Power 139 (4), 041503.Google Scholar
Noiray, N. & Schuermans, B. 2013 Deterministic quantities characterizing noise driven Hopf bifurcations in gas turbine combustors. Intl J. Non-Linear Mech. 50, 152–163.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C.O., Seele, R. & Wygnanski, I. 2012 Formation of turbulent vortex breakdown: intermittency, criticality, and global instability. AIAA J. 50 (7), 1437–1452.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C.O. & Wygnanski, I. 2014 On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.CrossRefGoogle Scholar
Oberleithner, K., Sieber, M., Nayeri, C.N., Paschereit, C.O., Petz, C., Hege, H.-C., Noack, B.R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.CrossRefGoogle Scholar
Qadri, U.A., Mistry, D. & Juniper, M.P. 2013 Structural sensitivity of spiral vortex breakdown. J. Fluid Mech. 720, 558–581.CrossRefGoogle Scholar
Reinke, N., Fuchs, A., Nickelsen, D. & Peinke, J. 2018 On universal features of the turbulent cascade in terms of non-equilibrium thermodynamics. J. Fluid Mech. 848, 117–153.CrossRefGoogle Scholar
Ribeiro, J.H.M. & Wolf, W.R. 2017 Identification of coherent structures in the flow past a NACA0012 airfoil via proper orthogonal decomposition. Phys. Fluids 29 (8), 085104.CrossRefGoogle Scholar
Rigas, G., Morgans, A.S., Brackston, R.D. & Morrison, J.F. 2015 Diffusive dynamics and stochastic models of turbulent axisymmetric wakes. J. Fluid Mech. 778, R2.CrossRefGoogle Scholar
Roberts, J.B. & Spanos, P.D. 1986 Stochastic averaging: an approximate method of solving random vibration problems. Intl J. Non-Linear Mech. 21 (2), 111–134.CrossRefGoogle Scholar
Ruith, M.R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
Rukes, L., Paschereit, C.O. & Oberleithner, K. 2016 An assessment of turbulence models for linear hydrodynamic stability analysis of strongly swirling jets. Eur. J. Mech. B/Fluids 59, 205–218.CrossRefGoogle Scholar
Rukes, L., Sieber, M., Paschereit, C.O. & Oberleithner, K. 2015 Effect of initial vortex core size on the coherent structures in the swirling jet near field. Exp. Fluids 56 (10), 183.CrossRefGoogle Scholar
Saurabh, A., Kabiraj, L., Steinert, R. & Oliver Paschereit, C. 2017 Noise-induced dynamics in the subthreshold region in thermoacoustic systems. Trans. ASME: J. Engng Gas Turbines Power 139 (3), 031508.Google Scholar
Sieber, M., Paschereit, C.O. & Oberleithner, K. 2016 a Advanced identification of coherent structures in swirl-stabilized combustors. Trans. ASME: J. Engng Gas Turbines Power 139 (2), 021503.Google Scholar
Sieber, M., Paschereit, C.O. & Oberleithner, K. 2016 b Spectral proper orthogonal decomposition. J. Fluid Mech. 792, 798–828.CrossRefGoogle Scholar
Sieber, M., Paschereit, C.O. & Oberleithner, K. 2017 On the nature of spectral proper orthogonal decomposition and related modal decompositions. arXiv:1712.08054.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part 1. Coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Soria, J. 1996 An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Expl Therm. Fluid Sci. 12 (2), 221–233.CrossRefGoogle Scholar
Stöhr, M., Oberleithner, K., Sieber, M., Yin, Z. & Meier, W. 2018 Experimental study of transient mechanisms of bi-stable flame shape transitions in a swirl combustor. Trans. ASME: J. Engng Gas Turbines Power 140 (1), 0742-4795.Google Scholar
Stone, E. & Holmes, P. 1989 Noise induced intermittency in a model of a turbulent boundary layer. Physica D 37 (1–3), 20–32.CrossRefGoogle Scholar
Stuart, J.T. 1958 On the non-linear mechanics of hydrodynamic stability. J. Fluid Mech. 4 (1), 1–21.CrossRefGoogle Scholar
Syred, N. & Beér, J.M. 1974 Combustion in swirling flows: a review. Combust. Flame 23 (2), 143–201.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M.P. 2016 Coherent structures in a swirl injector at $Re = 4800$ by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Terhaar, S., Reichel, T.G., Schrödinger, C., Rukes, L., Paschereit, C.O. & Oberleithner, K. 2014 Vortex breakdown types and global modes in swirling combustor flows with axial injection. J. Propul. Power 31 (1), 219–229.CrossRefGoogle Scholar
Tocino, A. & Ardanuy, R. 2002 Runge–Kutta methods for numerical solution of stochastic differential equations. J. Comput. Appl. Maths 138 (2), 219–241.CrossRefGoogle Scholar
Towne, A., Schmidt, O.T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Turton, S.E., Tuckerman, L.S. & Barkley, D. 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E 91 (4), 043009.CrossRefGoogle ScholarPubMed
Vanierschot, M. & Ogus, G. 2019 Experimental investigation of the precessing vortex core in annular swirling jet flows in the transitional regime. Expl Therm. Fluid Sci. 106, 148–158.CrossRefGoogle Scholar
Villermaux, E. & Hopfinger, E.J. 1994 Periodically arranged co-flowing jets. J. Fluid Mech. 263, 63–92.CrossRefGoogle Scholar
Viola, F., Iungo, G.V., Camarri, S., Porté-Agel, F. & Gallaire, F. 2014 Prediction of the hub vortex instability in a wind turbine wake: stability analysis with eddy-viscosity models calibrated on wind tunnel data. J. Fluid Mech. 750, R1.CrossRefGoogle Scholar
Willert, C.E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10 (4), 181–193.CrossRefGoogle Scholar
Zhu, Y., Gupta, V. & Li, L.K.B. 2019 Coherence resonance in low-density jets. J. Fluid Mech. 881, R1.CrossRefGoogle Scholar