Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-25T08:24:56.072Z Has data issue: false hasContentIssue false
  • English
  • Français

Slip length for longitudinal shear flow over an arbitrary-protrusion-angle bubble mattress: the small-solid-fraction singularity

Published online by Cambridge University Press:  12 May 2017

Ory Schnitzer Open the ORCID record for Ory Schnitzer [Opens in a new window]
Ory Schnitzer*
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK
*
†Email address for correspondence: o.schnitzer@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the effective slip length for unidirectional flow over a superhydrophobic mattress of bubbles in the small-solid-fraction limit 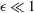$\unicode[STIX]{x1D716}\ll 1$. Using scaling arguments and utilising an ideal-flow analogy we elucidate the singularity of the slip length as 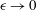$\unicode[STIX]{x1D716}\rightarrow 0$: relative to the periodicity it scales as 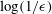$\log (1/\unicode[STIX]{x1D716})$ for protrusion angles 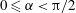$0\leqslant \unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/2$ and as 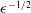$\unicode[STIX]{x1D716}^{-1/2}$ for 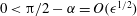$0<\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D6FC}=O(\unicode[STIX]{x1D716}^{1/2})$. We continue with a detailed asymptotic analysis using the method of matched asymptotic expansions, where ‘inner’ solutions valid close to the solid segments are matched with ‘outer’ solutions valid on the scale of the periodicity, where the bubbles protruding from the solid grooves appear to touch. The analysis yields asymptotic expansions for the effective slip length in each of the protrusion-angle regimes. These expansions overlap for intermediate protrusion angles, which allows us to form a uniformly valid approximation for arbitrary protrusion angles 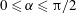$0\leqslant \unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x03C0}/2$. We thereby explicitly describe the transition with increasing protrusion angle from a logarithmic to an algebraic small-solid-fraction slip-length singularity.

JFM classification

Flow Control: Drag reduction Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: Microfluidics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 580 - 603
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ablowitz, M. J. & Fokas, A. S. 2003 Complex Variables: Introduction and Applications. Cambridge University Press.Google Scholar
Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions. Dover.Google Scholar
Choi, C.-H. & Kim, C.-J. 2006 Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96 (6), 066001.Google Scholar
Choi, C.-H., Westin, K. J. A. & Breuer, K. S. 2003 Apparent slip flows in hydrophilic and hydrophobic microchannels. Phys. Fluids 15 (10), 2897–2902.Google Scholar
Cottin-Bizonne, C., Barrat, J.-L., Bocquet, L. & Charlaix, E. 2003 Low-friction flows of liquid at nanopatterned interfaces. Nat. Mater. 2 (4), 237–240.CrossRefGoogle ScholarPubMed
Crowdy, D. 2010 Slip length for longitudinal shear flow over a dilute periodic mattress of protruding bubbles. Phys. Fluids 22 (12), 121703.Google Scholar
Crowdy, D. 2011a Frictional slip lengths and blockage coefficients. Phys. Fluids 23 (9), 091703.Google Scholar
Crowdy, D. 2011b Frictional slip lengths for unidirectional superhydrophobic grooved surfaces. Phys. Fluids 23 (7), 072001.Google Scholar
Crowdy, D. 2015a Effective slip lengths for longitudinal shear flow over partial-slip circular bubble mattresses. Fluid Dyn. Res. 47 (6), 065507.Google Scholar
Crowdy, D. 2015b A transform method for Laplace’s equation in multiply connected circular domains. IMA J. Appl. Maths 80 (6), 1902–1931.Google Scholar
Crowdy, D. G. 2016 Analytical formulae for longitudinal slip lengths over unidirectional superhydrophobic surfaces with curved menisci. J. Fluid Mech. 791, R7.Google Scholar
Davis, A. M. J. & Lauga, E. 2009 Geometric transition in friction for flow over a bubble mattress. Phys. Fluids 21 (1), 011701.Google Scholar
Davis, A. M. J. & Lauga, E. 2010 Hydrodynamic friction of fakir-like superhydrophobic surfaces. J. Fluid Mech. 661, 402–411.Google Scholar
Haase, A. S., Wood, J. A., Lammertink, R. G. & Snoeijer, J. H. 2016 Why bumpy is better: the role of the dissipation distribution in slip flow over a bubble mattress. Phys. Rev. Fluids 1 (5), 054101.Google Scholar
Hyväluoma, J. & Harting, J. 2008 Slip flow over structured surfaces with entrapped microbubbles. Phys. Rev. Lett. 100 (24), 246001.CrossRefGoogle ScholarPubMed
Kamrin, K., Bazant, M. Z. & Stone, H. A. 2010 Effective slip boundary conditions for arbitrary periodic surfaces: the surface mobility tensor. J. Fluid Mech. 658, 409–437.Google Scholar
Karatay, E., Haase, A. S., Visser, C. W., Sun, C., Lohse, D., Tsai, P. A. & Lammertink, R. G. H. 2013 Control of slippage with tunable bubble mattresses. Proc. Natl Acad. Sci. USA 110 (21), 8422–8426.Google Scholar
Koishi, T., Yasuoka, K., Fujikawa, S., Ebisuzaki, T. & Zeng, X. C. 2009 Coexistence and transition between cassie and wenzel state on pillared hydrophobic surface. Proc. Natl Acad. Sci. USA 106 (21), 8435–8440.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Lee, C. & Choi, C.-H. 2008 Structured surfaces for a giant liquid slip. Phys. Rev. Lett. 101 (6), 064501.CrossRefGoogle ScholarPubMed
Luca, E., Marshall, J. S. & Karamanis, G.2017 Longitudinal shear flow over a bubble mattress with curved menisci: arbitrary protrusion angle and solid fraction. In preparation.Google Scholar
Morris, S. J. S. 2003 The evaporating meniscus in a channel. J. Fluid Mech. 494, 297–317.Google Scholar
Nehari, Z. 1975 Conformal Mapping. Courier Corporation.Google Scholar
Ng, C.-O. & Wang, C. Y. 2010 Apparent slip arising from stokes shear flow over a bidimensional patterned surface. Microfluid. Nanofluid. 8 (3), 361–371.Google Scholar
Nizkaya, T. V., Dubov, A. L., Mourran, A. & Vinogradova, O. I. 2016 Probing effective slippage on superhydrophobic stripes by atomic force microscopy. Soft Matt. 12, 6910–6917.Google Scholar
Philip, J. R. 1972 Flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23 (3), 353–372.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Sbragaglia, M. & Prosperetti, A. 2007 A note on the effective slip properties for microchannel flows with ultrahydrophobic surfaces. Phys. Fluids 19 (4), 043603.Google Scholar
Schnitzer, O. 2016 Singular effective slip length for longitudinal flow over a dense bubble mattress. Phys. Rev. Fluids 1, 052101(R).Google Scholar
Schönecker, C., Baier, T. & Hardt, S. 2014 Influence of the enclosed fluid on the flow over a microstructured surface in the cassie state. J. Fluid Mech. 740, 168–195.Google Scholar
Schönecker, C. & Hardt, S. 2013 Longitudinal and transverse flow over a cavity containing a second immiscible fluid. J. Fluid Mech. 717, 376–394.CrossRefGoogle Scholar
Teo, C. J. & Khoo, B. C. 2010 Flow past superhydrophobic surfaces containing longitudinal grooves: effects of interface curvature. Microfluid. Nanofluid. 9 (2‐3), 499–511.Google Scholar
Truesdell, R., Mammoli, A., Vorobieff, P., van Swol, F. & Brinker, C. J. 2006 Drag reduction on a patterned superhydrophobic surface. Phys. Rev. Lett. 97 (4), 044504.Google Scholar
Wexler, J. S., Jacobi, I. & Stone, H. A. 2015 Shear-driven failure of liquid-infused surfaces. Phys. Rev. Lett. 114 (16), 168301.Google Scholar
Yariv, E. & Sherwood, J. D. 2015 Application of Schwarz–Christoffel mapping to the analysis of conduction through a slot. Proc. R. Soc. Lond. A 471, 20150292.Google Scholar
Ybert, C., Barentin, C., Cottin-Bizonne, C., Joseph, P. & Bocquet, L. 2007 Achieving large slip with superhydrophobic surfaces: scaling laws for generic geometries. Phys. Fluids 19 (12), 123601.Google Scholar