Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-27T20:21:42.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock–turbulence interactions at high turbulence intensities

Published online by Cambridge University Press:  14 May 2019

Chang Hsin Chen  and
Diego A. Donzis Open the ORCID record for Diego A. Donzis [Opens in a new window]
Chang Hsin Chen
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
Diego A. Donzis*
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843, USA
*
†Email address for correspondence: donzis@tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

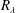Shock–turbulence interactions are investigated using well-resolved direct numerical simulations (DNS) and analysis at a range of Reynolds, mean and turbulent Mach numbers ($R_{\unicode[STIX]{x1D706}}$, 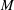$M$ and 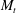$M_{t}$, respectively). The simulations are shock and turbulence resolving with 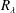$R_{\unicode[STIX]{x1D706}}$ up to 65, 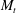$M_{t}$ up to 0.54 and 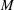$M$ up to 1.4. The focus is on the effect of strong turbulence on the jumps of mean thermodynamic variables across the shock, the shock structure and the amplification of turbulence as it moves through the shock. Theoretical results under the so-called quasi-equilibrium (QE) assumption provide explicit laws for a number of statistics of interests which are in agreement with the new DNS data presented here as well as all the data available in the literature. While in previous studies turbulence was found to weaken jumps, it is shown here that stronger jumps are also observed depending on the regime of the interaction. Statistics of the dilatation at the shock are also investigated and found to be well represented by QE for weak turbulence but saturate at high turbulence intensities with a Reynolds number dependence also captured by the analysis. Finally, amplification factors are found to present a universal behaviour with two limiting asymptotic regimes governed by 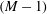$(M-1)$ and 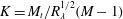$K=M_{t}/R_{\unicode[STIX]{x1D706}}^{1/2}(M-1)$, for weak and strong turbulence, respectively. Effect of anisotropy in the incoming flow is also assessed by utilizing two different forcing mechanisms to generate turbulence.

JFM classification

Turbulent Flows: Compressible turbulence Compressible Flows: Shock waves Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 813 - 847
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agui, J. H., Briassulis, G. & Andreopoulos, Y. 2005 Studies of interactions of a propagating shock wave with decaying grid turbulence: velocity and vorticity fields. J. Fluid Mech. 524, 143–195.Google Scholar
Andreopoulos, Y., Agui, J. H. & Briassulis, G. 2000 Shock wave–turbulence interactions. Annu. Rev. Fluid Mech. 32, 309–345.Google Scholar
Barenblatt, G. I. 2003 Scaling. Cambridge University Press.Google Scholar
Barre, S., Alem, D. & Bonnet, J. P. 1996 Experimental study of a normal shock/homogeneous turbulence interaction. AIAA J. 34, 968–974.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Boukharfane, R., Bouali, Z. & Mura, A. 2018 Evolution of scalar and velocity dynamics in planar shock–turbulence interaction. Shock Waves 28 (6), 1117–1141.Google Scholar
Chisnell, R. F. 1955 The normal motion of a shock wave through a non-uniform one-dimensional medium. Proc. R. Soc. Lond. A 232 (1190), 350–370.Google Scholar
Donzis, D. A. 2012a Amplification factors in shock–turbulence interactions: effect of shock thickness. Phys. Fluids 24, 011705.Google Scholar
Donzis, D. A. 2012b Shock structure in shock–turbulence interactions. Phys. Fluids 24, 126101.Google Scholar
Donzis, D. A. & Jagannathan, S. 2013 Fluctuations of thermodynamic variables in stationary compressible turbulence. J. Fluid Mech. 733, 221–244.Google Scholar
Freund, J. B. 1997 Proposed inflow/outflow boundary condition for direct computation of aerodynamic sound the vorticity jump across a shock in a non-uniform flow. AIAA J. 35 (4), 740–742.Google Scholar
Gatski, T. B. & Bonnet, J.-P. 2009 Compressibility, Turbulence and High Speed Flow. Elsevier.Google Scholar
Goldenfeld, N. 2006 Roughness-induced critical phenomena in a turbulent flow. Phys. Rev. Lett. 96, 044503.Google Scholar
Grant, H. L. & Nisbet, I. C. T. 1957 The inhomogeneity of grid turbulence. J. Fluid Mech. 2 (3), 263–272.Google Scholar
Hannappel, R. & Friedrich, R. 1995 Direct numerical-simulation of a Mach-2 shock interacting with isotropic turbulence. Appl. Sci. Res. 54, 205–221.Google Scholar
Hesselink, L. & Sturtevant, B. 1988 Propagation of weak shocks through a random medium. J. Fluid Mech. 196, 513–553.Google Scholar
Honkan, A. & Andreopoulos, J. 1992 Rapid compression of grid-generated turbulence by a moving shock-wave. Phys. Fluids 4 (11), 2562–2572.Google Scholar
Inokuma, K., Watanabe, T., Nagata, K., Sasoh, A. & Sakai, Y. 2017 Finite response time of shock wave modulation by turbulence. Phys. Fluids 29 (5), 051701.Google Scholar
Jacquin, L., Cambon, C. & Blin, E. 1993 Turbulence amplification by a shock wave and rapid distortion theory. Phys. Fluids 3, 2539.Google Scholar
Jagannathan, S. & Donzis, D. A. 2016 Reynolds and Mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations. J. Fluid Mech. 789, 669–707.Google Scholar
Jamme, S., Cazalbou, J.-B., Torres, F. & Chassaing, P. 2002 Direct numerical simulation of the interaction between a shock wave and various types of isotropic turbulence. Flow Turbul. Combust. 68, 227–268.Google Scholar
Jimenez, J. 1998 Turbulent velocity fluctuations need not be Gaussian. J. Fluid Mech. 376, 139–147.Google Scholar
Kitamura, T., Nagata, K., Sakai, Y. & Ito, Y. 2016 Rapid distortion theory analysis on the interaction between homogeneous turbulence and a planar shock wave. J. Fluid Mech. 802, 108–146.Google Scholar
Kovasznay, L. S. G. 1953 Turbulence in supersonic flow. J. Aerosp. Sci. 20 (10), 657–674.Google Scholar
Larsson, J., Bermejo-Moreno, I. & Lele, S. K. 2013 Reynolds- and Mach-number effects in canonical shock–turbulence interaction. J. Fluid Mech. 717, 293–321.Google Scholar
Larsson, J. & Lele, S. K. 2009 Direct numerical simulation of canonical shock/turbulence interaction. Phys. Fluids 21, 126101.Google Scholar
Lee, S., Lele, S. K. & Moin, P. 1993 Direct numerical simulation of isotropic turbulence interacting with a weak shock wave. J. Fluid Mech. 251, 533–562.Google Scholar
Lee, S., Lele, S. K. & Moin, P. 1997 Interaction of isotropic turbulence with shock waves: effect of shock strength. J. Fluid Mech. 340, 225–247.Google Scholar
Lele, S. K. 1992a Compact finite-difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Lele, S. K. 1992b Shock-jump relations in a turbulent flow. Phys. Fluids 4 (12), 2900–2905.Google Scholar
Livescu, D. & Ryu, J. 2016 Vorticity dynamics after the shock–turbulence interaction. Shock Waves 26 (3), 241–251.Google Scholar
Mahesh, K., Lee, S., Lele, S. K. & Moin, P. 1995 Interaction of an isotropic field of acoustic waves with a shock wave. J. Fluid Mech. 300, 383–407.Google Scholar
Mahesh, K., Lele, S. K. & Moin, P. 1997 The influence of entropy fluctuations on the interaction of turbulence with a shock wave. J. Fluid Mech. 334, 353–379.Google Scholar
Moeckel, W. E.1952 Interaction of oblique shock waves with regions of variable pressure, entropy, and energy. NACA TN-2725.Google Scholar
Mohamed, M. S. & Larue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. II. MIT Press.Google Scholar
Moore, F. K.1954 Unsteady oblique interaction of a shock wave with a plane disturbance. Tech. Rep. NACA Rep. 1165.Google Scholar
Moser, R. D. 2006 On the validity of the continuum approximation in high Reynolds number turbulence. Phys. Fluids 18 (7), 078105.Google Scholar
Noullez, A., Frisch, U., Wallace, G., Lempert, W. & Miles, R. B. 1997 Transverse velocity increments in turbulent flow using the relief technique. J. Fluid Mech. 339, 287–307.Google Scholar
Obukhov, A. M. 1949 The structure of the temperature field in a turbulent flow. Izv. Akad. Nauk. SSSR 13, 58–69.Google Scholar
Quadros, R., Sinha, K. & Larsson, J. 2016a Kovasznay mode decomposition of velocity–temperature correlation in canonical shock–turbulence interaction. Flow Turbul. Combust. 97, 787–810.Google Scholar
Quadros, R., Sinha, K. & Larsson, J. 2016b Turbulence energy flux generated by shock/homogeneous–turbulence interaction. J. Fluid Mech. 796, 113–157.Google Scholar
Ribner, H. S.1954a Convection of a pattern of vorticity through a shock wave. NACA TR-1164.Google Scholar
Ribner, H. S.1954b Shock–turbulence interaction and the generation of noise. NACA TR-1233.Google Scholar
Ryu, J. & Livescu, D. 2014 Turbulence structure behind the shock in canonical shock–vortical turbulence interaction. J. Fluid Mech. 756, R1.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
Schumacher, J., Scheel, J. D., Krasnov, D., Donzis, D. A., Yakhot, V. & Sreenivasan, K. R. 2014 Small-scale universality in fluid turbulence. Proc. Natl Acad. Sci. USA 111 (30), 10961–10965.Google Scholar
Schumacher, J., Sreenivasan, K. R. & Yakhot, V. 2007 Asymptotic exponents from low-Reynolds-number flows. New J. Phys. 9, 89.Google Scholar
Tanaka, K., Watanabe, T., Nagata, K., Sasoh, A., Sakai, Y. & Hayase, T. 2018 Amplification and attenuation of shock wave strength caused by homogeneous isotropic turbulence. Phys. Fluids 30 (3), 035105.Google Scholar
Taylor, G. I. 1935 Turbulence in a contracting stream. Z. Angew. Math. Mech. 15, 91–96.Google Scholar
Thompson, P. A. 1984 Compressible Fluid Dynamics. McGraw-Hill.Google Scholar
Velikovich, A. L., Huete, C. & Wouchuk, J. G. 2012 Effect of shock-generated turbulence on the Hugoniot jump conditions. Phys. Rev. E 85, 016301.Google Scholar
Whitham, G. B. 1958 On the propagation of shock waves through regions of non-uniform area or flow. J. Fluid Mech. 4 (4), 337–360.Google Scholar
Widom, B. 1965 Equation of state in the neighborhood of the critical point. J. Chem. Phys. 43 (11), 3898–3905.Google Scholar
Williams, J. E. F. & Howe, M. S. 1973 On the possibility of turbulent thickening of weak shock waves. J. Fluid Mech. 58 (3), 461–480.Google Scholar
Wouchuk, J. G., de Lira, C. H. R. & Velikovich, A. L. 2009 Analytical linear theory for the interaction of a planar shock wave with an isotropic turbulent vorticity field. Phys. Rev. E 79, 066315.Google Scholar
Yakhot, V. & Donzis, D. A. 2017 Emergence of multiscaling in a random-force stirred fluid. Phys. Rev. Lett. 119, 044501.Google Scholar
Yakhot, V. & Donzis, D. A. 2018 Anomalous exponents in strong turbulence. Phys. D 384‐385, 12–17.Google Scholar
Zank, G. P., Zhou, Y., Matthaeus, W. H. & Rice, W. K. M. 2002 The interaction of turbulence with shock waves: a basic model. Phys. Fluids 14, 3766–3774.Google Scholar
Zeldovich, Y. B. & Raizer, Y. P. 2002 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Dover.Google Scholar