Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T18:55:57.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Separation control and drag reduction for boat-tailed axisymmetric bodies through contoured transverse grooves

Published online by Cambridge University Press:  26 October 2017

A. Mariotti Open the ORCID record for A. Mariotti [Opens in a new window] ,
G. Buresti ,
G. Gaggini  and
M. V. Salvetti
A. Mariotti*
Affiliation:
Dipartimento di Ingegneria Civile e Industriale, Università di Pisa, Via G. Caruso 8, 56122 Pisa, Italy
G. Buresti
Affiliation:
Dipartimento di Ingegneria Civile e Industriale, Università di Pisa, Via G. Caruso 8, 56122 Pisa, Italy
G. Gaggini
Affiliation:
Dipartimento di Ingegneria Civile e Industriale, Università di Pisa, Via G. Caruso 8, 56122 Pisa, Italy
M. V. Salvetti
Affiliation:
Dipartimento di Ingegneria Civile e Industriale, Università di Pisa, Via G. Caruso 8, 56122 Pisa, Italy
*
†Email address for correspondence: alessandro.mariotti@for.unipi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the results of a numerical and experimental investigation aimed at assessing the performance of a control method to delay boundary layer separation consisting of the introduction on the surface of contoured transverse grooves, i.e. of small cavities with an appropriate shape orientated transverse to the incoming flow. The shape of the grooves and their depth – which must be significantly smaller than the thickness of the incoming boundary layer – are chosen so that the flow recirculations present within the grooves are steady and stable. This passive control strategy is applied to an axisymmetric bluff body with various rear boat tails, which are characterized by different degrees of flow separation. Variational multiscale large eddy simulations and wind tunnel tests are carried out. The Reynolds number, for both experiments and simulations, is 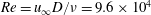$Re=u_{\infty }D/\unicode[STIX]{x1D708}=9.6\times 10^{4}$; due to the different incoming flow turbulence level, the boundary layer conditions before the boat tails are fully developed turbulent in the experiments and transitional in the simulations. In all cases, the introduction of one single axisymmetric groove in the lateral surface of the boat tails produces significant delay of the boundary layer separation, with consequent reduction of the pressure drag. Nonetheless, the wake dynamical structure remains qualitatively similar to the one typical of a blunt-based axisymmetric body, with quantitative variations that are consistent with the reduction in wake width caused by boat tailing and by the grooves. A few supplementary simulations show that the effect of the grooves is also robust to the variation of the geometrical parameters defining their shape. All the obtained data support the interpretation that the relaxation of the no-slip boundary condition for the flow surrounding the recirculation regions, with an appreciable velocity along their borders, is the physical mechanism responsible for the effectiveness of the present separation-control method.

JFM classification

Boundary Layers: Boundary layer separation Flow Control: Drag reduction Flow Control: Flow Control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 514 - 549
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barros, D., Borée, J., Noack, B. R., Spohn, A. & Ruiz, T. 2016 Bluff body drag manipulation using pulsed jets and coanda effect. J. Fluid Mech. 805, 422–459.Google Scholar
Bohorquez, P. & Parras, L. 2011 Three-dimensional numerical simulation of the wake flow of an afterbody at subsonic speeds. Theor. Comput. Fluid Dyn. 27, 201–218.CrossRefGoogle Scholar
Buresti, G. 2012 Elements of Fluid Dynamics. Imperial College Press.Google Scholar
Buresti, G. & Tondi, D.2007 Stepped boat-tails: a proposal for the control of the aerodynamic loads on bluff bodies. In Atti del dipartimento di Ingegneria Aerospaziale, $N^{\circ }$ ADIA 2007-7. ETS Editrice, Pisa.Google Scholar
Camarri, S., Salvetti, M. V., Koobus, B. & Dervieux, A. 2004 A low-diffusion MUSCL scheme for LES on unstructured grids. Comput. Fluids 33, 1101–1129.Google Scholar
Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.Google Scholar
Choi, H., Lee, J. & Park, H. 2014 Aerodynamics of heavy vehicles. Annu. Rev. Fluid Mech. 46, 441–468.CrossRefGoogle Scholar
Colonius, T.2001 An overview of simulation, modeling, and active control of flow/acoustic resonance in open cavities. AIAA Paper 2001-0076.Google Scholar
Gad-el-Hak, M. 2000 Flow Control: Passive, Active, and Reactive Flow Management. Cambridge University Press.Google Scholar
García de la Cruz, J. M., Oxlade, A. R. & Morrison, J. F. 2017 Passive control of base pressure on an axisymmetric blunt body using a perimetric slit. Phys. Rev. Fluids 2, 043905.Google Scholar
Gentile, V., van Oudheusden, B. W., Schrijer, F. F. J. & Scarano, F. 2017 The effect of angular misalignment on low-frequency axisymmetric wake instability. J. Fluid Mech. 813, R3.CrossRefGoogle Scholar
Gharib, M. & Roshko, A. 1987 The effect of flow oscillations on cavity drag. J. Fluid Mech. 177, 501–530.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2014 Statistical axisymmetry of the turbulent sphere wake. Exp. Fluids 55, 1838.Google Scholar
Grandemange, M., Gohlke, M., Parezanovic, V. & Cadot, O. 2012 On experimental sensitivity analysis of the turbulent wake from an axisymmetric blunt trailing edge. Phys. Fluids 24, 035106.Google Scholar
Heller, H. H. & Bliss, D. B.1975 The physical mechanism of flow induced pressure fluctuations in cavities and concepts for their supression. AIAA Paper 75-491.CrossRefGoogle Scholar
Howard, F. G. & Goodman, W. L. 1985 Axisymmetric bluff-body drag reduction through geometrical modification. J. Aircraft 22, 516–522.CrossRefGoogle Scholar
Howard, F. G., Goodman, W. L. & Walsh, M. J.1983 Axisymmetric bluff-body drag reduction using circumferential grooves. AIAA Paper 83-1788.CrossRefGoogle Scholar
Iollo, A. & Zannetti, L. 2001 Trapped vortex optimal control by suction and blowing at the wall. Eur. J. Mech. (B/Fluids) 20, 7–24.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jones, E. M.2013 An experimental study of flow separation over a flat plate with 2D transverse grooves. M.S. thesis, University of Alabama, Tuscaloosa, AL, USA.Google Scholar
Lang, A. W., Jones, E. M. & Afroz, F. 2017 Separation control over a grooved surface inspired by dolphin skin. Bioinspir. Biomim. 12, 026005.Google Scholar
Lasagna, D., Donelli, R., De Gregorio, F. & Iuso, G. 2011 Effects of a trapped vortex cell on a thick wing airfoil. Exp. Fluids 51, 1369–1384.CrossRefGoogle Scholar
Lasagna, D. & Iuso, G. 2016 Flow regimes in a trapped vortex cell. Exp. Fluids 57, 36.Google Scholar
Lin, J. C.1992 Control of low-speed turbulent separated flow over a backward-facing ramp. PhD thesis, Old Dominion University, Norfolk, VA. Also NASA-TM-109740.Google Scholar
Mair, W. A. 1969 Reduction of base drag by boat-tailed afterbodies in low-speed flow. Aeronaut. Q. XX, 307–320.Google Scholar
Margason, R. J.1996 Investigation of the effect of two-dimensional cavities on boundary layers in an adverse pressure gradient. PhD thesis, Naval Postgraduate School, Monterey, CA.Google Scholar
Mariotti, A. & Buresti, G. 2013 Experimental investigation on the influence of boundary layer thickness on the base pressure and near-wake flow features of an axisymmetric blunt-based body. Exp. Fluids 54, 1612.Google Scholar
Mariotti, A., Buresti, G. & Salvetti, M. V. 2014 Control of the turbulent flow in a plane diffuser through optimized contoured cavities. Eur. J. Mech. (B/Fluids) 48, 254–265.Google Scholar
Mariotti, A., Buresti, G. & Salvetti, M. V. 2015a Connection between base drag, separating boundary layer characteristics and wake mean recirculation length of an axisymmetric blunt-based body. J. Fluids Struct. 55, 191–203.Google Scholar
Mariotti, A., Buresti, G. & Salvetti, M. V. 2015b Use of multiple local recirculations to increase the efficiency in diffusers. Eur. J. Mech. (B/Fluids) 50, 27–37.Google Scholar
Mariotti, A., Grozescu, A. N., Buresti, G. & Salvetti, M. V. 2013 Separation control and efficiency improvement in a 2D diffuser by means of contoured cavities. Eur. J. Mech. (B/Fluids) 41, 138–149.CrossRefGoogle Scholar
Maull, D. J. & Hoole, B. J. 1967 The effect of boat-tailing on the flow round a two-dimensional blunt-based aerofoil at zero incidence. J. R. Aero. Soc. 71, 854–858.Google Scholar
Migay, V. K. 1962 The efficiency of a cross-ribbed curvilinear diffuser. Energomashinostroenie 1, 45–46; (English translation FTD–TT–62–1151).Google Scholar
Ouvrard, H., Koobus, B., Dervieux, A. & Salvetti, M. V. 2010 Classical and variational multiscale LES of the flow around a circular cylinder on unstructured grids. Comput. Fluids 39, 1083–1094.CrossRefGoogle Scholar
Pey, Y. Y. & Chua, L. P. 2014 Effects of trailing wall modifications on cavity wall pressure. Exp. Therm. Fluid Sci. 57, 250–260.CrossRefGoogle Scholar
Pey, Y. Y., Chua, L. P. & Siauw, W. L. 2014 Effect of trailing edge ramp on cavity flow and pressure drag. Intl J. Heat Fluid Flow 45, 53–71.Google Scholar
Reichardt, H. 1951 Vollstaendige Darstellung der turbulenten Geschwindigkeitsverteilung in glatten Leitungen. Z. Angew. Math. Mech. J. Appl. Math. Mech. 31, 208–219.Google Scholar
Rigas, G., Oxlade, A. R., Morgans, A. S. & Morrison, J. F. 2014 Low-dimensional dynamics of a turbulent axysymmetric wake. J. Fluid Mech. 755, R5.Google Scholar
Ringleb, F. 1961 Separation control by trapped vortices. In Boundary Layer and Flow Control (ed. Lachmann, G. V.), vol. 1, pp. 265–294. Pergamon.Google Scholar
Rockwell, D. & Naudascher, E. 1978 Review – self-sustaining oscillations of flow past cavities. Trans. ASME J. Fluids Engng 100, 152–165.Google Scholar
Rossiter, J. E.1964 Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Aero. Res. Counc. R&M, No. 3438. Her Majesty’s Stationery Office.Google Scholar
Rowley, C. W., Colonius, T. & Basu, A. J. 2002 On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities. J. Fluid Mech. 455, 315–346.Google Scholar
Sarohia, V.1975 Experimental and analytical investigation of oscillations in flows over cavities. PhD thesis, California Institute of Technology, CA, USA.CrossRefGoogle Scholar
Sarohia, V. 1977 Experimental investigation of oscillations in flows over shallow cavities. AIAA J. 15, 984–991.Google Scholar
Selby, G. V., Lin, J. C. & Howard, F. G. 1990 Turbulent flow separation control over a backward-facing ramp via transverse and swept grooves. Trans. ASME J. Fluids Engng 112, 238–240.CrossRefGoogle Scholar
Serrin, J. 1959 Mathematical principles of classical fluid mechanics. In Handbuch der Physik VIII/1 (ed. Flügge, S.), pp. 125–263. Springer.Google Scholar
Stull, F. D. & Velkoff, H. R.1972 Effect of transverse ribs on pressure recovery in two-dimensional subsonic diffusers. AIAA Paper 72-1141.Google Scholar
Taylor, Z. J., Gurka, R. & Kopp, G. A. 2014 Effects of leading edge geometry on the vortex shedding frequency of an elongated bluff body at high Reynolds numbers. J. Wind Engng Ind. Aerodyn. 128, 6675.Google Scholar
Tutty, O., Buffoni, M., Kerminbekov, R., Donelli, R., De Gregorio, F. & Rogers, E. 2013 Control of flow with trapped vortices: theory and experiments. Intl J. Flow Control 5, 89–110.Google Scholar
Vilaplana, G., Grandemange, M., Gohlke, M. & Cadot, O. 2013 Global mode of a sphere turbulent wake controlled by a small sphere. J. Fluids Struct. 41, 119–126.Google Scholar
Wong, D.-M & Mair, W. A. 1983 Boat-tailed afterbodies of square section as drag-reduction devices. J. Wind Engng Ind. Aerodyn. 12, 229–235.Google Scholar
Wornom, S., Ouvrard, H., Salvetti, M. V., Koobus, B. & Dervieux, A. 2011 Variational multiscale large-eddy simulations of the flow past a circular cylinder: Reynolds number effects. Comput. Fluids 47, 47–50.Google Scholar