1. Introduction: inclined layer convection
The phenomenon of thermal convection is known to all: warm fluid rises and cool fluid falls. But fluid cannot rise and fall in the same locations; the way in which the rising and falling locations are arranged in space provides the archetypal example of pattern formation. Reetz and coworkers (Reetz & Schneider Reference Reetz and Schneider2020; Reetz, Subramanian & Schneider Reference Reetz, Subramanian and Schneider2020) explore a generalization of Rayleigh–Bénard convection in which the confining plates held at different temperatures are inclined at an angle  $\gamma$ with respect to gravity. From a physical point of view, the immediate consequence is a shear flow in the direction of inclination, upwards along the warmer plate and downwards along the cooler one. From a mathematical point of view, the inclination renders the fluid layer anisotropic, distinguishing the direction of inclination and that perpendicular to it. As the Rayleigh number is increased, inclined convection undergoes a first transition from a featureless base state
$\gamma$ with respect to gravity. From a physical point of view, the immediate consequence is a shear flow in the direction of inclination, upwards along the warmer plate and downwards along the cooler one. From a mathematical point of view, the inclination renders the fluid layer anisotropic, distinguishing the direction of inclination and that perpendicular to it. As the Rayleigh number is increased, inclined convection undergoes a first transition from a featureless base state  $B$ to straight rolls. For compressed
$B$ to straight rolls. For compressed  $\textrm {CO}_2$ with a Prandtl number of 1.07, these rolls are buoyancy-driven, with axes parallel to the inclination (longitudinal rolls,
$\textrm {CO}_2$ with a Prandtl number of 1.07, these rolls are buoyancy-driven, with axes parallel to the inclination (longitudinal rolls,  $\textrm {LR}$, seen in the title figure) for
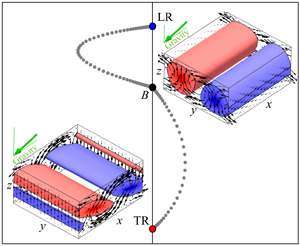
$\textrm {LR}$, seen in the title figure) for  $\gamma \lesssim 78^\circ$, and shear-driven, with axes perpendicular to the inclination (transverse rolls,
$\gamma \lesssim 78^\circ$, and shear-driven, with axes perpendicular to the inclination (transverse rolls,  $\textrm {TR}$, seen in the title figure) for
$\textrm {TR}$, seen in the title figure) for  $\gamma \gtrsim 78^\circ$ (e.g. Gershuni & Zhukhovitskii Reference Gershuni and Zhukhovitskii1969; Chen & Pearlstein Reference Chen and Pearlstein1989), as shown in figure 1. The limiting case in which the bounding plates are vertical (
$\gamma \gtrsim 78^\circ$ (e.g. Gershuni & Zhukhovitskii Reference Gershuni and Zhukhovitskii1969; Chen & Pearlstein Reference Chen and Pearlstein1989), as shown in figure 1. The limiting case in which the bounding plates are vertical ( $\gamma =90^\circ$) and the imposed temperature gradient is horizontal is sometimes called natural convection.
$\gamma =90^\circ$) and the imposed temperature gradient is horizontal is sometimes called natural convection.
The problem of inclined layer convection received a boost from experimental observations of exotic regimes such as crawling rolls and transverse bursts by Daniels and coworkers (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000; Daniels & Bodenschatz Reference Daniels and Bodenschatz2002; Daniels et al. Reference Daniels, Wiener and Bodenschatz2003). These were followed by numerical and theoretical simulations of these patterns by time stepping (Daniels et al. Reference Daniels, Brausch, Pesch and Bodenschatz2008) and by Floquet and Galerkin analyses (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016).
2. Overview: a numerical bifurcation study
Reetz and coworkers (Reetz & Schneider Reference Reetz and Schneider2020; Reetz et al. Reference Reetz, Subramanian and Schneider2020) have sought the bifurcation-theoretic origin of these exotic patterns. Their motivation is in part because of the features that inclined layer connection shares with wall-bounded shear flows such as plane Couette flow and pipe flow. These shear flows were not known to have any non-trivial solutions until their resistance to bifurcation-theoretic approaches was breached by Nagata (Reference Nagata1990) and Clever & Busse (Reference Clever and Busse1992), who continued solutions from Taylor–Couette flow and Rayleigh–Bénard convection to plane Couette flow. Shortly thereafter, travelling waves in pipe flow were computed by Faisst & Eckhardt (Reference Faisst and Eckhardt2003) and Wedin & Kerswell (Reference Wedin and Kerswell2004). Since then, dozens of solutions have been computed (e.g. Gibson, Halcrow & Cvitanović Reference Gibson, Halcrow and Cvitanović2008), all unstable.
These multiple solutions are thought to be of more than zoological interest, since Cvitanović & Eckhardt (Reference Cvitanović and Eckhardt1991) and Kawahara, Uhlmann & van Veen (Reference Kawahara, Uhlmann and van Veen2012) have proposed that turbulence in shear flows could be viewed as a collection of trajectories ricocheting between these multiple solutions via the connections between them. Indeed, for pipe flow, Hof et al. (Reference Hof, van Doorne, Westerweel, Nieuwstadt, Faisst, Eckhardt, Wedin, Kerswell and Waleffe2004) compared exact solutions with snapshots during the evolution of the flow.
Reetz & Schneider (Reference Reetz and Schneider2020) focus on several key states and dynamical regimes. One example is a sequence of bifurcations at  $\gamma =40^\circ$ from the base state to longitudinal rolls to wavy rolls to oblique wavy rolls. The oblique wavy rolls participate in a robust heteroclinic cycle, shown in figure 1. Reetz et al. (Reference Reetz, Subramanian and Schneider2020) expand on these results by surveying the parameter space of Rayleigh number and inclination angle to construct complete bifurcation diagrams and interpreting the transitions in the context of the large-aspect-ratio experiments. They have computed eight different invariant solutions all at Rayleigh number 21 266 and angle
$\gamma =40^\circ$ from the base state to longitudinal rolls to wavy rolls to oblique wavy rolls. The oblique wavy rolls participate in a robust heteroclinic cycle, shown in figure 1. Reetz et al. (Reference Reetz, Subramanian and Schneider2020) expand on these results by surveying the parameter space of Rayleigh number and inclination angle to construct complete bifurcation diagrams and interpreting the transitions in the context of the large-aspect-ratio experiments. They have computed eight different invariant solutions all at Rayleigh number 21 266 and angle  $\gamma =90^\circ$, where the longitudinal rolls (LR) do not exist: the transverse rolls (TR) already mentioned, and various periodically modulated versions of the longitudinal rolls. Carrying out direct numerical simulations at the same parameter values, they extracted snapshots that resembled these states, as shown in figure 2.
$\gamma =90^\circ$, where the longitudinal rolls (LR) do not exist: the transverse rolls (TR) already mentioned, and various periodically modulated versions of the longitudinal rolls. Carrying out direct numerical simulations at the same parameter values, they extracted snapshots that resembled these states, as shown in figure 2.
Figure 2. (a–h) Eight invariant states in vertical layer convection  $(\gamma =90^\circ )$, all at Rayleigh number 21 266, computed by continuation. (i–l) Four snapshots from direct numerical simulations of the turbulent regime at the same parameters. Adapted from Reetz et al. (Reference Reetz, Subramanian and Schneider2020).
$(\gamma =90^\circ )$, all at Rayleigh number 21 266, computed by continuation. (i–l) Four snapshots from direct numerical simulations of the turbulent regime at the same parameters. Adapted from Reetz et al. (Reference Reetz, Subramanian and Schneider2020).
3. Future: from bifurcation diagrams to turbulence?
There is no doubt that patterns and temporal behaviour are controlled and explained by the plethora of underlying dynamical objects – fixed points and travelling waves, periodic orbits and heteroclinic cycles. The ability to compute such objects for the full three-dimensional Navier–Stokes and Boussinesq equations has resulted from advances in several fields: first, the spectacular growth of dynamical systems theory and symmetry (e.g. the monographs by Golubitsky, Stewart & Schaeffer (Reference Golubitsky, Stewart and Schaeffer1988) and by Kuznetsov (Reference Kuznetsov1998)) following the discovery of deterministic chaos; second, the increasing power of computation; and third, the incorporation of matrix-free methods for linear algebra (Dijkstra et al. Reference Dijkstra, Wubs, Cliffe, Doedel, Dragomirescu, Eckhardt, Gelfgat, Hazel, Lucarini and Salinger2014) into algorithms for tracking dynamical objects. See, e.g., Marques et al. (Reference Marques, Mercader, Batiste and Lopez2007) and Boro\'nska & Tuckerman (Reference Borońska and Tuckerman2010) for computational bifurcation studies of convection. However, the application of the theories of Cvitanović & Eckhardt (Reference Cvitanović and Eckhardt1991) and Kawahara et al. (Reference Kawahara, Uhlmann and van Veen2012) to a turbulent hydrodynamic state would require the computation of an even larger number of dynamical objects, on a scale that is not yet possible. The challenge is to bridge the gap between bifurcation theory and the large-scale statistical phenomenon of turbulence.
Declaration of interests
The author reports no conflict of interest.

 $B$ to longitudinal rolls
$B$ to longitudinal rolls  $\textrm {LR}$ to wavy rolls
$\textrm {LR}$ to wavy rolls  $\textrm {WR}$ (inset i), followed by a sequence of widening oscillations leading to a heteroclinic cycle between the oblique wavy roll state
$\textrm {WR}$ (inset i), followed by a sequence of widening oscillations leading to a heteroclinic cycle between the oblique wavy roll state  $\textrm {OWR}$ and its image under a shift
$\textrm {OWR}$ and its image under a shift  $\tau _{xy}$ in
$\tau _{xy}$ in  $x$ and
$x$ and  $y$ (inset ii). The trajectory is projected onto the coordinates
$y$ (inset ii). The trajectory is projected onto the coordinates  $(D/I,I)$, where
$(D/I,I)$, where  $D$ is the viscous dissipation and
$D$ is the viscous dissipation and  $I$ is the energy input. (b) Temperature isosurfaces of
$I$ is the energy input. (b) Temperature isosurfaces of  $\textrm {WR}$ and
$\textrm {WR}$ and  $\textrm {OWR}$. Adapted from Reetz & Schneider (2020).
$\textrm {OWR}$. Adapted from Reetz & Schneider (2020).
 $(\gamma =90^\circ )$, all at Rayleigh number 21 266, computed by continuation. (i–l) Four snapshots from direct numerical simulations of the turbulent regime at the same parameters. Adapted from Reetz et al. (2020).
$(\gamma =90^\circ )$, all at Rayleigh number 21 266, computed by continuation. (i–l) Four snapshots from direct numerical simulations of the turbulent regime at the same parameters. Adapted from Reetz et al. (2020).


1. Introduction: inclined layer convection
The phenomenon of thermal convection is known to all: warm fluid rises and cool fluid falls. But fluid cannot rise and fall in the same locations; the way in which the rising and falling locations are arranged in space provides the archetypal example of pattern formation. Reetz and coworkers (Reetz & Schneider Reference Reetz and Schneider2020; Reetz, Subramanian & Schneider Reference Reetz, Subramanian and Schneider2020) explore a generalization of Rayleigh–Bénard convection in which the confining plates held at different temperatures are inclined at an angle $\gamma$ with respect to gravity. From a physical point of view, the immediate consequence is a shear flow in the direction of inclination, upwards along the warmer plate and downwards along the cooler one. From a mathematical point of view, the inclination renders the fluid layer anisotropic, distinguishing the direction of inclination and that perpendicular to it. As the Rayleigh number is increased, inclined convection undergoes a first transition from a featureless base state
$\gamma$ with respect to gravity. From a physical point of view, the immediate consequence is a shear flow in the direction of inclination, upwards along the warmer plate and downwards along the cooler one. From a mathematical point of view, the inclination renders the fluid layer anisotropic, distinguishing the direction of inclination and that perpendicular to it. As the Rayleigh number is increased, inclined convection undergoes a first transition from a featureless base state  $B$ to straight rolls. For compressed
$B$ to straight rolls. For compressed  $\textrm {CO}_2$ with a Prandtl number of 1.07, these rolls are buoyancy-driven, with axes parallel to the inclination (longitudinal rolls,
$\textrm {CO}_2$ with a Prandtl number of 1.07, these rolls are buoyancy-driven, with axes parallel to the inclination (longitudinal rolls,  $\textrm {LR}$, seen in the title figure) for
$\textrm {LR}$, seen in the title figure) for  $\gamma \lesssim 78^\circ$, and shear-driven, with axes perpendicular to the inclination (transverse rolls,
$\gamma \lesssim 78^\circ$, and shear-driven, with axes perpendicular to the inclination (transverse rolls,  $\textrm {TR}$, seen in the title figure) for
$\textrm {TR}$, seen in the title figure) for  $\gamma \gtrsim 78^\circ$ (e.g. Gershuni & Zhukhovitskii Reference Gershuni and Zhukhovitskii1969; Chen & Pearlstein Reference Chen and Pearlstein1989), as shown in figure 1. The limiting case in which the bounding plates are vertical (
$\gamma \gtrsim 78^\circ$ (e.g. Gershuni & Zhukhovitskii Reference Gershuni and Zhukhovitskii1969; Chen & Pearlstein Reference Chen and Pearlstein1989), as shown in figure 1. The limiting case in which the bounding plates are vertical ( $\gamma =90^\circ$) and the imposed temperature gradient is horizontal is sometimes called natural convection.
$\gamma =90^\circ$) and the imposed temperature gradient is horizontal is sometimes called natural convection.
Figure 1. (a) Evolution from base state $B$ to longitudinal rolls
$B$ to longitudinal rolls  $\textrm {LR}$ to wavy rolls
$\textrm {LR}$ to wavy rolls  $\textrm {WR}$ (inset i), followed by a sequence of widening oscillations leading to a heteroclinic cycle between the oblique wavy roll state
$\textrm {WR}$ (inset i), followed by a sequence of widening oscillations leading to a heteroclinic cycle between the oblique wavy roll state  $\textrm {OWR}$ and its image under a shift
$\textrm {OWR}$ and its image under a shift  $\tau _{xy}$ in
$\tau _{xy}$ in  $x$ and
$x$ and  $y$ (inset ii). The trajectory is projected onto the coordinates
$y$ (inset ii). The trajectory is projected onto the coordinates  $(D/I,I)$, where
$(D/I,I)$, where  $D$ is the viscous dissipation and
$D$ is the viscous dissipation and  $I$ is the energy input. (b) Temperature isosurfaces of
$I$ is the energy input. (b) Temperature isosurfaces of  $\textrm {WR}$ and
$\textrm {WR}$ and  $\textrm {OWR}$. Adapted from Reetz & Schneider (Reference Reetz and Schneider2020).
$\textrm {OWR}$. Adapted from Reetz & Schneider (Reference Reetz and Schneider2020).
The problem of inclined layer convection received a boost from experimental observations of exotic regimes such as crawling rolls and transverse bursts by Daniels and coworkers (Daniels et al. Reference Daniels, Plapp and Bodenschatz2000; Daniels & Bodenschatz Reference Daniels and Bodenschatz2002; Daniels et al. Reference Daniels, Wiener and Bodenschatz2003). These were followed by numerical and theoretical simulations of these patterns by time stepping (Daniels et al. Reference Daniels, Brausch, Pesch and Bodenschatz2008) and by Floquet and Galerkin analyses (Subramanian et al. Reference Subramanian, Brausch, Daniels, Bodenschatz, Schneider and Pesch2016).
2. Overview: a numerical bifurcation study
Reetz and coworkers (Reetz & Schneider Reference Reetz and Schneider2020; Reetz et al. Reference Reetz, Subramanian and Schneider2020) have sought the bifurcation-theoretic origin of these exotic patterns. Their motivation is in part because of the features that inclined layer connection shares with wall-bounded shear flows such as plane Couette flow and pipe flow. These shear flows were not known to have any non-trivial solutions until their resistance to bifurcation-theoretic approaches was breached by Nagata (Reference Nagata1990) and Clever & Busse (Reference Clever and Busse1992), who continued solutions from Taylor–Couette flow and Rayleigh–Bénard convection to plane Couette flow. Shortly thereafter, travelling waves in pipe flow were computed by Faisst & Eckhardt (Reference Faisst and Eckhardt2003) and Wedin & Kerswell (Reference Wedin and Kerswell2004). Since then, dozens of solutions have been computed (e.g. Gibson, Halcrow & Cvitanović Reference Gibson, Halcrow and Cvitanović2008), all unstable.
These multiple solutions are thought to be of more than zoological interest, since Cvitanović & Eckhardt (Reference Cvitanović and Eckhardt1991) and Kawahara, Uhlmann & van Veen (Reference Kawahara, Uhlmann and van Veen2012) have proposed that turbulence in shear flows could be viewed as a collection of trajectories ricocheting between these multiple solutions via the connections between them. Indeed, for pipe flow, Hof et al. (Reference Hof, van Doorne, Westerweel, Nieuwstadt, Faisst, Eckhardt, Wedin, Kerswell and Waleffe2004) compared exact solutions with snapshots during the evolution of the flow.
Reetz & Schneider (Reference Reetz and Schneider2020) focus on several key states and dynamical regimes. One example is a sequence of bifurcations at $\gamma =40^\circ$ from the base state to longitudinal rolls to wavy rolls to oblique wavy rolls. The oblique wavy rolls participate in a robust heteroclinic cycle, shown in figure 1. Reetz et al. (Reference Reetz, Subramanian and Schneider2020) expand on these results by surveying the parameter space of Rayleigh number and inclination angle to construct complete bifurcation diagrams and interpreting the transitions in the context of the large-aspect-ratio experiments. They have computed eight different invariant solutions all at Rayleigh number 21 266 and angle
$\gamma =40^\circ$ from the base state to longitudinal rolls to wavy rolls to oblique wavy rolls. The oblique wavy rolls participate in a robust heteroclinic cycle, shown in figure 1. Reetz et al. (Reference Reetz, Subramanian and Schneider2020) expand on these results by surveying the parameter space of Rayleigh number and inclination angle to construct complete bifurcation diagrams and interpreting the transitions in the context of the large-aspect-ratio experiments. They have computed eight different invariant solutions all at Rayleigh number 21 266 and angle  $\gamma =90^\circ$, where the longitudinal rolls (LR) do not exist: the transverse rolls (TR) already mentioned, and various periodically modulated versions of the longitudinal rolls. Carrying out direct numerical simulations at the same parameter values, they extracted snapshots that resembled these states, as shown in figure 2.
$\gamma =90^\circ$, where the longitudinal rolls (LR) do not exist: the transverse rolls (TR) already mentioned, and various periodically modulated versions of the longitudinal rolls. Carrying out direct numerical simulations at the same parameter values, they extracted snapshots that resembled these states, as shown in figure 2.
Figure 2. (a–h) Eight invariant states in vertical layer convection $(\gamma =90^\circ )$, all at Rayleigh number 21 266, computed by continuation. (i–l) Four snapshots from direct numerical simulations of the turbulent regime at the same parameters. Adapted from Reetz et al. (Reference Reetz, Subramanian and Schneider2020).
$(\gamma =90^\circ )$, all at Rayleigh number 21 266, computed by continuation. (i–l) Four snapshots from direct numerical simulations of the turbulent regime at the same parameters. Adapted from Reetz et al. (Reference Reetz, Subramanian and Schneider2020).
3. Future: from bifurcation diagrams to turbulence?
There is no doubt that patterns and temporal behaviour are controlled and explained by the plethora of underlying dynamical objects – fixed points and travelling waves, periodic orbits and heteroclinic cycles. The ability to compute such objects for the full three-dimensional Navier–Stokes and Boussinesq equations has resulted from advances in several fields: first, the spectacular growth of dynamical systems theory and symmetry (e.g. the monographs by Golubitsky, Stewart & Schaeffer (Reference Golubitsky, Stewart and Schaeffer1988) and by Kuznetsov (Reference Kuznetsov1998)) following the discovery of deterministic chaos; second, the increasing power of computation; and third, the incorporation of matrix-free methods for linear algebra (Dijkstra et al. Reference Dijkstra, Wubs, Cliffe, Doedel, Dragomirescu, Eckhardt, Gelfgat, Hazel, Lucarini and Salinger2014) into algorithms for tracking dynamical objects. See, e.g., Marques et al. (Reference Marques, Mercader, Batiste and Lopez2007) and Boro\'nska & Tuckerman (Reference Borońska and Tuckerman2010) for computational bifurcation studies of convection. However, the application of the theories of Cvitanović & Eckhardt (Reference Cvitanović and Eckhardt1991) and Kawahara et al. (Reference Kawahara, Uhlmann and van Veen2012) to a turbulent hydrodynamic state would require the computation of an even larger number of dynamical objects, on a scale that is not yet possible. The challenge is to bridge the gap between bifurcation theory and the large-scale statistical phenomenon of turbulence.
Declaration of interests
The author reports no conflict of interest.