Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-18T07:54:40.931Z Has data issue: false hasContentIssue false
  • English
  • Français

A reduced model for a phoretic swimmer

Published online by Cambridge University Press:  18 November 2022

A. Farutin ,
M.S. Rizvi Open the ORCID record for M.S. Rizvi [Opens in a new window] ,
W.-F. Hu ,
T.S. Lin Open the ORCID record for T.S. Lin [Opens in a new window] ,
S. Rafaï  and
C. Misbah Open the ORCID record for C. Misbah [Opens in a new window]
A. Farutin
Affiliation:
University of Grenoble Alpes, CNRS, LIPhy, F-38000 Grenoble, France
M.S. Rizvi
Affiliation:
University of Grenoble Alpes, CNRS, LIPhy, F-38000 Grenoble, France
W.-F. Hu
Affiliation:
Department of Mathematics, National Central University, Taoyuan 32001, Taiwan
T.S. Lin
Affiliation:
Department of Applied Mathematics, National Yang Ming Chiao Tung University, Hsinchu 30010, Taiwan
S. Rafaï
Affiliation:
University of Grenoble Alpes, CNRS, LIPhy, F-38000 Grenoble, France
C. Misbah*
Affiliation:
University of Grenoble Alpes, CNRS, LIPhy, F-38000 Grenoble, France
*
†Email address for correspondence: chaouqi.misbah@univ-grenoble-alpes.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

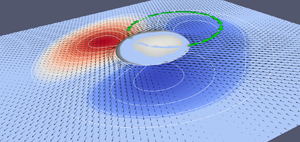
We consider a two-dimensional (2-D) model of an autophoretic particle. Beyond a certain emission/absorption rate (characterized by a dimensionless Péclet number, $Pe$) the particle is known to undergo a bifurcation from a non-motile to a motile state, with different trajectories, going from a straight to a chaotic motion by increasing $Pe$. From the full model, we derive a reduced closed model which involves only two time-dependent complex amplitudes $C_1(t)$ and $C_2(t)$ corresponding to the first two Fourier modes of the solute concentration field. It consists of two coupled nonlinear ordinary differential equations for $C_1$ and $C_2$ and presents several advantages: (i) the straight and circular motions can be handled fully analytically; (ii) complex motions such as chaos can be analysed numerically very efficiently in comparison with the numerically expensive full model involving partial differential equations; (iii) the reduced model has a universal form dictated only by symmetries (meaning that the form of the equations does not depend on a given phoretic model); (iv) the model can be extended to higher Fourier modes. The derivation method is exemplified for a 2-D model, for simplicity, but can easily be extended to three dimensions, not only for the presently selected phoretic model, but also for any model in which chemical activity triggers locomotion. A typical example can be found, for example, in the field of cell motility involving acto-myosin kinetics. This strategy offers an interesting way to cope with swimmers on the basis of ordinary differential equations, allowing for analytical tractability and efficient numerical treatment.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Biological Fluid Dynamics: Swimming/flying Complex Fluids: Active matter
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , A6
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Biomedical Engineering, Indian Institute of Technology Hyderabad, Kandi, Sangareddy, 502285, Telangana, India.

References

Callan-Jones, A.C., Ruprecht, V., Wieser, S., Heisenberg, C.P. & Voituriez, R. 2016 Cortical flow-driven shapes of nonadherent cells. Phys. Rev. Lett. 116, 028102.CrossRefGoogle ScholarPubMed
Chen, Y., Chong, K.L., Liu, L., Verzicco, R. & Lohse, D. 2021 Instabilities driven by diffusiophoretic flow on catalytic surfaces. J. Fluid Mech. 919, A10.CrossRefGoogle Scholar
Dauby, P.C., Desaive, T., Bragard, J. & Cerisier, P. 2001 Amplitude equations for Rayleigh–Bénard convective rolls far from threshold. Phys. Rev. E 64, 066301.CrossRefGoogle ScholarPubMed
Farutin, A., Etienne, J., Misbah, C. & Récho, P. 2019 Crawling in a fluid. Phys. Rev. Lett. 123, 118101.CrossRefGoogle Scholar
Farutin, A. & Misbah, C. 2021 Singular bifurcations: a regularization theory. arXiv:2112.12094.Google Scholar
Hawkins, R.J., Poincloux, R., Bénichou, O., Piel, M., Chavrier, P. & Voituriez, R. 2011 Spontaneous contractility-mediated cortical flow generates cell migration in three-dimensional environments. Biophys. J. 101 (5), 1041–1045.CrossRefGoogle ScholarPubMed
Hokmabad, B.V., Dey, R., Jalaal, M., Mohanty, D., Almukambetova, M., Baldwin, K.A., Lohse, D. & Maass, C.C. 2021 Emergence of bimodal motility in active droplets. Phys. Rev. X 11, 011043.Google Scholar
Hu, W.-F., Lin, T.S., Rafai, S. & Chaouqi, M. 2022 Spontaneous locomotion of phoretic particles in three dimensions. Phys. Rev. Fluids 7, 03400.CrossRefGoogle Scholar
Hu, W.F., Lin, T.S., Rafai, S. & Misbah, C. 2019 Chaotic swimming of phoretic particles. Phys. Rev. Lett. 123, 238004.CrossRefGoogle ScholarPubMed
Izri, Z., Van Der Linden, M.N., Michelin, S. & Dauchot, O. 2014 Self-propulsion of pure water droplets by spontaneous marangoni-stress-driven motion. Phys. Rev. Lett. 113 (24), 248302.CrossRefGoogle ScholarPubMed
Izzet, A., Moerman, P.G., Gross, P., Groenewold, J., Hollingsworth, A.D., Bibette, J. & Brujic, J. 2020 Tunable persistent random walk in swimming droplets. Phys. Rev. X 10, 021035.Google Scholar
Jin, C., Krüger, C. & Maass, C.C. 2017 Chemotaxis and autochemotaxis of self-propelling droplet swimmers. Proc. Natl Acad. Sci. 114 (20), 5089–5094.CrossRefGoogle ScholarPubMed
Li, G. 2022 Swimming dynamics of a self-propelled droplet. J. Fluid Mech. 934, A20.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2014 Phoretic self-propulsion at finite peclet numbers. J. Fluid Mech. 747, 572–604.CrossRefGoogle Scholar
Michelin, S., Lauga, E. & Bartolo, D. 2013 Spontaneous autophoretic motion of isotropic particles. Phys. Fluids 25, 061701.CrossRefGoogle Scholar
Misbah, C., Rizvi, M.S., Hu, W.-F., Lin, T.S., Rafai, S. & Farutin, A. 2021 Universal trajectories of motile particles driven by chemical activity. arXiv:2112.13801.Google Scholar
Morozov, M. 2020 Adsorption inhibition by swollen micelles may cause multistability in active droplets. Soft Matt. 16, 5624–5632.CrossRefGoogle ScholarPubMed
Morozov, M. & Michelin, S. 2019 a Nonlinear dynamics of a chemically-active drop: from steady to chaotic self-propulsion. J. Chem. Phys. 150 (4), 044110.CrossRefGoogle ScholarPubMed
Morozov, M. & Michelin, S. 2019 b Self-propulsion near the onset of marangoni instability of deformable active droplets. J. Fluid Mech. 860, 711–738.CrossRefGoogle Scholar
Rednikov, A.Y., Ryazantsev, Y.S. & Velarde, M.G. 1994 Drop motion with surfactant transfer in a homogeneous surrounding. Phys. Fluids 6 (2), 451–468.CrossRefGoogle Scholar
Schmitt, M. & Stark, H. 2013 Swimming active droplet: a theoretical analysis. Eur. Phys. Lett. 101 (4), 44008.CrossRefGoogle Scholar