Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T10:28:45.047Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-geostrophic vortex solutions over isolated topography

Published online by Cambridge University Press:  17 March 2021

Jeasson F. Gonzalez Open the ORCID record for Jeasson F. Gonzalez [Opens in a new window]  and
L. Zavala Sansón Open the ORCID record for L. Zavala Sansón [Opens in a new window]
Jeasson F. Gonzalez
Affiliation:
Department of Physical Oceanography, CICESE, Ensenada 22860, Mexico
L. Zavala Sansón*
Affiliation:
Department of Physical Oceanography, CICESE, Ensenada 22860, Mexico
*
†Email address for correspondence: lzavala@cicese.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

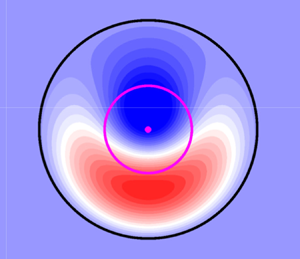
Analytical solutions of barotropic, quasi-geostrophic vortices over an axisymmetric bottom topography are presented. The solutions are based on independent azimuthal modes adapted to the shape of the topography. Modes 0 (circular monopoles) and 1 (asymmetric dipoles) are evaluated for different topographic profiles that represent either submarine mountains or valleys. The interior fields are matched with an exterior flow with streamlines enclosing the vortices, so the structures remain trapped over the topographic feature. The solutions are steady in a reference frame attached to the rotation of the vortices around the topography. The main features of trapped vortices as a function of the topographic parameters, such as the structure, strength and angular speed, are discussed through numerical simulations initialised with theoretical vorticity fields. The model results reproduce reasonably well the analytical solutions when the topographic effects are strong enough to inhibit the dipole self-propagation. In contrast, very intense dipolar modes may escape from the influence of the topography.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Topographic effects Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A64
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Batchelor, G.K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Carnevale, G.F., Kloosterziel, R.C. & van Heijst, G.J.F. 1991 Propagation of barotropic vortices over topography in a rotating tank. J. Fluid Mech. 233, 119–139.CrossRefGoogle Scholar
Carnevale, G.F., Purini, R., Orlandi, P. & Cavazza, P. 1995 Barotropic quasi-geostrophic $f$-plane flow over anisotropic topography. J. Fluid Mech. 285, 329–347.CrossRefGoogle Scholar
Chaplygin, S.A. 1903 One case of vortex motion in fluid. Trans. Phys. Sect. Imperial Moscow Soc. R. Soc. Lond. A 175, 363–410.Google Scholar
Flierl, G.R., Stern, M.E. & Whitehead, J.A. 1983 The physical significance of modons: laboratory experiments and general integral constraints. Dyn. Atmos. Oceans 7 (4), 233–263.CrossRefGoogle Scholar
Grimshaw, R., He, X. & Broutman, D. 1994 Analytical and numerical study of a barotropic eddy on a topographic slope. J. Phys. Oceangr. 24 (7), 1587–1607.2.0.CO;2>CrossRefGoogle Scholar
Hide, R. 1961 Origin of Jupiter's great red spot. Nature 190, 895–896.CrossRefGoogle Scholar
Huppert, H.E. & Bryan, K. 1976 Topographically generated eddies. Deep-Sea Res. 23, 655–679.Google Scholar
Makarov, V.G. 2012 Dipole evolution in rotating two-dimensional flow with bottom friction. Phys. Fluids 24 (2), 026602.CrossRefGoogle Scholar
Meleshko, V.V. & van Heijst, G.J.F. 1994 On Chaplygin's investigations of two-dimensional vortex structures in an inviscid fluid. J. Fluid Mech. 272, 157–182.CrossRefGoogle Scholar
Rhines, P.B. 1969 Slow oscillations in an ocean of varying depth. Part 2. Islands and seamounts. J. Fluid Mech. 37 (1), 191–205.CrossRefGoogle Scholar
Spurk, H.J. & Aksel, N. 2008 Fluid Mechanics. Springer.Google Scholar
Stern, M.E. 1975 Minimal properties of planetary eddies. J. Mar. Res. 33, 1–13.Google Scholar
Vallis, G.K. 2017 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Verron, J. & Le Provost, C. 1985 A numerical study of quasi-geostrophic flow over isolated topography. J. Fluid Mech. 154, 231–252.CrossRefGoogle Scholar
Viúdez, A. 2019 a Azimutal mode solutions of two-dimensional Euler flows and the Chaplygin–Lamb dipole. J. Fluid Mech. 859, 1–12.CrossRefGoogle Scholar
Viúdez, A. 2019 b Exact solutions of asymmetric baroclinic quasi-geostrophic dipoles with distributed potential vorticity. J. Fluid Mech. 868, 1–13.CrossRefGoogle Scholar
Watson, G.N. 1986 A Treatise on the Theory of Bessel Functions. Cambridge University Press.Google Scholar
Zavala Sansón, L. 2010 Solutions of barotropic waves around seamounts. J. Fluid Mech. 661, 32–44.CrossRefGoogle Scholar
Zavala Sansón, L., Aguilar, A.B. & van Heijst, G.J.F. 2012 Horizontal and vertical motions of barotropic vortices over a submarine mountain. J. Fluid Mech. 695, 173–198.CrossRefGoogle Scholar
Zavala Sansón, L. & Gonzalez, J.F. 2021 Travelling vortices over mountains and the long-term structure of the residual flow. J. Fluid Mech. (submitted).Google Scholar
Zavala Sansón, L., González-Villanueva, A. & Flores, L.M. 2010 Evolution and decay of a rotating flow over random topography. J. Fluid Mech. 642, 159–180.CrossRefGoogle Scholar
Zavala Sansón, L. & van Heijst, G.J.F. 2014 Laboratory experiments on flows over bottom topography. In Modelling Atmospheric and Oceanics Flows: Insights from Laboratory Experiments and Numerical Simulations (ed. T. von Larcher & P. Williams), pp. 139–158. Wiley.CrossRefGoogle Scholar
Zavala Sansón, L., van Heijst, G.J.F. & Backx, N.A. 2001 Ekman decay of a dipolar vortex in a rotating fluid. Phys. Fluids 13 (2), 440–451.CrossRefGoogle Scholar

Gonzalez and Zavala Sansón supplementary movie 1

Evolution of the relative vorticity of a dipolar vortex on the f-plane over an abrupt mountain (flow parameters in Figure 4a).

Download Gonzalez and Zavala Sansón supplementary movie 1(Video)
Video 614.7 KB

Gonzalez and Zavala Sansón supplementary movie 2

Evolution of the relative vorticity of a dipolar vortex on the f-plane over an abrupt valley (flow parameters in Figure 4c).

Download Gonzalez and Zavala Sansón supplementary movie 2(Video)
Video 719.4 KB