Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T16:39:41.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal heat transfer enhancement in plane Couette flow

Published online by Cambridge University Press:  01 December 2017

Shingo Motoki ,
Genta Kawahara Open the ORCID record for Genta Kawahara [Opens in a new window]  and
Masaki Shimizu
Shingo Motoki
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560–8531, Japan
Genta Kawahara*
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560–8531, Japan
Masaki Shimizu
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560–8531, Japan
*
†Email address for correspondence: kawahara@me.es.osaka-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Optimal heat transfer enhancement has been explored theoretically in plane Couette flow. The vector field (referred to as the ‘velocity’) to be optimised is time independent and divergence free, and temperature is determined in terms of the velocity as a solution to an advection-diffusion equation. The Prandtl number is set to unity, and consistent boundary conditions are imposed on the velocity and the temperature fields. The excess of a wall heat flux (or equivalently total scalar dissipation) over total energy dissipation is taken as an objective functional, and by using a variational method the Euler–Lagrange equations are derived, which are solved numerically to obtain the optimal states in the sense of maximisation of the functional. The laminar conductive field is an optimal state at low Reynolds number 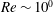$Re\sim 10^{0}$. At higher Reynolds number $Re\sim 10^{1}$, however, the optimal state exhibits a streamwise-independent two-dimensional velocity field. The two-dimensional field consists of large-scale circulation rolls that play a role in heat transfer enhancement with respect to the conductive state as in thermal convection. A further increase of the Reynolds number leads to a three-dimensional optimal state at 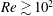$Re\gtrsim 10^{2}$. In the three-dimensional velocity field there appear smaller-scale hierarchical quasi-streamwise vortex tubes near the walls in addition to the large-scale rolls. The streamwise vortices are tilted in the spanwise direction so that they may produce the anticyclonic vorticity antiparallel to the mean-shear vorticity, bringing about significant three-dimensionality. The isotherms wrapped around the tilted anticyclonic vortices undergo the cross-axial shear of the mean flow, so that the spacing of the wrapped isotherms is narrower and so the temperature gradient is steeper than those around a purely streamwise (two-dimensional) vortex tube, intensifying scalar dissipation and so a wall heat flux. Moreover, the tilted anticyclonic vortices induce the flow towards the wall to push low- (or high-) temperature fluids on the hot (or cold) wall, enhancing a wall heat flux. The optimised three-dimensional velocity fields achieve a much higher wall heat flux and much lower energy dissipation than those of plane Couette turbulence.

JFM classification

Flow Control: Mixing enhancement Turbulent Flows: Turbulence control Mathematical Foundations: Variational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 1157 - 1198
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Bodenschatz, E. & He, X. 2014 Logarithmic temperature profiles of turbulent Rayleigh–Bénard convection in the classical and ultimate state for a Prandtl number of 0.8. J. Fluid Mech. 758, 436–467.Google Scholar
Bewley, T. R., Moin, P. & Temam, R. 2001 DNS-based predictive control of turbulence: an optimal benchmark for feedback algorithms. J. Fluid Mech. 447, 179–225.Google Scholar
Busse, F. H. 1969 On Howard’s upper bound for heat transport by turbulent convection. J. Fluid Mech. 37, 457–477.Google Scholar
Busse, F. H. 1970 Bounds for turbulent shear flow. J. Fluid Mech. 41, 219–240.CrossRefGoogle Scholar
Chilton, T. H. & Colburn, A. P. 1934 Mass transfer (absorption) coefficients prediction from data on heat transfer and fluid friction. Ind. Engng Chem. 26, 1183–1187.CrossRefGoogle Scholar
Dipprey, D. F. & Sabersky, R. H. 1963 Heat and momentum transfer in smooth and rough tubes at various Prandtl numbers. J. Heat Mass Transfer 6, 329–353.Google Scholar
Doering, C. R. & Constantin, P. 1992 Energy dissipation in shear driven turbulence. Phys. Rev. Lett. 69, 1648–1651.Google Scholar
Doering, C. R. & Constantin, P. 1994 Variational bounds on energy dissipation in incompressible flows. I. Shear flow. Phys. Rev. E 49 (5), 4087–4099.CrossRefGoogle ScholarPubMed
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53 (6), 5957–5981.Google Scholar
Doering, C. R., Otto, F. & Reznikoff, M. G. 2006 Bounds on vertical heat transport for infinite-Prandtl-number Rayleigh–Bénard convection. J. Fluid Mech. 560, 229–241.CrossRefGoogle Scholar
Hasegawa, Y. & Kasagi, N. 2011 Dissimilar control of momentum and heat transfer in a fully developed turbulent channel flow. J. Fluid Mech. 683, 57–93.CrossRefGoogle Scholar
Hassanzadeh, P., Chini, G. P. & Doering, C. R. 2014 Wall to wall optimal transport. J. Fluid Mech. 751, 627–662.Google Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17, 405–432.Google Scholar
Ierley, G. R., Kerswell, R. R. & Plasting, S. C. 2006 Infinite-Prandtl-number convection. Part 2. A singular limit of upper bound theory. J. Fluid Mech. 560, 159–228.Google Scholar
Kasagi, N., Hasegawa, Y., Fukagata, K. & Iwamoto, K. 2012 Control of turbulent transport less friction and more heat transfer. Trans. ASME J. Heat Transfer 134, 031009.Google Scholar
Kasagi, N., Suzuki, Y. & Fukagata, K. 2009 Microelectromechanical systems-based feedback control of turbulence for skin friction reduction. Annu. Rev. Fluid Mech. 41, 231–251.CrossRefGoogle Scholar
Kawahara, G. 2005 Energy dissipation in spiral vortex layers wrapped around a straight vortex tube. Phys. Fluids 17, 055111.Google Scholar
Kawahara, G., Kida, S., Tanaka, M. & Yanase, S. 1997 Wrap, tilt and stretch of vorticity lines around a strong thin straight vortex tube in a simple shear flow. J. Fluid Mech. 353, 115–162.Google Scholar
Kerswell, R. R. 2001 New results in the variational approach to turbulent Boussinesq convection. Phys. Fluids 13, 192–209.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Moore, D. W. 1985 The interaction of a diffusing line vortex and an aligned shear flow. Proc. R. Soc. Lond. A 399, 367–375.Google Scholar
Nicodemus, R., Grossmann, S. & Holthaus, M. 1997 Improved variational principle for bounds on energy dissipation in turbulent shear flow. Physica D 101, 178–190.Google Scholar
Nicodemus, R., Grossmann, S. & Holthaus, M. 1998a The background flow method. Part 1. Constructive approach to bounds on energy dissipation. J. Fluid Mech. 363, 281–300.CrossRefGoogle Scholar
Nicodemus, R., Grossmann, S. & Holthaus, M. 1998b The background flow method. Part 2. Asymptotic theory of dissipation bounds. J. Fluid Mech. 363, 301–323.Google Scholar
Otero, J., Wittenberg, R. W., Worthing, R. A. & Doering, C. R. 2002 Bounds on Rayleigh–Bénard convection with an imposed heat flux. J. Fluid Mech. 473, 191–199.CrossRefGoogle Scholar
Plasting, S. C. & Kerswell, R. R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solution to Busse’s problem and the Constantin–Doering–Hopf problem with one-dimensional background field. J. Fluid Mech. 477, 363–379.Google Scholar
Reynolds, O. 1874 On the extent and action of the heating surface of steam boilers. Proc. Lit. Phil. Soc. Manchester 14, 7–12.Google Scholar
Robertson, J. M. & Johnson, H. F. 1970 Turbulence structure in plane Couette flow. ASCE J. Engng Mech. Div. Proc. 96, 1171–1182.CrossRefGoogle Scholar
Saad, Y. & Schultz, M. H. 1986 GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7 (3), 856–869.CrossRefGoogle Scholar
Sasamori, M., Mamori, H., Iwamoto, K. & Murata, A. 2014 Experimental study on drag-reduction effect due to sinusoidal riblets in turbulent channel flow. Exp. Fluids 55, 1828.Google Scholar
Sondak, D., Smith, L. M. & Waleffe, F. 2015 Optimal heat transport solutions for Rayleigh–Bénard convection. J. Fluid Mech. 784, 565–595.Google Scholar
Souza, A. N.2016 An optimal control approach to bounding transport properties of thermal convection. PhD thesis, University of Michigan.Google Scholar
Souza, A. N. & Doering, C. R. 2015a Maximal transport in the Lorenz equations. Phys. Lett. A 379, 518–523.Google Scholar
Souza, A. N. & Doering, C. R. 2015b Transport bounds for a truncated model of Rayleigh–Bénard convection. Physica D 308, 26–33.Google Scholar
Suga, K., Mori, M. & Kaneda, M. 2011 Vortex structure of turbulence over permeable walls. Intl J. Heat Fluid Flow 32, 586–595.Google Scholar
Tobasco, I. & Doering, C. R. 2017 Optimal wall-to-wall transport by incompressible flows. Phys. Rev. Lett. 118, 264502.CrossRefGoogle ScholarPubMed
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Viswanath, D. 2009 The critical layer in pipe flow at high Reynolds number. Phil. Trans. R. Soc. Lond. A 367, 561–576.Google Scholar
Whitehead, J. P. & Doering, C. R. 2012 Rigid bounds on heat transport by a fluid between slippery boundaries. J. Fluid Mech. 707, 241–259.Google Scholar
Yamamoto, A., Hasegawa, Y. & Kasagi, N. 2013 Optimal control of dissimilar heat and momentum transfer in a fully developed turbulent channel flow. J. Fluid Mech. 733, 189–220.CrossRefGoogle Scholar