Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T17:43:51.042Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain properties of the compact Zakharov equation

Published online by Cambridge University Press:  07 May 2014

Francesco Fedele
Francesco Fedele*
Affiliation:
School of Civil and Environmental Engineering, School of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, GA, USA
*
†Email address for correspondence: fedele@gatech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Long-time evolution of a weakly perturbed wavetrain near the modulational instability (MI) threshold is examined within the framework of the compact Zakharov equation for unidirectional deep-water waves (Dyachenko and Zakharov, JETP Lett., vol. 93, 2011, pp. 701–705). Multiple-scale solutions reveal that a perturbation to a slightly unstable uniform wavetrain of steepness 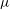$\mu $ slowly evolves according to a nonlinear Schrodinger equation (NLS). In particular, for small carrier wave steepness 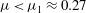$\mu <\mu _{1}\approx 0.27$ the perturbation dynamics is of focusing type and the long-time behaviour is characterized by the Fermi–Pasta–Ulam recurrence, the signature of breather interactions. However, the amplitude of breathers and their likelihood of occurrence tend to diminish as 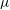$\mu $ increases while the Benjamin–Feir index (BFI) decreases and becomes nil at 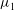$\mu _{1}$. This indicates that homoclinic orbits persist only for small values of wave steepness 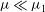$\mu \ll \mu _{1}$, in agreement with recent experimental and numerical observations of breathers. When the compact Zakharov equation is beyond its nominal range of validity, i.e. for 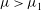$\mu >\mu _{1}$, predictions seem to foreshadow a dynamical trend to wave breaking. In particular, the perturbation dynamics becomes of defocusing type, and nonlinearities tend to stabilize a linearly unstable wavetrain as the Fermi–Pasta–Ulam recurrence is suppressed. At 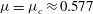$\mu =\mu _{c}\approx 0.577$, subharmonic perturbations restabilize and superharmonic instability appears, possibly indicating that wave dynamical behaviour changes at large steepness, in qualitative agreement with the numerical simulations of Longuet-Higgins and Cokelet (Proc. R. Soc. Lond. A, vol. 364, 1978, pp. 1–28) for steep waves. Indeed, for 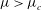$\mu >\mu _{c}$ a multiple-scale perturbation analysis reveals that a weak narrowband perturbation to a uniform wavetrain evolves in accord with a modified Korteweg–de Vries/Camassa–Holm type equation, again implying a possible mechanism conducive to wave breaking.

JFM classification

Instability: Instability Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 692 - 711
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ablowitz, M. J. & Segur, H. 1981 Solitons and the Inverse Scattering Transform. SIAM.CrossRefGoogle Scholar
Baldock, T. E., Swan, C. & Taylor, P. H. 1996 A laboratory study of nonlinear surface waves on water. Phil. Trans. R. Soc. Lond. A 354 (1707), 649–676.Google Scholar
Banner, M. L., Barthelemy, X., Fedele, F., Allis, M., Benetazzo, A., Dias, F. & Peirson, W. L. 2014 Linking reduced breaking crest speeds to unsteady nonlinear water wave group behavior. Phys. Rev. Lett. 112, 114502.CrossRefGoogle ScholarPubMed
Benjamin, T. B. 1967 Instability of periodic wavetrains in nonlinear dispersive systems. Proc. R. Soc. Lond. A 299, 59–75.Google Scholar
Benjamin, T. B. & Feir, J. E. 1967 The disintegration of wavetrains in deep water. Part 1. J. Fluid Mech. 27, 417–430.CrossRefGoogle Scholar
Bridges, T. J. 2004 Superharmonic instability, homoclinic torus bifurcation and water-wave breaking. J. Fluid Mech. 505, 153–162.CrossRefGoogle Scholar
Bridges, T. J. 2013 A universal form for the emergence of the Korteweg–de Vries equation. Proc. R. Soc. Lond. A 469 (2153), 20120707.Google Scholar
Camassa, R. & Holm, D. 1993 An integrable shallow water equation with peaked solitons. Phys. Rev. Lett. 71 (11), 1661–1664.CrossRefGoogle ScholarPubMed
Chabchoub, A., Hoffmann, N. P. & Akhmediev, N. 2011 Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106, 204502.CrossRefGoogle Scholar
Chabchoub, A., Hoffmann, N., Onorato, M. & Akhmediev, N. 2012 Super rogue waves: observation of a higher-order breather in water waves. Phys. Rev. X 2, 011015.Google Scholar
Chu, V. H. & Mei, C. C. 1970 On slowly-varying Stokes waves. J. Fluid Mech. 41, 873–887.CrossRefGoogle Scholar
Clamond, D., Francius, M., Grue, J. & Kharif, C. 2006 Long time interaction of envelope solitons and freak wave formations. Eur. J. Mech. (B/ Fluids) 25 (5), 536–553.CrossRefGoogle Scholar
Crawford, D. R., Lake, B. M., Saffman, P. G. & Yuen, H. C. 1981 Stability of weakly nonlinear deep-water waves in two and three dimensions. J. Fluid Mech. 105, 177–191.CrossRefGoogle Scholar
Dyachenko, A. I., Kachulin, D. I. & Zakharov, V. E. 2013 On the nonintegrability of the free surface hydrodynamics. JETP Lett. 98 (1), 48–52.CrossRefGoogle Scholar
Dyachenko, A. I. & Zakharov, V. E. 2011 Compact equation for gravity waves on deep water. JETP Lett. 93 (12), 701–705.CrossRefGoogle Scholar
Dysthe, K. B. 1979 Note on a modification to the nonlinear Schrödinger equation for application to deep water. Proc. R. Soc. Lond. A 369, 105–114.Google Scholar
Dysthe, K. B., Krogstad, H. E. & Muller, P. 2008 Oceanic rogue waves. Annu. Rev. Fluid Mech. 40, 287–310.CrossRefGoogle Scholar
Dysthe, K. B. & Trulsen, K. 1999 Note on breather type solutions of the NLS as models for freak-waves. Phys. Scr. T82, 48–52.CrossRefGoogle Scholar
Fedele, F., Cherneva, Z., Tayfun, M. A. & Guedes Soares, C. 2010 Nonlinear Schrodinger invariants and wave statistics. Phys. Fluids 22 (3), 036601.CrossRefGoogle Scholar
Fedele, F. & Dutykh, D. 2012 Special solutions to a compact equation for deep-water gravity waves. J. Fluid Mech. 712, 646–660.CrossRefGoogle Scholar
Fermi, E., Pasta, J. & Ulam, H. C.1955 Studies of nonlinear problems, Tech Rep. LA-1940. Los Alamos Scientific Laboratory.CrossRefGoogle Scholar
Gramstad, O. & Trulsen, K. 2007 Influence of crest and group length on the occurrence of freak waves. J. Fluid Mech. 582, 463–472.CrossRefGoogle Scholar
Henderson, K. L., Peregrine, D. H. & Dold, J. W. 1999 Unsteady water wave modulations: fully nonlinear solutions and comparison with the nonlinear Schrödinger equation. Wave Motion 29 (4), 341–361.CrossRefGoogle Scholar
Janssen, P. A. E. M. 1981 Modulational instability and the Fermi–Pasta–Ulam recurrence. Phys. Fluids 24, 23–26.CrossRefGoogle Scholar
Janssen, P. A. E. M. 1983 On a fourth-order envelope equation for deep-water waves. J. Fluid Mech. 126, 1–11.CrossRefGoogle Scholar
Janssen, P. A. E. M. 2003 Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33 (4), 863–884.2.0.CO;2>CrossRefGoogle Scholar
Jillians, W. J. 1989 The superharmonic instability of stokes waves in deep water. J. Fluid Mech. 204, 563–579.CrossRefGoogle Scholar
Kharif, C. & Pelinovsky, E. 2003 Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. (B/ Fluids) 22, 603–634.CrossRefGoogle Scholar
Kharif, C., Pelinovsky, E. & Slunyaev, A. 2009 Rogue Waves in the Ocean. Springer.Google Scholar
Krasitskii, V. P. 1994 On reduced equations in the Hamiltonian theory of weakly nonlinear surface waves. J. Fluid Mech. 272, 1–20.CrossRefGoogle Scholar
Lake, B. M., Yuen, H. C., Rungaldier, H. & Ferguson, W. E. 1977 Nonlinear deep-water waves: theory and experiment. Part 2. Evolution of a continuous wave train. J. Fluid Mech. 83, 49–74.CrossRefGoogle Scholar
Lighthill, M. J. 1965 Contributions to the theory of waves in nonlinear dispersive systems. IMA J. Appl. Maths 1 (3), 269–306.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1978a The instabilities of gravity waves of finite amplitude in deep water. I. Superharmonics. Proc. R. Soc. Lond. A 360 (1703), 471–488.Google Scholar
Longuet-Higgins, M. S. 1978b The instabilities of gravity waves of finite amplitude in deep water II. Subharmonics. Proc. R. Soc. Lond. A 360 (1703), 489–505.Google Scholar
Longuet-Higgins, M. S. & Cokelet, E. D. 1978 The deformation of steep surface waves on water. II. Growth of normal-mode instabilities. Proc. R. Soc. Lond. A 364 (1716), 1–28.Google Scholar
McLean, J. W. 1982 Instabilities of finite-amplitude water waves. J. Fluid Mech. 114, 315–330.CrossRefGoogle Scholar
Mori, N. & Janssen, P. A. E. M. 2006 On kurtosis and occurrence probability of freak waves. J. Phys. Oceanogr. 36 (7), 1471–1483.CrossRefGoogle Scholar
Osborne, A. 2010 Nonlinear Ocean Waves and The Inverse Scattering Transform. vol. 97. Elsevier.Google Scholar
Osborne, A. R., Onorato, M. & Serio, M. 2000 The nonlinear dynamics of rogue waves and holes in deep-water gravity wave trains. Phys. Lett. A 275 (5–6), 386–393.CrossRefGoogle Scholar
Peregrine, D. H. 1983 Water waves, nonlinear Schrödinger equations and their solutions. J. Austral. Math. Soc. B 25, 16–43.CrossRefGoogle Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A 331 (1622), 735–800.Google Scholar
Schober, C. M. 2006 Melnikov analysis and inverse spectral analysis of rogue waves in deep water. Eur. J. Mech. (B/Fluids) 25 (5), 602–620.CrossRefGoogle Scholar
Shemer, L. & Alperovich, S. H. 2013 Peregrine breather revisited. Phys. Fluids 25, 051701.CrossRefGoogle Scholar
Slunyaev, A., Pelinovsky, E., Sergeeva, A., Chabchoub, A., Hoffmann, N., Onorato, M. & Akhmediev, N. 2013 Super-rogue waves in simulations based on weakly nonlinear and fully nonlinear hydrodynamic equations. Phys. Rev. E 88, 012909.CrossRefGoogle ScholarPubMed
Slunyaev, A. V. & Shrira, V. I. 2013 On the highest non-breaking wave in a group: fully nonlinear water wave breathers versus weakly nonlinear theory. J. Fluid Mech. 735, 203–248.CrossRefGoogle Scholar
Sulem, C. & Sulem, P.-L. 1999 The Nonlinear Schrödinger Equation. Self-Focusing and Wave Collapse. Springer.Google Scholar
Tanaka, M. 1990 Maximum amplitude of modulated wavetrain. Wave Motion 12 (6), 559–568.CrossRefGoogle Scholar
Tanaka, M., Dold, J. W., Lewy, M. & Peregrine, D. H. 1987 Instability and breaking of a solitary wave. J. Fluid Mech. 185, 235–248.CrossRefGoogle Scholar
Taniuti, T. & Wei, C.-C. 1968 Reductive perturbation method in nonlinear wave propagation. I. J. Phys. Soc. Japan 24 (4), 941–946.CrossRefGoogle Scholar
Yang, J. 2010 Nonlinear Waves in Integrable and Nonintegrable Systems. SIAM.CrossRefGoogle Scholar
Zakharov, V. E. 1999 Statistical theory of gravity and capillary waves on the surface of a finite-depth fluid. Eur. J. Mech. (B/ Fluids) 18 (3), 327–344.CrossRefGoogle Scholar
Zakharov, V. E. & Shabat, A. B. 1972 Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34, 62–69.Google Scholar