Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-18T06:01:51.782Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical study of a bubble pair rising side by side in external magnetic fields

Published online by Cambridge University Press:  07 September 2021

Jie Zhang Open the ORCID record for Jie Zhang [Opens in a new window]  and
Ming-Jiu Ni Open the ORCID record for Ming-Jiu Ni [Opens in a new window]
Jie Zhang
Affiliation:
State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi'an Jiaotong University, Xi'an, Shaanxi 710049, PR China
Ming-Jiu Ni*
Affiliation:
State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi'an Jiaotong University, Xi'an, Shaanxi 710049, PR China School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China
*
†Email address for correspondence: mjni@ucas.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

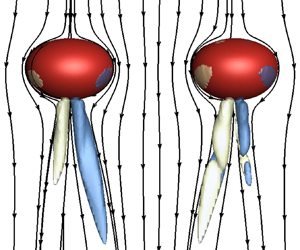
The motion of a pair of bubbles rising side by side under the influence of external magnetic fields is numerically examined. Through solving the fully three-dimensional Navier–Stokes equations, the results reveal that the bubble interactions are rather sensitive to the field direction and strength. At first, we identify that, in a hydrodynamic flow, whether the two bubbles will bounce or coalesce depends on the developments of the counter-rotating streamwise vortices during the collision. In particular, for an originally bouncing bubble pair, a streamwise magnetic field tends to promote their coalescence by weakening the strengths of the standing streamwise vortices, and such a weakening effect is caused by the asymmetric distribution of the Lorentz force in the presence of another bubble such that a torque is induced to offset the original streamwise vortices. Under a horizontal magnetic field, on the other hand, the influences are highly dependent on the angle between the bubble centroid line and the field: a transverse field or a moderate spanwise field always leads the bubble pair to coalescence while a strong spanwise field has the opposite effect. This anisotropic effect comes from the Lorentz force induced flow diffusion along the magnetic field, which not only produces two pairs of streamwise vortices at the bubble rear, but also homogenizes the pressure along the magnetic lines. As the competition between the two mechanisms varies with the magnetic direction and strength, the interaction between the bubble pair also changes. We show that the external magnetic fields control the bubble interaction through reconstructing the vortex structures, and hence the core mechanisms are identified.

JFM classification

Drops and Bubbles: Bubble dynamics MHD and Electrohydrodynamics: Magneto convection Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 926 , 10 November 2021 , A22
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adoua, R., Legendre, D. & Magnaudet, J. 2009 Reversal of the lift force on an oblate bubble in a weakly viscous linear shear flow. J. Fluid Mech. 628, 23–41.CrossRefGoogle Scholar
Bunner, B. & Tryggvason, G. 2002 Dynamics of homogeneous bubbly flows Part 2. Velocity fluctuations. J. Fluid Mech. 466, 53–84.CrossRefGoogle Scholar
Cano-Lozano, J.C., Martinez-Bazan, C., Magnaudet, J. & Tchoufag, J. 2016 Paths and wakes of deformable nearly spheroidal rising bubbles close to the transition to path instability. Phys. Rev. Fluids 1 (5), 053604.CrossRefGoogle Scholar
Davidson, P.A. 1995 Magnetic damping of jets and vortices. J. Fluid Mech. 299, 153–186.CrossRefGoogle Scholar
Delacroix, J. & Davoust, L. 2018 Drag upon a sphere suspended in a low magnetic-Reynolds number MHD channel flow. Phys. Rev. Fluids 3 (12), 123701.CrossRefGoogle Scholar
Duineveld, P.C. 1998 Bouncing and coalescence of bubble pairs rising at high Reynolds number in pure water or aqueous surfactant solutions. In Applied Scientific Research (ed. A. Biesheuvel & G.J.F. van Heijst), pp. 409–439. Springer.CrossRefGoogle Scholar
Eckert, S., Gerbeth, G. & Lielausis, O. 2000 a The behaviour of gas bubbles in a turbulent liquid metal magnetohydrodynamic flow: Part I: dispersion in quasi-two-dimensional magnetohydrodynamic turbulence. Intl J. Multiphase Flow 26 (1), 45–66.CrossRefGoogle Scholar
Eckert, S., Gerbeth, G. & Lielausis, O. 2000 b The behaviour of gas bubbles in a turbulent liquid metal magnetohydrodynamic flow: Part II: magnetic field influence on the slip ratio. Intl J. Multiphase Flow 26 (1), 67–82.CrossRefGoogle Scholar
Gherson, P. & Lykoudis, P.S. 1984 Local measurements in two-phase liquid-metal magneto-fluid-mechanic flow. J. Fluid Mech. 147, 81–104.CrossRefGoogle Scholar
Hallez, Y. & Legendre, D. 2011 Interaction between two spherical bubbles rising in a viscous liquid. J. Fluid Mech. 673, 406–431.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jin, K., Kumar, P., Vanka, S.P. & Thomas, B.G. 2016 Rise of an argon bubble in liquid steel in the presence of a transverse magnetic field. Phys. Fluids 28 (9), 093301.CrossRefGoogle Scholar
Keplinger, O., Shevchenko, N. & Eckert, S. 2019 Experimental investigations of bubble chains in a liquid metal under the influence of a horizontal magnetic field. Intl J. Multiphase Flow 121, 103111.CrossRefGoogle Scholar
Kong, G., Mirsandi, H., Buist, K.A., Peters, E.A.J.F., Baltussen, M.W. & Kuipers, J.A.M. 2019 Hydrodynamic interaction of bubbles rising side-by-side in viscous liquids. Exp. Fluids 60 (10), 155.CrossRefGoogle Scholar
Krasnov, D., Rossi, M., Zikanov, O. & Boeck, T. 2008 a Optimal growth and transition to turbulence in channel flow with spanwise magnetic field. J. Fluid Mech. 596, 73–101.CrossRefGoogle Scholar
Krasnov, D., Zikanov, O., Schumacher, J. & Boeck, T. 2008 b Magnetohydrodynamic turbulence in a channel with spanwise magnetic field. Phys. Fluids 20 (9), 095105.CrossRefGoogle Scholar
Kusuno, H., Yamamoto, H. & Sanada, T. 2019 Lift force acting on a pair of clean bubbles rising in-line. Phys. Fluids 31 (7), 072105.CrossRefGoogle Scholar
Lammers, J.H. & Biesheuvel, A. 1996 Concentration waves and the instability of bubbly flows. J. Fluid Mech. 328, 67–93.CrossRefGoogle Scholar
Legendre, D., Magnaudet, J. & Mougin, G. 2003 Hydrodynamic interactions between two spherical bubbles rising side by side in a viscous liquid. J. Fluid Mech. 497, 133–166.CrossRefGoogle Scholar
Loisy, A., Naso, A. & Spelt, P. 2017 Buoyancy-driven bubbly flows: ordered and free rise at small and intermediate volume fraction. J. Fluid Mech. 816, 94–141.CrossRefGoogle Scholar
Magnaudet, J. & Mougin, G. 2007 Wake instability of a fixed spheroidal bubble. J. Fluid Mech. 572, 311–337.CrossRefGoogle Scholar
Miao, X., Lucas, D., Ren, Z., Eckert, S. & Gerbeth, G. 2013 Numerical modeling of bubble-driven liquid metal flows with external static magnetic field. Intl J. Multiphase Flow 48, 32–45.CrossRefGoogle Scholar
Michiyoshi, I. 1989 Liquid metal two-phase flow heat transfer with and without magnetic field. JSME Intl J. 32 (4), 483–493.Google Scholar
Mirsandi, H., Baltussen, M.W., Peters, E.A.J.F., van Odyck, D.E.A., van Oord, J., van der Plas, D. & Kuipers, J.A.M. 2020 Numerical simulations of bubble formation in liquid metal. Intl J. Multiphase Flow 131, 103363.CrossRefGoogle Scholar
Ni, M.-J., Munipalli, R., Morley, N.B., Huang, P. & Abdou, M.A. 2007 A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part I: on a rectangular collocated grid system. J. Comput. Phys. 227 (1), 174–204.CrossRefGoogle Scholar
Pan, J.-H., Zhang, N.-M. & Ni, M.-J. 2018 The wake structure and transition process of a flow past a sphere affected by a streamwise magnetic field. J. Fluid Mech. 842, 248–272.CrossRefGoogle Scholar
Pan, J.-H., Zhang, N.-M. & Ni, M.-J. 2019 Wake structure of laminar flow past a sphere under the influence of a transverse magnetic field. J. Fluid Mech. 873, 151–173.CrossRefGoogle Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.CrossRefGoogle Scholar
Richter, T., Keplinger, O., Shevchenko, N., Wondrak, T., Eckert, K., Eckert, S. & Odenbach, S. 2018 Single bubble rise in GaInSn in a horizontal magnetic field. Intl J. Multiphase Flow 104, 32–41.CrossRefGoogle Scholar
Sanada, T., Sato, A., Shirota, M. & Watanabe, M. 2009 Motion and coalescence of a pair of bubbles rising side by side. Chem. Engng Sci. 64 (11), 2659–2671.CrossRefGoogle Scholar
Sangani, A.S. & Didwania, A.K. 1993 Dynamic simulations of flows of bubbly liquids at large Reynolds numbers. J. Fluid Mech. 250, 307–337.CrossRefGoogle Scholar
Schwarz, S. & Fröhlich, J. 2014 Numerical study of single bubble motion in liquid metal exposed to a longitudinal magnetic field. Intl J. Multiphase Flow 62, 134–151.CrossRefGoogle Scholar
Smereka, P. 1993 On the motion of bubbles in a periodic box. J. Fluid Mech. 254, 79–112.CrossRefGoogle Scholar
Sommeria, J. & Moreau, R. 1982 Why, how, and when, MHD turbulence becomes two-dimensional J. Fluid Mech. 118, 507–518.CrossRefGoogle Scholar
Tripathi, M.K., Premlata, A.R., Sahu, K.C. & Govindarajan, R. 2017 Two initially spherical bubbles rising in quiescent liquid. Phys. Rev. Fluids 2 (7), 073601.CrossRefGoogle Scholar
Tripathi, M.K., Sahu, K.C. & Govindarajan, R. 2015 Dynamics of an initially spherical bubble rising in quiescent liquid. Nat. Commun. 6, 6268.CrossRefGoogle ScholarPubMed
Wang, Z.H., Wang, S.D., Meng, X. & Ni, M.J. 2017 UDV measurements of single bubble rising in a liquid metal Galinstan with a transverse magnetic field. Intl J. Multiphase Flow 94, 201–208.CrossRefGoogle Scholar
Wiederhold, A., Boeck, T. & Resagk, C. 2017 Detection and characterization of elongated bubbles and drops in two-phase flow using magnetic fields. Meas. Sci. Technol. 28 (8), 085303.CrossRefGoogle Scholar
Zhang, C. 2009 Liquid metal flows drive by gas bubbles in a static magnetic field. PhD thesis, Department of Magnetohydrodynamics, Forschungszentrum Dresden-Rossendorf.Google Scholar
Zhang, C., Eckert, S. & Berbeth, G. 2007 The flow structure of a bubble-driven liquid-metal jet in a horizontal magnetic field. J. Fluid Mech. 575, 57–82.CrossRefGoogle Scholar
Zhang, C., Eckert, S. & Gerbeth, G. 2005 Experimental study of single bubble motion in a liquid metal column exposed to a DC magnetic field. Intl J. Multiphase Flow 31 (7), 824–842.CrossRefGoogle Scholar
Zhang, J., Chen, L. & Ni, M.-J. 2019 Vortex interactions between a pair of bubbles rising side by side in ordinary viscous liquids. Phys. Rev. Fluids 4 (4), 043604.CrossRefGoogle Scholar
Zhang, J. & Ni, M.-J. 2014 a Direct simulation of multi-phase MHD flows on an unstructured Cartesian adaptive system. J. Comput. Phys. 270, 345–365.CrossRefGoogle Scholar
Zhang, J. & Ni, M.-J. 2014 b Direct simulation of single bubble motion under vertical magnetic field: paths and wakes. Phys. Fluids (1994-present) 26 (10), 102102.CrossRefGoogle Scholar
Zhang, J. & Ni, M.-J. 2017 What happens to the vortex structures when the rising bubble transits from zigzag to spiral? J. Fluid Mech. 828, 353–373.CrossRefGoogle Scholar
Zhang, J., Ni, M.-J. & Moreau, R. 2016 Rising motion of a single bubble through a liquid metal in the presence of a horizontal magnetic field. Phys. Fluids 28 (3), 032101.CrossRefGoogle Scholar
Supplementary material: File

Zhang and Ni supplementary material

Zhang and Ni supplementary material

Download Zhang and Ni supplementary material(File)
File 54.2 MB