Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T09:54:00.438Z Has data issue: false hasContentIssue false
  • English
  • Français

New exotic capillary free-surface flows

Published online by Cambridge University Press:  29 July 2020

A. Doak Open the ORCID record for A. Doak [Opens in a new window]  and
J.-M. Vanden-Broeck
A. Doak*
Affiliation:
Department of Mathematical Sciences, Univesity of Bath, BathBA2 7AY, UK
J.-M. Vanden-Broeck
Affiliation:
Department of Mathematics, University College London, LondonWC1E 6BT, UK
*
†Email address for correspondence: add49@bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

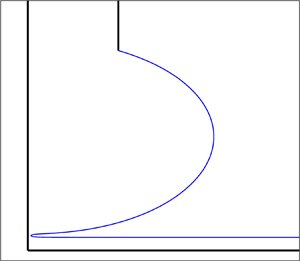
In this paper, we consider two-dimensional steady free-surface flows where gravity is ignored, but the effects of surface tension are included. It is found that the existence of an additional solid boundary can allow for previously unseen limiting configurations as the surface tension tends to infinity. The free surface of these new solutions is formed of straight lines, arcs of circles and a point where the flow turns at a wall. These limiting configurations form endpoints of solution branches of capillary free-surface flows. Other endpoints of these branches include the surface tension free (i.e. free streamline) solution, and a solution whose free surface is composed simply of a straight line. The model we explore is flow incoming along a channel of constant width. One of the walls terminates, where the fluid is forcibly separated from the wall and a free boundary is formed. The other wall meets a second straight boundary with interior angle $\beta$. Far downstream the solution approaches a uniform stream. Making use of Cauchy's integral formula, the unknowns are expressed in terms of values on the boundary. The integral equations are then solved numerically. The solution space relative to the parameter values of the model is discussed.

JFM classification

Interfacial Flows (free surface): Capillary flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 899 , 25 September 2020 , R4
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ackerberg, R. C. 1975 The effects of capillarity on free-streamline separation. J. Fluid Mech. 70 (2), 333–352.CrossRefGoogle Scholar
Birkhoff, G. & Carter, D. 1957 Rising plane bubbles. J. Math. Mech. 6 (4), 769–779.Google Scholar
Chandler, T. G. J. & Trinh, P. H. 2018 Complex singularities near the intersection of a free surface and wall. Part 1. Vertical jets and rising bubbles. J. Fluid Mech. 856, 323–350.CrossRefGoogle Scholar
Christodoulides, P. & Dias, F. 2010 Impact of a falling jet. J. Fluid Mech. 657, 22–35.CrossRefGoogle Scholar
Couët, B. & Strumolo, G. S. 1987 The effects of surface tension and tube inclination on a two-dimensional rising bubble. J. Fluid Mech. 184, 1–14.CrossRefGoogle Scholar
Crapper, G. D. 1957 An exact solution for progressive capillary waves of arbitrary amplitude. J. Fluid Mech. 2 (6), 532–540.CrossRefGoogle Scholar
Cumberbatch, E. & Norbury, J. 1979 Capillary modification of the singularity at a free-streamline separation point. Q. J. Mech. Appl. Maths 32 (3), 303–312.CrossRefGoogle Scholar
Daripa, P. 2000 The fastest smooth Taylor bubble. Appl. Numer. Maths 34 (4), 373–379.CrossRefGoogle Scholar
Doak, A. & Vanden-Broeck, J.-M. 2020 Nonlinear two-dimensional free surface solutions of flow exiting a pipe and impacting a wedge. J. Engng Maths (submitted).Google Scholar
Garabedian, P. R. 1957 On steady-state bubbles generated by Taylor instability. Proc. R. Soc. Lond. A 241 (1226), 423–431.Google Scholar
Hocking, G. C. & Forbes, L. K. 2010 Steady flow of a buoyant plume into a constant-density layer. J. Engng Maths 67 (4), 341–350.CrossRefGoogle Scholar
Kinnersley, W. 1976 Exact large amplitude capillary waves on sheets of fluid. J. Fluid Mech. 77 (2), 229–241.CrossRefGoogle Scholar
Love, A. E. H. 1891 On the Theory of Discontinuous Fluid Motions in Two Dimensions. Cambridge Philosophical Society.Google Scholar
Modi, V. 1985 Comment on “Bubbles rising in a tube and jets falling from a nozzle”. Phys. Fluids 28 (11), 3432–3433.CrossRefGoogle Scholar
Tooley, S. & Vanden-Broeck, J.-M. 2002 Waves and singularities in nonlinear capillary free-surface flows. J. Engng Maths 43 (1), 89–99.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1981 The influence of capillarity on cavitating flow past a flat plate. Q. J. Mech. Appl. Maths 34 (4), 465–473.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1983 The influence of surface tension on cavitating flow past a curved obstacle. J. Fluid Mech. 133, 255–264.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1984 a The effect of surface tension on the shape of the Kirchhoff jet. Phys. Fluids 27 (8), 1933–1936.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1984 b Bubbles rising in a tube and jets falling from a nozzle. Phys. Fluids 27 (5), 1090–1093.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1984 c Rising bubbles in a two-dimensional tube with surface tension. Phys. Fluids 27 (11), 2604–2607.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 1986 Pointed bubbles rising in a two-dimensional tube. Phys. Fluids 29, 1343–1344.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2004 Nonlinear capillary free-surface flows. J. Engng Maths 50 (4), 415–426.CrossRefGoogle Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.CrossRefGoogle Scholar