1 Introduction
The Richtmyer–Meshkov (RM) instability (Richtmyer Reference Richtmyer1960; Meshkov Reference Meshkov1969) occurs when an arbitrarily perturbed interface separating two different fluids is impulsively accelerated by a shock wave. It shares similarities with the Rayleigh–Taylor (RT) instability (Rayleigh Reference Rayleigh1883; Taylor Reference Taylor1950) where initial perturbations at the interface grow and eventually evolve into a turbulent flow field through the transfer of potential to kinetic energy when the interface experiences a constant acceleration pointing from the lighter fluid to the heavier one. RM and RT instabilities play a central role in the performance degradation of spherical implosions in inertial confinement fusion (Lindl et al.
Reference Lindl, Landen, Edwards, Moses and Team2014). The perturbation in RM instability is always unstable regardless of the shock direction, while the RT effect may be unstable or stable depending on whether the acceleration is directed from the lighter fluid to the heavier one or vice versa. The RM instability is mainly governed by the production of baroclinic vorticity (
![]() $\unicode[STIX]{x1D714}$
) which results from the misalignment of the pressure gradient (
$\unicode[STIX]{x1D714}$
) which results from the misalignment of the pressure gradient (
![]() $\unicode[STIX]{x1D735}p$
) associated with the shock wave and the density gradient (
$\unicode[STIX]{x1D735}p$
) associated with the shock wave and the density gradient (
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
) of the material interface:
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}$
) of the material interface:
![]() $D\unicode[STIX]{x1D714}/Dt=(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D735}p)/\unicode[STIX]{x1D70C}^{2}$
. The perturbations grow linearly until their amplitudes become comparable to their wavelengths. Eventually, the interface develops into a turbulent mixing layer (Mohaghar et al.
Reference Mohaghar, Carter, Musci, Reilly, McFarland and Ranjan2017; Zhou Reference Zhou2017). The RM instability has become increasingly significant in many areas of scientific research such as inertial confinement fusion (ICF) (Lindl et al.
Reference Lindl, Landen, Edwards, Moses and Team2014), supersonic combustion (Yang, Kubota & Zukoski Reference Yang, Kubota and Zukoski1993) and astrophysical problems (Arnett et al.
Reference Arnett, Bahcall, Kirshner and Woosley1989), and several comprehensive reviews on the RM instability have been made (Zabusky Reference Zabusky1999; Brouillette Reference Brouillette2002; Ranjan, Oakley & Bonazza Reference Ranjan, Oakley and Bonazza2011; Luo et al.
Reference Luo, Zhai, Si and Yang2014b
).
$D\unicode[STIX]{x1D714}/Dt=(\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}\times \unicode[STIX]{x1D735}p)/\unicode[STIX]{x1D70C}^{2}$
. The perturbations grow linearly until their amplitudes become comparable to their wavelengths. Eventually, the interface develops into a turbulent mixing layer (Mohaghar et al.
Reference Mohaghar, Carter, Musci, Reilly, McFarland and Ranjan2017; Zhou Reference Zhou2017). The RM instability has become increasingly significant in many areas of scientific research such as inertial confinement fusion (ICF) (Lindl et al.
Reference Lindl, Landen, Edwards, Moses and Team2014), supersonic combustion (Yang, Kubota & Zukoski Reference Yang, Kubota and Zukoski1993) and astrophysical problems (Arnett et al.
Reference Arnett, Bahcall, Kirshner and Woosley1989), and several comprehensive reviews on the RM instability have been made (Zabusky Reference Zabusky1999; Brouillette Reference Brouillette2002; Ranjan, Oakley & Bonazza Reference Ranjan, Oakley and Bonazza2011; Luo et al.
Reference Luo, Zhai, Si and Yang2014b
).
During the past few decades, the interaction of a planar shock wave with a two-dimensional (2-D) single-mode interface was discussed extensively. The 2-D incompressible impulsive model proposed by Richtmyer (Reference Richtmyer1960) was verified to be applicable in the light/heavy configuration at the early linear stage (Collins & Jacobs Reference Collins and Jacobs2002). More accurately, the compressible linear model has been proposed by Wouchuk (Reference Wouchuk2001a ,Reference Wouchuk b ), considering the ripples around the interface when a shock or refraction wave is reflected. When the amplitude-to-wavelength ratio approaches one, the perturbation growth goes through a nonlinear process, showing a distinct discrepancy from the linear prediction (Rikanati et al. Reference Rikanati, Oron, Sadot and Shvarts2003). Many theoretical and empirical models were developed to predict the nonlinear growth and the following turbulent mixing, and a relatively exhaustive review has been conducted by Abarzhi (Reference Abarzhi2008). In recent years, the planar RM instability induced by strong shocks has also attracted much attention (Dell, Stellingwerf & Abarzhi Reference Dell, Stellingwerf and Abarzhi2015).
Compared with the planar RM instability, the converging RM instability is more closely related to the reality of ICF. In the converging RM instability, both the radial (r) and the angular (
![]() $\unicode[STIX]{x1D703}$
) directions are involved. Bell (Reference Bell1951) and Plesset (Reference Plesset1954) firstly analysed the early time growth of the RT instability in cylindrical and spherical geometries, and found that the growth rate of perturbations varies with the radius of the interface, which is later called the Bell–Plesset (BP) effect. Several nonlinear models (Mikaelian Reference Mikaelian2005; Matsuoka & Nishihara Reference Matsuoka and Nishihara2006; Liu, He & Yu Reference Liu, He and Yu2012; Liu et al.
Reference Liu, Yu, Ye, Wang and He2014; Wang et al.
Reference Wang, Wu, Guo, Ye, Liu, Zhang and He2015) revealed that the BP effect suppresses the nonlinearity and extends the linear stage longer than that in the planar configuration, as demonstrated in a laser driven experiment (Fincke et al.
Reference Fincke, Lanier, Batha, Hueckstaedt, Magelssen, Rothman, Parker and Horsfield2005). Besides, for the continuously radial flow after the converging shock, the interface as a whole is in a non-uniform pressure field, which inevitably introduces the RT effect. The RT effect in the converging RM instability has been reported in experiments on the OMEGA laser (Lanier et al.
Reference Lanier, Barnes, Batha, Day, Magelssen, Scott, Dunne, Parker and Rothman2003) and in numerical simulations (Lombardini, Pullin & Meiron Reference Lombardini, Pullin and Meiron2014). Therefore, the coupling of BP effect, RT effect and multiple impacts (shock reflects back and forth between the interface and the convergence centre) greatly increases the complexity of the converging RM instability. In previous work (Meshkov, Nevmerzhitsky & Zmushko Reference Meshkov, Nevmerzhitsky and Zmushko1997a
; Meshkov, Nikiforov & Tolshmyakov Reference Meshkov, Nikiforov and Tolshmyakov1997b
), investigations on turbulent mixing development in spherical and cylindrical geometries were attempted, and the interface mixing width as well as the RT effect were simply analysed. However, the initially convergent shock wave was disturbed, and only limited data were extracted from the experiments. Kumar, Hornung & Sturtevant (Reference Kumar, Hornung and Sturtevant2003) studied the growth of a multi-mode initial interface, formed by sandwiching a polymeric membrane between wire-mesh frames, in a conical geometry, and found that the turbulent mixing zone at very late time has a relatively larger growth rate than the planar counterpart. These studies focused on the turbulent mixing stage, and a direct experimental observation of the very complex process of the converging RM instability is still desirable.
$\unicode[STIX]{x1D703}$
) directions are involved. Bell (Reference Bell1951) and Plesset (Reference Plesset1954) firstly analysed the early time growth of the RT instability in cylindrical and spherical geometries, and found that the growth rate of perturbations varies with the radius of the interface, which is later called the Bell–Plesset (BP) effect. Several nonlinear models (Mikaelian Reference Mikaelian2005; Matsuoka & Nishihara Reference Matsuoka and Nishihara2006; Liu, He & Yu Reference Liu, He and Yu2012; Liu et al.
Reference Liu, Yu, Ye, Wang and He2014; Wang et al.
Reference Wang, Wu, Guo, Ye, Liu, Zhang and He2015) revealed that the BP effect suppresses the nonlinearity and extends the linear stage longer than that in the planar configuration, as demonstrated in a laser driven experiment (Fincke et al.
Reference Fincke, Lanier, Batha, Hueckstaedt, Magelssen, Rothman, Parker and Horsfield2005). Besides, for the continuously radial flow after the converging shock, the interface as a whole is in a non-uniform pressure field, which inevitably introduces the RT effect. The RT effect in the converging RM instability has been reported in experiments on the OMEGA laser (Lanier et al.
Reference Lanier, Barnes, Batha, Day, Magelssen, Scott, Dunne, Parker and Rothman2003) and in numerical simulations (Lombardini, Pullin & Meiron Reference Lombardini, Pullin and Meiron2014). Therefore, the coupling of BP effect, RT effect and multiple impacts (shock reflects back and forth between the interface and the convergence centre) greatly increases the complexity of the converging RM instability. In previous work (Meshkov, Nevmerzhitsky & Zmushko Reference Meshkov, Nevmerzhitsky and Zmushko1997a
; Meshkov, Nikiforov & Tolshmyakov Reference Meshkov, Nikiforov and Tolshmyakov1997b
), investigations on turbulent mixing development in spherical and cylindrical geometries were attempted, and the interface mixing width as well as the RT effect were simply analysed. However, the initially convergent shock wave was disturbed, and only limited data were extracted from the experiments. Kumar, Hornung & Sturtevant (Reference Kumar, Hornung and Sturtevant2003) studied the growth of a multi-mode initial interface, formed by sandwiching a polymeric membrane between wire-mesh frames, in a conical geometry, and found that the turbulent mixing zone at very late time has a relatively larger growth rate than the planar counterpart. These studies focused on the turbulent mixing stage, and a direct experimental observation of the very complex process of the converging RM instability is still desirable.
The converging RM instability has rarely been studied in a shock tube circumstance mainly due to the difficulty of generating a stable converging shock in laboratory conditions. There are only few works on the cylindrically converging shock (Perry & Kantrowitz Reference Perry and Kantrowitz1951; Takayama, Kleine & Grönig Reference Takayama, Kleine and Grönig1987; Dimotakis & Samtaney Reference Dimotakis and Samtaney2006; Zhai et al.
Reference Zhai, Liu, Qin, Yang and Luo2010; Luo et al.
Reference Luo, Ding, Wang, Zhai and Si2015) and, consequently, shock tube experiments on the converging RM instability are scarce (Hosseini & Takayama Reference Hosseini and Takayama2005; Si, Zhai & Luo Reference Si, Zhai and Luo2014; Biamino et al.
Reference Biamino, Jourdan, Mariani, Houas, Vandenboomgaerde and Souffland2015; Si et al.
Reference Si, Long, Zhai and Luo2015). Recently, two quantitative shock tube experiments were, respectively, reported in a semi-annular converging shock tube (Ding et al.
Reference Ding, Si, Yang, Lu, Zhai and Luo2017) and a coaxial converging shock tube (Lei et al.
Reference Lei, Ding, Si, Zhai and Luo2017), in which a reduction of growth rate was found and was ascribed to the RT stabilization effect caused by the interface deceleration motion existing in the converging circumstance. However, these shock tubes have a very short test length (
![]() $R_{T}\leqslant 50$
mm) such that only few data points were acquired and the BP effect is significant. As a result, the effective time of the RT stabilization effect was limited (less than
$R_{T}\leqslant 50$
mm) such that only few data points were acquired and the BP effect is significant. As a result, the effective time of the RT stabilization effect was limited (less than
![]() $70~\unicode[STIX]{x03BC}$
s), and the intensive coupling of the BP and RT effects made the analysis difficult. Therefore, more experiments on the single-mode interface are needed to explore physical mechanisms in the converging RM instability in a relatively long time scale.
$70~\unicode[STIX]{x03BC}$
s), and the intensive coupling of the BP and RT effects made the analysis difficult. Therefore, more experiments on the single-mode interface are needed to explore physical mechanisms in the converging RM instability in a relatively long time scale.
2 Experimental method
In this work, the converging RM instability is quantitatively studied in a cylindrically converging shock tube which has already verified its feasibility and reliability for the studies of the converging RM instability in our previous work (Luo et al.
Reference Luo, Si, Yang and Zhai2014a
; Si et al.
Reference Si, Zhai and Luo2014) and, therefore, only a brief description of this facility is given here. This shock tube consists of a 1.7 m driver section, a 2.0 m driven section and a 1.2 m test section. The incident planar shock Mach number is
![]() $M_{s}=1.2$
and the cross-sectional area is 140 mm
$M_{s}=1.2$
and the cross-sectional area is 140 mm
![]() $\times$
20 mm. Both the driver and driven gases are air. As sketched in figure 1(a), the converging section for testing is very slender (radial length
$\times$
20 mm. Both the driver and driven gases are air. As sketched in figure 1(a), the converging section for testing is very slender (radial length
![]() $R_{T}=$
212 mm, with a convergent angle of
$R_{T}=$
212 mm, with a convergent angle of
![]() $15^{\circ }$
and a height of 140 mm) so that the physical mechanisms in the converging RM instability can be amply exhibited for a sufficiently long time scale. The soap film technique is used to generate the discontinuous gaseous interface in the converging shock tube. As shown in figure 1(b), the interface generation device consists of several acrylic sheets (fixed A and C, moveable B2, supplementary B1 and B3 pasted on C) and two sinusoidal wires embedded on A and B2. Before each experiment run, liquid soap (made of 78 % distilled water, 2 % sodium oleate and 20 % glycerine by mass) is injected from holes in A into the sinusoidal wires and then the interface is generated by pulling B2 down to C. As indicated in figure 1(c), these two sinusoidal channels are perpendicular to the edges, keeping symmetric on the edge for its consistency with completely cylindrical shock experiments. To guarantee a stable generation of the interface, the two sinusoidal wires are both 1 mm beyond the acrylic sheets, thus the effective height of the interface is
$15^{\circ }$
and a height of 140 mm) so that the physical mechanisms in the converging RM instability can be amply exhibited for a sufficiently long time scale. The soap film technique is used to generate the discontinuous gaseous interface in the converging shock tube. As shown in figure 1(b), the interface generation device consists of several acrylic sheets (fixed A and C, moveable B2, supplementary B1 and B3 pasted on C) and two sinusoidal wires embedded on A and B2. Before each experiment run, liquid soap (made of 78 % distilled water, 2 % sodium oleate and 20 % glycerine by mass) is injected from holes in A into the sinusoidal wires and then the interface is generated by pulling B2 down to C. As indicated in figure 1(c), these two sinusoidal channels are perpendicular to the edges, keeping symmetric on the edge for its consistency with completely cylindrical shock experiments. To guarantee a stable generation of the interface, the two sinusoidal wires are both 1 mm beyond the acrylic sheets, thus the effective height of the interface is
![]() $d_{0}=18$
mm. The initial interface position is set as
$d_{0}=18$
mm. The initial interface position is set as
![]() $R_{0}=195$
mm, and the incident shock Mach number is 1.26 at
$R_{0}=195$
mm, and the incident shock Mach number is 1.26 at
![]() $R_{0}=195$
mm. In order to generate an air/
$R_{0}=195$
mm. In order to generate an air/
![]() $\text{SF}_{6}$
interface, as shown in figure 2(a), an inflow conduit is inserted from the side wall to fill
$\text{SF}_{6}$
interface, as shown in figure 2(a), an inflow conduit is inserted from the side wall to fill
![]() $\text{SF}_{6}$
into the test section. The original air is exhausted from the outflow hole, and a sealpad is placed behind the interface to prevent
$\text{SF}_{6}$
into the test section. The original air is exhausted from the outflow hole, and a sealpad is placed behind the interface to prevent
![]() $\text{SF}_{6}$
spreading to the former planar section. When the
$\text{SF}_{6}$
spreading to the former planar section. When the
![]() $\text{SF}_{6}$
at the outflow hole has been detected by a gas concentration detector to be pure enough, the interface is quickly generated, followed by the block of the inflow hole and the pumping out of the residual
$\text{SF}_{6}$
at the outflow hole has been detected by a gas concentration detector to be pure enough, the interface is quickly generated, followed by the block of the inflow hole and the pumping out of the residual
![]() $\text{SF}_{6}$
between the interface and sealpad. Subsequently, the sealpad is quickly taken out and an air/
$\text{SF}_{6}$
between the interface and sealpad. Subsequently, the sealpad is quickly taken out and an air/
![]() $\text{SF}_{6}$
interface is formed. It is well known that the initial conditions are crucial for development of the RM instability. During the generation of the initial interface, both sides of the interface are connected to keep the pressures at both sides of interface in balance. When the interface is formed, there might be a little bit difference in pressure just based on how one closes the valve. However, this difference (
$\text{SF}_{6}$
interface is formed. It is well known that the initial conditions are crucial for development of the RM instability. During the generation of the initial interface, both sides of the interface are connected to keep the pressures at both sides of interface in balance. When the interface is formed, there might be a little bit difference in pressure just based on how one closes the valve. However, this difference (
![]() ${\sim}$
several Pa) is so small that it can be ignored. Moreover, after the interface formation and before the experiment start, the time interval allows for the diffusion of gases at both sides, and the pressures tended to be more stable. As a result, the shape of the interface with the minimum surface feature is unchanged as long as the experimental apparatus is kept. Of course, the gas concentration cannot be guaranteed to be the same for each experimental run. However, the differences among the experimental runs are not significant, and the slight diversity of the gas concentration will not greatly affect the interface morphology and perturbation growth.
${\sim}$
several Pa) is so small that it can be ignored. Moreover, after the interface formation and before the experiment start, the time interval allows for the diffusion of gases at both sides, and the pressures tended to be more stable. As a result, the shape of the interface with the minimum surface feature is unchanged as long as the experimental apparatus is kept. Of course, the gas concentration cannot be guaranteed to be the same for each experimental run. However, the differences among the experimental runs are not significant, and the slight diversity of the gas concentration will not greatly affect the interface morphology and perturbation growth.
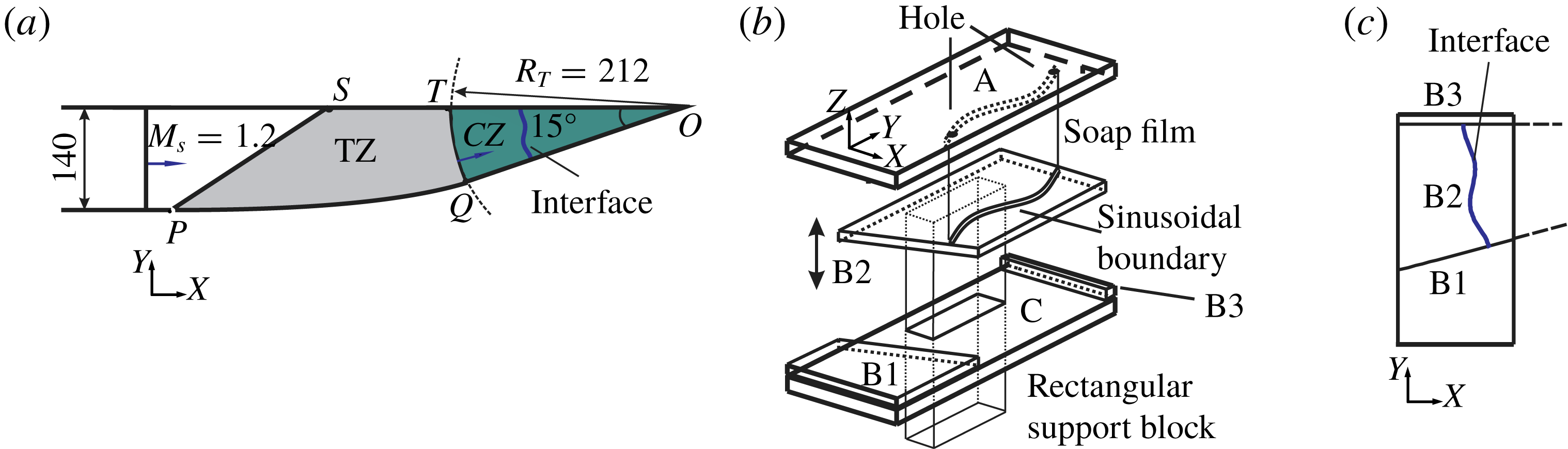
Figure 1. Schematics of the test section of the converging shock tube (a), the device to generate soap film interface (b) and the interface location on the lower window (consisting of three acrylic sheets: B1, B2 and B3 (c). CZ: convergent zone, TZ: transition zone. Numbers are in mm except the Mach number.
A Z-fold schlieren system is adopted to visualize the flow field through two observation windows mounted in the test section, as sketched in figure 2(a). Illuminated by a mercury lamp light source, the flow field is captured by a high-speed video camera (FASTCAM SA5, Photron Limited) with the shutter at
![]() $1~\unicode[STIX]{x03BC}$
s. The temporal and spatial resolutions respectively are
$1~\unicode[STIX]{x03BC}$
s. The temporal and spatial resolutions respectively are
![]() $20~\unicode[STIX]{x03BC}\text{s}~\text{frame}^{-1}$
and
$20~\unicode[STIX]{x03BC}\text{s}~\text{frame}^{-1}$
and
![]() ${\sim}0.29~\text{mm}~\text{pixel}^{-1}$
.
${\sim}0.29~\text{mm}~\text{pixel}^{-1}$
.
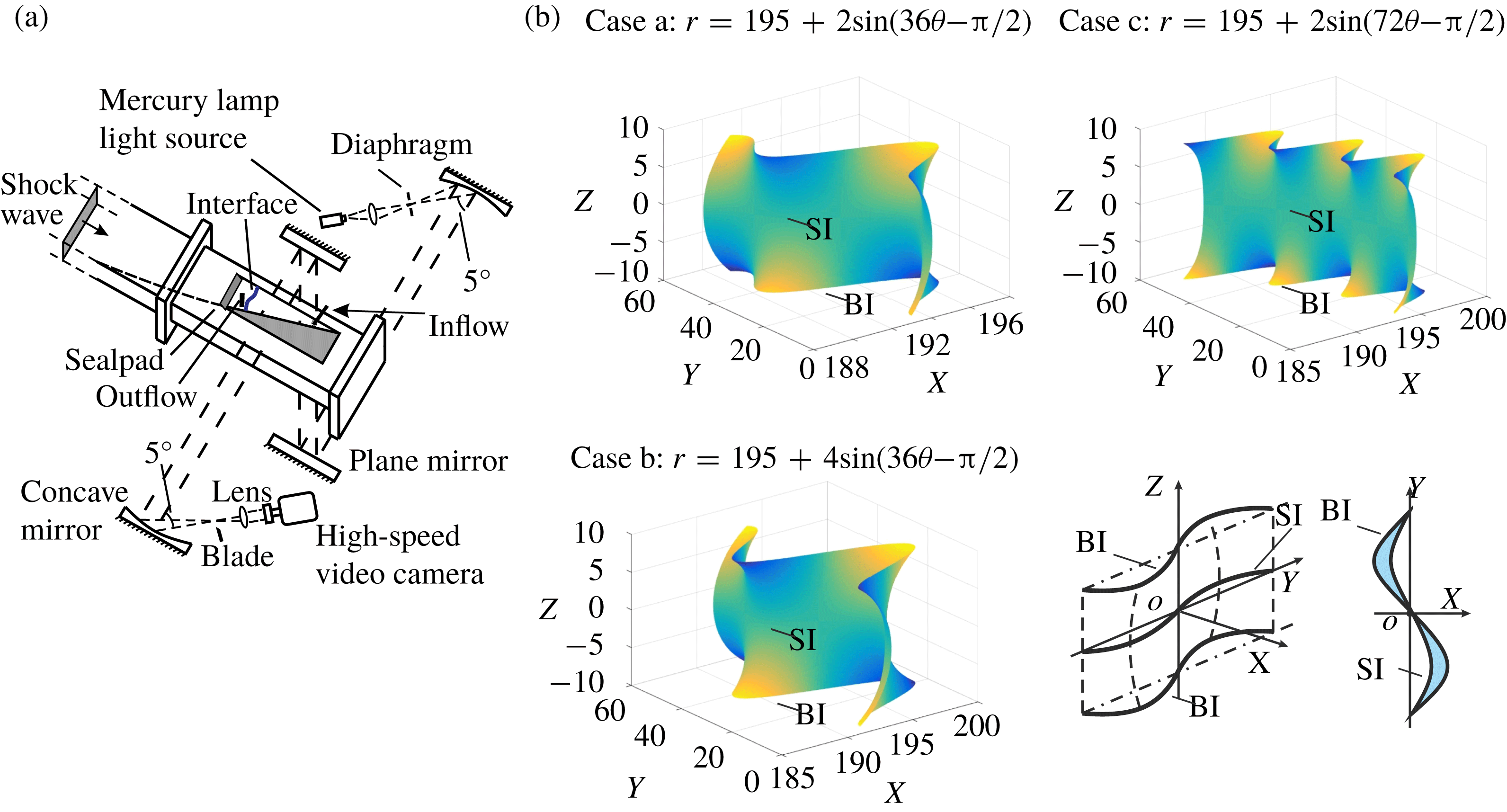
Figure 2. Schematic of schlieren photography system (a), and the three sinusoidal interfaces with a sketch of the minimum surface feature and a top view of the interface (b). BI: boundary interface, SI: symmetry interface.
The formed interface has a zero mean curvature because the gases on both sides are at ambient pressure. Therefore, it is characterized as a minimum surface (Luo, Wang & Si Reference Luo, Wang and Si2013) and presents a three-dimensional (3-D) feature. In a cylindrical coordinate system (
![]() $r,\unicode[STIX]{x1D703},z$
), with
$r,\unicode[STIX]{x1D703},z$
), with
![]() $r$
,
$r$
,
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $z$
being the radius, angle and height, respectively, the minimum surface can be described as a vector
$z$
being the radius, angle and height, respectively, the minimum surface can be described as a vector
![]() $\boldsymbol{R}=(r\cos \unicode[STIX]{x1D703},r\sin \unicode[STIX]{x1D703},z)$
. Deduced by differential geometry in an arbitrary curved surface, the zero mean curvature equation can be expressed as follows (Isenberg Reference Isenberg1992):
$\boldsymbol{R}=(r\cos \unicode[STIX]{x1D703},r\sin \unicode[STIX]{x1D703},z)$
. Deduced by differential geometry in an arbitrary curved surface, the zero mean curvature equation can be expressed as follows (Isenberg Reference Isenberg1992):
where
with subscripts denoting partial derivatives and
![]() $D=\sqrt{EG-F^{2}}$
. From (2.1), the interface surface can be described as:
$D=\sqrt{EG-F^{2}}$
. From (2.1), the interface surface can be described as:
Three interfaces (Cases a, b and c) with different sinusoidal boundary constraints are formed in the present study. The initial amplitude (
![]() $a_{0}$
defined as the half-width from crest to trough) and azimuthal wavenumber (
$a_{0}$
defined as the half-width from crest to trough) and azimuthal wavenumber (
![]() $n$
) of the three configurations are, respectively,
$n$
) of the three configurations are, respectively,
![]() $(a_{0},n)=$
(2 mm, 36), (4 mm, 36) and (2 mm, 72). The boundary of the sinusoidal constraint,
$(a_{0},n)=$
(2 mm, 36), (4 mm, 36) and (2 mm, 72). The boundary of the sinusoidal constraint,
![]() $r=R_{0}+a_{0}\sin (n\unicode[STIX]{x1D703}-\unicode[STIX]{x03C0}/2)$
, generates a minimum surface as
$r=R_{0}+a_{0}\sin (n\unicode[STIX]{x1D703}-\unicode[STIX]{x03C0}/2)$
, generates a minimum surface as
where the amplitude,
![]() $a(z)$
, in each height (
$a(z)$
, in each height (
![]() $z$
) can be acquired by numerically solving equation (2.4) with
$z$
) can be acquired by numerically solving equation (2.4) with
![]() $R_{i}$
the symmetry radius (at
$R_{i}$
the symmetry radius (at
![]() $z=0$
). Therefore, the interfacial amplitude at each cross profile is different, as shown in figure 2(b). Specifically, the minimum amplitudes,
$z=0$
). Therefore, the interfacial amplitude at each cross profile is different, as shown in figure 2(b). Specifically, the minimum amplitudes,
![]() $a_{i}$
, are all located at the symmetry plane and are, respectively, 0.722 mm, 1.391 mm and 0.136 mm. Therefore, the boundary interface (BI, the cross-profile at the boundary plane) has a larger amplitude than the symmetry interface (SI, the cross-profile at the symmetry plane), i.e. the BI and SI have a sinusoidal shape with the same wavenumber but with different amplitudes.
$a_{i}$
, are all located at the symmetry plane and are, respectively, 0.722 mm, 1.391 mm and 0.136 mm. Therefore, the boundary interface (BI, the cross-profile at the boundary plane) has a larger amplitude than the symmetry interface (SI, the cross-profile at the symmetry plane), i.e. the BI and SI have a sinusoidal shape with the same wavenumber but with different amplitudes.
3 Unperturbed interface
To obtain the flow characteristics after the shock–interface interaction in the convergent geometry, the unsteady moving feature of an unperturbed (i.e. the amplitude of the initial interface is
![]() $a_{0}=0$
) air/
$a_{0}=0$
) air/
![]() $\text{SF}_{6}$
cylindrical interface is first studied. As shown in figure 3, owing to the limited range of observation and light blocking of the interface generation device, only the central part of the test section is visualized. A circular constraint at the boundaries (
$\text{SF}_{6}$
cylindrical interface is first studied. As shown in figure 3, owing to the limited range of observation and light blocking of the interface generation device, only the central part of the test section is visualized. A circular constraint at the boundaries (
![]() $r=R_{0}$
) is used, which generates a minimum surface of
$r=R_{0}$
) is used, which generates a minimum surface of
![]() $r=R_{i}\cosh (z/R_{i})$
, where
$r=R_{i}\cosh (z/R_{i})$
, where
![]() $z\in (-d_{0}/2,d_{0}/2)$
and
$z\in (-d_{0}/2,d_{0}/2)$
and
![]() $R_{i}=194.79$
mm at
$R_{i}=194.79$
mm at
![]() $z=0$
. Because the symmetry radius
$z=0$
. Because the symmetry radius
![]() $R_{i}$
is almost identical to the boundary radius (
$R_{i}$
is almost identical to the boundary radius (
![]() $R_{0}$
), the 3-D characteristics of the unperturbed interface are negligible, coinciding with the schlieren images. As can be seen from the movement of an unperturbed interface accelerated by a cylindrically converging shock wave, the interface thickness has no obvious increase. Moreover, under the conditions of the incident shock
$R_{0}$
), the 3-D characteristics of the unperturbed interface are negligible, coinciding with the schlieren images. As can be seen from the movement of an unperturbed interface accelerated by a cylindrically converging shock wave, the interface thickness has no obvious increase. Moreover, under the conditions of the incident shock
![]() $M_{s}=1.2$
and the experimental duration of approximately 1 ms, the thickness of the boundary layers on the top and bottom walls of the test section is estimated to be of the order of 0.5 mm (
$M_{s}=1.2$
and the experimental duration of approximately 1 ms, the thickness of the boundary layers on the top and bottom walls of the test section is estimated to be of the order of 0.5 mm (
![]() ${\sim}4.9\times \sqrt{\unicode[STIX]{x1D707}t/\unicode[STIX]{x1D70C}}$
, where the viscosity of air is
${\sim}4.9\times \sqrt{\unicode[STIX]{x1D707}t/\unicode[STIX]{x1D70C}}$
, where the viscosity of air is
![]() $\unicode[STIX]{x1D707}=1.79\times 10^{-5}~\text{Pa}~\text{s}^{-1}$
and the density of air is
$\unicode[STIX]{x1D707}=1.79\times 10^{-5}~\text{Pa}~\text{s}^{-1}$
and the density of air is
![]() $\unicode[STIX]{x1D70C}=1.2~\text{kg}~\text{m}^{-3}$
at the pressure of 101 325 Pa and the temperature of 293 K), which is far smaller than the thickness of the shock tube test section. These indicate that the boundary layer effects are not significant and can be ignored at least for the time studied in the present work.
$\unicode[STIX]{x1D70C}=1.2~\text{kg}~\text{m}^{-3}$
at the pressure of 101 325 Pa and the temperature of 293 K), which is far smaller than the thickness of the shock tube test section. These indicate that the boundary layer effects are not significant and can be ignored at least for the time studied in the present work.

Figure 3. Schlieren pictures showing the evolution of an unperturbed air/
![]() $\text{SF}_{6}$
interface subjected to a cylindrically converging shock wave. TS, transmitted shock; RTS, reflected shock of TS from the focusing centre; TRTS, transmitted shock of RTS from the interface. Numbers denote time in
$\text{SF}_{6}$
interface subjected to a cylindrically converging shock wave. TS, transmitted shock; RTS, reflected shock of TS from the focusing centre; TRTS, transmitted shock of RTS from the interface. Numbers denote time in
![]() $\unicode[STIX]{x03BC}$
s.
$\unicode[STIX]{x03BC}$
s.
The initial time (
![]() $t=0~\unicode[STIX]{x03BC}$
s defined as the moment when the incident shock arrives at
$t=0~\unicode[STIX]{x03BC}$
s defined as the moment when the incident shock arrives at
![]() $R_{0}$
) is deduced from the location and velocity of the transmitted shock (TS). Time variations of radii of the interface and shock waves including the TS, the reflected shock of TS from the convergence centre (RTS) and the transmitted shock of RTS from the interface (TRTS) are acquired. As plotted in figure 4, the interface movement is classified by three regions of I, II and III based on different time zones. In regions I and II, the interface first experiences a nearly constant movement and then a deceleration process before the reshock (defined as the impact by the RTS). When the TS has moved far away from the interface, an inward deceleration process of the interface is clearly captured, denoted by the red dashed line in figure 4. As we know, when the convergent shock moves inwards, the post-shock flow velocity is increasing. Before the convergent shock approaches the centre, the post-shock flow velocity is subsonic, and the subsonic flow will be accelerated during the propagation along a convergent tube. As a result, the interface will be accelerated. When the shock approaches the convergent centre, the shock Mach number exceeds approximately 2.1 (Zhai et al.
Reference Zhai, Si, Luo, Yang, Liu, Tan and Zou2012), and the post-shock flow velocity will exceed the local sound speed. For a supersonic flow travelling in a convergent tube, the flow velocity will be decreasing. Consequently the flow will be blocked, resulting in the deceleration of the interface. The blockage of the flow is ascribed to the distribution of high pressure. Under the assumption of strong shock wave, Chisnell (Reference Chisnell1998) theoretically deduced that when the specific heat ratio is smaller than 2, the maximum pressure behind the shock is distributed in the region away from the shock front, but not the region just behind the shock front. The higher of shock intensity, the longer the distance of the maximum pressure away from the shock front. In this work, when the shock approaches the convergent centre, the assumption of a strong shock is satisfied, and the maximum pressure zone is formed away from the shock front, resulting in the block of the flow, and further the deceleration of the interface. After the reshock in region III, the interface moves outwards with a deceleration. During this stage, the post-shock flow is subsonic. For a shock wave travelling in a divergent tube, the shock intensity is decreasing, accompanied by the decrease of the flow velocity. Also for the propagation of subsonic flow along a divergent tube, the post-shock flow velocity is also decreasing. The reduction of flow velocity before the interface will result in the deceleration of the interface movement. These decelerations would introduce RT effects on the interface evolution if the initial interface is weakly perturbed, which has been reported in experiments on the OMEGA laser (Lanier et al.
Reference Lanier, Barnes, Batha, Day, Magelssen, Scott, Dunne, Parker and Rothman2003) and in converging shock tube experiments (Ding et al.
Reference Ding, Si, Yang, Lu, Zhai and Luo2017; Lei et al.
Reference Lei, Ding, Si, Zhai and Luo2017). It is clear that the transition between regions II and III is the reshock impact by the reflected shock from the convergence centre. The transition between regions I and II is classified by whether the whole interface enters the deceleration stage. Note that in the experiment, this classification is not accurate enough and has a certain amount of error. However, the deceleration process of the interface will not be influenced.
$R_{0}$
) is deduced from the location and velocity of the transmitted shock (TS). Time variations of radii of the interface and shock waves including the TS, the reflected shock of TS from the convergence centre (RTS) and the transmitted shock of RTS from the interface (TRTS) are acquired. As plotted in figure 4, the interface movement is classified by three regions of I, II and III based on different time zones. In regions I and II, the interface first experiences a nearly constant movement and then a deceleration process before the reshock (defined as the impact by the RTS). When the TS has moved far away from the interface, an inward deceleration process of the interface is clearly captured, denoted by the red dashed line in figure 4. As we know, when the convergent shock moves inwards, the post-shock flow velocity is increasing. Before the convergent shock approaches the centre, the post-shock flow velocity is subsonic, and the subsonic flow will be accelerated during the propagation along a convergent tube. As a result, the interface will be accelerated. When the shock approaches the convergent centre, the shock Mach number exceeds approximately 2.1 (Zhai et al.
Reference Zhai, Si, Luo, Yang, Liu, Tan and Zou2012), and the post-shock flow velocity will exceed the local sound speed. For a supersonic flow travelling in a convergent tube, the flow velocity will be decreasing. Consequently the flow will be blocked, resulting in the deceleration of the interface. The blockage of the flow is ascribed to the distribution of high pressure. Under the assumption of strong shock wave, Chisnell (Reference Chisnell1998) theoretically deduced that when the specific heat ratio is smaller than 2, the maximum pressure behind the shock is distributed in the region away from the shock front, but not the region just behind the shock front. The higher of shock intensity, the longer the distance of the maximum pressure away from the shock front. In this work, when the shock approaches the convergent centre, the assumption of a strong shock is satisfied, and the maximum pressure zone is formed away from the shock front, resulting in the block of the flow, and further the deceleration of the interface. After the reshock in region III, the interface moves outwards with a deceleration. During this stage, the post-shock flow is subsonic. For a shock wave travelling in a divergent tube, the shock intensity is decreasing, accompanied by the decrease of the flow velocity. Also for the propagation of subsonic flow along a divergent tube, the post-shock flow velocity is also decreasing. The reduction of flow velocity before the interface will result in the deceleration of the interface movement. These decelerations would introduce RT effects on the interface evolution if the initial interface is weakly perturbed, which has been reported in experiments on the OMEGA laser (Lanier et al.
Reference Lanier, Barnes, Batha, Day, Magelssen, Scott, Dunne, Parker and Rothman2003) and in converging shock tube experiments (Ding et al.
Reference Ding, Si, Yang, Lu, Zhai and Luo2017; Lei et al.
Reference Lei, Ding, Si, Zhai and Luo2017). It is clear that the transition between regions II and III is the reshock impact by the reflected shock from the convergence centre. The transition between regions I and II is classified by whether the whole interface enters the deceleration stage. Note that in the experiment, this classification is not accurate enough and has a certain amount of error. However, the deceleration process of the interface will not be influenced.
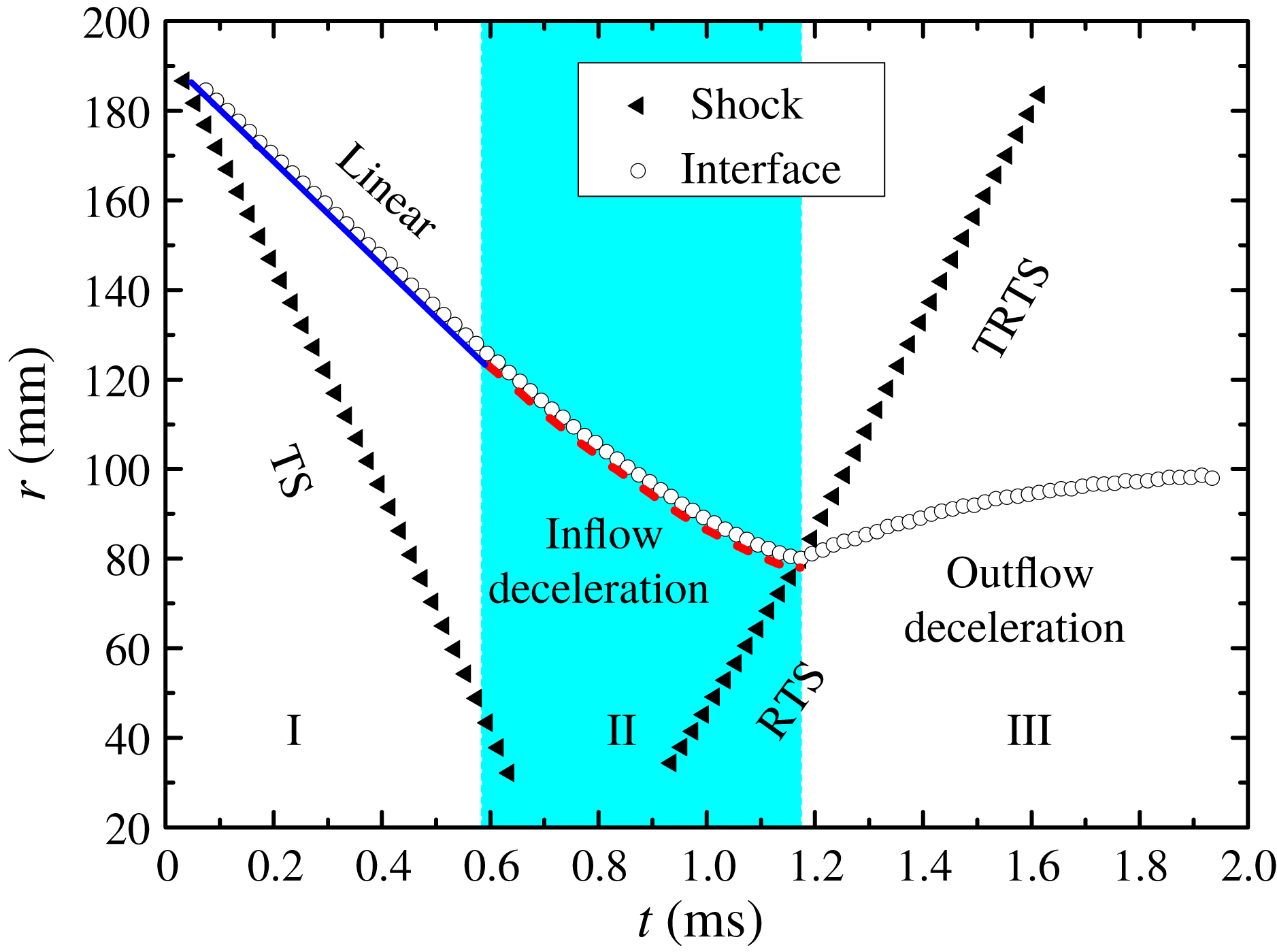
Figure 4. The
![]() $r$
–
$r$
–
![]() $t$
diagram showing the locations of the interface and shock waves in unperturbed air/
$t$
diagram showing the locations of the interface and shock waves in unperturbed air/
![]() $\text{SF}_{6}$
case. The labels are the same as those in figure 3.
$\text{SF}_{6}$
case. The labels are the same as those in figure 3.
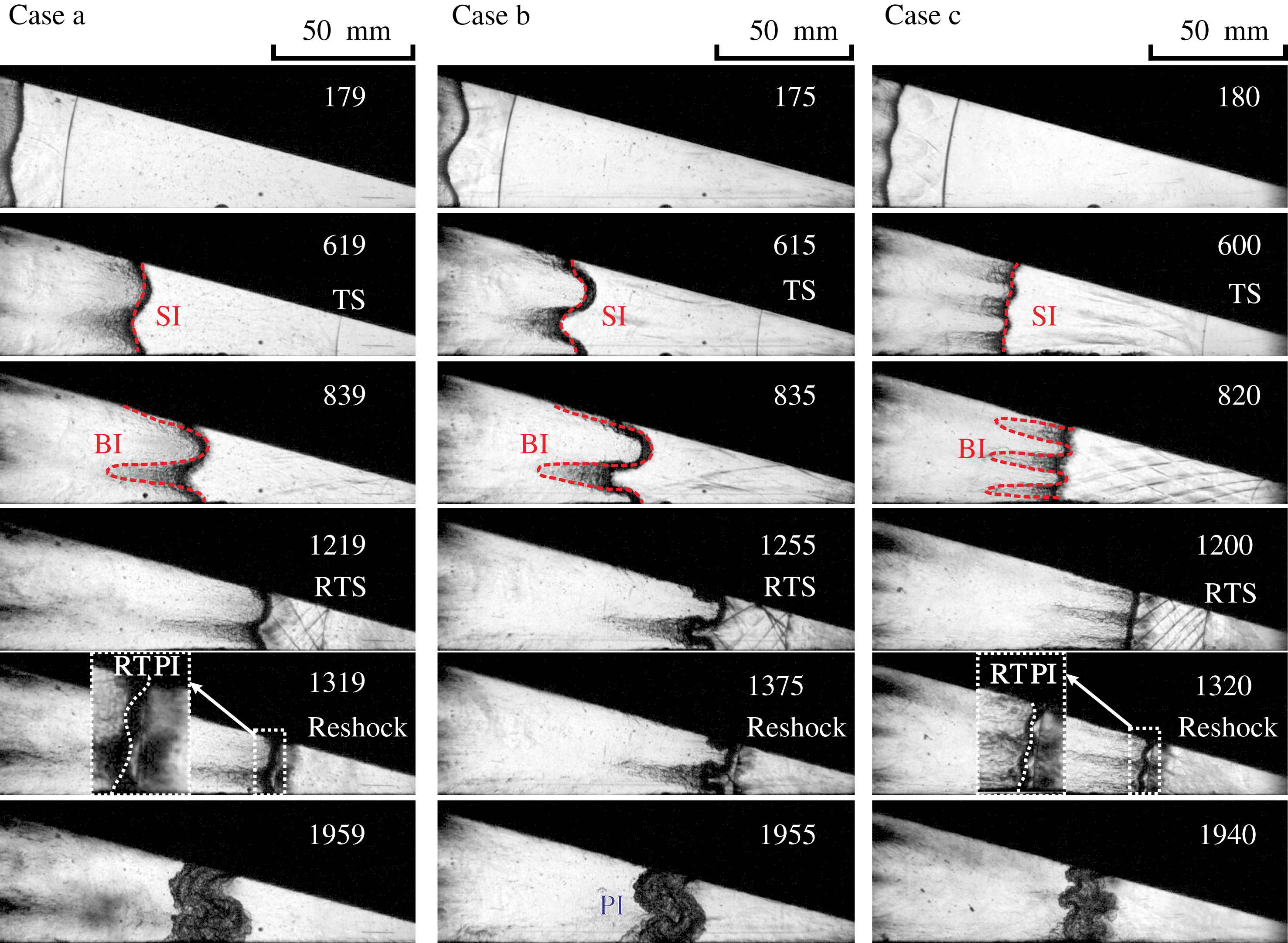
Figure 5. Schlieren photographs showing the evolution of the sinusoidal minimum air/
![]() $\text{SF}_{6}$
interface subjected to the cylindrically converging shock. The inset pictures represent the interface detail when the RTPI has occurred with the white dashed lines denoting the location of the inverted SI. Red dashed lines indicate the locations of the SI and BI. PI, phase inversion; RTPI, phase inversion caused by RT stabilization effect. Dotted lines denote the symmetry interface when the RTPI occurs in Cases a and c. Other labels are the same as those in figure 3. Numbers denote time in
$\text{SF}_{6}$
interface subjected to the cylindrically converging shock. The inset pictures represent the interface detail when the RTPI has occurred with the white dashed lines denoting the location of the inverted SI. Red dashed lines indicate the locations of the SI and BI. PI, phase inversion; RTPI, phase inversion caused by RT stabilization effect. Dotted lines denote the symmetry interface when the RTPI occurs in Cases a and c. Other labels are the same as those in figure 3. Numbers denote time in
![]() $\unicode[STIX]{x03BC}$
s.
$\unicode[STIX]{x03BC}$
s.
4 Single-mode interface
The schlieren frames illustrated in figure 5 provide the representative moments in the three perturbed cases, all showing a 3-D feature of the minimum surface. As sketched in figure 2(b), the interfaces can be separately described as a symmetry interface (SI, at
![]() $z=0$
) and two boundary interfaces (BIs, at
$z=0$
) and two boundary interfaces (BIs, at
![]() $z=\pm d_{0}/2$
). For SIs, the crest and trough develop symmetrically at early times due to small amplitude–wavelength ratios (0.0212, 0.0409 and 0.008, respectively). The BIs quickly develop into the nonlinear stage with the appearances of bubble structure pointing inward and spike structure pointing outward because of their larger amplitude–wavelength ratios (0.0588, 0.1175 and 0.1175, respectively). The reshock occurs at different times in three cases for slight differences of
$z=\pm d_{0}/2$
). For SIs, the crest and trough develop symmetrically at early times due to small amplitude–wavelength ratios (0.0212, 0.0409 and 0.008, respectively). The BIs quickly develop into the nonlinear stage with the appearances of bubble structure pointing inward and spike structure pointing outward because of their larger amplitude–wavelength ratios (0.0588, 0.1175 and 0.1175, respectively). The reshock occurs at different times in three cases for slight differences of
![]() $\text{SF}_{6}$
concentration in the test section (volume fractions of
$\text{SF}_{6}$
concentration in the test section (volume fractions of
![]() $\text{SF}_{6}$
are 79.4 %, 89.7 % and 80.1 %, respectively). The interface amplitudes increase for the SI and BIs after the impact. After a certain period, a reduction of the SI amplitude is observed before the reshock in all cases. A phase inversion (PI, the crest and trough exchange their positions) before the reshock is observed on the SI in Cases a and c. Usually, the PI in the RM instability occurs when a shock wave collides with a heavy/light interface. This is the first time this phase inversion in a light/heavy case has been observed, and it is attributed to the strong and long-term effect of RT stabilization (this phase inversion is called RTPI for differentiating it from the PI when a shock moves from heavy to light). The absence of the RTPI in Case b indicates that the strength and effective time of the deceleration cannot trigger the RTPI on the interface with such a large initial amplitude. However, the SI in Case b experiences a PI after the reshock. Finally, the interface enters a turbulent state after the reshock in all cases.
$\text{SF}_{6}$
are 79.4 %, 89.7 % and 80.1 %, respectively). The interface amplitudes increase for the SI and BIs after the impact. After a certain period, a reduction of the SI amplitude is observed before the reshock in all cases. A phase inversion (PI, the crest and trough exchange their positions) before the reshock is observed on the SI in Cases a and c. Usually, the PI in the RM instability occurs when a shock wave collides with a heavy/light interface. This is the first time this phase inversion in a light/heavy case has been observed, and it is attributed to the strong and long-term effect of RT stabilization (this phase inversion is called RTPI for differentiating it from the PI when a shock moves from heavy to light). The absence of the RTPI in Case b indicates that the strength and effective time of the deceleration cannot trigger the RTPI on the interface with such a large initial amplitude. However, the SI in Case b experiences a PI after the reshock. Finally, the interface enters a turbulent state after the reshock in all cases.
Because the BIs in the schlieren images are so faint that it is difficult to extract reliable data, we shall focus on the SI evolution. Note that in our previous work (Luo et al. Reference Luo, Wang and Si2013) which dealt with the same type interface impacted by a planar shock, the evolution of the inner layer was also captured by the schlieren technique and reliable data were extracted. Using the same method, the SI evolution after the converging shock impact is obtained here. Due to the very slender test section, the geometry convergence effect may be insignificant at early times. Therefore, the early variations of the SI amplitude with time can be described by a 3-D impulsive model extended from the 2-D impulsive model (Luo et al. Reference Luo, Wang and Si2013).
Based on the previous work (Luo et al. Reference Luo, Wang and Si2013), an arbitrary 3-D multi-mode initial interface can be described as,
where
![]() $\unicode[STIX]{x1D702}$
represents the coordinate of the interface based on the moving coordinate system,
$\unicode[STIX]{x1D702}$
represents the coordinate of the interface based on the moving coordinate system,
![]() $k_{x}$
and
$k_{x}$
and
![]() $k_{z}$
are wavenumbers in the x and z directions, respectively,
$k_{z}$
are wavenumbers in the x and z directions, respectively,
![]() $a(k_{x},k_{z})$
,
$a(k_{x},k_{z})$
,
![]() $\unicode[STIX]{x1D719}_{k_{x}}$
and
$\unicode[STIX]{x1D719}_{k_{x}}$
and
![]() $\unicode[STIX]{x1D719}_{k_{z}}$
are, respectively, the corresponding perturbation amplitude and phases, and
$\unicode[STIX]{x1D719}_{k_{z}}$
are, respectively, the corresponding perturbation amplitude and phases, and
![]() $t_{0}$
is the initial time.
$t_{0}$
is the initial time.
During the linear stage, the multi-mode disturbance can be treated as a linear superposition of each single-mode disturbance. Therefore, the linear growth of a 3-D multi-mode disturbance can be expressed as,
where
Here,
![]() $t_{0}^{+}$
is the time just after the impact of incident shock,
$t_{0}^{+}$
is the time just after the impact of incident shock,
![]() $z_{c}$
is the compression ratio and
$z_{c}$
is the compression ratio and
![]() $A^{+}$
is post-shock Atwood number.
$A^{+}$
is post-shock Atwood number.
In this work, the change of growth rate at early times can be neglected due to the large initial interface radius, and the 3-D multi-mode impulsive model can be applied. Therefore,
![]() $k_{x}$
is replaced by
$k_{x}$
is replaced by
![]() $n/R_{0}$
in (4.1) and (4.3), neglecting the weak BP effect at early times and approximately regarding this converging RM configuration as a planar RM configuration. In the converging minimum surface equation (i.e. (2.5)), the first term plays an insignificant role, and it is regarded as a constant in the calculation of the linear growth rate. Based on these assumptions, the disturbance of the minimum surface can be treated as
$n/R_{0}$
in (4.1) and (4.3), neglecting the weak BP effect at early times and approximately regarding this converging RM configuration as a planar RM configuration. In the converging minimum surface equation (i.e. (2.5)), the first term plays an insignificant role, and it is regarded as a constant in the calculation of the linear growth rate. Based on these assumptions, the disturbance of the minimum surface can be treated as
Obviously, there is only one mode in the x direction, and we can use a discrete Fourier transform to analyse the multi-mode in the z direction. Then, the influence on the symmetry plane (
![]() $z=0$
) caused by the minimum surface feature can be evaluated as
$z=0$
) caused by the minimum surface feature can be evaluated as
 $$\begin{eqnarray}g=\frac{\displaystyle \mathop{\sum }_{k_{z}}a(k_{x},k_{z})\sqrt{{k_{x}}^{2}+{k_{z}}^{2}}\cos (\unicode[STIX]{x1D719}_{k_{z}})}{a(z=0)k_{x}}.\end{eqnarray}$$
$$\begin{eqnarray}g=\frac{\displaystyle \mathop{\sum }_{k_{z}}a(k_{x},k_{z})\sqrt{{k_{x}}^{2}+{k_{z}}^{2}}\cos (\unicode[STIX]{x1D719}_{k_{z}})}{a(z=0)k_{x}}.\end{eqnarray}$$
The interface geometry factors
![]() $g$
at the symmetry plane are calculated to be 0.569, 0.561 and 0.418 for Cases a, b and c according to their initially principal curvatures, respectively.
$g$
at the symmetry plane are calculated to be 0.569, 0.561 and 0.418 for Cases a, b and c according to their initially principal curvatures, respectively.
Table 1. Physical parameters of the three cases studied:
![]() $a_{0}$
and
$a_{0}$
and
![]() $a_{i}$
are respectively the initial amplitudes of the boundary plane and the symmetry plane,
$a_{i}$
are respectively the initial amplitudes of the boundary plane and the symmetry plane,
![]() $n$
and
$n$
and
![]() $\unicode[STIX]{x1D706}$
are azimuthal wavenumber and wavelength, respectively,
$\unicode[STIX]{x1D706}$
are azimuthal wavenumber and wavelength, respectively,
![]() $\unicode[STIX]{x1D711}$
is the volume fraction of
$\unicode[STIX]{x1D711}$
is the volume fraction of
![]() $\text{SF}_{6}$
,
$\text{SF}_{6}$
,
![]() $A^{+}$
is the post-shock Atwood number,
$A^{+}$
is the post-shock Atwood number,
![]() $\unicode[STIX]{x0394}v$
is the velocity jump of the interface,
$\unicode[STIX]{x0394}v$
is the velocity jump of the interface,
![]() $v_{i}^{exp}$
is the linear growth rate of the symmetry interface from experiment,
$v_{i}^{exp}$
is the linear growth rate of the symmetry interface from experiment,
![]() $v_{i}^{3D}$
and
$v_{i}^{3D}$
and
![]() $v_{i}^{2D}$
are linear growth rates of the symmetry interface from three-dimensional and two-dimensional theories, respectively,
$v_{i}^{2D}$
are linear growth rates of the symmetry interface from three-dimensional and two-dimensional theories, respectively,
![]() $\unicode[STIX]{x1D70F}_{linear}=n{v_{i}}^{exp}t/R$
is the dimensionless time of the linear stage. Amplitude is in mm and growth rate is in
$\unicode[STIX]{x1D70F}_{linear}=n{v_{i}}^{exp}t/R$
is the dimensionless time of the linear stage. Amplitude is in mm and growth rate is in
![]() $\text{m}~\text{s}^{-1}$
.
$\text{m}~\text{s}^{-1}$
.

Thus, the 3-D impulsive growth rate is acquired as
where
![]() ${\dot{a}}$
denotes the growth rate of the SI amplitude,
${\dot{a}}$
denotes the growth rate of the SI amplitude,
![]() $a_{i}^{+}$
and
$a_{i}^{+}$
and
![]() $\unicode[STIX]{x0394}V$
are respectively the post-shock amplitude and interface velocity. The related physical parameters in the three cases are listed in table 1. Perturbation amplitude and time are, respectively, normalized by the initial amplitude and the duration for the density interface moving from
$\unicode[STIX]{x0394}V$
are respectively the post-shock amplitude and interface velocity. The related physical parameters in the three cases are listed in table 1. Perturbation amplitude and time are, respectively, normalized by the initial amplitude and the duration for the density interface moving from
![]() $R_{i}$
to the geometry centre at its initial velocity obtained by the shock impact, i.e.
$R_{i}$
to the geometry centre at its initial velocity obtained by the shock impact, i.e.
![]() $\unicode[STIX]{x1D70F}=t\unicode[STIX]{x0394}V/R_{i}$
. It can be clearly seen in figure 6 that the amplitude growth with the minimum surface feature is much slower than that obtained by the 2-D impulsive model, and agrees very well with the prediction by the 3-D impulsive model (Luo et al.
Reference Luo, Wang and Si2013) which considers the 3-D effect (supplementary data are available at https://doi.org/10.1017/jfm.2018.424). This slowness can be ascribed to the opposite principal curvatures in vertical and horizontal directions of the minimum surface, which induce opposite pressure gradients and baroclinic vorticity. The good agreement between the experimental result and the 3-D impulsive model also confirms that the BP effect in this slender situation is so weak that it can even be neglected.
$\unicode[STIX]{x1D70F}=t\unicode[STIX]{x0394}V/R_{i}$
. It can be clearly seen in figure 6 that the amplitude growth with the minimum surface feature is much slower than that obtained by the 2-D impulsive model, and agrees very well with the prediction by the 3-D impulsive model (Luo et al.
Reference Luo, Wang and Si2013) which considers the 3-D effect (supplementary data are available at https://doi.org/10.1017/jfm.2018.424). This slowness can be ascribed to the opposite principal curvatures in vertical and horizontal directions of the minimum surface, which induce opposite pressure gradients and baroclinic vorticity. The good agreement between the experimental result and the 3-D impulsive model also confirms that the BP effect in this slender situation is so weak that it can even be neglected.
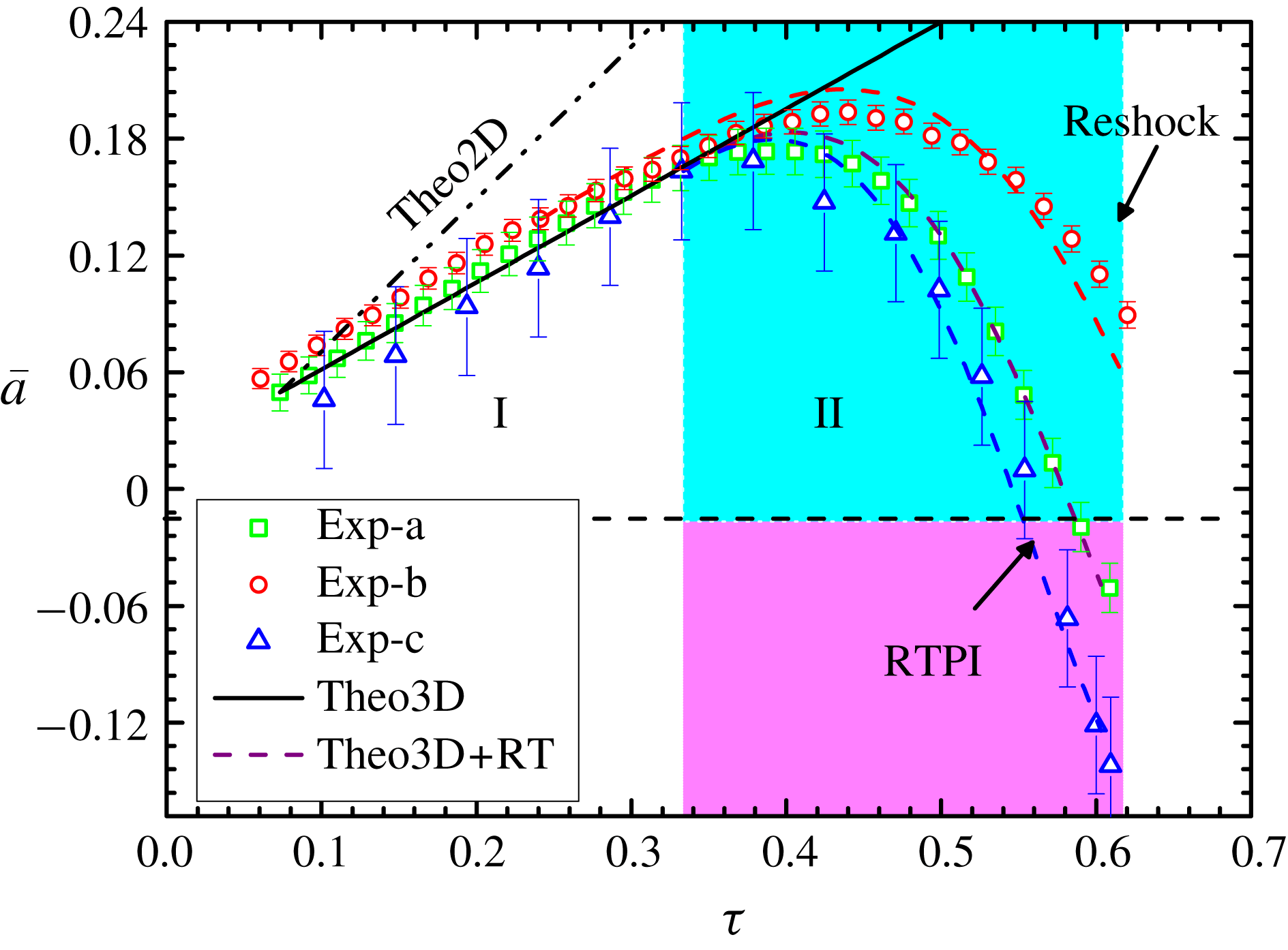
Figure 6. Time variations of amplitude from experiment with error bars and theoretical predictions for symmetry interfaces in three cases (a, b and c). Exp, experimental result; Theo2D, 2-D theoretical result for Case a; Theo3D, 3-D theoretical result for Case a; Theo3D
![]() $+$
RT, 3-D theoretical result including the RT effect.
$+$
RT, 3-D theoretical result including the RT effect.
After the linear stage, the amplitude starts to drop quickly, which indicates that the RT stabilization effect becomes effective. By using the end time of the linear stage from the 3-D impulsive model as the starting point, and considering the RT effect, Bell’s theory can be modified as
where
![]() $R$
is the mean radius of the interface,
$R$
is the mean radius of the interface,
![]() $\ddot{R}$
is its second derivative with time,
$\ddot{R}$
is its second derivative with time,
![]() $t_{\ast }^{+}$
stands for the time just after the linear stage,
$t_{\ast }^{+}$
stands for the time just after the linear stage,
![]() $R_{\ast }$
is the interfacial radius at this moment (
$R_{\ast }$
is the interfacial radius at this moment (
![]() $t_{\ast }^{+}$
) and
$t_{\ast }^{+}$
) and
![]() $A$
is the pre-shock Atwood number. The first term in the right-hand side of equation (4.7) corresponds to the 3-D RM instability, and the second term to the RT effect related to the non-uniform motion of interface with a decay factor
$A$
is the pre-shock Atwood number. The first term in the right-hand side of equation (4.7) corresponds to the 3-D RM instability, and the second term to the RT effect related to the non-uniform motion of interface with a decay factor
![]() $Z$
(Ding et al.
Reference Ding, Si, Yang, Lu, Zhai and Luo2017). The factor
$Z$
(Ding et al.
Reference Ding, Si, Yang, Lu, Zhai and Luo2017). The factor
![]() $1/R^{2}$
appearing in both terms represents the BP effect. The decelerations are calculated by performing a second derivative of the interface trajectory and the decay factor
$1/R^{2}$
appearing in both terms represents the BP effect. The decelerations are calculated by performing a second derivative of the interface trajectory and the decay factor
![]() $Z$
is closely related to the flow compressibility. Note that although the initial shock Mach number is only 1.2, the numerical result (Zhai et al.
Reference Zhai, Si, Luo, Yang, Liu, Tan and Zou2012) showed that the shock Mach number can exceed 2.0 when the shock approaches the convergence centre. As a result, the flow compressibility is believed to be considerable and cannot be ignored, especially when the shock wave approaches the convergence centre. Moreover, as evident in the schlieren images, many disturbance waves, following the transmitted shock, continuously interact with the deformed interface at early stages. The flow compressibility caused by these disturbance waves can also inhibit the growth rate of the perturbation amplitude, which has not been considered in the Bell’s theory analysis.
$Z$
is closely related to the flow compressibility. Note that although the initial shock Mach number is only 1.2, the numerical result (Zhai et al.
Reference Zhai, Si, Luo, Yang, Liu, Tan and Zou2012) showed that the shock Mach number can exceed 2.0 when the shock approaches the convergence centre. As a result, the flow compressibility is believed to be considerable and cannot be ignored, especially when the shock wave approaches the convergence centre. Moreover, as evident in the schlieren images, many disturbance waves, following the transmitted shock, continuously interact with the deformed interface at early stages. The flow compressibility caused by these disturbance waves can also inhibit the growth rate of the perturbation amplitude, which has not been considered in the Bell’s theory analysis.
As shown in figure 6, the new model describes the amplitude growing behaviour reasonably well in all cases by using a suitable decay factor
![]() $Z$
(0.55, 0.35 and 0.4 for Cases a, b and c, respectively) and correctly predicts the RTPI in Cases a and c. Because the nonlinearity and 3-D effect can only slow down the growth rate of amplitude, which facilitates the RTPI occurrence but cannot result in a negative growth rate, we believe that they only play a secondary role compared with the RT stabilization effect. As discussed before, the BP effect also plays a minor role on the amplitude variation. Therefore, the RT stabilization effect is the primary factor that results in the amplitude decrease and the RTPI. As a whole, the RM instability promotes the amplitude growth, while the RT stabilization effect inhibits the amplitude growth in this process. The RTPI is a result of the strong and long-term effect of the RT stabilization. In fact, the effective time of RT stabilization effect in Case a is approximately 700
$Z$
(0.55, 0.35 and 0.4 for Cases a, b and c, respectively) and correctly predicts the RTPI in Cases a and c. Because the nonlinearity and 3-D effect can only slow down the growth rate of amplitude, which facilitates the RTPI occurrence but cannot result in a negative growth rate, we believe that they only play a secondary role compared with the RT stabilization effect. As discussed before, the BP effect also plays a minor role on the amplitude variation. Therefore, the RT stabilization effect is the primary factor that results in the amplitude decrease and the RTPI. As a whole, the RM instability promotes the amplitude growth, while the RT stabilization effect inhibits the amplitude growth in this process. The RTPI is a result of the strong and long-term effect of the RT stabilization. In fact, the effective time of RT stabilization effect in Case a is approximately 700
![]() $\unicode[STIX]{x03BC}$
s, which is almost ten times as long as the one in the semi-annular converging shock tube (Ding et al.
Reference Ding, Si, Yang, Lu, Zhai and Luo2017) or in the coaxial converging shock tube (Lei et al.
Reference Lei, Ding, Si, Zhai and Luo2017). Therefore, the RTPI was absent in such a short-term case and only the amplitude reduction was observed in previous studies. However, it should be clearly stated that the theoretical model is a simple model that does not account for the important details of shock–interface interaction, the non-local character and the statistically unsteadiness of the RT/RM dynamics, and further investigations are required. Also, it should be noted that the interface amplitude will start to grow after a certain time because the amplitude
$\unicode[STIX]{x03BC}$
s, which is almost ten times as long as the one in the semi-annular converging shock tube (Ding et al.
Reference Ding, Si, Yang, Lu, Zhai and Luo2017) or in the coaxial converging shock tube (Lei et al.
Reference Lei, Ding, Si, Zhai and Luo2017). Therefore, the RTPI was absent in such a short-term case and only the amplitude reduction was observed in previous studies. However, it should be clearly stated that the theoretical model is a simple model that does not account for the important details of shock–interface interaction, the non-local character and the statistically unsteadiness of the RT/RM dynamics, and further investigations are required. Also, it should be noted that the interface amplitude will start to grow after a certain time because the amplitude
![]() $a$
is negative after the RTPI and the growth rate of the amplitude becomes positive according to equation (4.7). Therefore, it is expected that the interface amplitude will oscillate around zero for a sufficiently long time of deceleration. However, in our experiment, the deceleration time is limited by the length of the converging section of the facility so that only the RTPI is observed and the oscillation of interface amplitude is absent.
$a$
is negative after the RTPI and the growth rate of the amplitude becomes positive according to equation (4.7). Therefore, it is expected that the interface amplitude will oscillate around zero for a sufficiently long time of deceleration. However, in our experiment, the deceleration time is limited by the length of the converging section of the facility so that only the RTPI is observed and the oscillation of interface amplitude is absent.
5 Conclusions
The evolution of perturbed air/
![]() $\text{SF}_{6}$
interfaces subjected to a cylindrically converging shock wave is investigated experimentally in a converging shock tube with a very slender test section. Bounded by the cylindrically sinusoidal boundary, the generated single-mode interface presents 3-D characteristics because of its minimum surface feature, which leads to the stratified evolution of the shocked interface. For the symmetry interfaces, the development of perturbation amplitude is nearly linear at early stages and is much slower than the prediction of the 2-D impulsive model, but coincides well with the prediction of the 3-D linear model which considers the effects of the opposite principal curvatures of the initial interface. A RTPI is found at the symmetry interface with a small initial amplitude, which is the result of the strong and long-term effect of the RT stabilization. This is the first time this RTPI in a light/heavy configuration has been observed and the RTPI may be helpful to find a freezing interface in the ICF. A model combining the 3-D effect and the RT stabilization effect is proposed, which well describes the amplitude growth behaviour including the RTPI by using a suitable decay factor. It is also noted that the nonlinearity and 3-D effect contribute to the reduction of growth rate.
$\text{SF}_{6}$
interfaces subjected to a cylindrically converging shock wave is investigated experimentally in a converging shock tube with a very slender test section. Bounded by the cylindrically sinusoidal boundary, the generated single-mode interface presents 3-D characteristics because of its minimum surface feature, which leads to the stratified evolution of the shocked interface. For the symmetry interfaces, the development of perturbation amplitude is nearly linear at early stages and is much slower than the prediction of the 2-D impulsive model, but coincides well with the prediction of the 3-D linear model which considers the effects of the opposite principal curvatures of the initial interface. A RTPI is found at the symmetry interface with a small initial amplitude, which is the result of the strong and long-term effect of the RT stabilization. This is the first time this RTPI in a light/heavy configuration has been observed and the RTPI may be helpful to find a freezing interface in the ICF. A model combining the 3-D effect and the RT stabilization effect is proposed, which well describes the amplitude growth behaviour including the RTPI by using a suitable decay factor. It is also noted that the nonlinearity and 3-D effect contribute to the reduction of growth rate.
The experimental duration in this work is longer compared with the previous converging RM instability experiments; it seems, however, far from the best duration. The present work is only a starting point, and further investigations are required to understand the properties of the RT/RM dynamics in a convergent geometry. In our laboratory, a converging shock tube with a stronger shock and a larger test section, which can provide a longer duration of test, is under construction. Combined with the particle image velocimetry and planar laser induced fluorescence techniques, more interesting results are expected.
Acknowledgement
This work was supported by the National Key R&D Program of China (no. 2016YFC0800100), National Natural Science Foundation of China (nos 11625211 and 11621202, NSAF U1530103), the China Postdoctoral Science Foundation (2016M602026) and the Science Challenge Project (no. TZ2016001).
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2018.424.










