Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Federrath, Christoph
and
Banerjee, Supratik
2015.
The density structure and star formation rate of non-isothermal polytropic turbulence.
Monthly Notices of the Royal Astronomical Society,
Vol. 448,
Issue. 4,
p.
3297.
Banerjee, S.
Hadid, L. Z.
Sahraoui, F.
and
Galtier, S.
2016.
SCALING OF COMPRESSIBLE MAGNETOHYDRODYNAMIC TURBULENCE IN THE FAST SOLAR WIND.
The Astrophysical Journal Letters,
Vol. 829,
Issue. 2,
p.
L27.
Banerjee, Supratik
and
Kritsuk, Alexei G.
2017.
Exact relations for energy transfer in self-gravitating isothermal turbulence.
Physical Review E,
Vol. 96,
Issue. 5,
Andrés, N.
and
Sahraoui, F.
2017.
Alternative derivation of exact law for compressible and isothermal magnetohydrodynamics turbulence.
Physical Review E,
Vol. 96,
Issue. 5,
Davidovits, Seth
and
Fisch, Nathaniel J.
2017.
A Lower Bound on Adiabatic Heating of Compressed Turbulence for Simulation and Model Validation.
The Astrophysical Journal,
Vol. 838,
Issue. 2,
p.
118.
Raja, K. Sasikumar
Subramanian, Prasad
Ramesh, R.
Vourlidas, Angelos
and
Ingale, Madhusudan
2017.
Turbulent Density Fluctuations and Proton Heating Rate in the Solar Wind from 9–20 R⊙
.
The Astrophysical Journal,
Vol. 850,
Issue. 2,
p.
129.
Andrés, N.
Sahraoui, F.
Galtier, S.
Hadid, L. Z.
Dmitruk, P.
and
Mininni, P. D.
2018.
Energy cascade rate in isothermal compressible magnetohydrodynamic turbulence.
Journal of Plasma Physics,
Vol. 84,
Issue. 4,
Galtier, S
2018.
Turbulence in space plasmas and beyond.
Journal of Physics A: Mathematical and Theoretical,
Vol. 51,
Issue. 29,
p.
293001.
Banerjee, Supratik
and
Kritsuk, Alexei G.
2018.
Energy transfer in compressible magnetohydrodynamic turbulence for isothermal self-gravitating fluids.
Physical Review E,
Vol. 97,
Issue. 2,
Kopyev, A. V.
and
Zybin, K. P.
2018.
Exact result for mixed triple two-point correlations of velocity and velocity gradients in isotropic turbulence.
Journal of Turbulence,
Vol. 19,
Issue. 9,
p.
717.
Eyink, Gregory L.
and
Drivas, Theodore D.
2018.
Cascades and Dissipative Anomalies in Compressible Fluid Turbulence.
Physical Review X,
Vol. 8,
Issue. 1,
Alexakis, A.
and
Biferale, L.
2018.
Cascades and transitions in turbulent flows.
Physics Reports,
Vol. 767-769,
Issue. ,
p.
1.
Gerolymos, G. A.
and
Vallet, I.
2018.
Correlation coefficients of thermodynamic fluctuations in compressible aerodynamic turbulence.
Journal of Fluid Mechanics,
Vol. 851,
Issue. ,
p.
447.
Andrés, Nahuel
and
Banerjee, Supratik
2019.
Statistics of incompressible hydrodynamic turbulence: An alternative approach.
Physical Review Fluids,
Vol. 4,
Issue. 2,
Ferrand, R.
Galtier, S.
Sahraoui, F.
Meyrand, R.
Andrés, N.
and
Banerjee, S.
2019.
On Exact Laws in Incompressible Hall Magnetohydrodynamic Turbulence.
The Astrophysical Journal,
Vol. 881,
Issue. 1,
p.
50.
Mouraya, Sukhdev
and
Banerjee, Supratik
2019.
Determination of energy flux rate in homogeneous ferrohydrodynamic turbulence using two-point statistics.
Physical Review E,
Vol. 100,
Issue. 5,
Beresnyak, Andrey
2019.
MHD turbulence.
Living Reviews in Computational Astrophysics,
Vol. 5,
Issue. 1,
Mohapatra, Rajsekhar
Federrath, Christoph
and
Sharma, Prateek
2020.
Turbulence in stratified atmospheres: implications for the intracluster medium.
Monthly Notices of the Royal Astronomical Society,
Vol. 493,
Issue. 4,
p.
5838.
Girichidis, Philipp
Offner, Stella S. R.
Kritsuk, Alexei G.
Klessen, Ralf S.
Hennebelle, Patrick
Kruijssen, J. M. Diederik
Krause, Martin G. H.
Glover, Simon C. O.
and
Padovani, Marco
2020.
Physical Processes in Star Formation.
Space Science Reviews,
Vol. 216,
Issue. 4,
Xie, Jin-Han
2020.
Quantifying the linear damping in two-dimensional turbulence.
Physical Review Fluids,
Vol. 5,
Issue. 9,
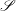 $\mathcal{S}$ which may act as a source or a sink for the mean energy transfer rate. At subsonic scales, we predict dimensionally that the isotropic
$\mathcal{S}$ which may act as a source or a sink for the mean energy transfer rate. At subsonic scales, we predict dimensionally that the isotropic 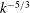 $k^{-5/3}$ energy spectrum for the density-weighted velocity field (
$k^{-5/3}$ energy spectrum for the density-weighted velocity field ( $\rho ^{1/3} \boldsymbol {v}$), previously obtained for isothermal turbulence, is modified by a polytropic contribution, whereas at supersonic scales
$\rho ^{1/3} \boldsymbol {v}$), previously obtained for isothermal turbulence, is modified by a polytropic contribution, whereas at supersonic scales 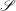 $\mathcal{S}$ may impose another scaling depending on the polytropic index. In both cases, it is shown that the fluctuating sound speed is a key ingredient for understanding polytropic compressible turbulence.
$\mathcal{S}$ may impose another scaling depending on the polytropic index. In both cases, it is shown that the fluctuating sound speed is a key ingredient for understanding polytropic compressible turbulence.