Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T21:01:02.944Z Has data issue: false hasContentIssue false
  • English
  • Français

Instabilities of the flow around a cylinder and emission of vortex dipoles

Published online by Cambridge University Press:  01 August 2013

Ziv Kizner ,
Viacheslav Makarov ,
Leon Kamp  and
GertJan van Heijst
Ziv Kizner*
Affiliation:
Departments of Mathematics and Physics, Bar-Ilan University, Ramat-Gan, 5290002, Israel
Viacheslav Makarov
Affiliation:
Centro Interdisciplinario de Ciencias Marinas, Instituto Politécnico Nacional, La Paz, Baja California Sur 23096, México
Leon Kamp
Affiliation:
Turbulence and Vortex Dynamics Group, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
GertJan van Heijst
Affiliation:
Turbulence and Vortex Dynamics Group, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
*
†Email address for correspondence: Ziv.Kizner@biu.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

Instabilities and long-term evolution of two-dimensional circular flows around a rigid circular cylinder (island) are studied analytically and numerically. For that we consider a base flow consisting of two concentric neighbouring rings of uniform but different vorticity, with the inner ring touching the cylinder. We first study the inviscid linear stability of such flows to perturbations of the free edges of the rings. For a given ratio of the vorticity in the rings, the governing parameters of the problem are the radii of the inner and outer rings scaled on the cylinder radius. In this two-dimensional parameter space, we determine analytically the regions of linear stability/instability of each azimuthal mode 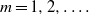$m= 1, 2, \ldots . $ In the physically most meaningful case of zero net circulation, for each mode 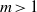$m\gt 1$, two regions are identified: a regular instability region where mode 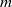$m$ is unstable along with some other modes, and a unique instability region where only mode 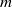$m$ is unstable. After the conditions of linear instability are established, inviscid contour-dynamics and high-Reynolds-number finite-element simulations are conducted. In the regular instability regions, simulations of both kinds typically result in the formation of vortical dipoles or multipoles. In the unique instability regions, where the inner vorticity ring is much thinner than the outer ring, the inviscid contour-dynamics simulations do not reveal dipole emission. In the viscous simulation, because viscosity has time to widen the inner ring, the instability develops in the same manner as in the regular instability regions.

JFM classification

Instability: Instability Vortex Flows: Vortex breakdown Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 419 - 441
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brink, K. H. 1999 Island-trapped waves with applications to observations off Bermuda. Dyn. Atmos. Oceans 29, 93–118.Google Scholar
Carton, X. J. 1992 On the merger of shielded vortices. Europhys. Lett. 18, 697–703.Google Scholar
Chen, C. & Beardsley, R. C. 1995 A numerical study of stratified tidal rectification over finite-amplitude banks. Part I: symmetric banks. J. Phys. Oceanogr. 25, 2090–2110.Google Scholar
Comsol AB, 2012 COMSOL Multiphysics Modelling Guide. Version 4.3.Google Scholar
Coppa, G. G. M., Peano, F. & Peinetti, F. 2002 Image-charge method for contour dynamics in systems with cylindrical boundaries. J. Comput. Phys. 182, 392–417.Google Scholar
Crowdy, D. 2010 A new calculus for two-dimensional vortex dynamics. Theor. Comput. Fluid Dyn. 24, 9–24.CrossRefGoogle Scholar
Crowdy, D. & Surana, A. 2007 Contour dynamics in complex domains. J. Fluid Mech. 593, 235–254.CrossRefGoogle Scholar
Dritschel, D. G. 1988 Contour surgery: a topological reconnection scheme for extended contour integrations using contour dynamics. J. Comput. Phys. 77, 240–266.Google Scholar
Dyke, P. 2005 Wave trapping and flow around an irregular near circular island in a stratified sea. Ocean Dyn. 55, 236–247.CrossRefGoogle Scholar
Elcrat, A., Fornberg, B. & Miller, K. G. 2005 Stability of vortices in equilibrium with a cylinder. J. Fluid Mech. 544, 53–68.Google Scholar
Flierl, G. R. 1988 On the stability of geostrophic vortices. J. Fluid Mech. 197, 349–388.CrossRefGoogle Scholar
Johnson, E. R. & McDonald, N. R. 2004 The motion of a vortex near two circular cylinders. Proc. R. Soc. Lond. A 460, 939–954.CrossRefGoogle Scholar
Kozlov, V. F. 1983 The method of contour dynamics in model problems of the ocean topographic cyclogenesis. Izv. Atmos. Ocean. Phys. 19, 635–640.Google Scholar
Kozlov, V. F. & Makarov, V. G. 1985a Hydrodynamic model for the generation of mushroom-like ocean currents. Dokl. Akad. Nauk SSSR 281, 1213–1215.Google Scholar
Kozlov, V. F. & Makarov, V. G. 1985b Simulation of the instability of axisymmetric vortices using the contour dynamics method. Fluid Dyn. 20, 28–34.CrossRefGoogle Scholar
Loder, J. W. & Wright, D. G. 1985 Tidal rectification and frontal circulation on the sides of Georges Bank. J. Mar. Res. 43, 581–604.Google Scholar
Longuet-Higgins, M. S. 1969 On the trapping of wave long-period waves round islands. J. Fluid Mech. 37, 773–784.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1970 Steady currents induced by oscillations round islands. J. Fluid Mech. 42, 701–720.CrossRefGoogle Scholar
Macaskill, C., Padden, W. E. P. & Dritschel, D. G. 2003 The CASL algorithm for quasi-geostrophic flow in a cylinder. J. Comput. Phys. 188, 232–251.CrossRefGoogle Scholar
Makarov, V. G. 1996 Numerical simulation of the formation of tripolar vortices by the method of contour dynamics. Izv. Atmos. Ocean. Phys. 32, 40–49.Google Scholar
Milne-Thomson, L. M. 1996 Theoretical Hydrodynamics. Dover.Google Scholar
Morel, Y. G & Carton, X. J. 1994 Multipolar vortices in two-dimensional incompressible flows. J. Fluid Mech. 267, 23–51.CrossRefGoogle Scholar
Pedlosky, J., Iacono, R. & Napolitano, E. 2009 The skirted island: the effects of topography on the flow around planetary scale islands. J. Mar. Res. 67 (170), 435–478.Google Scholar
Pullin, D. I. 1992 Contour dynamics methods. Annu. Rev. Fluid Mech. 24, 89–115.Google Scholar
Wright, D. G. & Loder, J. W. 1985 A depth-dependent study of the topographic rectification of tidal currents. Geophys. Astrophys. Fluid Dyn. 31, 169–220.CrossRefGoogle Scholar
Zabusky, N. J., Hughes, M. H. & Roberts, K. V. 1979 Contour dynamics for the Euler equations in two dimensions. J. Comput. Phys. 30, 96–106.CrossRefGoogle Scholar