Hostname: page-component-77c89778f8-cnmwb Total loading time: 0 Render date: 2024-07-18T02:46:23.991Z Has data issue: false hasContentIssue false
  • English
  • Français

High-resolution simulations of cylindrical gravity currents in a rotating system

Published online by Cambridge University Press:  29 September 2016

Albert Dai  and
Ching-Sen Wu
Albert Dai*
Affiliation:
Department of Engineering Science and Ocean Engineering, National Taiwan University, Taiwan
Ching-Sen Wu
Affiliation:
Department of Engineering Science and Ocean Engineering, National Taiwan University, Taiwan
*
†Email address for correspondence: hdai@ntu.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

Cylindrical gravity currents, produced by a full-depth lock release, in a rotating system are investigated by means of three-dimensional high-resolution simulations of the incompressible variable-density Navier–Stokes equations with the Coriolis term and using the Boussinesq approximation for a small density difference. Here, the depth of the fluid is chosen to be the same as the radius of the cylindrical lock and the ambient fluid is non-stratified. Our attention is focused on the situation when the ratio of Coriolis to inertia forces is not large, namely 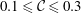$0.1\leqslant {\mathcal{C}}\leqslant 0.3$, and the non-rotating case, namely 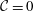${\mathcal{C}}=0$, is also briefly considered. The simulations reproduce the major features observed in the laboratory and provide more detailed flow information. After the heavy fluid contained in a cylindrical lock is released in a rotating system, the influence of the Coriolis effects is not significant during the initial one-tenth of a revolution of the system. During the initial one-tenth of a revolution of the system, Kelvin–Helmholtz vortices form and the rotating cylindrical gravity currents maintain nearly perfect axisymmetry. Afterwards, three-dimensionality of the flow quickly develops and the outer rim of the spreading heavy fluid breaks away from the body of the current, which gives rise to the maximum dissipation rate in the system during the entire adjustment process. The detached outer rim of heavy fluid then continues to propagate outward until a maximum radius of propagation is attained. The body of the current exhibits a complex contraction–relaxation motion and new outwardly propagating pulses form regularly in a period slightly less than half-revolution of the system. Depending on the ratio of Coriolis to inertia forces, such a contraction–relaxation motion may be initiated after or before the attainment of a maximum radius of propagation. In the contraction–relaxation motion of the heavy fluid, energy is transformed between potential energy and kinetic energy, while it is mainly the kinetic energy that is consumed by the dissipation. As a new pulse initially propagates outward, the potential energy in the system increases at the expense of decreasing kinetic energy, until a local maximum of potential energy is reached. During the latter part of the new pulse propagation, the kinetic energy in the system increases at the expense of decreasing potential energy, until a local minimum of potential energy is reached and another new pulse takes form. With the use of three-dimensional high-resolution simulations, the lobe-and-cleft structure at the advancing front can be clearly observed. The number of lobes is maintained only for a limited period of time before merger between existing lobes occurs when a maximum radius of propagation is approached. The high-resolution simulations complement the existing shallow-water formulation, which accurately predicts many important features and provides insights for rotating cylindrical gravity currents with good physical assumptions and simple mathematical models.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Papers
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , pp. 71 - 101
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adduce, C., Sciortino, G. & Proietti, S. 2012 Gravity currents produced by lock-exchanges: experiments and simulations with a two layer shallow-water model with entrainment. ASCE J. Hydraul. Engng 138 (2), 111–121.CrossRefGoogle Scholar
Alahyari, A. & Longmire, E. 1996 Development and structure of a gravity current head. Exp. Fluids 20, 410–416.CrossRefGoogle Scholar
Allen, J. 1985 Principles of Physical Sedimentology. Allen & Unwin.Google Scholar
Birman, V. K., Martin, J. E. & Meiburg, E. 2005 The non-Boussinesq lock-exchange problem. Part 2. High-resolution simulations. J. Fluid Mech. 537, 125–144.CrossRefGoogle Scholar
Bonnecaze, R. T., Hallworth, M. A., Huppert, H. E. & Lister, J. R. 1995 Axisymmetric particle-driven gravity currents. J. Fluid Mech. 294, 93–121.CrossRefGoogle Scholar
Bonometti, T. & Balachandar, S. 2008 Effect of Schmidt number on the structure and propagation of density currents. Theor. Comput. Fluid Dyn. 22, 341–361.CrossRefGoogle Scholar
Cantero, M., Balachandar, S. & Garcia, M. 2007a High-resolution simulations of cylindrical density currents. J. Fluid Mech. 590, 437–469.CrossRefGoogle Scholar
Cantero, M., Balachandar, S., Garcia, M. & Ferry, J. 2006 Direct numerical simulations of planar and cylindrical density currents. Trans. ASME J. Appl. Mech. 73, 923–930.CrossRefGoogle Scholar
Cantero, M., Lee, J., Balachandar, S. & Garcia, M. 2007b On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Csanady, G. T. 1979 The birth and death of a warm core ring. J. Geophys. Res. 84, 777–780.CrossRefGoogle Scholar
Dai, A. 2013 Experiments on gravity currents propagating on different bottom slopes. J. Fluid Mech. 731, 117–141.CrossRefGoogle Scholar
Dai, A. 2014 Non-Boussinesq gravity currents propagating on different bottom slopes. J. Fluid Mech. 741, 650–680.CrossRefGoogle Scholar
Dai, A. 2015 High-resolution simulations of downslope gravity currents in the acceleration phase. Phys. Fluids 27, 076602.CrossRefGoogle Scholar
Dai, A. & Huang, Y.-L. 2016 High-resolution simulations of non-Boussinesq downslope gravity currents in the acceleration phase. Phys. Fluids 28, 026602.CrossRefGoogle Scholar
Dai, A., Ozdemir, C. E., Cantero, M. I. & Balachandar, S. 2012 Gravity currents from instantaneous sources down a slope. ASCE J. Hydraul. Engng 138 (3), 237–246.CrossRefGoogle Scholar
Dewar, W. K. & Killworth, P. D. 1990 On the cylinder collapse problem, mixing and the merger of isolated eddies. J. Phys. Oceanogr. 20, 1563–1575.2.0.CO;2>CrossRefGoogle Scholar
Durran, D. 1999 Numerical Methods for Wave Equations in Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
Flierl, G. R. 1979 A simple model for the structure of warm and cold core rings. J. Geophys. Res. 84, 781–785.CrossRefGoogle Scholar
Griffiths, R. W. 1986 Gravity currents in rotating systems. Annu. Rev. Fluid Mech. 18, 59–89.CrossRefGoogle Scholar
Griffiths, R. W. & Linden, P. F. 1981 The stability of vortices in a rotating, stratified fluid. J. Fluid Mech. 105, 283–316.CrossRefGoogle Scholar
Hallworth, M., Huppert, H., Phillips, J. & Sparks, S. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.CrossRefGoogle Scholar
Hallworth, M. A., Huppert, H. E. & Ungarish, M. 2001 Axisymmetric gravity currents in a rotating system: experimental and numerical investigations. J. Fluid Mech. 447, 1–29.CrossRefGoogle Scholar
Härtel, C., Carlsson, F. & Thunblom, M. 2000a Analysis and direct numerical simulation of the flow at a gravity-current head. Part 2. The lobe-and-cleft instability. J. Fluid Mech. 418, 213–229.CrossRefGoogle Scholar
Härtel, C., Meiburg, E. & Necker, F. 2000b Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. Flow topology and front speed for slip and no-slip boundaries. J. Fluid Mech. 418, 189–212.CrossRefGoogle Scholar
Härtel, C., Michaud, L. K. M. & Stein, C. 1997 A direct numerical simulation approach to the study of intrusion fronts. J. Engng Maths 32, 103–120.CrossRefGoogle Scholar
Huppert, H. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal boundary surface. J. Fluid Mech. 121, 43–58.CrossRefGoogle Scholar
Huppert, H. & Simpson, J. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.CrossRefGoogle Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.CrossRefGoogle Scholar
Huq, P. 1996 The role of aspect ratio on entrainment rates of instantaneous, axisymmetric finite volume releases of dense fluid. J. Hazard. Mater. 49, 89–101.CrossRefGoogle Scholar
Killworth, P. D. 1992 The time-dependent collapse of a rotating fluid cylinder. J. Phys. Oceanogr. 22, 390–397.2.0.CO;2>CrossRefGoogle Scholar
La Rocca, M., Adduce, C., Lombardi, V., Sciortino, G. & Hinkermann, R. 2012a Developement of a lattice Boltzmann method for two-layered shallow-water flow. Intl J. Numer. Meth. Fluids 70 (8), 1048–1072.CrossRefGoogle Scholar
La Rocca, M., Adduce, C., Sciortino, G., Bateman, P. A. & Boniforti, M. A. 2012b A two-layer shallow water model for 3D gravity currents. J. Hydraul. Res. 50 (2), 208–217.CrossRefGoogle Scholar
La Rocca, M., Adduce, C., Sciortino, G. & Pinzon, A. B. 2008 Experimental and numerical simulation of three-dimensional gravity currents on smooth and rough bottom. Phys. Fluids 20 (10), 106603.CrossRefGoogle Scholar
Lombardi, V., Adduce, C., Sciortino, G. & La Rocca, M. 2015 Gravity currents flowing upslope: laboratory experiments and shallow-water simulations. Phys. Fluids 27, 016602.Google Scholar
Marino, B., Thomas, L. & Linden, P. 2005 The front condition for gravity currents. J. Fluid Mech. 536, 49–78.CrossRefGoogle Scholar
Necker, F., Härtel, C., Kleiser, L. & Meiburg, E. 2005 Mixing and dissipation in particle-driven gravity currents. J. Fluid Mech. 545, 339–372.CrossRefGoogle Scholar
Ottolenghi, L., Adduce, C., Inghilesi, R., Armenio, V. & Roman, F. 2016a Entrainment and mixing in unsteady gravity currents. J. Hydraul Res. 54 (5), 541–557.CrossRefGoogle Scholar
Ottolenghi, L., Adduce, C., Inghilesi, R., Roman, F. & Armenio, V. 2016b Mixing in lock-release gravity currents propagating up a slope. Phys. Fluids 28, 056604.CrossRefGoogle Scholar
Patterson, M., Simpson, J., Dalziel, S. & Van Heijst, G. 2006 Vortical motion in the head of an axisymmetric gravity current. Phys. Fluids 18 (4), 0046601.CrossRefGoogle Scholar
Ross, A. N., Dalziel, S. B. & Linden, P. F. 2006 Axisymmetric gravity currents on a cone. J. Fluid Mech. 565, 227–253.CrossRefGoogle Scholar
Rubino, A. & Brandt, P. 2003 Warm-core eddies studied by laboratory experiments and numerical modeling. J. Phys. Oceanogr. 33, 431–435.2.0.CO;2>CrossRefGoogle Scholar
Saunders, P. M. 1973 The instability of a baroclinic vortex. J. Phys. Oceanogr. 3, 61–65.2.0.CO;2>CrossRefGoogle Scholar
Shin, J., Dalziel, S. & Linden, P. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.CrossRefGoogle Scholar
Simpson, J. 1997 Gravity Currents, 2nd edn. Cambridge University Press.Google Scholar
Simpson, J. E. 1972 Effects of the lower boundary on the head of a gravity current. J. Fluid Mech. 53, 759–768.CrossRefGoogle Scholar
Stegner, A., Bouruet-Aubertot, P. & Pichon, T. 2004 Nonlinear adjustment of density fronts. Part 1. The Rossby scenario and the experimental reality. J. Fluid Mech. 502, 335–360.CrossRefGoogle Scholar
Sutyrin, G. 2006 A self-similar axisymmetric pulson in rotating stratified fluid. J. Fluid Mech. 560, 243–248.CrossRefGoogle Scholar
Ungarish, M. 1993 Hydrodynamics of Suspensions. Springer.CrossRefGoogle Scholar
Ungarish, M. 2007 Axisymmetric gravity currents at high Reynolds number – on the quality of shallow-water modeling of experimental observations. Phys. Fluids 19, 036602.CrossRefGoogle Scholar
Ungarish, M. 2009 An Introduction to Gravity Currents and Intrusions. Chapman & Hall/CRC Press.CrossRefGoogle Scholar
Ungarish, M. 2010 The propagation of high-Reynolds-number non-Boussinesq gravity currents in axisymmetric geometry. J. Fluid Mech. 643, 267–277.CrossRefGoogle Scholar
Ungarish, M. & Huppert, H. E. 1998 The effects of rotation on axisymmetric gravity currents. J. Fluid Mech. 362, 17–51.CrossRefGoogle Scholar
Ungarish, M. & Huppert, H. E. 1999 Simple models of coriolis-influenced axisymmetric particle-driven gravity currents. Intl J. Multiphase Flow 25, 715–737.CrossRefGoogle Scholar
Ungarish, M. & Huppert, H. E. 2008 Energy balances for axisymmetric gravity currents in homogeneous and linearly stratified ambients. J. Fluid Mech. 616, 303–326.CrossRefGoogle Scholar
Ungarish, M. & Zemach, T. 2005 On the slumping of high Reynolds number gravity currents in two-dimensional and axisymmetric configurations. Eur. J. Mech. (B/Fluids) 24B, 71–90.CrossRefGoogle Scholar
Williamson, J. H. 1980 Low-storage Runge–Kutta schemes. J. Comput. Phys. 35, 48–56.CrossRefGoogle Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 418, 115–128.CrossRefGoogle Scholar