Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T09:22:05.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluctuations of thermodynamic variables in stationary compressible turbulence

Published online by Cambridge University Press:  23 September 2013

Diego A. Donzis  and
Shriram Jagannathan
Diego A. Donzis*
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 12345, USA
Shriram Jagannathan
Affiliation:
Department of Aerospace Engineering, Texas A&M University, College Station, TX 12345, USA
*
†Email address for correspondence: donzis@tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

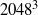A large database of new direct numerical simulations of forced compressible turbulence on up to $204{8}^{3} $ grids, and a range of Reynolds (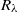${R}_{\lambda } $) and turbulent Mach (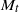${M}_{t} $) numbers, is analysed to study the scaling of pressure, density and temperature fluctuations. Small-perturbation analysis is used to study the scaling of variances, and different cross-correlations as well as spectra. Qualitative differences are observed between low and high 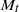${M}_{t} $. The probability density functions (p.d.f.s) of pressure and density are negatively skewed at low 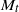${M}_{t} $ (consistent with incompressible results) but become positively skewed at high 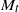${M}_{t} $. The positive tails are found to follow a log-normal distribution. A new variable is introduced to quantify departures from isentropic fluctuations (an assumption commonly used in the literature) and is found to increase as 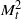${ M}_{t}^{2} $. However, positive fluctuations of pressure and density tend to be more isentropic than negative fluctuations. In general, Reynolds number effects on single-point statistics are observed to be weak. The spectral behaviour of pressure, density and temperature is also investigated. While at low 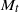${M}_{t} $, pressure appears to scale as 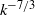${k}^{- 7/ 3} $ (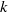$k$ is the wavenumber) in the inertial range as in incompressible flows, a 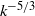${k}^{- 5/ 3} $ scaling also appears to be consistent with the data at a range of Mach numbers. Density and temperature spectra are found to scale as 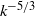${k}^{- 5/ 3} $ for a range of Mach numbers.

JFM classification

Turbulent Flows: Compressible turbulence Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 221 - 244
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayly, B. J., Levermore, C. D. & Passot, T. 1992 Density variations in weakly compressible flows. Phys. Fluids 4, 945–954.CrossRefGoogle Scholar
Beetz, C., Schwarz, C., Dreher, J. & Grauer, R. 2008 Density-PDFs and Lagrangian statistics of highly compressible turbulence. Phys. Lett. A 372, 3037–3041.CrossRefGoogle Scholar
Biskamp, D. 2003 Magnetohydrodynamic Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Blaisdell, G. A., Mansour, N. N. & Reynolds, W. C. 1993 Compressibility effects on the growth and structure of homogeneous turbulent shear flow. J. Fluid Mech. 256, 443–485.CrossRefGoogle Scholar
Cao, N. Z., Chen, S. Y. & Doolen, G. D. 1999 Statistics and structures of pressure in isotropic turbulence. Phys. Fluids 11, 2235–2250.CrossRefGoogle Scholar
Chandrasekhar, S. 1951 The fluctuations of density in isotropic turbulence. Proc. R. Soc. Lond. A 210 (1100), 18–25.Google Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22, 469–473.CrossRefGoogle Scholar
Dastgeer, S. & Zank, G. P. 2005 Turbulence in nearly incompressible fluids: density spectrum, flows, correlations and implication to the interstellar medium. Nonlinear Proc. Geophys. 12, 139–148.CrossRefGoogle Scholar
Denbigh, K. 1981 The Principles of Chemical Equilibrium. Cambridge University Press.CrossRefGoogle Scholar
Donzis, D. A. & Sreenivasan, K. R. 2010 The bottleneck effect and the Kolmogorov constant in isotropic turbulence. J. Fluid Mech. 657, 171–188.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2010 The Batchelor spectrum for mixing of passive scalars in isotropic turbulence. Flow Turbul. Combust. 85, 549–566.CrossRefGoogle Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2012 Some results on the Reynolds number scaling of pressure statistics in isotropic turbulence. Physica D 241, 164–168.CrossRefGoogle Scholar
Erlebacher, G., Hussaini, M. Y., Kreiss, H. O. & Sarkar, S. 1990 The analysis and simulation of compressible turbulence. Theor. Comput. Fluid Dyn. 2, 73–95.CrossRefGoogle Scholar
Eswaran, V. & Pope, S. B. 1988 An examination of forcing in direct numerical simulations of turbulence. Comput. Fluids 16, 257–278.CrossRefGoogle Scholar
Federrath, C., Klessen, R. S. & Schmidt, W. 2008 The density probability distribution in compressible isothermal turbulence: solenoidal versus compressive forcing. Astrophys. J. Lett. 688, L79–L82.CrossRefGoogle Scholar
Feller, W. 1971 An Introduction to Probability Theory and its Applications. Wiley.Google Scholar
Gotoh, T. & Fukayama, D. 2001 Pressure spectrum in homogeneous turbulence. Phys. Rev. Lett. 86, 3775–3778.CrossRefGoogle ScholarPubMed
Gotoh, T. & Rogallo, R. S. 1999 Intermittency and scaling of pressure at small scales in forced isotropic turbulence. J. Fluid Mech. 396, 257–285.CrossRefGoogle Scholar
Hunana, P. & Zank, G. P. 2010 Inhomogeneous nearly incompressible description of magnetohydrodynamic turbulence. Astrophys. J. 718, 148–167.CrossRefGoogle Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Jagannathan, S. & Donzis, D. A. 2012 Massively parallel direct numerical simulations of forced compressible turbulence: a hybrid MPI/OpenMP approach. In Proceedings of the 1st Conference of the Extreme Science and Engineering Discovery Environment, p. 23.Google Scholar
Kida, S. & Orszag, S. A. 1990 Energy and spectral dynamics in forced compressible turbulence. J. Sci. Comp. 5, 85–125.CrossRefGoogle Scholar
Kida, S. & Orszag, S. A. 1992 Energy and spectral dynamics in decaying compressible turbulence. J. Sci. Comp. 7, 1–34.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kraichnan, R. H. 1953 The scattering of sound in a turbulent medium. J. Acoust. Soc. Am. 25, 1096–1104.CrossRefGoogle Scholar
Lee, S. K., Benaissa, A., Djenidi, L., Lavoie, P. & Antonia, R. A. 2012 Scaling range of velocity and passive scalar spectra in grid turbulence. Phys. Fluids 24, 075101.CrossRefGoogle Scholar
Lee, K. & Girimaji, S. 2011 Flow–thermodynamics interactions in decaying anisotropic compressible turbulence with imposed temperature fluctuations. In Theor. Comput. Fluid Dyn., pp. 1–17.Google Scholar
Lee, S., Lele, S. K. & Moin, P. 1991 Eddy shocklets in decaying compressible turbulence. Phys. Fluids 3, 657–664.CrossRefGoogle Scholar
Lele, S. K. 1994 Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 26, 211–254.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. II, MIT.Google Scholar
Montgomery, D., Brown, M. R. & Matthaeus, W. H. 1987 Density fluctuation spectra in magnetohydrodynamic turbulence. J. Geophys. Res. 92, 282–284.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1998 Passive scalar statistics in high-Peclet-number grid turbulence. J. Fluid Mech. 358, 135–175.CrossRefGoogle Scholar
Obukhov, A. M. 1949 The structure of the temperature field in a turbulent flow. Izv. Akad. Nauk SSSR 13, 58–69.Google Scholar
Padoan, P., Jones, B. J. T. & Nordlund, A. P. 1997 Supersonic turbulence in the interstellar medium: stellar extinction determinations as probes of the structure and dynamics of dark clouds. Astrophys. J. 474, 730–734.CrossRefGoogle Scholar
Papoulis, A. & Pillai, S. U. 2002 Probability, Random Variables and Stochastic Processes, 4th edn. McGraw-Hill.Google Scholar
Petersen, M. R. & Livescu, D. 2010 Forcing for statistically stationary compressible isotropic turbulence. Phys. Fluids 22, 116101.CrossRefGoogle Scholar
Pirozzoli, S. 2011 Numerical methods for high-speed flows. Annu. Rev. Fluid Mech. 43, 163–194.CrossRefGoogle Scholar
Pirozzoli, S. & Grasso, F. 2004 Direct numerical simulations of isotropic compressible turbulence: influence of compressibility on dynamics and structures. Phys. Fluids 16, 4386–4407.CrossRefGoogle Scholar
Pumir, A. 1994 A numerical study of pressure-fluctuations in three-dimensional, incompressible, homogeneous, isotropic turbulence. Phys. Fluids 6, 2071–2083.CrossRefGoogle Scholar
Rubesin, M. W. 1976 A one-equation model of turbulence for use with the compressible Navier–Stokes equations. NASA Tech. Memo. X–73128.Google Scholar
Samtaney, R., Pullin, D. I. & Kosovic, B. 2001 Direct numerical simulation of decaying compressible turbulence and shocklet statistics. Phys. Fluids 13, 1415–1430.CrossRefGoogle Scholar
Sarkar, S., Erlebacher, G., Hussaini, M. Y. & Kreiss, H. O. 1991 The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 227, 473–493.CrossRefGoogle Scholar
Scalo, J., Vázquez-Semadeni, E., Chappell, D. & Passot, T. 1998 On the probability density function of galactic gas. Part 1. Numerical simulations and the significance of the polytropic index. Astrophys. J. 504, 835–853.CrossRefGoogle Scholar
Smits, A. J. & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer.Google Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the Obukhov–Corrsin constant. Phys. Fluids 8, 189–196.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Tsuji, Y. & Ishihara, T. 2003 Similarity scaling of pressure fluctuation in turbulence. Phys. Rev. E 68, 026309.CrossRefGoogle ScholarPubMed
Vedula, P. & Yeung, P. K. 1999 Similarity scaling of acceleration and pressure statistics in numerical simulations of isotropic turbulence. Phys. Fluids 11, 1208–1220.CrossRefGoogle Scholar
Wang, J., Shi, Y., Wang, L.-P., Xiao, Z., He, X. & Chen, S. 2011 Effect of shocklets on the velocity gradients in highly compressible isotropic turbulence. Phys. Fluids 23, 125103.CrossRefGoogle Scholar
Wang, J., Shi, Y., Wang, L.-P., Xiao, Z., He, X. T. & Chen, S. 2012 Effect of compressibility on the small-scale structures in isotropic turbulence. J. Fluid Mech. 713, 588–631.CrossRefGoogle Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2004 Statistics of a passive scalar in homogeneous turbulence. New J. Phys. 6, 40.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2007 Inertial-range intermittency and accuracy of direct numerical simulation for turbulence and passive scalar turbulence. J. Fluid Mech. 590, 117–146.CrossRefGoogle Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2005 High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 17, 081703.CrossRefGoogle Scholar