Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Huang, Y. X.
Schmitt, F. G.
Zhou, Q.
Qiu, X.
Shang, X. D.
Lu, Z. M.
and
Liu, Y. L.
2011.
Scaling of maximum probability density functions of velocity and temperature increments in turbulent systems.
Physics of Fluids,
Vol. 23,
Issue. 12,
Zhou, Quan
and
Xia, Ke-Qing
2011.
Disentangle plume-induced anisotropy in the velocity field in buoyancy-driven turbulence.
Journal of Fluid Mechanics,
Vol. 684,
Issue. ,
p.
192.
Guo, Li
Li, Dong
Zhang, Xing
and
He, Guo-Wei
2012.
LES prediction of space-time correlations in turbulent shear flows.
Acta Mechanica Sinica,
Vol. 28,
Issue. 4,
p.
993.
He, Xiaozhou
Funfschilling, Denis
Nobach, Holger
Bodenschatz, Eberhard
and
Ahlers, Guenter
2012.
Transition to the Ultimate State of Turbulent Rayleigh-Bénard Convection.
Physical Review Letters,
Vol. 108,
Issue. 2,
Zhou, Quan
and
Xia, Ke-Qing
2013.
Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell.
Journal of Fluid Mechanics,
Vol. 721,
Issue. ,
p.
199.
Stevens, Richard J. A. M.
van der Poel, Erwin P.
Grossmann, Siegfried
and
Lohse, Detlef
2013.
The unifying theory of scaling in thermal convection: the updated prefactors.
Journal of Fluid Mechanics,
Vol. 730,
Issue. ,
p.
295.
Guo, Hao
Li, Chao
Qu, QiuLin
and
Liu, PeiQing
2013.
Attractive fixed-point solution study of a shell model for turbulent convection.
Science China Physics, Mechanics and Astronomy,
Vol. 56,
Issue. 5,
p.
995.
Skvortsov, Alex
Jamriska, Milan
and
DuBois, Timothy C.
2013.
Tracer Dispersion in the Turbulent Convective Layer.
Journal of the Atmospheric Sciences,
Vol. 70,
Issue. 12,
p.
4112.
Hogg, James
and
Ahlers, Guenter
2013.
Reynolds-number measurements for low-Prandtl-number turbulent convection of large-aspect-ratio samples.
Journal of Fluid Mechanics,
Vol. 725,
Issue. ,
p.
664.
Xia, Ke-Qing
2013.
Current trends and future directions in turbulent thermal convection.
Theoretical and Applied Mechanics Letters,
Vol. 3,
Issue. 5,
p.
052001.
Wang, Wei
Guan, Xin-Lei
and
Jiang, Nan
2014.
TRPIV investigation of space-time correlation in turbulent flows over flat and wavy walls.
Acta Mechanica Sinica,
Vol. 30,
Issue. 4,
p.
468.
He, Xiaozhou
van Gils, Dennis P. M.
Bodenschatz, Eberhard
and
Ahlers, Guenter
2014.
Logarithmic Spatial Variations and Universalf−1Power Spectra of Temperature Fluctuations in Turbulent Rayleigh-Bénard Convection.
Physical Review Letters,
Vol. 112,
Issue. 17,
Wang, Wei
Guan, Xin-Lei
and
Jiang, Nan
2014.
Convection and correlation of coherent structure in turbulent boundary layer using tomographic particle image velocimetry.
Chinese Physics B,
Vol. 23,
Issue. 10,
p.
104703.
Qiu, Xiang
Huang, Yong-xiang
Zhou, Quan
and
Sun, Chao
2014.
Scaling of maximum probability density function of velocity increments in turbulent Rayleigh-Bénard convection.
Journal of Hydrodynamics,
Vol. 26,
Issue. 3,
p.
351.
He, Xiaozhou
and
Tong, Penger
2014.
Space-time correlations in turbulent Rayleigh-Bénard convection.
Acta Mechanica Sinica,
Vol. 30,
Issue. 4,
p.
457.
He, Xiaozhou
Shang, Xiao-dong
and
Tong, Penger
2014.
Test of the anomalous scaling of passive temperature fluctuations in turbulent Rayleigh–Bénard convection with spatial inhomogeneity.
Journal of Fluid Mechanics,
Vol. 753,
Issue. ,
p.
104.
He, Xiaozhou
Gils, Dennis P M van
Bodenschatz, Eberhard
and
Ahlers, Guenter
2015.
Reynolds numbers and the elliptic approximation near the ultimate state of turbulent Rayleigh–Bénard convection.
New Journal of Physics,
Vol. 17,
Issue. 6,
p.
063028.
McManus, Thomas A.
and
Sutton, Jeffrey A.
2015.
Large Scale Dynamics and Statistics of the Time-Varying Temperature Field in Turbulent Non-Premixed Jet Flames.
Geng, Chenhui
He, Guowei
Wang, Yinshan
Xu, Chunxiao
Lozano-Durán, Adrián
and
Wallace, James M.
2015.
Taylor’s hypothesis in turbulent channel flow considered using a transport equation analysis.
Physics of Fluids,
Vol. 27,
Issue. 2,
Hoefnagels, Paul B. J.
Wei, Ping
Narezo Guzman, Daniela
Sun, Chao
Lohse, Detlef
and
Ahlers, Guenter
2017.
Large-scale flow and Reynolds numbers in the presence of boiling in locally heated turbulent convection.
Physical Review Fluids,
Vol. 2,
Issue. 7,
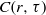 , in a cylindrical turbulent Rayleigh–Bénard convection cell using the particle image velocimetry (PIV) technique. We show that while Taylor’s frozen-flow hypothesis does not hold in turbulent thermal convection, the recent elliptic model advanced for turbulent shear flows (He & Zhang, Phys. Rev. E, vol. 73, 055303) is valid for the present velocity field for all over the cell, i.e. the isocorrelation contours of the measured
, in a cylindrical turbulent Rayleigh–Bénard convection cell using the particle image velocimetry (PIV) technique. We show that while Taylor’s frozen-flow hypothesis does not hold in turbulent thermal convection, the recent elliptic model advanced for turbulent shear flows (He & Zhang, Phys. Rev. E, vol. 73, 055303) is valid for the present velocity field for all over the cell, i.e. the isocorrelation contours of the measured 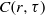 have an elliptical curve shape and hence
have an elliptical curve shape and hence 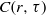 can be related to
can be related to 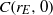 via
via 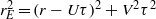 with
with 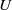 and
and 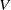 being two characteristic velocities. We further show that the fitted
being two characteristic velocities. We further show that the fitted 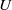 is proportional to the mean velocity of the flow, but the values of
is proportional to the mean velocity of the flow, but the values of 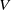 are larger than the theoretical predictions. Specifically, we focus on two representative regions in the cell: the region near the cell sidewall and the cell’s central region. It is found that
are larger than the theoretical predictions. Specifically, we focus on two representative regions in the cell: the region near the cell sidewall and the cell’s central region. It is found that 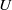 and
and 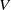 are approximately the same near the sidewall, while
are approximately the same near the sidewall, while 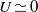 at the cell centre.
at the cell centre.