Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-24T08:37:26.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Equilibria and stabilities of a confined floating cylinder

Published online by Cambridge University Press:  03 January 2023

Wanqiu Zhang Open the ORCID record for Wanqiu Zhang [Opens in a new window]  and
Xinping Zhou Open the ORCID record for Xinping Zhou [Opens in a new window]
Wanqiu Zhang
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China
Xinping Zhou*
Affiliation:
School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, PR China State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, PR China
*
†Email address for correspondence: xpzhou08@hust.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

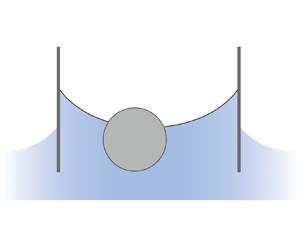
A two-dimensional system with a floating cylinder confined between two parallel vertical stationary plates partially immersed in an infinite liquid bath in a downward gravity field is considered. The equilibrium states of the system are investigated using the Young–Laplace equation in two dimensions. According to the symmetry of menisci at both sides of the cylinder, the equilibrium states are classified into three types: the equilibria of fully symmetric menisci, the equilibria of partially symmetric menisci and the equilibria of asymmetric menisci. The study is then extended to investigate the stabilities of the confined cylinder with bifurcation theory. Results show that there can be at most two stable regions in the bifurcation diagram. For different plates’ contact angles, there are five representative types of bifurcation behaviours for either the case of one stable region or the case of two stable regions. In comparison with the case of an unconfined cylinder, the confinement by two hydrophobic plates with a small spacing can assist the stable interfacial floatation of the confined cylinder with a large weight.

JFM classification

Interfacial Flows (free surface): Capillary flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 954 , 10 January 2023 , A22
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aspley, A., He, C. & Mccuan, J. 2015 Force profiles for parallel plates partially immersed in a liquid bath. J. Math. Fluid Mech. 17, 87–102.CrossRefGoogle Scholar
Basualdo, F.N.P., Bolopion, A., Gauthier, M. & Lambert, P. 2021 A microrobotic platform actuated by thermocapillary flows for manipulation at the air-water interface. Sci. Robot. 6, eabd3557.CrossRefGoogle Scholar
Benilov, E.S. & Oron, A. 2010 The height of a static liquid column pulled out of an infinite pool. Phys. Fluids 22, 102101.CrossRefGoogle Scholar
Bhatnagar, R. & Finn, R. 2006 Equilibrium configurations of an infinite cylinder in an unbounded fluid. Phys. Fluids 18, 047103.CrossRefGoogle Scholar
Bhatnagar, R. & Finn, R. 2013 Attractions and repulsions of parallel plates partially immersed in a liquid bath: III. Bound. Value Probl. 2013, 277.CrossRefGoogle Scholar
Bhatnagar, R. & Finn, R. 2016 a On the capillarity equation in two dimensions. J. Math. Fluid Mech. 18, 731–738.CrossRefGoogle Scholar
Bhatnagar, R. & Finn, R. 2016 b The force singularity for partially immersed parallel plates. J. Math. Fluid Mech. 18, 739–755.CrossRefGoogle Scholar
Biran, A. 2003 Basic ship hydrostatics. In Ship Hydrostatics and Stability, pp. 23–70. Butterworth-Heinemann.CrossRefGoogle Scholar
Bowden, N., Terfort, A., Carbeck, J. & Whitesides, G.M. 1997 Self-assembly of mesoscale objects into ordered two-dimensional arrays. Science 276, 233–235.CrossRefGoogle ScholarPubMed
Bullard, J.W. & Garboczi, E.J. 2009 Capillary rise between planar surfaces. Phys. Rev. E 79, 011604.CrossRefGoogle ScholarPubMed
Bush, J.W.M. & Hu, D.L. 2006 Walking on water: biolocomotion at the interface. Annu. Rev. Fluid Mech. 38, 339–369.CrossRefGoogle Scholar
Chen, H. & Siegel, D. 2018 A floating cylinder on an unbounded bath. J. Math. Fluid Mech. 20, 1373–1404.CrossRefGoogle Scholar
Concus, P. 1968 Static menisci in a vertical right circular cylinder. J. Fluid Mech. 34, 481–495.CrossRefGoogle Scholar
Concus, P. & Finn, R. 1991 Exotic containers for capillary surfaces. J. Fluid Mech. 224, 383–394.CrossRefGoogle Scholar
Concus, P., Finn, R. & Weislogel, M. 1999 Capillary surfaces in an exotic container: results from space experiments. J. Fluid Mech. 394, 119–135.CrossRefGoogle Scholar
Erdös, P., Schibler, G. & Herndon, R. 1992 a Floating equilibrium of symmetrical objects and the breaking of symmetry. Part 1: prisms. Am. J. Phys. 60, 335–345.CrossRefGoogle Scholar
Erdös, P., Schibler, G. & Herndon, R. 1992 b Floating equilibrium of symmetrical objects and the breaking of symmetry. Part 2: the cube, the octahedron, and the tetrahedron. Am. J. Phys. 60, 345–356.CrossRefGoogle Scholar
Finn, R. 1986 Equilibrium Capillary Surfaces. Springer.CrossRefGoogle Scholar
Finn, R. 2006 The contact angle in capillarity. Phys. Fluids 18, 047102.CrossRefGoogle Scholar
Finn, R. 2010 On Young's Paradox, and the attractions of immersed parallel plates. Phys. Fluids 22, 017103.CrossRefGoogle Scholar
Finn, R. 2013 Capillary forces on partially immersed plates. In Differential and Difference Equations with Applications, pp. 13–25. Springer.CrossRefGoogle Scholar
Finn, R. & Lu, D. 2013 Mutual attractions of partially immersed parallel plates. J. Math. Fluid Mech. 15, 273–301.CrossRefGoogle Scholar
Forsythe, G.E., Moler, C.B. & Malcolm, M.A. 1977 Solution of nonlinear equations. In Computer Methods for Mathematical Computations, pp. 156–171. Prentice Hall.Google Scholar
Hand, L. & Finch, J. 1998 Analytical Mechanics. Cambridge University Press.CrossRefGoogle Scholar
Ho, I., Pucci, G. & Harris, D.M. 2019 Direct measurement of capillary attraction between floating disks. Phys. Rev. Lett. 123, 254502.CrossRefGoogle ScholarPubMed
Hu, W., Lum, G.Z., Mastrangeli, M. & Sitti, M. 2018 Small-scale soft-bodied robot with multimodal locomotion. Nature 554, 81–85.CrossRefGoogle ScholarPubMed
Janssens, S., Chaurasia, V. & Fried, E. 2017 Effect of a surface tension imbalance on a partly submerged cylinder. J. Fluid Mech. 830, 369–386.CrossRefGoogle Scholar
Karasslanli, C.C. 2012 Bifurcation analysis and its application. Chapter 1. In Numerical Simulation: From Theory to Industry (ed. M. Andriychuk). INTECH.Google Scholar
Keller, J.B. 1998 Surface tension force on a partly submerged body. Phys. Fluids 10, 3009–3010.CrossRefGoogle Scholar
Kralchevsky, P.A., Paunov, V.N., Denkov, N.D., Ivanov, I.B. & Nagayama, K. 1993 Energetical and force approaches to the capillary interactions between particles attached to a liquid–fluid interface. J. Colloid Interface Sci. 155, 420–437.CrossRefGoogle Scholar
Majumdar, S.R. & Michael, D.H. 1976 The equilibrium and stability of two dimensional pendent drops. Proc. R. Soc. Lond. Ser. A-Math. Phys. Engng Sci. 351, 89–115.Google Scholar
Mccuan, J. & Treinen, R. 2013 Capillarity and Archimedes’ principle. Pac. J. Maths 265, 123–150.CrossRefGoogle Scholar
Mccuan, J. & Treinen, R. 2018 On floating equilibria in a laterally finite container. SIAM J. Appl. Maths 78, 551–570.CrossRefGoogle Scholar
Padday, J.F. 1971 The profiles of axially symmetric menisci. Phil. Trans. R. Soc. Lond. Ser. A-Math. Phys. Engng Sci. 269, 265–293.Google Scholar
Seydel, R. 2009 Practical Bifurcation and Stability Analysis, Vol. 5. Springer Science & Business Media.Google Scholar
Singh, P. & Hesla, T.I. 2004 The interfacial torque on a partially submerged sphere. J. Colloid Interface Sci. 280, 542–543.CrossRefGoogle ScholarPubMed
Vella, D. 2015 Floating versus sinking. Annu. Rev. Fluid Mech. 47, 115–135.CrossRefGoogle Scholar
Wente, H.C. 2011 Exotic capillary tubes. J. Math. Fluid Mech. 13, 355–370.CrossRefGoogle Scholar
Zhang, F. & Zhou, X. 2020 General exotic capillary tubes. J. Fluid Mech. 885, A1.CrossRefGoogle Scholar
Zhang, F., Zhou, X. & Zhu, C. 2018 Effects of surface tension on a floating body in two dimensions. J. Fluid Mech. 847, 489–519.CrossRefGoogle Scholar
Zhou, X. & Zhang, F. 2017 Bifurcation of a partially immersed plate between two parallel plates. J. Fluid Mech. 817, 122–137.CrossRefGoogle Scholar