Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-16T15:48:29.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Ellipsoidal vortices in rotating stratified fluids: beyond the quasi-geostrophic approximation

Published online by Cambridge University Press:  02 December 2014

Yue-Kin Tsang Open the ORCID record for Yue-Kin Tsang [Opens in a new window]  and
David G. Dritschel
Yue-Kin Tsang*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
David G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Present address: School of Mathematics, University of Edinburgh, Edinburgh EH9 3JZ, UK. Email address for correspondence: yktsang@ed.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the basic properties and stability of isolated vortices having uniform potential vorticity (PV) in a non-hydrostatic rotating stratified fluid, under the Boussinesq approximation. For simplicity, we consider a uniform background rotation and a linear basic-state stratification for which both the Coriolis and buoyancy frequencies, 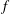$f$ and 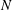$N$, are constant. Moreover, we take 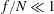$f/N\ll 1$, as typically observed in the Earth’s atmosphere and oceans. In the small Rossby number ‘quasi-geostrophic’ (QG) limit, when the flow is weak compared to the background rotation, there exist exact solutions for steadily rotating ellipsoidal volumes of uniform PV in an unbounded flow (Zhmur & Shchepetkin, Izv. Akad. Nauk SSSR Atmos. Ocean. Phys., vol. 27, 1991, pp. 492–503; Meacham, Dyn. Atmos. Oceans, vol. 16, 1992, pp. 189–223). Furthermore, a wide range of these solutions are stable as long as the horizontal and vertical aspect ratios 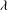${\it\lambda}$ and 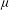${\it\mu}$ do not depart greatly from unity (Dritschel et al.,J. Fluid Mech., vol. 536, 2005, pp. 401–421). In the present study, we examine the behaviour of ellipsoidal vortices at Rossby numbers up to near unity in magnitude. We find that there is a monotonic increase in stability as one varies the Rossby number from nearly 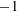$-1$ (anticyclone) to nearly 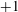$+1$ (cyclone). That is, QG vortices are more stable than anticyclones at finite negative Rossby number, and generally less stable than cyclones at finite positive Rossby number. Ageostrophic effects strengthen both the rotation and the stratification within a cyclone, enhancing its stability. The converse is true for an anticyclone. For all Rossby numbers, stability is reinforced by increasing 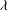${\it\lambda}$ towards unity or decreasing 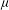${\it\mu}$. An unstable vortex often restabilises by developing a near-circular cross-section, typically resulting in a roughly ellipsoidal vortex, but occasionally a binary system is formed. Throughout the nonlinear evolution of a vortex, the emission of inertia–gravity waves (IGWs) is negligible across the entire parameter space investigated. Thus, vortices at small to moderate Rossby numbers, and any associated instabilities, are (ageostrophically) balanced. A manifestation of this balance is that, at finite Rossby number, an anticyclone rotates faster than a cyclone.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 196 - 231
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carlson, B. C. & Gustafson, J. L. 1994 Asymptotic approximations for symmetric elliptic integrals. SIAM J. Math. Anal. 25, 288–303.CrossRefGoogle Scholar
Carton, X. 2001 Hydrodynamical modelling of oceanic vortices. Surv. Geophys. 22, 179–263.CrossRefGoogle Scholar
Carton, X. 2010 Oceanic vortices. In Fronts, Waves and Vortices in Geophysical Flows (ed. Flor, J.-B.), Lecture Notes in Physics, vol. 805, chap. 3, pp. 61–108. Springer.CrossRefGoogle Scholar
Chandrasekhar, S. 1987 Ellipsoid Figures of Equilibrium. Dover.Google Scholar
Charney, J. G. 1948 On the scale of atmospheric motions. Geofys. Publ. Oslo 17, 1–17.Google Scholar
Chelton, D. B., Schlax, M. G. & Samelson, R. M. 2011 Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 111, 167–216.CrossRefGoogle Scholar
Cushman-Roisin, B. 1986 Linear stability of large, elliptical warm-core rings. J. Phys. Oceanogr. 16, 1158–1164.2.0.CO;2>CrossRefGoogle Scholar
Cushman-Roisin, B., Heil, W. H. & Nof, D. 1985 Oscillations and rotations of elliptical warm-core rings. J. Geophys. Res. 90, 11756–11764.CrossRefGoogle Scholar
Dritschel, D. G. 1990 The stability of elliptical vortices in an external straining flow. J. Fluid Mech. 210, 223–261.CrossRefGoogle Scholar
Dritschel, D. G. & Ambaum, M. H. P. 1997 A contour-advective semi-Lagrangian numerical algorithm for simulating fine-scale conservative dynamical fields. Q. J. R. Meteorol. Soc. 123, 1097–1130.Google Scholar
Dritschel, D. G. & McKiver, W. J.2014 Effect of Prandtl’s ratio on balance in geophysical turbulence, J. Fluid Mech. (submitted).CrossRefGoogle Scholar
Dritschel, D. G., Scott, R. K. & Reinaud, J. N. 2005 The stability of quasi-geostrophic ellipsoid vortices. J. Fluid Mech. 536, 401–421.CrossRefGoogle Scholar
Dritschel, D. G. & Viúdez, Á. 2003 A balanced approach to modelling rotating stably stratified geophysical flows. J. Fluid Mech. 488, 123–150.CrossRefGoogle Scholar
Dritschel, D. G. & Viúdez, Á. 2007 The persistence of balance in geophysical flows. J. Fluid Mech. 570, 365–383.CrossRefGoogle Scholar
Fontane, J. & Dritschel, D. G. 2009 The HyperCASL algorithm: a new approach to the numerical simulation of geophysical flows. J. Comput. Phys. 228, 6411–6425.CrossRefGoogle Scholar
Ford, R., McIntyre, M. E. & Norton, W. A. 2000 Balance and the slow quasimanifold: some explicit results. J. Atmos. Sci. 57, 1236–1254.2.0.CO;2>CrossRefGoogle Scholar
Hashimoto, H., Shimonishi, T. & Miyazaki, T. 1999 Quasigeostrophic, ellipsoidal vortices in a two-dimensional strain field. J. Phys. Soc. Japan 68 (12), 3863–3880.CrossRefGoogle Scholar
Hebert, D., Oakey, N. & Ruddick, B. 1990 Evolution of a Mediterranean salt lens: scalar properties. J. Phys. Oceanogr. 20, 1468–1483.2.0.CO;2>CrossRefGoogle Scholar
Hoskins, B. J., McIntyre, M. E. & Robertson, A. W. 1985 On the use and significance of isentropic potential-vorticity maps. Q. J. R. Meteorol. Soc. 111, 877–946.CrossRefGoogle Scholar
Hou, T. Y. & Li, R. 2007 Computing nearly singular solutions using pseudo-spectral methods. J. Comput. Phys. 226, 379–397.CrossRefGoogle Scholar
Kida, S. 1981 Motion of an elliptic vortex in a uniform shear flow. J. Phys. Soc. Japan 50 (10), 3517–3520.CrossRefGoogle Scholar
Kim, S. Y. 2010 Observations of submesoscale eddies using high-frequency radar-derived kinematic and dynamic quantities. Cont. Shelf Res. 30 (15), 1639–1655.CrossRefGoogle Scholar
Kirchhoff, G. 1876 Vorlesungen über Mathematische Physik: Mechanik. Teubner.Google Scholar
Lamb, S. H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Lentini, C. A. D., Goni, G. J. & Olson, D. B. 2006 Investigation of Brazil Current rings in the confluence region. J. Geophys. Res. Oceans 111, 2156–2202.CrossRefGoogle Scholar
McDowell, S. E. & Rossby, H. T. 1978 Mediterranean water: an intense mesoscale eddy off the Bahamas. Science 202, 1085–1087.Google Scholar
McKiver, W. J. & Dritschel, D. G. 2003 The motion of a fluid ellipsoid vortex in a general linear background flow. J. Fluid Mech. 474, 147–173.CrossRefGoogle Scholar
McKiver, W. J. & Dritschel, D. G. 2006 The stability of a quasi-geostrophic ellipsoid vortex in a background strain flow. J. Fluid Mech. 560, 1–17.CrossRefGoogle Scholar
McKiver, W. J. & Dritschel, D. G. 2008 Balance in non-hydrostatic rotating stratified turbulence. J. Fluid Mech. 596, 201–219.CrossRefGoogle Scholar
Meacham, S. P. 1992 Quasigeostrophic, ellipsoidal vortices in a stratified flow. Dyn. Atmos. Oceans 16, 189–223.CrossRefGoogle Scholar
Meacham, S. P., Flirel, G. R. & Send, U. 1990 Vortices in shear. Dyn. Atmos. Oceans 14, 333–386.CrossRefGoogle Scholar
Meacham, S. P., Morrison, P. J. & Flirel, G. R. 1997 Hamiltonian moment reduction for describing vortices in shear. Phys. Fluids 9 (8), 2310–2328.CrossRefGoogle Scholar
Meacham, S. P., Pankratov, K. K., Shchepetkin, A. F. & Zhmur, V. V. 1994 The interaction of ellipsoidal vortices with background shear flows in a stratified fluid. Dyn. Atmos. Oceans 21, 167–212.CrossRefGoogle Scholar
Meleshko, V. V. & van Heijst, G. J. F. 1994 On Chaplygin’s investigations of two-dimensional vortex structures in an inviscid fluid. J. Fluid Mech. 272, 157–182.CrossRefGoogle Scholar
Miyazaki, T., Ueno, K. & Shimonishi, T. 1999 Quasigeostrophic, tilted spheroidal vortices. J. Phys. Soc. Japan 68 (8), 2592–2601.CrossRefGoogle Scholar
Mohebalhojeh, A. R. & Dritschel, D. G. 2001 Hierarchies of balance conditions for the $f$ -plane shallow water equations. J. Atmos. Sci. 58 (16), 2411–2426.2.0.CO;2>CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1971 Aircraft Wake Turbulence and its Detection, p. 339. Plenum.CrossRefGoogle Scholar
Muraki, D. J., Snyder, C. & Rotunno, R. 1999 The next-order corrections to quasigeostrophic theory. J. Atmos. Sci. 56, 1547–1560.2.0.CO;2>CrossRefGoogle Scholar
Ólafsdóttir, E. I., Olde Daalhuis, A. B. & Vanneste, J. 2008 Inertia-gravity-wave radiation by a sheared vortex. J. Fluid Mech. 596, 169–189.CrossRefGoogle Scholar
Olson, D. B. 1991 Rings in the ocean. Annu. Rev. Earth Planet. Sci. 19, 283–311.CrossRefGoogle Scholar
Paillet, J., Le Cann, R., Carton, X., Morel, Y. & Serpette, A. 2002 Dynamics and evolution of a northern meddy. J. Phys. Oceanogr. 32, 55–79.2.0.CO;2>CrossRefGoogle Scholar
Park, K.-A., Woo, H.-J. & Ryu, J.-H. 2012 Spatial scales of mesoscale eddies from GOCI chlorophyll- ${\it\alpha}$ concentration images in the East/Japan Sea. Ocean Sci. J. 47 (3), 347–358.CrossRefGoogle Scholar
Płotka, H. & Dritschel, D. G. 2012 Quasi-geostrophic shallow-water vortex-patch equilibria and their stability. Geophys. Astrophys. Fluid Dyn. 106, 574–595.CrossRefGoogle Scholar
Płotka, H. & Dritschel, D. G. 2014 Simply-connected vortex-patch shallow-water quasi-equilibria. J. Fluid Mech. 743, 481–502.CrossRefGoogle Scholar
Prater, M. D. & Sanford, T. B. 1994 A meddy off Cape St. Vincent. Part I: description. J. Phys. Oceanogr. 24, 1572–1586.2.0.CO;2>CrossRefGoogle Scholar
Rankine, W. J. M. 1858 A Manual of Applied Mechanics. Griffin.Google Scholar
Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. J. Theor. Comput. Fluid Dyn. 11, 305–322.CrossRefGoogle Scholar
Spence, T. W. & Legeckis, R. 1981 Satellite and hydrographic observations of low-frequency wave motions associated with a cold core Gulf Stream ring. J. Geophys. Res. 86, 1945–1953.CrossRefGoogle Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Viúdez, Á. 2007 The origin of the stationary frontal wavepacket spontaneously generated in rotating stratified vortex dipoles. J. Fluid Mech. 593, 359–383.CrossRefGoogle Scholar
Viúdez, Á. & Dritschel, D. G. 2004 Optimal potential vorticity balance of geophysical flows. J. Fluid Mech. 521, 343–352.CrossRefGoogle Scholar
Warn, T., Bokhove, O., Shepherd, T. G. & Vallis, G. K. 1995 Rossby number expansions, slaving principles and balance dynamics. Q. J. R. Meteorol. Soc. 121, 723–739.CrossRefGoogle Scholar
Young, W. R. 1986 Elliptical vortices in shallow water. J. Fluid Mech. 171, 101–119.CrossRefGoogle Scholar
Zhmur, V. V. & Shchepetkin, A. F. 1991 Evolution of an ellipsoidal vortex in a stratified ocean: survivability of the vortex in flow with vertical shear. Izv. Akad. Nauk SSSR Atmos. Ocean. Phys. 27, 492–503.Google Scholar
Žunić, J., Kopanja, L. & Fieldsend, J. E. 2006 Notes on shape orientation where the standard method does not work. Pattern Recognit. 39, 856–865.CrossRefGoogle Scholar

Tsang and Dritschel supplementary movie

A quasi-stable vortex remains close to its initial shape during the whole simulation of several hundreds inertial periods.

Download Tsang and Dritschel supplementary movie(Video)
Video 4.4 MB

Tsang and Dritschel supplementary movie

A strongly horizontally elongated vortex develops a dumbbell shape before breaking up into a binary system.

Download Tsang and Dritschel supplementary movie(Video)
Video 15.4 MB

Tsang and Dritschel supplementary movie

An unstable vortex becomes tilted as it evolves from its initial ellipsoidal shape into a columnar shape. The equilibrium shape is almost cylindrical with a tilt angle of about 35 degree.

Download Tsang and Dritschel supplementary movie(Video)
Video 16.1 MB

Tsang and Dritschel supplementary movie

An unstable vortex undergoes strong filament shedding. The filaments spun off from the top of the vortex form a long-lived ring which dissipates eventually.

Download Tsang and Dritschel supplementary movie(Video)
Video 4.5 MB

Tsang and Dritschel supplementary movie

This vortex starts to tumble as it becomes unstable. It then deforms and spins off filaments as it approaches an equilibrium state in which it develops a roughly ellipsoidal shape and continues to tumble.

Download Tsang and Dritschel supplementary movie(Video)
Video 5.6 MB

Tsang and Dritschel supplementary movie

After an initial period of steady rotation, this vortex starts to tumble while maintaining its original ellipsoidal shape.

Download Tsang and Dritschel supplementary movie(Video)
Video 3.6 MB

Tsang and Dritschel supplementary movie

A vortex oscillates between its initial ellipsoidal shape and a non-ellipsoidal shape. The top and bottom ends of the vortex are moving in phase.

Download Tsang and Dritschel supplementary movie(Video)
Video 2.9 MB

Tsang and Dritschel supplementary movie

After initial strong filament shedding, this vortex settles down in an oscillation between an upright and a slanted columnar shape, an example of shape oscillation in which the top and bottom ends of the vortex move out of phase.

Download Tsang and Dritschel supplementary movie(Video)
Video 3.9 MB