Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-25T21:08:15.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Doubly symmetric finite-core heton equilibria

Published online by Cambridge University Press:  15 August 2012

V. G. Makarov ,
M. A. Sokolovskiy  and
Z. Kizner
V. G. Makarov
Affiliation:
Interdisciplinary Center of Marine Sciences of the National Polytechnic Institute, La Paz, Baja California Sur 23096, Mexico
M. A. Sokolovskiy
Affiliation:
Water Problems Institute of the Russian Academy of Sciences, 3 Gubkina Str. 119333, Moscow, Russia
Z. Kizner*
Affiliation:
Departments of Physics and Mathematics, Bar-Ilan University, Ramat-Gan 52900, Israel
*
†Email address for correspondence: Ziv.Kizner@biu.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

A finite-core heton is a baroclinic 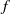-plane modon of a special type: it is composed of two patches of uniform quasi-geostrophic potential vorticity (PV) residing in different layers of a two-layer rotating fluid. This paper focuses on numerical construction of steadily translating, doubly symmetric, finite-core hetons and testing their stability. Such a heton, which possesses symmetry about the translation axis and the transverse axis, is a stationary solution to the equations of PV conservation in each of the layers when considered in a comoving frame of reference. When constructing the heton solutions and examining their bifurcations, we identify a heton by a pair of independent non-dimensional parameters, the half-length (in the translation direction) of a PV patch and the distance of the front point of the upper patch from the translation axis. The advantage of this method over other tried approaches is that it allows one to obtain solutions of new, previously unknown types. The results of testing the heton stability are presented on the plane made by a mean radius of a PV patch and the (horizontal) separation between the centroids of the patches. Two kinds of stability are tested separately, the stability to arbitrary perturbations that do not preserve the symmetry of the initial state and the stability to so-called symmetric perturbations that do not violate the initial symmetry. The hetons comparable in size with the Rossby radius, and smaller, are always stable in both senses. However, when some critical size is exceeded, the heton stability becomes dependent on the separation, and the larger the heton, the higher the separation required for stability. The separation guaranteeing the stability to symmetric perturbations is smaller than that required for the stability to arbitrary perturbations. Interrelations between instabilities and bifurcations are briefly discussed.

JFM classification

Vortex Flows: Contour dynamics Geophysical and Geological Flows: Rotating flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 708 , 10 October 2012 , pp. 397 - 417
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Chaplygin, S. A. 1903 One case of vortex motion in fluid. Trans. Phys. Sect. Imperial Moscow Soc. Friends Nat. Sci. 11 (2), 11–14 (English translation: Chaplygin, S. A. 2007 One case of vortex motion in fluid. Regul. Chaotic. Dyn. 12 (2), 102–114).Google Scholar
2. Deem, G. S. & Zabusky, N. J. 1978 Vortex waves: stationary ‘V-states’, interactions, recurrence, and breaking. Phys. Rev. Lett. 40, 859–862.CrossRefGoogle Scholar
3. Dritschel, D. G. 1988 Contour surgery – a topological reconnection scheme for extended integrations using contour dynamics. J. Comput. Phys. 77, 240–266.CrossRefGoogle Scholar
4. Dritschel, D. G. 1989 Contour dynamics and contour surgery: numerical algorithms for extended, high-resolution modelling of vortex dynamics in two-dimensional, inviscid, incompressible flows. Comput. Phys. Rep. 10, 77–146.CrossRefGoogle Scholar
5. Dritschel, D. G. 1995 A general theory for two-dimensional vortex interactions. J. Fluid Mech. 293, 269–303.CrossRefGoogle Scholar
6. Flierl, G. R. 1988 On the stability of geostrophic vortices. J. Fluid Mech. 197, 349–388.CrossRefGoogle Scholar
7. Flierl, G. R., Larichev, V. D., McWilliams, J. & Reznik, G. M. 1980 The dynamics of baroclinic and barotropic solitary eddies. Dyn. Atmos. Oceans 5, 1–41.CrossRefGoogle Scholar
8. Gryanik, G. R. 1983 Dynamics of singular geostrophic vortices in a two-layer model of the atmosphere (ocean). Izv. Atmos. Ocean Phys. 19, 227–240.Google Scholar
9. Helfrich, K. R. & Send, U. 1988 Finite-amplitude evolution of two-layer geostrophic vortices. J. Fluid Mech. 197, 331–348.CrossRefGoogle Scholar
10. Hesthaven, J. S., Lynov, J. P. & Nycander, J. 1993 Dynamics of nonstationary dipole vortices. Phys. Fluids A 5, 622–629.CrossRefGoogle Scholar
11. Hogg, N. G. & Stommel, H. M. 1985 The heton, an elementary interaction between discrete baroclinic geostrophic vortices, and its implications concerning eddy heat-flow. Proc. R. Soc. Lond. A 397, 1–20.Google Scholar
12. Khvoles, R., McWilliams, J. C. & Kizner, Z. 2007 Non-coincidence of separatrices in two-layer modons. Phys. Fluids 19, 056602.Google Scholar
13. Kizner, Z. I. 1984 Rossby solitons with axisymmetrical baroclinic modes. Dokl. USSR Acad. Sci. 275, 1495–1498.Google Scholar
14. Kizner, Z. I. 1997 Solitary Rossby waves with baroclinic modes. J. Mar. Res. 55, 671–685.CrossRefGoogle Scholar
15. Kizner, Z. 2006 Stability and transitions of hetonic quartets and baroclinic modons. Phys. Fluids 18 (5), 056601.CrossRefGoogle Scholar
16. Kizner, Z. 2008 Hetonic quartet: exploring the transitions in baroclinic modons. In IUTAM Symposium on Hamiltonian Dynamics, Vortex Structures, Turbulence, IUTAM Bookseries (ed. Borisov, A. V. et al. ), vol. 6, pp. 125–133. Springer.CrossRefGoogle Scholar
17. Kizner, Z. 2011 Stability of point-vortex multipoles revisited. Phys. Fluids 23, 064104.CrossRefGoogle Scholar
18. Kizner, Z., Berson, D. & Khvoles, R. 2002 Baroclinic modon equilibria on the beta-plane: stability and transitions. J. Fluid Mech. 468, 239–270.CrossRefGoogle Scholar
19. Kizner, Z., Berson, D & Khvoles, R. 2003a Non-circular baroclinic modons: constructing stationary solutions. J. Fluid Mech. 489, 199–228.CrossRefGoogle Scholar
20. Kizner, Z., Berson, D., Reznik, G. & Sutyrin, G. 2003b The theory of the beta-plane baroclinic topographic modons. Geophys. Astrophys. Fluid Dyn. 97, 175–211.CrossRefGoogle Scholar
21. Kozlov, V. F., Makarov, V. G. & Sokolovskiy, M. A. 1986 Numerical model of the baroclinic instability of axially symmetric eddies in two-layer ocean. Izv. Atmos. Ocean. Phys. 22, 674–678.Google Scholar
22. Lamb, H. 1895 Hydrodynamics, 2nd edn. Cambridge, Cambridge University Press.CrossRefGoogle Scholar
23. Larichev, V. D. & Reznik, G. M. 1976 Two-dimensional solitary Rossby waves. Dokl. Acad. Nauk USSR 231, 1077–1080.Google Scholar
24. Makarov, V. G. 1991 Computational algorithm of the contour dynamics method with changeable topology of domains under study. Model. Mekh. 5, 83–95.Google Scholar
25. Makarov, V. G & Kizner, Z. 2011 Stability and evolution of uniform-vorticity dipoles. J. Fluid Mech. 672, 307–325.CrossRefGoogle Scholar
26. Pierrehumbert, R. T. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99, 129–144.CrossRefGoogle Scholar
27. Polvani, L. M. 1991 Two-layer geostrophic vortex dynamics. Part 2. Alignment and two-layer V-states. J. Fluid Mech. 225, 241–270.CrossRefGoogle Scholar
28. Polvani, L. M., Zabusky, N. J. & Flierl, G. R. 1988 Applications of contour dynamics to two-layer quasi-geostrophic flows. Fluid Dyn. Res. 3, 422–424.CrossRefGoogle Scholar
29. Reznik, G. M. & Sutyrin, G. G. 2001 Baroclinic topographic modons. J. Fluid Mech. 431, 121–142.CrossRefGoogle Scholar
30. Sadovskii, V. S. 1971 Vortex regions in a potential stream with a jump of Bernoulli’s constant at the boundary. Z. Angew. Math. Phys.: J. Appl. Maths Mech. 35, 773–779.Google Scholar
31. Sokolovskiy, M. A. 1988 Numerical modelling of nonlinear instability for axisymmetric two-layer vortices. Izv. Atmos. Ocean. Phys. 24, 536–542.Google Scholar
32. Sokolovskiy, M. A. & Verron, J. 2000 Finite-core hetons: stability and interactions. J. Fluid Mech. 423, 127–154.CrossRefGoogle Scholar
33. Wu, H. M., Overman, II, E. A. & Zabusky, N. J. 1984 Steady-state solutions of the Euler equations: rotating and translating V-states with limiting cases. I. Numerical algorithms and results. J. Comput. Phys. 53, 42–71.CrossRefGoogle Scholar
34. Zabusky, N. J., Hughes, M. N. & Roberts, K. V. 1979 Contour dynamics for the Euler equations in two-dimensions. J. Comput. Phys. 30, 96–106.CrossRefGoogle Scholar