Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-23T23:33:24.701Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of oblique breakdown in a supersonic boundary layer employing a local cooling strip

Published online by Cambridge University Press:  23 September 2022

Teng Zhou Open the ORCID record for Teng Zhou [Opens in a new window] ,
Zaijie Liu Open the ORCID record for Zaijie Liu [Opens in a new window] ,
Yuhan Lu Open the ORCID record for Yuhan Lu [Opens in a new window] ,
Dake Kang  and
Chao Yan Open the ORCID record for Chao Yan [Opens in a new window]
Teng Zhou
Affiliation:
National Key Laboratory of Computational Fluid Dynamics, Beihang University, Beijing 100191, PR China
Zaijie Liu
Affiliation:
National Key Laboratory of Computational Fluid Dynamics, Beihang University, Beijing 100191, PR China
Yuhan Lu
Affiliation:
National Key Laboratory of Computational Fluid Dynamics, Beihang University, Beijing 100191, PR China
Dake Kang
Affiliation:
National Key Laboratory of Computational Fluid Dynamics, Beihang University, Beijing 100191, PR China
Chao Yan*
Affiliation:
National Key Laboratory of Computational Fluid Dynamics, Beihang University, Beijing 100191, PR China
*
†Email address for correspondence: yanchao@buaa.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

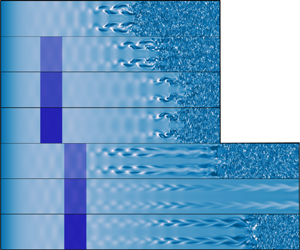
Oblique breakdown in a Mach 2.0 supersonic boundary layer controlled by a local cooling strip with a temperature jump is investigated using direct numerical simulations and linear stability theory. The effect of temperature on the stability of the fundamental oblique waves is first studied by linear stability theory. It is shown that the growth rate of fundamental oblique waves will decrease monotonically as the temperature decreases. However, the results of the direct numerical simulations indicate that transition reversal will occur as the growth rate of the fundamental oblique waves of cooled case becomes faster compared with that of baseline case downstream of the cooling strip. When the cooling strip is in the linear region, the transition is delayed due to the suppression effect of the cooling strip on the fundamental oblique waves. When the cooling strip is located in the early nonlinear region, the fundamental oblique waves will be suppressed by higher spanwise wavenumber steady modes generated by the mutual and self-interaction between the fundamental oblique waves and harmonic modes, which is first called the self-suppression effect (SSE) in the present study. Further research indicated that the meanflow distortion generated by steady modes plays an important role in the SSE. Compared with the stabilization effect of the cooling strip, the SSE is more effective. Moreover, the SSE might provide a new idea on the instability control, as it is observed that the SSE works three times leading to the growth rate of fundamental oblique waves slowing down at three different regions, respectively.

JFM classification

Compressible Flows: Supersonic flow Flow Control: Instability control Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 949 , 25 October 2022 , A4
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagheri, S. & Hanifi, A. 2007 The stabilizing effect of streaks on Tollmien–Schlichting and oblique waves: a parametric study. Phys. Fluids 19 (7), 078103.CrossRefGoogle Scholar
Bradshaw, P. 1977 Efficient implementation of weighted ENO schemes. Annu. Rev. Fluid Mech. 9, 33–54.CrossRefGoogle Scholar
Chang, C.-L. & Malik, M.R. 1994 Oblique-mode breakdown and secondary instability in supersonic boundary layers. J. Fluid Mech. 273, 323–360.CrossRefGoogle Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1 (2), 191–226.CrossRefGoogle Scholar
Corke, T.C. & Mangano, R.A. 1989 Resonant growth of three-dimensional modes in trnsitioning Blasius boundary layers. J. Fluid Mech. 209, 93–150.CrossRefGoogle Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14 (8), L57–L60.CrossRefGoogle Scholar
Fasel, H, Thumm, A. & Bestek, H. 1993 Direct numerical simulation of transition in supersonic boundary layers: oblique breakdown. In Fluids Engineering Conference, pp. 77–92. ASME.Google Scholar
Fedorov, A.V. & Khokhlov, A.P. 2002 Receptivity of hypersonic boundary layer to wall disturbances. Theor. Comput. Fluid Dyn. 15 (4), 231–254.CrossRefGoogle Scholar
Fedorov, A., Soudakov, V., Egorov, I., Sidorenko, A., Gromyko, Y., Bountin, D., Polivanov, P. & Maslov, A. 2015 High-speed boundary-layer stability on a cone with localized wall heating or cooling. AIAA J. 53 (9), 2512–2524.CrossRefGoogle Scholar
Fezer, A. & Kloker, M.J. 2000 Spatial direct numerical simulation of transition phenomena in supersonic flat-plate boundary layers. In Laminar-Turbulent Transition, pp. 415–420. Springer.CrossRefGoogle Scholar
Franko, K.J. & Lele, S.K. 2013 Breakdown mechanisms and heat transfer overshoot in hypersonic zero pressure gradient boundary layers. J. Fluid Mech. 730, 491–532.CrossRefGoogle Scholar
Franko, K.J. & Lele, S. 2014 Effect of adverse pressure gradient on high speed boundary layer transition. Phys. Fluids 26 (2), 024106.CrossRefGoogle Scholar
Fransson, J.H.M., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17 (5), 054110.Google Scholar
Fransson, J.H.M., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96 (6), 064501.CrossRefGoogle ScholarPubMed
Holloway, P.F. & Sterrett, J.R. 1964 Effect of controlled surface roughness on boundary-layer transition and heat transfer at Mach number of 4.8 and 6.0. NASA Tech. Note D-2054.CrossRefGoogle Scholar
Inger, G.R. & Gnoffo, P.A. 2001 Analytical and computational study of wall temperature jumps in supersonic flow. AIAA J. 39 (1), 79–87.Google Scholar
Jahanbakhshi, R. & Zaki, T.A. 2021 Optimal heat flux for delaying transition to turbulence in a high-speed boundary layer. J. Fluid Mech. 916, A46.CrossRefGoogle Scholar
Jiang, G.S. & Shu, C.W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.Google Scholar
Jiang, L., Choudhari, M., Chang, C.-L. & Liu, C.-Q. 2006 Numerical simulations of laminar-turbulent transition in supersonic boundary layer. In 36th AIAA Fluid Dynamics Conference and Exhibit, pp. 32–24.Google Scholar
Kneer, S. 2020 Control of laminar breakdown in a supersonic boundary layer employing streaks. Master's thesis, University of Stuttgart.CrossRefGoogle Scholar
Kneer, S., Guo, Z.-F. & Kloker, M.J. 2022 Control of laminar breakdown in a supersonic boundary layer employing streaks. J. Fluid Mech. 932, A53.CrossRefGoogle Scholar
Kosinov, A.D., Maslov, A.A. & Semionov, N.V. 1997 An experimental study of generation of unstable disturbances on the leading edge of a plate at $M=2$. J. Appl. Mech. Tech. Phys. 38 (1), 45–51.CrossRefGoogle Scholar
Kosinov, A.D., Semionov, N.V. & Shevelkov, S.G. 1994 Investigation of supersonic boundary layer stability and transition using controlled disturbances. In 7th International Conference on the Methods of Aerophisical Research.Google Scholar
Kurz, H.B.E. & Kloker, M.J. 2016 Mechanisms of flow tripping by discrete roughness elements in a swept-wing boundary layer. J. Fluid Mech. 796, 158–194.CrossRefGoogle Scholar
Laible, A.C. & Fasel, H.F. 2016 Continuously forced transient growth in oblique breakdown for supersonic boundary layers. J. Fluid Mech. 804, 323–350.CrossRefGoogle Scholar
Lees, L. & Lin, C.C. 1946 Investigation of the Stability of the Laminar Boundary Layer in a Compressible Fluid. NACA.Google Scholar
Leib, S.J. & Lee, S.S. 1995 Nonlinear evolution of a pair of oblique instability waves in a supersonic boundary layer. J. Fluid Mech. 282, 339–371.CrossRefGoogle Scholar
Li, X., Tong, F.-L., Yu, C.-P. & Li, X.-L. 2019 Statistical analysis of temperature distribution on vortex surfaces in hypersonic turbulent boundary layer. Phys. Fluids 31 (10), 106101.Google Scholar
Li, X.-L., Fu, D.-X. & Ma, Y. 2010 a Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack. Phys. Fluids 22 (2), 025105.CrossRefGoogle Scholar
Li, X.-L., Fu, D.-X., Ma, Y.-W. & Liang, X. 2010 b Development of high accuracy CFD software hoam-OpenCFD. e-Sci. Technol. Appl. 1, 53–59.Google Scholar
Li, X.-L., Leng, Y. & He, Z.-W. 2013 Optimized sixth-order monotonicity-preserving scheme by nonlinear spectral analysis. Intl J. Numer. Meth. Fluids 73 (6), 560–577.CrossRefGoogle Scholar
Lysenko, V.I. & Maslov, A.A. 1984 The effect of cooling on supersonic boundary-layer stability. J. Fluid Mech. 147, 39–52.Google Scholar
Ma, Y.-B. & Zhong, X.-L. 2003 Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions. J. Fluid Mech. 488, 31–78.CrossRefGoogle Scholar
Mack, L.M. 1984 Boundary-layer linear stability theory. Tech. Rep. California Institute of Technology, Jet Propulsion Laboratory.Google Scholar
Malik, M.R. 1989 Prediction and control of transition in supersonic and hypersonic boundary layers. AIAA J. 27 (11), 1487–1493.Google Scholar
Masad, J.A. & Abid, R. 1995 On transition in supersonic and hypersonic boundary layers. Intl J. Engng Sci. 33 (13), 1893–1919.CrossRefGoogle Scholar
Mayer, C.S.J., Fasel, H.F., Choudhari, M. & Chang, C.-L. 2014 Transition onset predictions for oblique breakdown in a Mach 3 boundary layer. AIAA J. 52 (4), 882–885.CrossRefGoogle Scholar
Mayer, C.S.J., Wernz, S. & Fasel, H.F. 2011 a Numerical investigation of the nonlinear transition regime in a Mach 2 boundary layer. J. Fluid Mech. 668, 113–149.CrossRefGoogle Scholar
Mayer, C.S.J., Von Terzi, D.A. & Fasel, H.F. 2011 b Direct numerical simulation of complete transition to turbulence via oblique breakdown at Mach 3. J. Fluid Mech. 674, 5–42.Google Scholar
Morkovin, M.V. 1983 Understanding transition to turbulence in shear layers. Tech. Rep. Illinois Inst of Tech Chicago Dept of Mechanics Mechanical and Aerospace.Google Scholar
Oz, F. & Kara, K. 2021 Effects of local cooling on hypersonic boundary-layer stability. AIAA Scitech 2021 Forum. AIAA Paper 2021-0940.CrossRefGoogle Scholar
Paredes, P., Choudhari, M.M. & Li, F. 2017 Instability wave–streak interactions in a supersonic boundary layer. J. Fluid Mech. 831, 524–553.CrossRefGoogle Scholar
Shahinfar, S., Sattarzadeh, S.S., Fransson, J.H.M. & Talamelli, A. 2012 Revival of classical vortex generators now for transition delay. Phys. Rev. Lett. 109 (7), 074501.CrossRefGoogle ScholarPubMed
Sharma, S., Shadloo, M.S. & Hadjadj, A. 2019 a Effect of thermo-mechanical non-equilibrium on the onset of transition in supersonic boundary layer. Heat Mass Transf. 55, 1849–1861.CrossRefGoogle Scholar
Sharma, S., Shadloo, M.S., Hadjadj, A. & Kloker, M.J. 2019 b Control of oblique-type breakdown in a supersonic boundary layer employing streaks. J. Fluid Mech. 873, 1072–1089.CrossRefGoogle Scholar
Soudakov, V.G., Egorov, I.V. & Fedorov, A.V. 2009 Numerical simulation of receptivity of a hypersonic boundary layer over a surface with temperature jump. In 6th European Symposium on Aerothermodynamics for Space Vehicles, p. 66.Google Scholar
Steger, J.L. & Warming, R.F. 1981 Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods. J. Comput. Phys. 40 (2), 263–293.CrossRefGoogle Scholar
Stetson, K. & Kimmel, R. 1992 On hypersonic boundary-layer stability. In 30th Aerospace Sciences Meeting and Exhibit, AIAA Paper 92-0737.Google Scholar
Stewartson, K. 1964 The Theory of Laminar Boundary Layers in Compressible Fluids. Oxford University Press.CrossRefGoogle Scholar
Tumin, A. 2007 Three-dimensional spatial normal modes in compressible boundary layers. J. Fluid Mech. 586, 295–322.CrossRefGoogle Scholar
Van Driest, E.R. 1951 Turbulent boundary layer in compressible fluids. J. Aeronaut. Sci. 18 (3), 145–160.CrossRefGoogle Scholar
White, F.M. 2006 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Zhao, R., Wen, C.-Y., Tian, X.-D., Long, T.-H. & Yuan, W. 2018 Numerical simulation of local wall heating and cooling effect on the stability of a hypersonic boundary layer. Intl J. Heat Mass Transfer 121, 986.CrossRefGoogle Scholar
Zhou, T., Lu, Y.-H., Liu, Z.-J. & Yan, C. 2021 Direct numerical simulation of control of oblique breakdown in a supersonic boundary layer using a local cooling strip. Phys. Fluids 33 (8), 084101.CrossRefGoogle Scholar