Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-24T02:27:10.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Complex singularities near the intersection of a free surface and wall. Part 1. Vertical jets and rising bubbles

Published online by Cambridge University Press:  04 October 2018

Thomas G. J. Chandler  and
Philippe H. Trinh Open the ORCID record for Philippe H. Trinh [Opens in a new window]
Thomas G. J. Chandler
Affiliation:
Oxford Centre for Industrial and Applied Mathematics, Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK
Philippe H. Trinh*
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK
*
†Email address for correspondence: p.trinh@bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that in steady-state potential flows, the separation of a gravity-driven free surface from a solid exhibits a number of peculiar characteristics. For example, it can be shown that the fluid must separate from the body so as to form one of three possible in-fluid angles: (i) 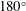$180^{\circ }$, (ii) 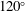$120^{\circ }$ or (iii) an angle such that the surface is locally perpendicular to the direction of gravity. These necessary separation conditions were notably remarked upon by Dagan & Tulin (J. Fluid Mech., vol. 51 (3), 1972, pp. 529–543) in the context of ship hydrodynamics, but they are of crucial importance in many potential-flow applications. It is not particularly well understood why there is such a drastic change in the local separation behaviours when the global flow is altered. The question that motivates this work is the following: outside of a formal balance-of-terms argument, why must cases (i)–(iii) occur and furthermore, what are the connections between them? In this work, we seek to explain the transitions between the three cases in terms of the singularity structure of the associated solutions once they are extended into the complex plane. A numerical scheme is presented for the analytic continuation of a vertical jet (or alternatively a rising bubble). It will be shown that the transition between the three cases can be predicted by observing the coalescence of singularities as the speed of the jet is modified. A scaling law is derived for the coalescence rate of singularities.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 323 - 350
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, G. R. 1990 Singularities in the complex physical plane. In Hyperbolic Problems (ed. Engquist, B. & Gustafson, B.). Studentlitteratur.Google Scholar
Baker, G. R. & Xie, C. 2011 Singularities in the complex physical plane for deep water waves. J. Fluid Mech. 685, 83–116.Google Scholar
Birkhoff, G. & Carter, D. 1957 Rising plane bubbles. J. Ration. Mech. Anal. 6, 769–779.Google Scholar
Chandler, T. G. J. & Trinh, P. H.2018 Complex singularities near the intersection of a free surface and wall. Part 2. Angled nozzles. (In preparation.)Google Scholar
Chapman, S. J. 1999 On the role of Stokes lines in the selection of Saffman–Taylor fingers with small surface tension. Eur. J. Appl. Maths 10 (6), 513–534.Google Scholar
Combescot, R., Hakim, V., Dombre, T., Pomeau, Y. & Pumir, A. 1986 Shape selection of Saffman–Taylor fingers. Phys. Rev. A 56 (19), 2036–2039.Google Scholar
Couët, B. & Strumolo, G. S. 1987 The effects of surface tension and tube inclination on a two-dimensional rising bubble. J. Fluid Mech. 184, 1–14.Google Scholar
Cowley, S. J., Baker, G. R. & Tanveer, S. 1999 On the formation of moore curvature singularities in vortex sheets. J. Fluid Mech. 378, 233–267.Google Scholar
Crew, S. C. & Trinh, P. H. 2016 New singularities for Stokes waves. J. Fluid Mech. 798, 256–283.Google Scholar
Dagan, G. & Tulin, M. P. 1972 Two-dimensional free-surface gravity flow past blunt bodies. J. Fluid Mech. 51 (3), 529–543.Google Scholar
Daripa, P. 2000 A computational study of rising plane Taylor bubbles. J. Comput. Phys. 157 (1), 120–142.Google Scholar
Farrow, D. E. & Tuck, E. O. 1995 Further studies of stern wavemaking. J. Austral. Math. Soc. B 36, 424–437.Google Scholar
Garabedian, P. R. 1957 On steady-state bubbles generated by Taylor instability. Proc. R. Soc. Lond. A 241, 423–431.Google Scholar
Garabedian, P. R. 1985 A remark about pointed bubbles. Commun. Pure Appl. Maths 38 (5), 609–612.Google Scholar
Goh, K. H. M.1986 Numerical solution of quadratically non-linear boundary value problems using integral equation techniques with application to nozzle and wall flows. PhD thesis, University of Adelaide.Google Scholar
Goh, K. H. M. & Tuck, E. O. 1985 Thick waterfalls from horizontal slots. J. Engng Maths 19 (4), 341–349.Google Scholar
Golubeva, N.2003 Singularities in the spatial complex plane for vortex sheets and thin vortex layers. PhD thesis, The Ohio State University.Google Scholar
Grant, M. A. 1973 The singularity at the crest of a finite amplitude progressive Stokes wave. J. Fluid Mech. 59, 257–262.Google Scholar
Lee, J. & Vanden-Broeck, J.-M. 1993 Two-dimensional jets falling from funnels and nozzles. Phys. Fluids 5 (10), 2454–2460.Google Scholar
Longuet-Higgins, M. S. & Fox, M. J. H. 1978 Theory of the almost-highest wave. Part 2. Matching and analytic extension. J. Fluid Mech. 85, 769–786.Google Scholar
McCue, S. W. & Forbes, L. K. 1999 Bow and stern flows with constant vorticity. J. Fluid Mech. 399, 277–300.Google Scholar
McCue, S. W. & Forbes, L. K. 2002 Free-surface flows emerging from beneath a semi-infinite plate with constant vorticity. J. Fluid Mech. 461, 387–407.Google Scholar
Meiron, D. I., Baker, G. R. & Orszag, S. A. 1982 Analytic structure of vortex sheet dynamics. Part 1. Kelvin–Helmholtz instability. J. Fluid Mech. 114, 283–298.Google Scholar
Milewski, P., Vanden-Broeck, J.-M. & Keller, J. B. 1998 Singularities on free surfaces of fluid flows. Stud. Appl. Maths 100 (3), 245–267.Google Scholar
Moore, D. W. 1979 The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc. R. Soc. Lond. A 365 (1720), 105–119.Google Scholar
Norman, A. C. 1974 Expansions for the shape of maximum amplitude stokes waves. J. Fluid Mech. 66 (02), 261–265.Google Scholar
Tanveer, S. 1991 Singularities in water waves and Rayleigh–Taylor instablity. Proc. R. Soc. Lond. A 435, 137–158.Google Scholar
Trinh, P. H. 2016 A topological study of gravity waves generated by moving bodies using the method of steepest descents. Proc. R. Soc. Lond A 472, 20150833.Google Scholar
Trinh, P. H. & Chapman, S. J. 2014 The wake of a two-dimensional ship in the low-speed limit: results for multi-cornered hulls. J. Fluid Mech. 741, 492–513.Google Scholar
Trinh, P. H., Chapman, S. J. & Vanden-Broeck, J.-M. 2011 Do waveless ships exist? Results for single-cornered hulls. J. Fluid Mech. 685, 413–439.Google Scholar
Tuck, E. O. 1987 Efflux from a slit in a vertical wall. J. Fluid Mech. 176, 253–264.Google Scholar
Tuck, E. O. & Roberts, A. J. 1997 Bow-like free surfaces under gravity. Phil. Trans. R. Soc. Lond. A 355, 655–677.Google Scholar
Vanden-Broeck, J.-M. 1984a Bubbles rising in a tube and jets falling from a nozzle. Phys. Fluids 27 (5), 1090–1093.Google Scholar
Vanden-Broeck, J.-M. 1984b Rising bubbles in a two-dimensional tube with surface tension. Phys. Fluids 27 (11), 2604–2607.Google Scholar
Vanden-Broeck, J.-M. 1991 Axisymmetric jet falling from a vertical nozzle and bubble rising in a tube of circular cross section. Phys. Fluids A 3 (2), 258–262.Google Scholar
Vanden-Broeck, J.-M. 2010 Gravity-Capillary Free-Surface Flows. Cambridge University Press.Google Scholar
Vanden-Broeck, J.-M. & Tuck, E. O. 1994 Flow near the intersection of a free surface with a vertical wall. SIAM J. Appl. Maths 54 (1), 1–13.Google Scholar