Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-19T19:53:24.127Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison of variational balance models for the rotating shallow water equations

Published online by Cambridge University Press:  07 June 2017

David G. Dritschel ,
Georg A. Gottwald Open the ORCID record for Georg A. Gottwald [Opens in a new window]  and
Marcel Oliver
David G. Dritschel*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
Georg A. Gottwald*
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia
Marcel Oliver*
Affiliation:
School of Engineering and Science, Jacobs University, 28759 Bremen, Germany
*
†Email addresses for correspondence: david.dritschel@st-andrews.ac.uk, georg.gottwald@sydney.edu.au, oliver@member.ams.org
†Email addresses for correspondence: david.dritschel@st-andrews.ac.uk, georg.gottwald@sydney.edu.au, oliver@member.ams.org
†Email addresses for correspondence: david.dritschel@st-andrews.ac.uk, georg.gottwald@sydney.edu.au, oliver@member.ams.org
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an extensive numerical comparison of a family of balance models appropriate to the semi-geostrophic limit of the rotating shallow water equations, and derived by variational asymptotics in Oliver (J. Fluid Mech., vol. 551, 2006, pp. 197–234) for small Rossby numbers 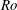$Ro$. This family of generalized large-scale semi-geostrophic (GLSG) models contains the 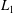$L_{1}$-model introduced by Salmon (J. Fluid Mech., vol. 132, 1983, pp. 431–444) as a special case. We use these models to produce balanced initial states for the full shallow water equations. We then numerically investigate how well these models capture the dynamics of an initially balanced shallow water flow. It is shown that, whereas the 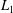$L_{1}$-member of the GLSG family is able to reproduce the balanced dynamics of the full shallow water equations on time scales of 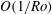$O(1/Ro)$ very well, all other members develop significant unphysical high wavenumber contributions in the ageostrophic vorticity which spoil the dynamics.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Shallow water flows Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 689 - 716
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, J. S. & Holm, D. D. 1996 Extended-geostrophic Hamiltonian models for rotating shallow water motion. Phys. D 98 (2), 229–248.Google Scholar
Allen, J. S., Holm, D. D. & Newberger, P. A. 2002 Toward an extended-geostrophic Euler–Poincaré model for mesoscale oceanographic flow. In Large-scale Atmosphere–ocean Dynamics (ed. Norbury, J. & Roulstone, I.), vol. 1, pp. 101–125. Cambridge University Press.Google Scholar
Benamou, J. D. & Brenier, Y. 1998 Weak existence for the semigeostrophic equations formulated as a coupled Monge–Ampère/transport problem. SIAM J. Appl. Maths 58 (5), 1450–1461.Google Scholar
Bloom, S. C., Takacs, L. L., Da Silva, A. M. & Ledvina, D. 1996 Data assimilation using incremental analysis updates. Mon. Weath. Rev. 124, 1256–1271.2.0.CO;2>CrossRefGoogle Scholar
Bretherton, F. P. 1970 A note on Hamilton’s principle for perfect fluids. J. Fluid Mech. 44, 19–31.Google Scholar
Çalık, M. & Oliver, M. 2013 Weak solutions for generalized large-scale semigeostrophic equations. Commun. Pure Appl. Anal. 12 (2), 939–953.Google Scholar
Çalık, M., Oliver, M. & Vasylkevych, S. 2013 Global well-posedness for the generalized large-scale semigeostrophic equations. Arch. Rat. Mech. Anal. 207 (3), 969–990.Google Scholar
Cullen, M. J. P. 2008 A comparison of numerical solutions to the eady frontogenesis problem. Q. J. R. Meteorol. Soc. 134 (637), 2143–2155.Google Scholar
Cullen, M. J. P. & Purser, R. J. 1984 An extended Lagrangian theory of semi-geostrophic frontogenesis. J. Atmos. Sci. 41 (9), 1477–1497.2.0.CO;2>CrossRefGoogle Scholar
Eliassen, A. 1948 The quasi-static equations of motion with pressure as independent variable. Geophys. Publ. 17, 1–44.Google Scholar
Goldstein, H. 1980 Classical Mechanics, 2nd edn. Addison-Wesley.Google Scholar
Gottwald, G. A. 2014 Controlling balance in an ensemble Kalman filter. Nonlinear Process. Geophys. 21, 417–426.Google Scholar
Gottwald, G. A. & Oliver, M. 2014 Slow dynamics via degenerate variational asymptotics. Proc. R. Soc. Lond. A 470 (2170), 20140460.Google Scholar
Greybush, S. J., Kalnay, E., Miyoshi, T., Ide, K. & Hunt, B. R. 2011 Balance and ensemble Kalman filter localization techniques. Mon. Weath. Rev. 139 (2), 511–522.CrossRefGoogle Scholar
Hoskins, B. J. 1975 The geostrophic momentum approximation and the semi-geostrophic equations. J. Atmos. Sci. 32 (2), 233–242.Google Scholar
Kepert, J. D. 2009 Covariance localisation and balance in an ensemble Kalman filter. Q. J. R. Meteorol. Soc. 135 (642), 1157–1176.Google Scholar
Lynch, P. 2006 The Emergence of Numerical Weather Prediction: Richardson’s Dream. Cambridge University Press.Google Scholar
McIntyre, M. E. & Roulstone, I. 2002 Are there higher-accuracy analogues of semigeostrophic theory? In Large-scale Atmosphere–ocean Dynamics (ed. Norbury, J. & Roulstone, I.), vol. 2, pp. 301–364. Cambridge University Press.Google Scholar
Mitchell, H. L., Houtekamer, P. L. & Pellerin, G. 2002 Ensemble size, balance, and model-error representation in an ensemble Kalman filter. Mon. Weath. Rev. 130 (11), 2791–2808.Google Scholar
Mohebalhojeh, A. R. & Dritschel, D. G. 2001 Hierarchies of balance conditions for the f-plane shallow-water equations. J. Atmos. Sci. 58 (16), 2411–2426.Google Scholar
Mohebalhojeh, A. R. & Dritschel, D. G. 2004 Contour-advective semi-Lagrangian algorithms for many-layer primitive equation models. Q. J. R. Meteorol. Soc. 130, 347–364.CrossRefGoogle Scholar
Oliver, M. 2006 Variational asymptotics for rotating shallow water near geostrophy: a transformational approach. J. Fluid Mech. 551, 197–234.CrossRefGoogle Scholar
Oliver, M. & Vasylkevych, S. 2011 Hamiltonian formalism for models of rotating shallow water in semigeostrophic scaling. J. Discrete Continuous Dyn. Syst. 31 (3), 827–846.Google Scholar
Oliver, M. & Vasylkevych, S. 2013 Generalized LSG models with spatially varying Coriolis parameter. J. Geophys. Astrophys. Fluid Dyn. 107, 259–276.Google Scholar
Ourmiéres, Y., Brankart, J. M., Berline, L., Brasseur, P. & Verron, J. 2006 Incremental analysis update implementation into a sequential ocean data assimilation system. J. Atmos. Ocean. Technol. 23, 1729–1744.Google Scholar
Richardson, L. F. 1922 Weather Prediction by Numerical Process. Cambridge University Press.Google Scholar
Salmon, R. 1983 Practical use of Hamilton’s principle. J. Fluid Mech. 132, 431–444.Google Scholar
Salmon, R. 1985 New equations for nearly geostrophic flow. J. Fluid Mech. 153, 461–477.Google Scholar
Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
Smith, R. K. & Dritschel, D. G. 2006 Revisiting the Rossby–Haurwitz wave test case with contour advection. J. Comput. Phys. 217 (2), 473–484.Google Scholar
Viúdez, Á. & Dritschel, D. G. 2004 Optimal potential vorticity balance of geophysical flows. J. Fluid Mech. 521, 343–352.Google Scholar