Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shemer, Lev
2019.
On Evolution of Young Wind Waves in Time and Space.
Atmosphere,
Vol. 10,
Issue. 9,
p.
562.
Cao, Tao
Deng, Bing-Qing
and
Shen, Lian
2020.
A simulation-based mechanistic study of turbulent wind blowing over opposing water waves.
Journal of Fluid Mechanics,
Vol. 901,
Issue. ,
Wang, Li-Hao
Zhang, Wu-Yang
Hao, Xuanting
Huang, Wei-Xi
Shen, Lian
Xu, Chun-Xiao
and
Zhang, Zhaoshun
2020.
Surface wave effects on energy transfer in overlying turbulent flow.
Journal of Fluid Mechanics,
Vol. 893,
Issue. ,
Zdyrski, Thomas
and
Feddersen, Falk
2020.
Wind-induced changes to surface gravity wave shape in deep to intermediate water.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Yousefi, Kianoosh
and
Veron, Fabrice
2020.
Boundary layer formulations in orthogonal curvilinear coordinates for flow over wind-generated surface waves.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Yang, Bowen
Jin, Guodong
Wu, Ting
Yang, Zixuan
and
He, Guowei
2020.
Numerical implementation and evaluation of resolvent-based estimation for space–time energy spectra in turbulent channel flows.
Acta Mechanica Sinica,
Vol. 36,
Issue. 4,
p.
775.
Laxague, Nathan J. M.
and
Zappa, Christopher J.
2020.
Observations of mean and wave orbital flows in the ocean’s upper centimetres.
Journal of Fluid Mechanics,
Vol. 887,
Issue. ,
Funke, Christoph S.
Buckley, Marc P.
Schultze, Larissa K.P.
Veron, Fabrice
Timmermans, Mary-Louise E.
and
Carpenter, Jeffrey R.
2021.
Pressure fields in the airflow over wind-generated surface waves.
Journal of Physical Oceanography,
Cao, Tao
and
Shen, Lian
2021.
A numerical and theoretical study of wind over fast-propagating water waves.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Hao, Xuanting
Cao, Tao
and
Shen, Lian
2021.
Mechanistic study of shoaling effect on momentum transfer between turbulent flow and traveling wave using large-eddy simulation.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Zdyrski, Thomas
and
Feddersen, Falk
2021.
Wind-induced changes to surface gravity wave shape in shallow water.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
Mostert, W.
Popinet, S.
and
Deike, L.
2022.
High-resolution direct simulation of deep water breaking waves: transition to turbulence, bubbles and droplets production.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Li, Tianyi
and
Shen, Lian
2022.
The principal stage in wind-wave generation.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
Deskos, Georgios
Ananthan, Shreyas
and
Sprague, Michael A.
2022.
Direct numerical simulations of turbulent flow over misaligned traveling waves.
International Journal of Heat and Fluid Flow,
Vol. 97,
Issue. ,
p.
109029.
Husain, Nyla T.
Hara, Tetsu
and
Sullivan, Peter P.
2022.
Wind Turbulence over Misaligned Surface Waves and Air–Sea Momentum Flux. Part I: Waves Following and Opposing Wind.
Journal of Physical Oceanography,
Vol. 52,
Issue. 1,
p.
119.
Ren, Hehe
and
Laima, Shujin
2022.
Very-large-scale motions in typhoons and one possible original mechanism.
Ocean Engineering,
Vol. 246,
Issue. ,
p.
110568.
Xuan, Anqing
and
Shen, Lian
2022.
Analyses of wave-phase variation of Reynolds shear stress underneath surface wave using streamline coordinates.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Paskin, Liad
Conan, Boris
Perignon, Yves
and
Aubrun, Sandrine
2022.
A Dynamic Large-Scale Driving-Force to Control the Targeted Wind Speed in Large Eddy Simulations above Ocean Waves.
Atmosphere,
Vol. 13,
Issue. 12,
p.
2012.
Ayet, Alex
and
Chapron, Bertrand
2022.
The Dynamical Coupling of Wind-Waves and Atmospheric Turbulence: A Review of Theoretical and Phenomenological Models.
Boundary-Layer Meteorology,
Vol. 183,
Issue. 1,
p.
1.
Paskin, Liad
Conan, Boris
Perignon, Yves
and
Aubrun, Sandrine
2022.
Evidence of Ocean Waves Signature in the Space–Time Turbulent Spectra of the Lower Marine Atmosphere Measured by a Scanning LiDAR.
Remote Sensing,
Vol. 14,
Issue. 13,
p.
3007.
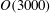 $O(3000)$ peak wave periods. Using the numerical result, we compute the universal constant in a wave-growth law proposed in the literature, and substantiate the scaling of wind–wave growth based on intrinsic wave properties.
$O(3000)$ peak wave periods. Using the numerical result, we compute the universal constant in a wave-growth law proposed in the literature, and substantiate the scaling of wind–wave growth based on intrinsic wave properties.


