Article contents
Spilling breakers in shallow water: applications to Favre waves and to the shoaling and breaking of solitary waves
Published online by Cambridge University Press: 02 November 2016
Abstract
A two-layer long-wave approximation of the homogeneous Euler equations for a free-surface flow evolving over mild slopes is derived. The upper layer is turbulent and is described by depth-averaged equations for the layer thickness, average fluid velocity and fluid turbulent energy. The lower layer is almost potential and can be described by Serre–Su–Gardner–Green–Naghdi equations (a second-order shallow water approximation with respect to the parameter 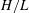 $H/L$, where
$H/L$, where 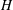 $H$ is a characteristic water depth and
$H$ is a characteristic water depth and 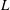 $L$ is a characteristic wavelength). A simple model for vertical turbulent mixing is proposed governing the interaction between these layers. Stationary supercritical solutions to this model are first constructed, containing, in particular, a local turbulent subcritical zone at the forward slope of the wave. The non-stationary model was then numerically solved and compared with experimental data for the following two problems. The first one is the study of surface waves resulting from the interaction of a uniform free-surface flow with an immobile wall (the water hammer problem with a free surface). These waves are sometimes called ‘Favre waves’ in homage to Henry Favre and his contribution to the study of this phenomenon. When the Froude number is between 1 and approximately 1.3, an undular bore appears. The characteristics of the leading wave in an undular bore are in good agreement with experimental data by Favre (Ondes de Translation dans les Canaux Découverts, 1935, Dunod) and Treske (J. Hydraul Res., vol. 32 (3), 1994, pp. 355–370). When the Froude number is between 1.3 and 1.4, the transition from an undular bore to a breaking (monotone) bore occurs. The shoaling and breaking of a solitary wave propagating in a long channel (300 m) of mild slope (1/60) was then studied. Good agreement with experimental data by Hsiao et al. (Coast. Engng, vol. 55, 2008, pp. 975–988) for the wave profile evolution was found.
$L$ is a characteristic wavelength). A simple model for vertical turbulent mixing is proposed governing the interaction between these layers. Stationary supercritical solutions to this model are first constructed, containing, in particular, a local turbulent subcritical zone at the forward slope of the wave. The non-stationary model was then numerically solved and compared with experimental data for the following two problems. The first one is the study of surface waves resulting from the interaction of a uniform free-surface flow with an immobile wall (the water hammer problem with a free surface). These waves are sometimes called ‘Favre waves’ in homage to Henry Favre and his contribution to the study of this phenomenon. When the Froude number is between 1 and approximately 1.3, an undular bore appears. The characteristics of the leading wave in an undular bore are in good agreement with experimental data by Favre (Ondes de Translation dans les Canaux Découverts, 1935, Dunod) and Treske (J. Hydraul Res., vol. 32 (3), 1994, pp. 355–370). When the Froude number is between 1.3 and 1.4, the transition from an undular bore to a breaking (monotone) bore occurs. The shoaling and breaking of a solitary wave propagating in a long channel (300 m) of mild slope (1/60) was then studied. Good agreement with experimental data by Hsiao et al. (Coast. Engng, vol. 55, 2008, pp. 975–988) for the wave profile evolution was found.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 35
- Cited by



