Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ostilla-Mónico, Rodolfo
van der Poel, Erwin P.
Verzicco, Roberto
Grossmann, Siegfried
and
Lohse, Detlef
2014.
Exploring the phase diagram of fully turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 761,
Issue. ,
p.
1.
Chouippe, A.
Climent, E.
Legendre, D.
and
Gabillet, C.
2014.
Numerical simulation of bubble dispersion in turbulent Taylor-Couette flow.
Physics of Fluids,
Vol. 26,
Issue. 4,
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
and
Lohse, Detlef
2015.
Effects of the computational domain size on direct numerical simulations of Taylor-Couette turbulence with stationary outer cylinder.
Physics of Fluids,
Vol. 27,
Issue. 2,
Huisman, Sander G.
van der Veen, Roeland C. A.
Bruggert, Gert-Wim H.
Lohse, Detlef
and
Sun, Chao
2015.
The boiling Twente Taylor-Couette (BTTC) facility: Temperature controlled turbulent flow between independently rotating, coaxial cylinders.
Review of Scientific Instruments,
Vol. 86,
Issue. 6,
Fokoua, G. Ndongo
Gabillet, C.
Aubert, A.
and
Colin, C.
2015.
Effect of bubble’s arrangement on the viscous torque in bubbly Taylor-Couette flow.
Physics of Fluids,
Vol. 27,
Issue. 3,
Singh, Harminder
Suazo, Claudio Alberto Torres
and
Liné, Alain
2016.
Log law of the wall revisited in Taylor-Couette flows at intermediate Reynolds numbers.
Physical Review E,
Vol. 94,
Issue. 5,
Spandan, Vamsi
Ostilla-Monico, Rodolfo
Lohse, Detlef
and
Verzicco, Roberto
2016.
Identifying coherent structures and vortex clusters in Taylor-Couette turbulence.
Journal of Physics: Conference Series,
Vol. 708,
Issue. ,
p.
012006.
Campagne, Antoine
Machicoane, Nathanaël
Gallet, Basile
Cortet, Pierre-Philippe
and
Moisy, Frédéric
2016.
Turbulent drag in a rotating frame.
Journal of Fluid Mechanics,
Vol. 794,
Issue. ,
Grossmann, Siegfried
Lohse, Detlef
and
Sun, Chao
2016.
High–Reynolds Number Taylor-Couette Turbulence.
Annual Review of Fluid Mechanics,
Vol. 48,
Issue. 1,
p.
53.
Spandan, Vamsi
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
and
Lohse, Detlef
2016.
Drag reduction in numerical two-phase Taylor–Couette turbulence using an Euler–Lagrange approach.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
411.
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
Grossmann, Siegfried
and
Lohse, Detlef
2016.
The near-wall region of highly turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
95.
Brauckmann, Hannes J.
Salewski, Matthew
and
Eckhardt, Bruno
2016.
Momentum transport in Taylor–Couette flow with vanishing curvature.
Journal of Fluid Mechanics,
Vol. 790,
Issue. ,
p.
419.
van der Veen, Roeland C. A.
Huisman, Sander G.
Merbold, Sebastian
Harlander, Uwe
Egbers, Christoph
Lohse, Detlef
and
Sun, Chao
2016.
Taylor–Couette turbulence at radius ratio : scaling, flow structures and plumes.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
p.
334.
Spandan, Vamsi
Lohse, Detlef
and
Verzicco, Roberto
2016.
Deformation and orientation statistics of neutrally buoyant sub-Kolmogorov ellipsoidal droplets in turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 809,
Issue. ,
p.
480.
Brauckmann, Hannes J.
and
Eckhardt, Bruno
2017.
Marginally stable and turbulent boundary layers in low-curvature Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 815,
Issue. ,
p.
149.
Froitzheim, A.
Merbold, S.
and
Egbers, C.
2017.
Velocity profiles, flow structures and scalings in a wide-gap turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
330.
Jalalabadi, Razieh
Kim, Jongmin
and
Sung, Hyung Jin
2017.
Turbulent structures in an optimal Taylor–Couette flow between concentric counter-rotating cylinders.
Journal of Turbulence,
Vol. 18,
Issue. 5,
p.
480.
Ostilla-Mónico, Rodolfo
Zhu, Xiaojue
Spandan, Vamsi
Verzicco, Roberto
and
Lohse, Detlef
2017.
Life stages of wall-bounded decay of Taylor-Couette turbulence.
Physical Review Fluids,
Vol. 2,
Issue. 11,
Zhu, Bihai
Ji, Zengqi
Lou, Zhengkun
and
Qian, Pengcheng
2018.
Torque scaling in small-gap Taylor-Couette flow with smooth or grooved wall.
Physical Review E,
Vol. 97,
Issue. 3,
Ding, Zijing
and
Marensi, Elena
2019.
Upper bound on angular momentum transport in Taylor-Couette flow.
Physical Review E,
Vol. 100,
Issue. 6,
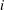 $i$) and outer (
$i$) and outer ( $o$) cylinders is explored numerically and experimentally to determine the effects of the radius ratio
$o$) cylinders is explored numerically and experimentally to determine the effects of the radius ratio 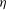 $\eta $ on the system response. Numerical simulations reach Reynolds numbers of up to
$\eta $ on the system response. Numerical simulations reach Reynolds numbers of up to 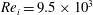 $\mathit{Re}_i=9.5\times 10^3$ and
$\mathit{Re}_i=9.5\times 10^3$ and 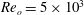 $\mathit{Re}_o=5\times 10^3$, corresponding to Taylor numbers of up to
$\mathit{Re}_o=5\times 10^3$, corresponding to Taylor numbers of up to 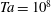 $\mathit{Ta}=10^8$ for four different radius ratios
$\mathit{Ta}=10^8$ for four different radius ratios 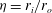 $\eta =r_i/r_o$ between 0.5 and 0.909. The experiments, performed in the Twente Turbulent Taylor–Couette (
$\eta =r_i/r_o$ between 0.5 and 0.909. The experiments, performed in the Twente Turbulent Taylor–Couette (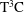 $\mathrm{T^3C}$) set-up, reach Reynolds numbers of up to
$\mathrm{T^3C}$) set-up, reach Reynolds numbers of up to 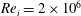 $\mathit{Re}_i=2\times 10^6$ and
$\mathit{Re}_i=2\times 10^6$ and 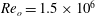 $\mathit{Re}_o=1.5\times 10^6$, corresponding to
$\mathit{Re}_o=1.5\times 10^6$, corresponding to 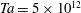 $\mathit{Ta}=5\times 10^{12}$ for
$\mathit{Ta}=5\times 10^{12}$ for 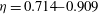 $\eta =0.714\mbox{--}0.909$. Effective scaling laws for the torque
$\eta =0.714\mbox{--}0.909$. Effective scaling laws for the torque 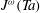 $J^{\omega }(\mathit{Ta})$ are found, which for sufficiently large driving
$J^{\omega }(\mathit{Ta})$ are found, which for sufficiently large driving 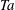 $\mathit{Ta}$ are independent of the radius ratio
$\mathit{Ta}$ are independent of the radius ratio 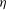 $\eta $. As previously reported for
$\eta $. As previously reported for 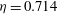 $\eta =0.714$, optimum transport at a non-zero Rossby number
$\eta =0.714$, optimum transport at a non-zero Rossby number 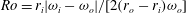 $\mathit{Ro}=r_i |\omega _i-\omega _o |/[2(r_o-r_i)\omega _o]$ is found in both experiments and numerics. Here
$\mathit{Ro}=r_i |\omega _i-\omega _o |/[2(r_o-r_i)\omega _o]$ is found in both experiments and numerics. Here 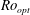 $\mathit{Ro}_{opt}$ is found to depend on the radius ratio and the driving of the system. At a driving in the range between
$\mathit{Ro}_{opt}$ is found to depend on the radius ratio and the driving of the system. At a driving in the range between 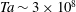 $\mathit{Ta}\sim 3\times 10^{8}$ and
$\mathit{Ta}\sim 3\times 10^{8}$ and 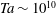 $\mathit{Ta}\sim 10^{10}$,
$\mathit{Ta}\sim 10^{10}$, 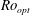 $\mathit{Ro}_{opt}$ saturates to an asymptotic
$\mathit{Ro}_{opt}$ saturates to an asymptotic 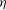 $\eta $-dependent value. Theoretical predictions for the asymptotic value of
$\eta $-dependent value. Theoretical predictions for the asymptotic value of 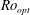 $\mathit{Ro}_{opt}$ are compared to the experimental results, and found to differ notably. Furthermore, the local angular velocity profiles from experiments and numerics are compared, and a link between a flat bulk profile and optimum transport for all radius ratios is reported.
$\mathit{Ro}_{opt}$ are compared to the experimental results, and found to differ notably. Furthermore, the local angular velocity profiles from experiments and numerics are compared, and a link between a flat bulk profile and optimum transport for all radius ratios is reported.

