Article contents
On the weakly nonlinear seakeeping solution near the critical frequency
Published online by Cambridge University Press: 11 May 2018
Abstract
We study theoretically and numerically the nonlinear seakeeping problem of a submerged or floating body translating with constant forward speed
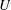 $U$
parallel to the undisturbed free surface while at the same time undergoing a small oscillatory motion and/or encountering small-amplitude waves at frequency
$U$
parallel to the undisturbed free surface while at the same time undergoing a small oscillatory motion and/or encountering small-amplitude waves at frequency
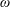 $\unicode[STIX]{x1D714}$
. It is known that at the critical frequency corresponding to
$\unicode[STIX]{x1D714}$
. It is known that at the critical frequency corresponding to
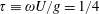 $\unicode[STIX]{x1D70F}\equiv \unicode[STIX]{x1D714}U/g=1/4$
, where
$\unicode[STIX]{x1D70F}\equiv \unicode[STIX]{x1D714}U/g=1/4$
, where
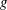 $g$
is the gravitational acceleration, the classical linear solution is unbounded for a single point source, and the inclusion of third-order free-surface nonlinearity due to cubic self-interactions of waves is necessary to remove the associated singularity. Although it has been shown that the linear solution is in fact bounded for a body with full geometry rather than a point source, the solution still varies sharply near the critical frequency. In this work, we show theoretically that for a submerged body, the nonlinear correction to the linear solution due to cubic self-interactions of resonant waves in the neighbourhood of
$g$
is the gravitational acceleration, the classical linear solution is unbounded for a single point source, and the inclusion of third-order free-surface nonlinearity due to cubic self-interactions of waves is necessary to remove the associated singularity. Although it has been shown that the linear solution is in fact bounded for a body with full geometry rather than a point source, the solution still varies sharply near the critical frequency. In this work, we show theoretically that for a submerged body, the nonlinear correction to the linear solution due to cubic self-interactions of resonant waves in the neighbourhood of
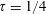 $\unicode[STIX]{x1D70F}=1/4$
is of first order in the wave steepness (or body motion amplitude), which is the same order as the linear solution. With the inclusion of nonlinear effects in the dispersion relation, the wavenumbers of resonant waves become complex-valued and the resonant waves become evanescent, with their amplitudes vanishing with the distance away from the body. To assist in understanding the theory, we derive the analytic nonlinear solution for the case of a submerged two-dimensional circular cylinder in the neighbourhood of
$\unicode[STIX]{x1D70F}=1/4$
is of first order in the wave steepness (or body motion amplitude), which is the same order as the linear solution. With the inclusion of nonlinear effects in the dispersion relation, the wavenumbers of resonant waves become complex-valued and the resonant waves become evanescent, with their amplitudes vanishing with the distance away from the body. To assist in understanding the theory, we derive the analytic nonlinear solution for the case of a submerged two-dimensional circular cylinder in the neighbourhood of
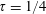 $\unicode[STIX]{x1D70F}=1/4$
. Independent numerical simulations confirm the analytic solution for the submerged circular cylinder. Finally, we also demonstrate by numerical simulations that similar significant nonlinear effects for a surface-piercing body exist in the neighbourhood of
$\unicode[STIX]{x1D70F}=1/4$
. Independent numerical simulations confirm the analytic solution for the submerged circular cylinder. Finally, we also demonstrate by numerical simulations that similar significant nonlinear effects for a surface-piercing body exist in the neighbourhood of
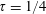 $\unicode[STIX]{x1D70F}=1/4$
.
$\unicode[STIX]{x1D70F}=1/4$
.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 8
- Cited by



