Article contents
Numerical study of extreme mechanical force exerted by a turbulent flow on a bluff body by direct and rare-event sampling techniques
Published online by Cambridge University Press: 18 May 2020
Abstract
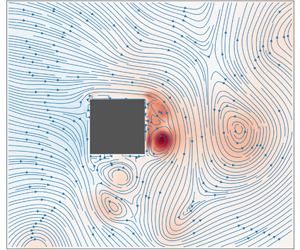
This study investigates, by means of numerical simulations, extreme mechanical force exerted by a turbulent flow impinging on a bluff body, and examines the relevance of two distinct rare-event algorithms to efficiently sample these events. The drag experienced by a square obstacle placed in a turbulent channel flow (in two dimensions) is taken as a representative case study. Direct sampling shows that extreme fluctuations are closely related to the presence of a strong vortex blocked in the near wake of the obstacle. This vortex is responsible for a significant pressure drop between the forebody and the base of the obstacle, thus yielding a very high value of the drag. Two algorithms are then considered to speed up the sampling of such flow scenarios, namely the adaptive multilevel splitting (AMS) and the Giardina–Kurchan–Tailleur–Lecomte (GKTL) algorithms. The general idea behind these algorithms is to replace a long simulation by a set of much shorter ones, running in parallel, with dynamics that is replicated or pruned, according to some specific rules designed to sample large-amplitude events more frequently. These algorithms have been shown to be relevant for a wide range of problems in statistical physics, computer science, biochemistry. The present study is the first application to a fluid–structure interaction problem. Practical evidence is given that the fast sweeping time of turbulent fluid structures past the obstacle has a strong influence on the efficiency of the rare-event algorithm. While the AMS algorithm does not yield significant run-time savings as compared to direct sampling, the GKTL algorithm appears to be effective in sampling very efficiently extreme fluctuations of the time-averaged drag and estimating related statistics such as return times. Software used for simulations and data processing is available at https://github.com/tlestang/paper_extreme_drag_fluctuations.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 12
- Cited by


