Article contents
New oscillatory instability of a confined cylinder in a flow below the vortex shedding threshold
Published online by Cambridge University Press: 24 November 2011
Abstract
A new type of flow-induced oscillation is reported for a tethered cylinder confined inside a Hele-Shaw cell (ratio of cylinder diameter to cell aperture, 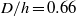 ) with its main axis perpendicular to the flow. This instability is studied numerically and experimentally as a function of the Reynolds number
) with its main axis perpendicular to the flow. This instability is studied numerically and experimentally as a function of the Reynolds number 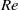 and of the density
and of the density 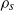 of the cylinder. This confinement-induced vibration (CIV) occurs above a critical Reynolds number
of the cylinder. This confinement-induced vibration (CIV) occurs above a critical Reynolds number 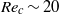 much lower than for Bénard–Von Kármán vortex shedding behind a fixed cylinder in the same configuration (
much lower than for Bénard–Von Kármán vortex shedding behind a fixed cylinder in the same configuration (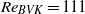 ). For low
). For low 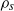 values, CIV persists up to the highest
values, CIV persists up to the highest 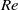 value investigated (
value investigated (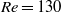 ). For denser cylinders, these oscillations end abruptly above a second value of
). For denser cylinders, these oscillations end abruptly above a second value of 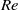 larger than
larger than 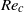 and vortex-induced vibrations (VIV) of lower amplitude appear for
and vortex-induced vibrations (VIV) of lower amplitude appear for 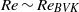 . Close to the first threshold
. Close to the first threshold 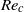 , the oscillation amplitude variation as
, the oscillation amplitude variation as 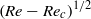 and the lack of hysteresis demonstrate that the process is a supercritical Hopf bifurcation. Using forced oscillations, the transverse position of the cylinder is shown to satisfy a Van der Pol equation. The physical meaning of the stiffness, amplification and total mass coefficients of this equation are discussed from the variations of the pressure field.
and the lack of hysteresis demonstrate that the process is a supercritical Hopf bifurcation. Using forced oscillations, the transverse position of the cylinder is shown to satisfy a Van der Pol equation. The physical meaning of the stiffness, amplification and total mass coefficients of this equation are discussed from the variations of the pressure field.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 11
- Cited by


